周秋月,吴晓东,梁钰,谢坚锋,吴顺,邹磊

(江苏大学材料科学与工程学院,镇江２１２０１３)

摘　要:采用热模拟试验机对６０Si２CrVAT 高强度弹簧钢在不同温度(９００,９５０,１０５０,１１５０℃)和应变速率下(０．１,１,５,１０s－１)进行热压缩变形,研究了变形温度和应变速率对该钢热变形行为的影响规律;在此基础上,根据Arrhenius双曲正弦方程,建立了该钢的热压缩变形本构方程.结果表明:该钢的流变应力随着变形速率的增大而增大,随变形温度的升高而减小,动态再结晶在高变形温度和低应变速率下更容易发生;真应变为０．２时的变形激活能为３７２kJ??mol－１,流变应力的计算值与试验值之间的平均相对误差为４．８９％,吻合得较好.

关键词:弹簧钢;热压缩变形;流变应力;本构方程

中图分类号:TG３３５文献标志码:A文章编号:１０００Ｇ３７３８(２０１７)０４Ｇ００２９Ｇ０４

０　引　言

６０Si２CrVAT高强度弹簧钢具有良好的综合性能,主要用于制造高载荷、耐冲击弹簧,如铁路货车转向架旁承弹簧和汽车悬架弹簧等.随着我国铁路列车的提速,为了保证货车的稳定与安全,对弹簧钢的性能要求也随之提高,主要表现在需要其具备较高的力学性能、抗弹减性能、疲劳性能以及物理化学性能等[１].本构关系可以表征材料的流变应力与变

形温度、应变速率以及真应变等参数之间的关系,因而是金属塑性加工领域有限元数值模拟技术的前提条件,也是金属塑性加工工艺设计的基础[２].据所查资料显示,前人对６０Si２CrVAT 弹簧钢流变应力的研究甚少,因此作者采用GleebleＧ３８００型热模拟试验机对该钢在不同条件下进行热压缩变形,研究了变形温度和应变速率对其流变应力的影响,并建立了该钢的本构方程,为科学合理地制定该钢的轧制工艺提供参考[３－４].

１　试样制备与试验方法

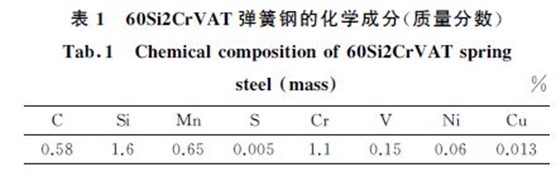
试验用６０Si２CrVAT 弹簧钢预锻毛坯由淮钢提供,其化学成分如表１所示,在其上加工出尺寸为?８mm×１２mm 的压缩试样.

在GleebleＧ３８００型热模拟试验机上将试样以１０℃??s－１的加热速率从室温加热到１２００ ℃,保温３min后再以１０ ℃??s－１ 的冷却速率分别冷却至１１５０,１０５０,９５０,９００ ℃,保温３０s;然后再以不同的应变速率(０．１,１,５,１０s－１)进行单道次压缩变形,变形量为５６％,压缩变形完成后迅速进行水淬.

２　试验结果与讨论

２．１　真应力Ｇ真应变曲线

由图１可以看出,在相同的应变速率下,变形温度越高,应力值越低.这是因为随着变形温度升高,

原子运动加剧,动能增大,原子之间的结合力减弱,流变应力降低.在应变速率为０．１s－１和１s－１、变形温度为１０５０ ℃和１１５０ ℃时,流变应力首先随真应变的增加而迅速上升,达到峰值后逐渐下降,之后随着变形的进行,加工硬化加剧,动态回复和软化比较困难,流变应力继续上升,真应力Ｇ真应变曲线为动态再结晶型.在应变速率为５s－１和１０s－１时,真应力先随应变的增加而迅速增大,超过一定应变量后,真应力基本保持在一个定值,即呈现出稳态的流变特征,真应力Ｇ真应变曲线为动态回复型.这是由于软化需要一个时间过程,当应变速率较大时,位错增殖速度加快,出现位错缠结,阻碍了位错运动,晶粒没有足够的时间长大;当应变速率较小时,晶粒有足够的时间形核长大,即容易发生动再结晶.由图１(a)和(b)可以看出,在较高的变形温度(１０５０,１１５０ ℃)下,真应力Ｇ真应变曲线的峰比较明显,这是由于温度越高,晶粒长大的驱动力就越大,越容易发生动态再结晶.

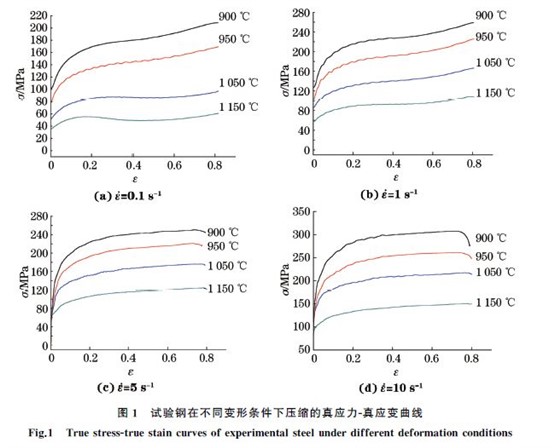
由图１还可以看出,在低的应变速率(０．１s－１)下,真应力Ｇ真应变曲线在出现一个峰值后出现了非常明显的动态软化,而在较高的应变速率(５,１０s－１)下,流变应力先上升,到达一定值后呈相对稳定的状态. 这是由于应变速率较大,再结晶所需驱动力增加,而累积的位错能较低,未达到动再结晶发生的条件,此时主要的软化机制为动态回复,当加工硬化与动态回复达到平衡时,流变应力趋向一个稳定值.

２．２　本构方程的建立

在高温塑性变形条件下,流变应力、应变速率以及变形温度这些变形参数之间的关系可用Sellars和Tegart通过试验研究提出的Arrhenius方程表示[５－８]:

式中:A ,n１,α 和β 为常数;ε?? 为应变速率;R 为气体常数;T 为热力学温度;Q 为变形激活能;σ 为真应力;α＝β/n１.

从式(４)所示的Arrhenius型双曲正弦方程可以看出,只要确定了不同应变下参数Q,A ,n 和α 的值,就可以确定材料在任意变形条件下的流变应力.由图１可以看出,６０Si２CrVAT弹簧钢的流变应力随着真应变的增加是变化的,因而Q,A ,n,α 等参数应该是真应变的函数,因此在求流变应力σ 时,应先确定出不同真应变下Q,A ,n,α 的值.现以ε＝０．２为例来说明求解过程,其余每隔０．０２取点计算. 材料在高温塑性变形时,应变速率受热激活过程的控制,应变速率与温度之间的关系可用温度补偿的应变速率因子ZenerＧHollomon参数(Z 参数)表示[９]:

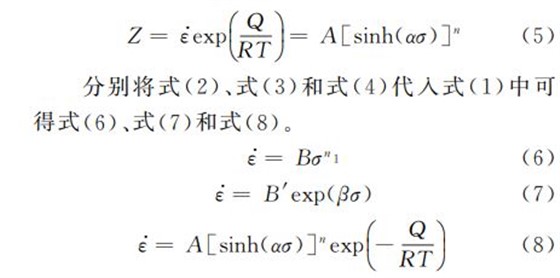
式中:B 和B′为与温度无关的常数.对式(６)和式(７)两边取对数,可知lnε??Ｇσ 和lnε??Ｇlnσ 都呈线性关系,带入试验数据作图,结果如图２,３ 所示,进行线性拟合得出斜率,并求平均值,得n１ ＝８．２５１,β＝０．０５３６,由此对应的α＝０．００６５.将计算所得的α 带入式(８),并对式(８)取对数,得:

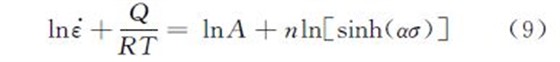
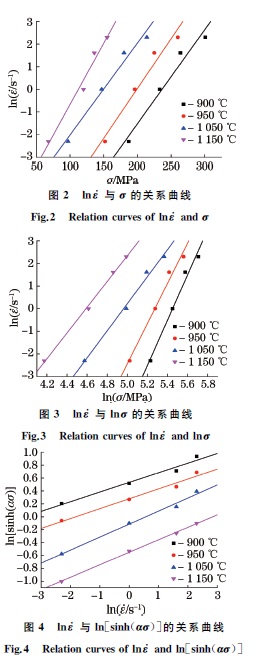
真应变为０．２时,不同变形温度和应变速率下的ln[sinh(ασ)]Ｇlnε?? 关系如图４所示,进行线性拟合后可得斜率的平均值,即n＝６．０６４３.对图５所示的ln[sinh(ασ)]Ｇ１/T 关 系 曲 线 进 行 线 性 拟 合,

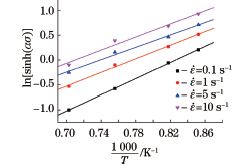
图５ ln[sinh(ασ)与１/T 的关系曲线

Fig．５ Relationcurvesof１/Tandln[sinh(ασ)]

计算得到斜 率 的 平 均 值 为 ７．３９０.由 上 述 参 数 可计算得到变形激活能 Q 为３７２kJ??mol－１.由图４

可得截距为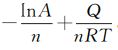,进而求得A＝５．５１×１０１４.

的热压缩变形本构方程为:

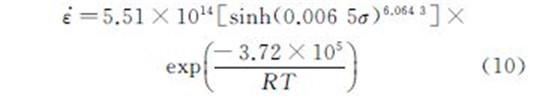
按照上述的计算过程,每隔０．０２取点,可以求出不同真应变下Q,α,n,A 等参数的值,采用多元线性回归可以确定这些参数与真应变之间的关系,见式(１１)~(１４).

将计算所得的σ,n,Q,A 等参数与真应变的关系式代入式(８)中,便可得到６０Si２CrVAT 弹簧钢在变形温度为(９００~１１５０ ℃)、变形速率为(０．１~０s－１)下的压缩变形本构方程.

２．３　本构方程的误差

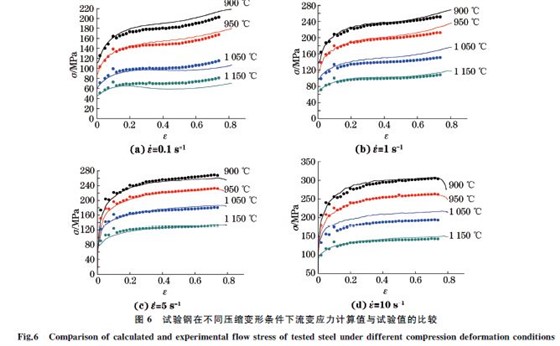
从图６可以看出,６０Si２CrVAT 弹簧钢在不同压缩变形条件下流变应力的计算值与试验值吻合得较好,它们之间的平均相对误差为４．８９％.由此说明建立的本构方程能够较精确地预测６０Si２CrVAT弹簧钢的流变应力,可为制定合理的轧制工艺提供理论依据[７,１０].

结　论

(１)６０Si２CrVAT弹簧钢的流变应力随应变速率的增大而增大,随变形温度的升高而减小;在低应变速率时,真应力Ｇ真应变曲线为动态再结晶型;在高应变速率时,真应力Ｇ应变曲线为动态回复型.

(２)在Arrhenius方程的基础上,建立了双曲正弦方程中Q,A ,n,α 等参数与真应变的函数关系式,从而构建出了包含变形温度、应变速率在内的双曲正弦方程形式的６０Si２CrVAT 弹簧钢热压缩变形本构方程.

文章来源：材料与测试网