摘 要:采用流体体积方法耦合雷诺应力模型与离散相模型结合泰勒类比不稳定性破碎模型, 利用计算流体力学软件 Fluent19.2,对紧耦合环缝喷嘴初次雾化与二次雾化进行全流程仿真,并进 行了试验验证。结果表明:初次雾化过程使导流管底部形成环形液膜结构,液膜前端的初次雾化主 要是气体射流自由边界湍流剪切的结果,并且初次雾化形成的液滴直径满足正态分布;随着分散的 液滴群外侧接触气体射流,从液滴群的外侧开始向心部发生二次雾化过程,但是未接触气体射流的 液滴仍保持较高的过热度。仿真得到紧耦合环缝喷嘴二次雾化后粉末的直径与试验结果吻合较 好,相对误差小于5%,验证了仿真的准确性。

关键词:真空感应气体雾化;紧耦合环缝喷嘴;初次雾化;二次雾化

中图分类号:TF123 文献标志码:A 文章编号:1000-3738(2022)04-0075-07

0 引 言

随着金属增材制造与粉末冶金等行业的发展, 对高质量金属粉末的需求日益增加[1]。目前主要的 金属粉末制备方法包括以德国 ALD 公司为代表的电极 感 应 熔 炼 气 体 雾 化 法 (electrodeinduction meltinggasatomization,EIGA),以加拿大为代表 的等离子雾化 (plasmaatomization,PA)工艺与等 离 子 旋 转 电 极 雾 化 (plasmarotating electrode process,PREP)工艺以及传统的真空感应气雾化 (vacuum induction gas atomization,VIGA)工 艺[2-3]。前3种工艺主要用于制备高活性金属粉末, 如钛及钛合金。对于传统的不锈钢、铝合金以及铜 合金等粉末材料主要采用 VIGA 工艺进行制备,因 此该工艺在国内外得到了广泛的应用。 气雾化喷嘴是 VIGA 设备的核心部件,决定了 制备金属粉末的直径分布、空心率、卫星粉率等关键 技术指标[4]。气雾化喷嘴主要分为紧耦合式喷嘴与 自由落体式喷嘴。紧耦合式喷嘴可大大缩短气体射 流与导流管出口金属液流的距离,显著提高雾化效 率,因此应用广泛。VIGA 工艺制粉是在一个密闭 的炉体内进行的,采用试验手段很难直接对其喷嘴 雾化进行研究。随着计算流体力学的发展,大量研 究人员开始采用流体仿真与试验验证相结合的方式 对喷嘴雾化进行研究。喷嘴雾化过程分为初次雾化 与二次雾化[5-6]。ZEOLI等[7-8]忽略金属液流的初 次雾化过程,采用欧拉-拉格朗日方法对紧耦合环缝 喷嘴的液 滴 二 次 雾 化 以 及 凝 固 过 程 进 行 了 研 究。 MOTAMAN 等[9-10]采用单相气流场仿真与纹影技 术相结合,对紧耦合式喷嘴的雾化气体流场进行了 研究。朱玲玲等[11]采用流体体积(volumeoffluid, VOF)多相流模型对紧耦合式喷嘴初次雾化过程进 行了仿真,研究了喷嘴雾化压力和液体表面张力对 金属液流初次破碎过程的影响。紧耦合式喷嘴气雾 化制粉是一个初次雾化与二次雾化连续进行的整体 过程,但是目前大部分报道都只是对其中某部分过 程进行仿真研究。

金属液流全流程雾化过程的仿真对气雾化制粉 机理的探究与喷嘴结构的优化设计都有着重要的作 用。作 者 采 用 VOF 方 法 耦 合 雷 诺 应 力 模 型 (Reynoldsstressmodel,RSM)与离散相(discrete phasemodel,DPM)模 型 结 合 泰 勒 类 比 (Taylor analogybreak-up,TAB)不稳定性破碎模型,利用 基于 有 限 体 积 方 法 的 商 业 计 算 流 体 力 学 软 件 Fluent19.2对紧耦合环缝喷嘴的 初 次 雾 化 与 二 次 雾化进行全流程仿真,并进行了试验验证,研究喷 嘴的雾化过 程,以 期 为 喷 嘴 结 构 优 化 设 计 提 供 理 论基础。

1 试验方法

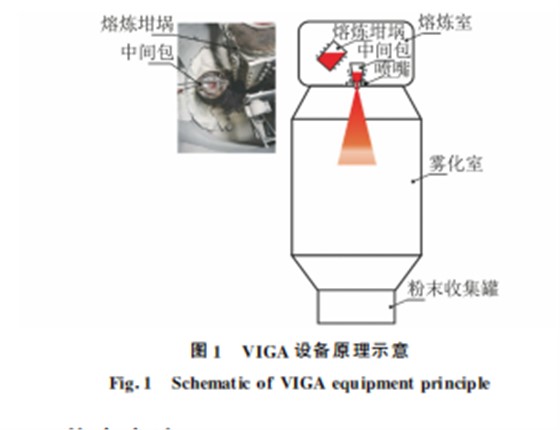
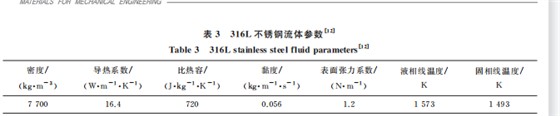
VIGA 设备原理如图1所示,该设备主要由熔 炼室、熔炼坩埚、中间包、喷嘴、雾化室、粉末收集罐 等 关 键 部 分 组 成。 熔 炼 坩 埚 最 大 熔 炼 质 量 为 100kg,最高加热温度为1973K,中间包最高保温 温度为1573K。制粉原料选择316L不锈钢,雾化 气体选择氩气。VIGA 方法制备金属粉末过程中, 熔炼室内气体压力基本稳定为25kPa,底部雾化室 内气体压力基本为-10kPa;316L 不锈钢熔炼温 度为1700K,中间包保温温度为1550K;雾化氩 气的进气压力为3.5MPa,气体温度为300K。制备 的样3,1并6利L用不激锈光钢粒粉度末仪采对用粉三末点粒取径样进获行得测3试组。

2 仿真方法

2.1 初次雾化仿真模型

紧初耦次合雾环化缝仿喷真嘴模的型初次雾化仿真采用 VOF多 相流模型耦合 RSM 湍流模型进行。在 VOF 模型 中主要通过体积分数追踪多相流之间的相界面,描 述气/液界面的体积分数方程[12]为 ρ1q ∂∂t(αqρq)+x∂i(αqρqui) ???? ????=0 (1) 式中:ρq 为q 相密度;αq 为q 相体积分数;t为时间; ui 为xi 方向速度;xi 为二维轴对称模型的x 坐标 数值。紧耦合环缝喷嘴的雾化气体马赫数一般大于 0.3,因此需要考虑气体的压缩性。在气/液两相流 雾化过程中,由可压缩的 N-S 方程控制的连续方 程、动量方程与能量方程[13]分别为 ∂ρ∂t+ ∂∂xi(ρui)=0 (2) ∂∂t(ρui)+∂x∂j(ρuiuj)=-∂∂xpi +∂τij ∂xj +ρg +Fs(3)∂t(ρT)+∂x∂i(ρujT)=∂x∂j K∂T c∂xj -ρujT +ST(4) 式中:uj 为xj 方向的速度;xj 为二维轴对称模型 的y 坐标数值;p 为压力;g 为重力加速度;τij 为雷 诺应力张量;Fs 为表面张力;T 为温度;ρg 为气体 密度;ρ为网格单元内的加权密度;K 为气体传热系 数;c为比热容;ST 为黏性耗散项。

2.2 二次雾化仿真模型

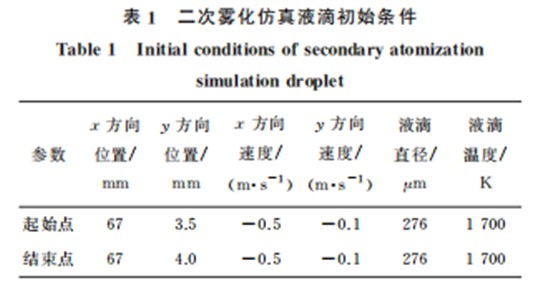
具有一定过热度的初次雾化液滴在气动力作用 下变形,在黏性力与表面张力作用下收缩发生二次 破碎过程。为了衡量液滴的二次雾化,提出了一个 重要的无量纲参数韦伯数(We),具体计算公式为 We =ρgu2reldσ (5) 式中:urel 为气体与液滴的相对速度;d 为初次雾化 液滴直径;σ为液滴表面张力系数。 韦伯数是扰动的空气动力与表面张力之比,韦 伯数越大,液滴越易破碎[14]。目前典型的液滴破碎 模型主要包括布袋式破碎、复合式破碎与脱落式破 碎[15],不同初始液滴韦伯数范围对应的破碎模型也 不同[16]。TAB模型适合描述布袋式破碎与复合式 破碎,开尔文-亥姆霍兹 KH 模型适合描述脱落式破 碎[17]。估算初次雾化液滴的韦伯数小于80,所以液 滴破碎模型为布袋式破碎、复合式破碎,因此采用 TAB模型仿真喷嘴的二次雾化过程。为了简化仿 真,将二次雾化仿真的初始液滴直径设置为初次雾 化液滴的质量中值直径。同时,利用离散相 DPM 模型,考虑液滴二次雾化过程中会出现的液滴碰撞、 液滴合并与液滴随机轨道等相关问题,选取二次雾 化仿真液滴初始条件如表1所示。

液滴在二次雾化过程中,冷却凝固转变为金属 粉末的过程是一个快速凝固的过程,液滴内部的温 度梯度与热辐射基本忽略[4]。冷却凝固过程可以采 用牛顿冷却模型进行描述[4],对应传热方程为 CpddTd dt =ΔHddfs dt - 6hρdD(Td -Tg) (6) Cpd =(1-fs)cl+csfs (7) ΔHd =ΔHf- (cl-cs)(Tl-Td) (8) h=λgD 2.0+0.6 Re 3Pr (9) 式中:Cpd 为金属液滴的恒定热容;菪Hd 为液滴的潜 热;cl 为液态的比热容;cs 为固态的比热容;ΔHf 为 单位体积金属的熔化焓;fs 为液滴中固相的体积分 数;Td 为瞬时温度;D 为二次雾化液滴直径;λg 为 雾化气体的热导率;Re 为雷诺 数;ρd 为 液 滴 的 密 度;Pr 为普朗特数;Tl 和 Tg 分别为瞬时金属液相 温度和气相温度。

2.3 网格与便捷条件

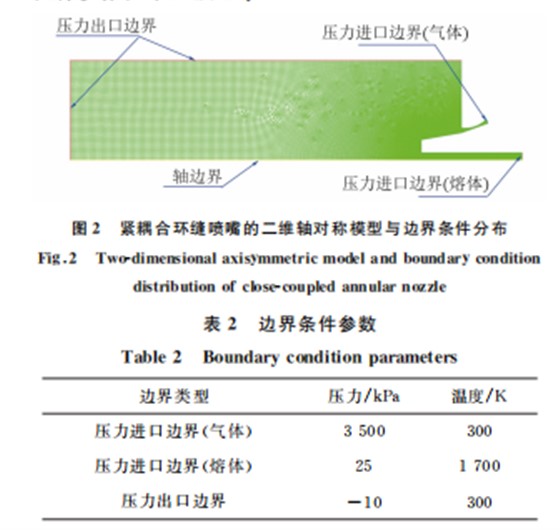
将网具格有与三边维界旋条转件对称结构的紧耦合环缝喷嘴几 何模型简 化 为 二 维 轴 对 称 结 构,对 应 几 何 模 型 如 图2所示。采用 Gambit2.4.6软件进行几何模型网 格划 分,最 小 网 格 尺 寸 为 0.1 mm,网 格 数 量 为 31691。利用 AnsysFluent19.2软件进行两相流雾 化仿真。雾化气体以一定压力进入喷嘴,将其入口 定义为压力进口边界(气体)。喷嘴顶部中间包内的 金属液流在一定气体压力作用下流入喷嘴导流管 内,因此将金属液流入口定义为压力进口边界(熔 体)。上边界与左边界为实际雾化炉体内空间位置, 设置为压力出口边界。底部边界定义为轴边界。其 他位置为喷嘴内壁面,定义为壁面边界。仿真设置 的各种边界具体压力与温度参数如表2所示。选择 氩气作为雾化气体,316L 不锈钢为制粉原料,对应 流体参数如表3所示。

采用瞬态耦合算法进行仿真,密度、动量、能量 等采用一节迎风格式进行空间离散,体积分数采用 压缩格式进行离散。初次雾化仿真时间步长为2× 10-7s,最大迭代次数为20;二次雾化仿真时间步长 为6×10-7s,最大迭代次数为20。图3为仿真模型 在不同网格数目下的初次雾化与二次雾化固定点 (x=65,y=4)位置的气体速度,当网格数目增加 至31691后,仿真的初次雾化与二次雾化在固定点 位置的气体速度基本保持为456,432m·s-1,因此 雾化仿真中采用的网格数目31691是合理的 。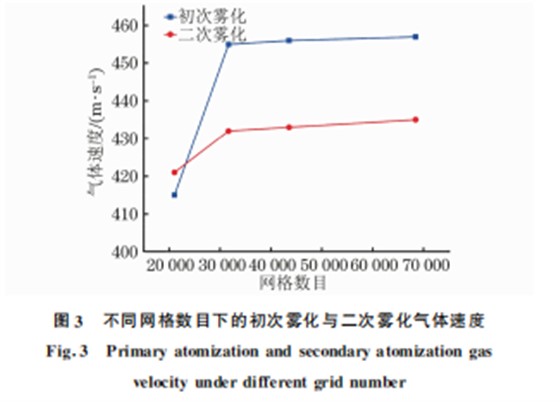

3 结果与讨论

3.1 初次雾化过程

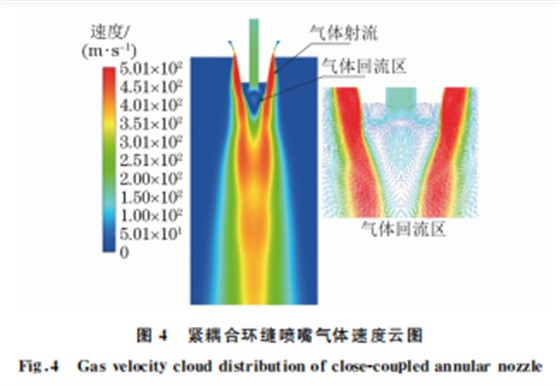
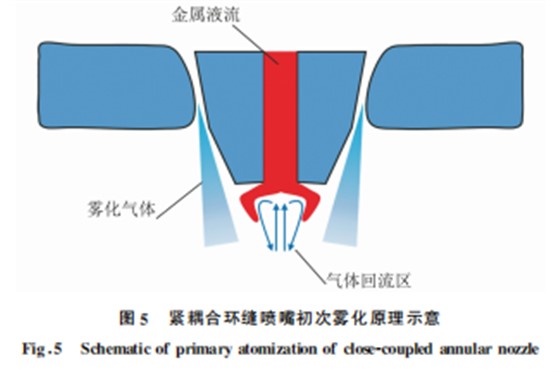
由图4可知,紧耦合环缝喷嘴出口的气体射流 主要由具有较高速度的核心区与低速的自由边界组 成。喷嘴出口位置的气流射流由于与环境压力差的 作用,导致高速气流向下喷射过程中出现压缩波与 膨胀波交替的链状结构[5]。另外,气体射流向喷嘴 底部中间位置汇聚过程中,由于气流逐渐向中间偏 转,造成在导流管底部形成了一个气体回流区。回流 区内的气体流动轨迹主要是,中间气流向上进入气体 回流区,流动一定距离后转变流动方向,逐渐沿着径 向方向流动,最终接触高速气体射流,与其一同回到 起点位置。经过气体回流区的部分气体射流,将与主 射流发生融合,形成一致向下流动的射流结构。 金属液流从导流管底部流出,接触到气体回流区后,其向下的继续流动将受到阻碍;此时金属液流 只能沿着不受阻力的径向方向继续流动,形成环形 液膜结构,实现连续液流至液膜的转变过程,如图 所示。液膜流动过程中受到气体回流区的气流拖拽5 挤压,前端的液膜厚度逐渐变薄。当径向流动的环 形液膜靠近雾化气体射流后,在气体射流拽力作用 下,再次改变流动方向,并且前端液膜将直接发生破 碎或厚度进一步减薄,最终完成初次雾化过程。

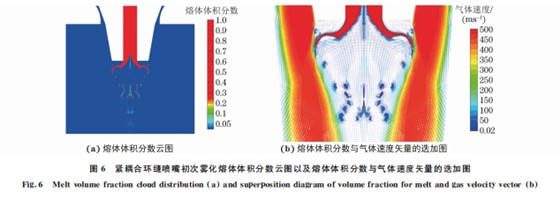
由图6可以看出:紧耦合环缝喷嘴环形液膜前 端在气体射流拖拽作用下改变了流动方向,并直接 发生了液膜的破碎,形成了一定数量的初次雾化液 滴,液滴在气体射流的作用下,逐渐向喷嘴底部中心 位置汇聚;环形液膜前端仅接触了气体射流外侧的 自由边界,液膜前端在射流边界的湍流剪切力作用 下发生破碎,形成初次雾化液滴,同时在破碎液滴下 落 过 程 中,将 在 液 滴 周 围 形 成 漩 涡 绕 流 结 构。 üNAL等[18]采用高速摄像技术研究了 VIGA 方法 中氩气雾化压力为2.4 MPa时,金属铝液的初次雾 化过程,发现铝液在导流管底部形成了一个环形液 膜结构,与仿真结果相似,基本可以验证初次雾化仿 真的可靠度。

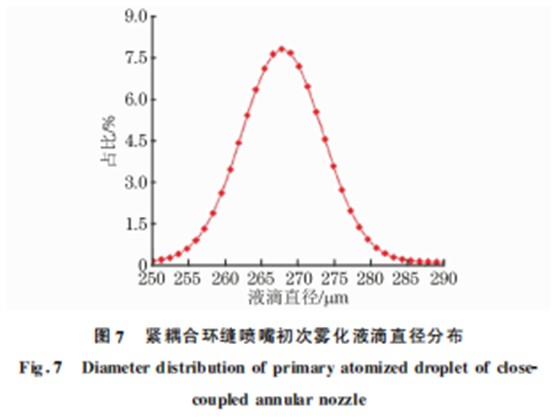
基于德洛奈三角形方法,采用 MATLAB 软件 编写计算程序,对初次雾化形成的液滴进行等效面 积直径的计算,结果如图7所示。由图7可以看出, 紧耦合环缝喷嘴初次雾化后形成的液滴直径基本符 合正态分布,主要分布在250~285μm 之间,中值 直径为268μm。综上可知,紧耦合环缝喷嘴初次雾 化的关键是环形液膜的形成,前端液膜的破碎主要 是气体射流的自由边界湍流剪切造成的,并且初次 雾化形成的液滴直径满足正态分布。

3.2 二次雾化过程

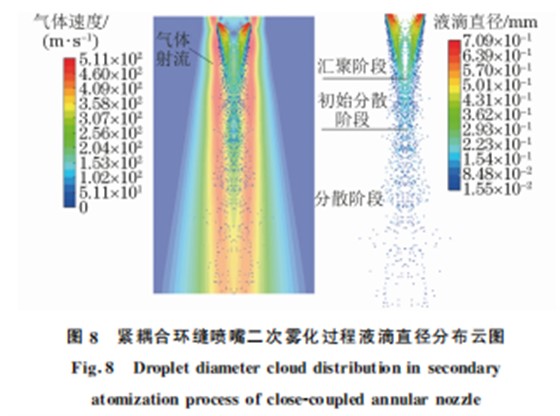
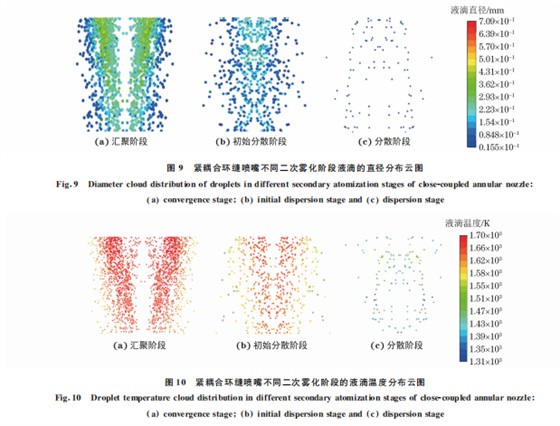
由图8可以看出,紧耦合环缝喷嘴初次雾化后 向下释放的液滴发生先汇聚后分散的变化过程,包 括液滴群汇聚阶段、初始分散阶段与分散阶段,这与 WANG 等[4]的研究结论一致。气体回流区以下发 生融合的气体射流,在连续下落的二次雾化液滴的 负载作用下,中间轴线位置的高速射流区域在径向 方向上存在一定程度的偏转。下落的雾化液滴在初 始汇聚阶段主要是液滴群的外边缘接触气体射流边 界,因此液滴的二次破碎开始主要发生在下落液滴 的外侧,如图9(a)所示。随着液滴的继续下落,流 动轨迹逐渐从汇聚阶段转变为初始分散阶段,比较 靠近中心位置且未接触气体射流的液滴也慢慢向径 向方向延伸,开始与气体射流发生作用,因此液滴群 外侧发生二次雾化的液滴数量逐渐增加,如图9(b) 所示。随着二次雾化液滴沿径向分散,喷嘴底部中 心轴线位置附近的气体射流粒子负载作用降低,射 流的径向偏转也基本消失,此时分布在液滴群中心 位置未发生二次雾化的分散阶段液滴,在继续下落 过程中直接与射流的高速核心区域作用,全部发生 雾化破碎,如图9(c)所示。

雾化气体射流的流动遵循一维流理论,即气体 速度增加的同时,温度将会发生降低[4]。液滴能进 行二次雾化的基本条件是未完成凝固过程,并且具 备一定的过热度。由图10可以看出:在液滴二次雾 化汇聚阶段,只有液滴群的外边缘接触气体射流,因 此中 心 部 位 的 液 滴 将 保 持 较 高 的 温 度 (高 于 1573K),具备进行二次雾化破碎的过热度;随着液 滴流动轨迹转变为初始分散阶段,接触低温气体射 流的液滴将逐渐增加,此时只有喷嘴底部中心轴线 位置附近的液滴还未与低温气体射流接触,保持一定过热度(液滴温度高于1573K),其他位置液滴 温度都已经接近或低于固相线温度;在分散阶段,心 部位置液滴在继续下落过程中,与低温的雾化气体 射流发生相互作用,使得剩余液滴发生二次雾化过 程而造成其过热度降低(液滴温度低于1493K), 此时所有的液滴已经凝固,二次雾化基本完成,这也 验证了实际金属液流雾化只发生在喷嘴底部很小区 域内这一结论[4]。

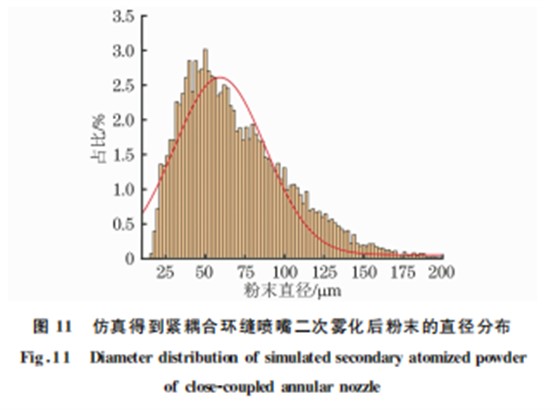
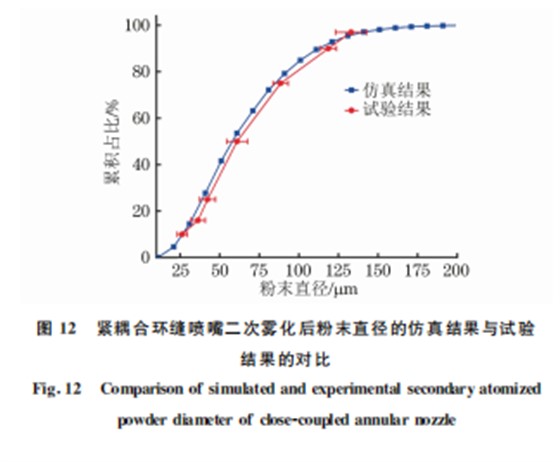
对仿真模型出口边界位置的二次雾化后的粉末 颗粒直径进行统计,结果如图11所示。由图11可 以看出,仿真得到二次雾化后粉末的直径主要分布 在15~190μm 之间,中值直径为60μm。为了验证 仿 真结果的正确性,采用与仿真相同的工艺条件与喷嘴结构,制备316L不锈钢粉末。由图12可以看 出:仿真得到紧耦合环缝喷嘴二次雾化后粉末的直 径与试验结果吻合较好,相对误差小于5%,验证了 仿真的准确性。

4 结 论

(1)紧耦合环缝喷嘴初次雾化过程将在导流管 底部形成环形液膜结构,实现连续液流至液膜的转 变过程是初次雾化的关键。液膜尖端的破碎主要是 气体射流自由边界湍流剪切的结果,并且初次雾化 液滴直径满足正态分布。

(2)紧耦合环缝喷嘴二次雾化过程分为汇聚、 初始分散与分散等3个阶段。随着液滴群外侧逐渐 靠近气体射流,液滴开始发生二次雾化过程,但是开 始未接触气体射流区域的心部液滴将保持较高的过 热度等待二次雾化。仿真得到紧耦合环缝喷嘴二次 雾化后粉末的直径与试验结果吻合较好,相对误差 小于5%,验证了仿真的准确性。

参考文献: [1] LI X G,ZHU Q,SHU S,et al.Fine spherical powder productionduringgasatomizationofpressurizedmeltsthrough melt nozzles with a small inner diameter [J].Powder Technology,2019,356:759-768. [2] 黎兴刚,刘畅,朱强.面向金属增材制造的气体雾化制粉技术研 究进展[J].航空制造技术,2019,62(22):22-34. LIXG,LIUC,ZHU Q.Researchprogressongasatomization technologyforpreparationoffeedstockpowderusedin metal additive manufacturing [J].Aeronautical Manufacturing [ Technology,2019,62(22):22-34. 3] KASSYM K,PERVEEN A.Atomizationprocessesof metal powdersfor3D printing[J].Materials Today:Proceedings, 2020,26:1727-1733. [4] WANG P,LI J,WANG X,et al.Close-coupled nozzle atomizationintegralsimulationandpowderpreparationusing vacuum induction gas atomization technology[J].Chinese PhysicsB,2021,30(2):027502. [5] 夏敏,汪鹏,张晓虎,等.电极感应熔化气雾化制粉技术中非限 制式喷嘴雾化过程模拟[J].物理学报,2018,67(17):41-51. XIA M,WANG P,ZHANG X H,etal.Computationalfluid dynamic investigation of the primary and secondary atomizationofthefree-fallatomizerin electrodeinduction meltinggasatomizationprocess[J].ActaPhysicaSinica,2018, 67(17):41-51. [6] 夏敏,汪鹏,张晓虎,等.电极感应熔化气雾化法制备高温合金 粉末中非 限 制 式 喷 嘴 的 结 构 优 化 设 计 [J].粉 末 冶 金 技 术, 2019,37(4):288-297. XIA M,WANG P,ZHANG X H,etal.Optimum structure designoffree-fallnozzleinpreparationprocessofsuperalloy powdersbyelectrodeinductiongasatomizationtechnology[J]. PowderMetallurgyTechnology,2019,37(4):288-297. [7] ZEOLIN,GU S.Computationalsimulationofmetaldroplet break-up,coolingandsolidificationduringgasatomisation[J]. ComputationalMaterialsScience,2008,43(2):268-278. [8] ZEOLIN,GUS.Numericalmodellingofdropletbreak-upfor gasatomisation[J].ComputationalMaterialsScience,2006,38 (2):282-292. [9] MOTAMAN S,MULLIS A M,COCHRANE R F,etal. Numericalandexperimentalinvestigationsoftheeffectofmelt deliverynozzledesignontheopen-toclosed-waketransitionin closed-coupledgasatomization[J].MetallurgicalandMaterials TransactionsB,2015,46(4):1990-2004. [10] MOTAMAN S,MULLIS A M,COCHRANE R F,etal. Numericalandexperimentalmodellingofbackstreamflow during close-coupled gas atomization [J].Computers & Fluids,2013,88:1-10. [11] 朱玲玲,吴建军,刘明翔,等.基于 CFD 技术的超音速喷嘴两 相流破碎机制研究[J].粉末冶金材料科学与工程,2018,23 (3):229-237. ZHULL,WUJJ,LIU M X,etal.Acomputationalfluid dynamics(CFD)researchontheatomization mechanism of two-phaseflowsin ultrasonicgasatomizer[J].Materials ScienceandEngineeringofPowderMetallurgy,2018,23(3): 229-237. [12] ZEOLIN,TABBARA H,GU S.CFD modelingofprimary breakup during metal powder atomization [J].Chemical EngineeringScience,2011,66(24):6498-6504. [13] WEIM W,CHENSY,SUN M,etal.Atomizationsimulation and preparation of24CrNiMoY alloy steelpowder using VIGA technology at high gas pressure [J].Powder Technology,2020,367:724-739. [14] FRITSCHING U.Spraysimulation:Modelingandnumerical simulation of spray forming metals [M ]. New York: AmericanSocietyofMechanicalEngineers,2006. [15] LIX G,FRITSCHING U.Processmodelingpressure-swirl- gas-atomizationformetalpowderproduction[J].Journalof MaterialsProcessingTechnology,2017,239:1-17. [16] ASHGRIZ N.Handbook ofatomization andsprays[M]. Boston,MA:SpringerUS,2011. [17] FIRMANSYAH D A,KAISER R,ZAHAF R,et al. Numericalsimulationsofsupersonicgasatomizationofliquid metaldroplets[J].JapaneseJournalofAppliedPhysics,2014, 53(5S3):05HA09. [18] üNAL A.Flow separation andliquidrundownin a gas- atomizationprocess[J].MetallurgicalTransactionsB,1989, 20(5):613-622.