当前位置：首页 » 国检检测新闻中心 » 检测百科 » 分享：基于BP神经网络的板形预测

分享：基于BP神经网络的板形预测

来源：国检检测查看手机网址

扫一扫!

扫一扫!

浏览：- 发布日期：2024-05-16 14:52:43【大中小】

马兵智,

曾卫仔,

宋浩源,

商光鹏

北京首钢冷轧薄板有限公司，北京　101304

摘要:

板带材的板形精度一直是研究的重点。在实际生产过程中影响板形精度的因素很多而且因素之间存在非线性、强耦合的关系，基于板形控制机理的传统数学模型很难准确表达其中的关系，而基于数据驱动的非机理模型则能取得很好的结果。BP神经网络作为一种发展成熟的算法可以作为一种新的预测手段应用在板形的预测工作中。因此，本文将BP神经网络应用于板形的预测研究中，讨论了基于BP神经网络的板形预测模型的可行性以及应用的优势，重点介绍BP神经网络对板形预测带来的积极意义。BP神经网络在对即时板形缺陷系数进行预测时，能够较好的接近实际的拟合值。BP网络在训练过程中，在50轮训练后基本收敛，并且整个训练过程没有产生过拟合现象。BP神经网络对测试集进行预测，能够有效的反映板形的变化情况，且对一次、三次板形缺陷系数的预测结果较好。

随着科学技术的发展，各领域对板带材的质量提出了更高的要求。板带材的质量主要指厚度、宽度和板形等，其中板形质量控制是国内外学者研究的重点。为了得到高质量的板带材，需要实现对板形的高精度控制，常常需要建立相关的板形控制模型。虽然传统的基于板形控制机理的数学模型已经取得了一些成就，但是在模型的参数设置上准确性和合理性存在一些问题[1]，因此许多基于数据驱动的非机理预测模型随之产生。通过预测板形值，可以在板形偏差较大时通过提前修正参数进而提高控制器的性能。因此板形的预测控制方法一直是国内外研究的重点[2]。

近年来，许多学者开始利用数据驱动研究板带质量，同时取得了一些成就。纪阳[3]在研究板形板厚控制(AFC-AGC)时，针对板形板厚控制系统的非线性、强耦合、大时滞的特点，采用了改进粒子群优化算法与RBF神经网络相结合的方法，完成了系统的解耦，实现了分别控制；李超[4]利用网格搜索对支持向量机(SVM)模型的参数进行优化，实现了对六种常见板形缺陷的正确分类。张秀玲[5]等在建立基于Elman网络的板形预测模型时，利用人工蜂群算法(ABC)代替了反传算法，提高了Elman网络的泛化能力，使得板形预测精度更高；陈丽杰[6]针对传统模式识别方法抗干扰能力差、易陷入局部最小值等缺点，采取了免疫遗传算法(IGA)与径向基函数(RBF)神经网络相结合的板形智能识别模型，提高了模型的精度和速度。

通过不断的研究与发展，利用数据驱动研究板带质量的技术越来越成熟，基于此，本文将BP神经网络应用于板形的预测研究中，讨论了基于BP神经网络的板形预测模型的可行性以及应用的优势。

1. 板形介绍

广义上讲，板形统指带材横截面的几何形状和在自然状态下纵向表观的平坦性两个特性[7-9]，包括了凸度、楔形度、边降、局部突起量和平坦度五项内容[10]。但有时在冷轧中仅指产品的纵向平坦度[11,12]。本文提到的板形研究即为研究板带材轧后的纵向平坦度。

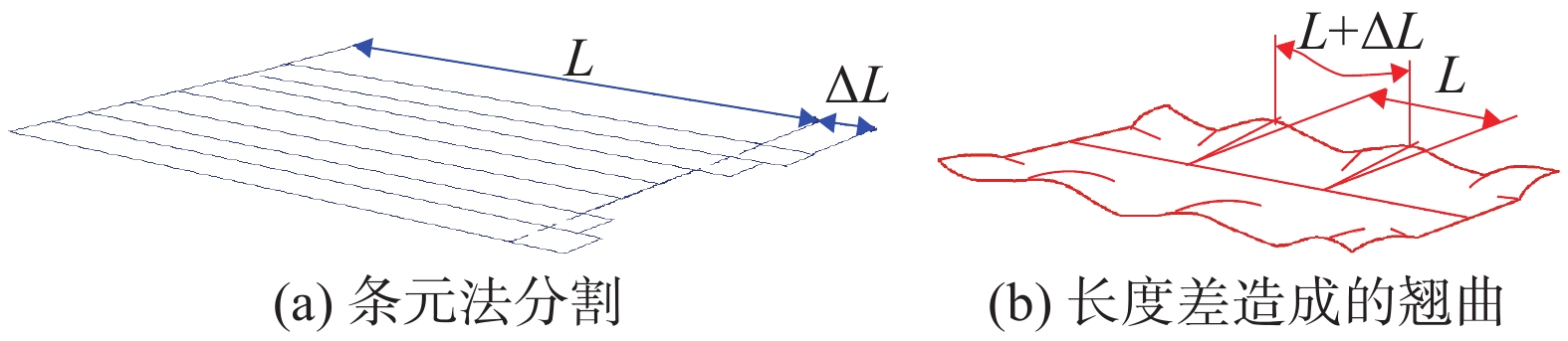
板带材的轧制过程实际上是金属在轧辊的压下作用下发生塑性变形的过程。一定断面形状的坯料经轧制过程会发生明显的纵向延伸和一定的横向流动，把带钢沿宽度方向划分为若干纵条，任一纵条的压下量变化时，都会引起该条的纵向延伸发生变化，并影响到相邻的纵条，如图1所示。由于板带是一个整体，其内部会相互牵扯，互相影响，所以在沿宽度方向的压下量分布不均匀时，会造成板带内部产生内应力，当此内应力足够大时，会引起板带材的翘曲，严重影响板带质量。

图 1 板带材的翘曲

下载: 全尺寸图片幻灯片

板形直观上说的就是板带材的翘曲程度，一般指浪形、瓢曲或旁弯的有无及其程度，实质上指的是由于板带内部残余应力造成的延伸率差。因此平坦度的计算公式为：

?_{w} (?) = \frac{?_{w} (?) - ?_{0}}{?_{0}} \times 10^{5} = - \frac{?_{f} (?)}{?}

(1)

其中， $ρ_{w} (x)$ 为某一段的平坦度， $L_{w} (x)$ 为某条纵向纤维沿带钢表面的实际长度， $L_{0}$ 为自由带钢的某一取定长度区间， $σ_{f} (x)$ 为板形检测应力，E为带钢的弹性模量，定义平坦度的单位为IU。因此1 IU表示1 m长的带钢会发生10 μm的纵向延伸。

2. BP神经网络介绍

20世纪80年代中期，David Runelhart、Geoffrey Hinton和Ronald W-llians、DavidParker等人分别发现了误差反向传播算法(Error Back Propagation Training)，简称BP，系统解决了多层神经网络隐含层连接权学习问题，并在数学上给出了完整推导。人们把采用这种算法进行误差校正的多层前馈网络称为BP神经网络。

BP神经网络具有任意复杂的模式分类能力和优良的多维函数映射能力，解决了简单感知器不能解决的异或(Exclusive OR，XOR)和一些其他问题。从结构上讲，BP网络具有输入层、隐藏层和输出层；从本质上讲，BP算法就是以网络误差平方为目标函数、采用梯度下降法来计算目标函数的最小值。

BP神经网络的基本组成单位是神经元，一个神经元的原理如图2所示。

图 2 神经元原理图

下载: 全尺寸图片幻灯片

则可得神经元的输出：

?_{?} = ?_{?} \times ?_{?} + ?

(2)

?_{?} = ? (?_{?})

(3)

其中，xn为神经元输入向量，zn为神经元输出向量，wn为神经元权重向量，b为神经元阈值，f为神经元激活函数。

对于一个具有输入层、隐含层、输出层的BP神经网络，有

? (?) = (?_{1} (?), ?_{2} (?), . . . ?_{?} (?))

(4)

? (?) = (?_{1} (?), ?_{2} (?), . . . ?_{?} (?))

(5)

其中， $x (k)$ 为输入向量， $d (k)$ 为期望输出。则隐含层输入向量为

?_{? ?} (?) = \sum_{? = 1}^{?} ?_{? ?} ?_{?} (?) + ?_{?}, ? = 1, 2, . . . ?

(6)

隐含层输出向量为

?_{? ?} (?) = ? (?_{? ?} (?)), ? = 1, 2, . . . ?

(7)

输出层输入向量为

?_{? ?} (?) = \sum_{? = 1}^{?} ?_{? ?} ?_{? ?} (?) + ?_{?}, ? = 1, 2, . . . ?

(8)

输出层输出向量为

?_{? ?} (?) = ? (?_{? ?} (?)), ? = 1, 2, . . . ?

(9)

其中， $h_{i h}$ 为隐含层输入向量， $h_{o h}$ 为隐含层输出向量， $y_{i o}$ 为输出层输入向量， $y_{o o}$ 为输出层输出向量， $w_{i h}$ 为输入层与隐含层的连接权值， $w_{h o}$ 为隐含层与输出层的连接权值， $b_{h}$ 为隐含层各神经元的阈值， $b_{o}$ 为输出层各神经元的阈值， $k_{}$ 为样本数据个数， $p_{_{}}$ 为输入层节点数， $q_{_{}}$ 为输出层节点数， $f$ 为神经元激活函数。

? = \frac{1}{?} \sum_{? = 1}^{?} (?_{?} (?) - ?_{? ?} (?))^{2}

(10)

计算误差函数e对输出层各神经元的偏导数，根据输出层期望输出和实际输出以及输出层输入等参数计算。

\frac{\partial ?}{\partial ?_{? ?}} = \frac{\partial ?}{\partial ?_{? ?}} \frac{\partial ?_{? ?}}{\partial ?_{? ?}} = ?_{?} (?) ?_{? ?} (?)

(11)

\begin{aligned} \frac{\partial ?}{\partial ?_{? ?}} = & - \frac{2}{?} (?_{?} (?) - ?_{? ?} (?)) ?_{? ?}^{'} (?) = \\ - (?_{?} (?) - ?_{? ?} (?)) ?^{'} (?_{? ?} (?)) = ?_{?} (?) \end{aligned}

(12)

\frac{\partial ?_{? ?} (?)}{\partial ?_{? ?}} = ?_{? ?} (?)

(13)

定义 $δ_{o} (k)$ 为输出层的灵敏度。计算误差函数对隐藏层各神经元的偏导数，根据后一层（这里即输出层）的灵敏度 $δ_{o} (k)$ ，后一层连接权值w，以及该层的输入值等参数计算：

\frac{\partial ?}{\partial ?_{? ?}} = ?_{?} (?) ?_{?} (?)

(14)

\frac{\partial ?}{\partial ?_{? ?}} = - (\sum_{? = 1}^{?} ?_{?} (?) ?_{? ?} ?^{'} (?_{? ?} (?)) = ?_{?} (?)

(15)

\frac{\partial ?_{? ?} (?)}{\partial ?_{? ?}} = ?_{?} (?)

(16)

利用误差函数e对输出层各神经元的偏导数来修正输出层连接权值：

Δ ?_{? ?} (?) = - ? \frac{\partial ?}{\partial ?_{? ?}} = - ? ?_{?} (?) ?_{? ?} (?)

(17)

?_{? ?}^{? + 1} = ?_{? ?}^{?} + ? ?_{?} (?) ?_{? ?} (?)

(18)

式中， $η$ 为学习率。

利用误差函数e对隐含层各神经元的偏导数来修正输出层连接权值：

Δ ?_{? ?} (?) = - ? \frac{\partial ?}{\partial ?_{? ?}} = - ? ?_{?} (?) ?_{?} (?)

(19)

?_{? ?}^{? + 1} = ?_{? ?}^{?} + ? ?_{?} (?) ?_{?} (?)

(20)

计算全局误差：

? = \frac{1}{? \times ?} \sum_{? = 1}^{?} \sum_{? = 1}^{?} (?_{?} (?) - ?_{?} (?))^{2}

(21)

最终的目标是使全局误差最小，此时的预测精度最高。

3. BP神经网络回归预测板形

数据集采用钢种HC340/590DP，出口厚度1.614 mm，出口宽度1453.9 mm，共16卷。选取15卷作为训练集，在训练集中选取20%作为验证集，剩余1卷作为测试集。然后对钢卷的所有特征进行筛选，将数字量（只有0，1）去除，并去除掉pearson相关性系数大于0.95的特征，剩下539个特征，如表1所示。由于调控功效被分为80段离散值，为匹配，对每个时刻的62段板形测量值插值成80段值后进行勒让德多项式拟合，获得各基模式的系数（后称为板形缺陷系数），在输入中加入这一时刻的板形缺陷系数，以下一时刻的板形缺陷系数作为输出对板形进行回归预测。此次BP神经网络选用节点数分别为输入层节点数544，隐含层节点数35，输出层节点数5。损失函数MSE，优化器为Adam。如图3所示为BP神经网络在整个训练过程中损失函数的变化情况，可以看出模型在训练集的损失函数在训练初期急速下降，之后下降速率减慢并趋于平缓，说明模型的精度在逐步上升，没有明显的过拟合现象。

表 1 BP神经网络回归预测特征