分享:固态相变和软化效应对超高强钢焊接残余应力的影响
王重阳1, 韩世伟2, 谢峰2, 胡龙1, 邓德安1( ) )
|
|
1重庆大学 材料科学与工程学院 重庆 400045 2重庆铁马工业集团有限公司 重庆 400050 |
|
摘要:
以板厚为5 mm的1600 MPa级超高强钢为研究对象,采用熔化极惰性气体保护焊(MIG)焊接方法和ER307Si焊丝制备了单道对接接头,分别利用盲孔法和显微硬度仪测量残余应力和接头硬度分布。基于接头热影响区和软化区的硬度测量结果,以SYSWELD软件为平台,开发了考虑超高强钢固态相变和软化效应以及焊缝金属加工硬化和退火软化的“热-冶金-力学”多场耦合的有限元计算方法。采用该方法模拟了超高强钢单道对接接头的温度场及残余应力,并与实验结果进行了比较。基于数值模拟结果探讨了固态相变和软化效应对焊接残余应力的影响机制。数值模拟结果表明,固态相变对纵向残余应力的大小和分布有显著影响;对横向残余应力的大小和分布有一定程度的影响。软化效应对纵向残余应力的峰值有较显著的影响,对横向残余应力几乎没有影响。将数值模拟结果与实验结果比较可知,在同时考虑固态相变和软化效应的情况下,平板对接接头的焊接残余应力计算结果与实验测量结果最为吻合。 |
| 关键词 : 超高强钢, 固态相变, 软化效应, 焊接残余应力, 数值模拟 |
以板厚为5 mm的1600 MPa级超高强钢为研究对象,采用熔化极惰性气体保护焊(MIG)焊接方法和ER307Si焊丝制备了单道对接接头,分别利用盲孔法和显微硬度仪测量残余应力和接头硬度分布。基于接头热影响区和软化区的硬度测量结果,以SYSWELD软件为平台,开发了考虑超高强钢固态相变和软化效应以及焊缝金属加工硬化和退火软化的“热-冶金-力学”多场耦合的有限元计算方法。采用该方法模拟了超高强钢单道对接接头的温度场及残余应力,并与实验结果进行了比较。基于数值模拟结果探讨了固态相变和软化效应对焊接残余应力的影响机制。数值模拟结果表明,固态相变对纵向残余应力的大小和分布有显著影响;对横向残余应力的大小和分布有一定程度的影响。软化效应对纵向残余应力的峰值有较显著的影响,对横向残余应力几乎没有影响。将数值模拟结果与实验结果比较可知,在同时考虑固态相变和软化效应的情况下,平板对接接头的焊接残余应力计算结果与实验测量结果最为吻合。
关键词:
进入21世纪以来,随着低合金高强钢和超高强钢在车辆、桥梁、船舶、工程机械、海洋工程、高层建筑以及能源装备等制造领域获得越来越广泛的应用,实际工程结构轻量化和大型化的制造需求对钢铁材料的强度与韧性提出了更严苛的要求[1,2]。我国自1997年启动“新一代微合金高强高韧钢的基础研究”国家攀登计划项目以来,经过20余年发展,在低合金高强钢与超高强钢的开发与应用方面取得了长足的进步[3]。近年来,国内钢铁企业开发的特种钢(如61X钢)和耐磨钢(如NM450TP)等淬火钢就是在这一背景下研制出的新型低成本低合金超高强钢。
目前,国产低合金超高强淬火钢的生产方式主要有2种,一种是离线淬火工艺,另一种是在线淬火工艺。对于屈服强度大于1000 MPa的超高强度淬火钢而言,采用等强匹配的焊接材料来实施焊接仍然是一个世界性的难题[4,5]。因此,对于这类钢的焊接,目前还是以防止焊接冷裂纹和控制接头韧性为主的原则来选择填充材料。从对实际工程中超高强淬火钢使用的焊接材料调查来看,当前采用的焊接材料主要有2类,一类是奥氏体不锈钢焊材,另一类是熔覆金属强度不高于1000 MPa的焊丝或焊条。前者主要用于坦克和装甲车的焊接,后者主要用于各类工程车辆如自卸车、矿山工程车和垃圾运输车的焊接。
到目前为止,国内外学者对超高强淬火钢的焊接物理冶金问题、焊接填充材料及焊接工艺等方面进行了一定程度的研究[6~8],但对焊接残余应力的研究还非常有限。
理论上,焊接接头的残余应力峰值与母材及填充金属的屈服强度成正比,材料强度越高,焊接产生的残余应力峰值也会越高,而且很多情况下由于加工硬化、固态相变及强拘束等因素使得焊接残余应力峰值会达到甚至大幅超过材料常温屈服极限[9]。加之超高强钢经常用于制造薄板或薄壁结构,由于这类结构本身刚度较低[10],因此与普通低碳钢及低合金高强钢相比,超高强钢的焊接残余应力和变形问题更加突出[11,12]。一方面,在焊接过程中产生的瞬态应力是热裂纹和冷裂纹产生的驱动力;另一方面,焊接产生的拉伸残余应力是结构在服役过程中发生脆性断裂、疲劳失效和应力腐蚀的主要影响因素,产生的压缩残余应力则会增加结构失稳的风险。研究[13]表明,在残余应力与载荷应力叠加的动载服役条件下,超高强钢焊接热影响区脆化和软化区极易成为疲劳裂纹的启裂点,产生的裂纹会快速扩展直至结构瞬时失稳断裂。因此,非常有必要对超高强钢的焊接残余应力问题进行深入研究。
尽管现有的实验方法可以用于测量残余应力,但是其工作量大且费用高,而且大多方法只能获得焊件表面有限位置的残余应力。同时,由于绝大多数实验方法属于有损检测方法,因此很难直接用于测量实际焊接结构的残余应力。近年来,计算焊接力学方面取得的进展表明,数值模拟方法是获得焊接接头乃至整体焊接结构残余应力的最有潜力的手段。
在焊接过程中,超高强钢焊接接头热影响区会发生以马氏体相变为主体的固态相变。本课题组[14]前期研究了固态相变对P92钢焊接接头残余应力的影响,结果表明,固态相变对焊接残余应力的形成有显著影响,不仅可以改变残余应力的大小,还可以改变应力的符号。方金祥等[15]研究了固态相变对马氏体钢激光熔覆成形过程应力演化的影响,分析结果表明,与只考虑热-力耦合的模型计算结果相比,考虑固态相变情况下的有限元结果与实验值更为吻合,残余应力水平显著降低且分布规律明显不同。另外,在焊接超高强淬火钢时,焊接接头紧邻热影响区的母材处还会出现严重的软化现象。Nishimura等[16]对1180 MPa级调质钢薄板搭接接头的残余应力进行了研究,从数值模拟结果和实验结果来看,紧邻热影响区的母材软化对该区域的残余应力大小有显著的影响。李恒等[17]对异种钢焊接接头各区域的组织性能进行分析,结果表明,软化区附近高强钢耐磨性下降以及焊接接头整体强度下降,强度级别高的接头软化现象更为严重。因此,在采用数值模拟方法模拟超高强淬火钢的焊接残余应力时,需要建立能同时考虑固态相变和软化效应的材料模型,并且有必要研究这些因素对残余应力大小与分布的影响程度。
本工作以板厚为5 mm的1600 MPa级超高强淬火钢为研究对象,首先采用熔化极惰性气体保护焊 (melt inert-gas welding,MIG)焊接方法和ER307Si焊丝制备单道对接接头,分别利用热电偶、盲孔法和显微硬度仪测量典型位置的焊接温度循环、工件表面的残余应力和接头硬度分布。随后,基于热影响区和软化区的硬度测量结果,以SYSWELD软件为平台,开发了考虑超高强钢固态相变和软化效应以及焊缝金属加工硬化和退火软化的“热-冶金-力学”多场耦合的有限元计算方法。采用所开发的计算方法模拟了超高强钢单道对接接头的温度场及残余应力,并与实验结果进行比较。基于数值模拟结果探讨了固态相变和软化效应对焊接残余应力的影响机制,以期为深入理解超高强淬火钢在低强匹配焊接条件下的残余应力分布特征提供实验依据和理论支撑。
1 实验方法
1.1 焊接接头制备
实验所用被焊材料(以下简称为母材)为某特种车辆用超高强钢(供货状态为淬火态),其主要化学成分(质量分数,%)为:C 0.26,Si 0.32,Mn 1.7,P < 0.015,S < 0.008,Ni 0.55,Cr 0.62,Mo 0.35,Fe余量。焊接填充材料为ER307Si不锈钢焊丝,焊丝直径为1.2 mm,其主要化学成分(质量分数,%)为:C 0.074,Si 0.12,Mn 1.69,P 0.017,S 0.001,Ni 9.75,Cr 19.1,Mo 0.01,Cu 0.007,Fe余量。图1为焊接平板试件的几何尺寸示意图,试件尺寸为300 mm × 300 mm × 5 mm,坡口形式为V型坡口,坡口角度为60°。
图1
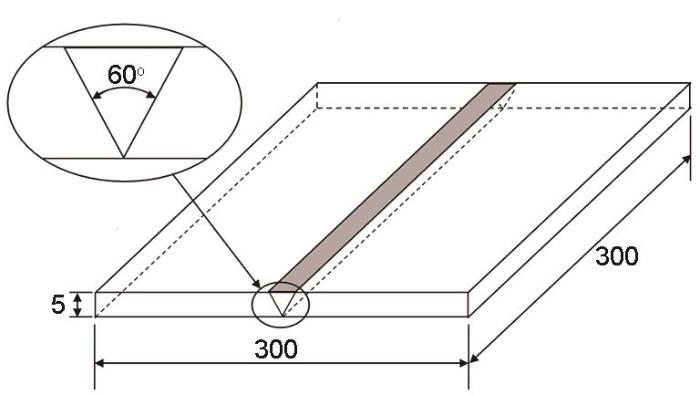
图1 焊接试件几何尺寸示意图
Fig.1 Schematic of dimensions of welded joint (unit: mm)
在无外部拘束的条件下,采用MIG焊接方法进行单道焊的焊接,焊接工艺参数为:焊接电流156 A,电弧电压21 V,焊接速率5.66 mm/s,Ar气流量为8 L/min。焊接过程中,采用2个K型热电偶测量焊接热循环,测量点位于焊道中间段的上表面,与焊缝坡口的距离分别为3.0和8.5 mm。
1.2 残余应力测量
焊接完成后,采用盲孔法测量平板对接接头上表面中央区域的残余应力,测量过程符合标准ASTME837-08,应变片的布置位置如图2所示,应变片粘贴在平板对接接头上表面70 mm × 80 mm的中央区域内,其中焊缝上表面1片应变片,焊缝两侧各5片应变片。
图2
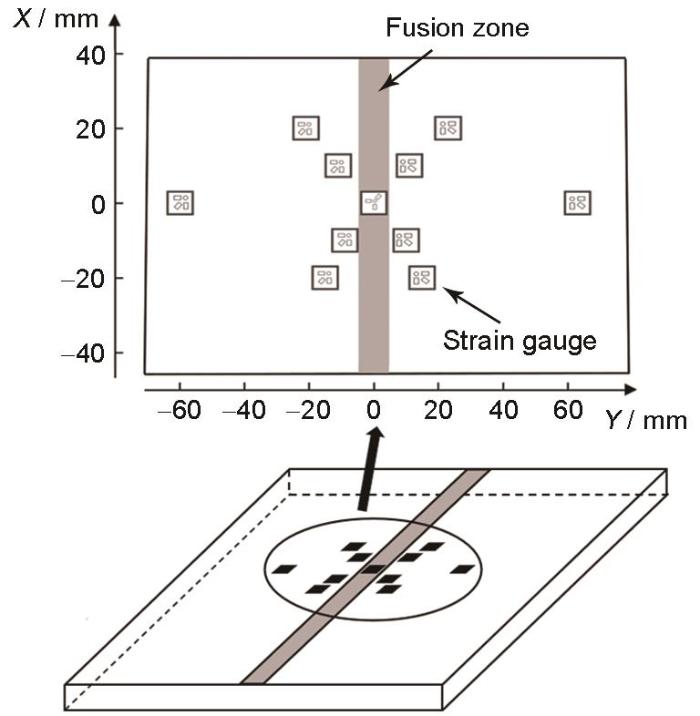
图2 应变片布置位置示意图
Fig.2 Schematics of arrangement of strain gauges
1.3 显微硬度测量
残余应力测量完成后,采用线切割方法在焊接试件中央截取金相试样,将金相试样打磨和抛光后,采用HX1000 TM/LCD显微硬度仪测量显微硬度,测量过程符合标准GB/T 4340.1—2009。测量点分布在如图3所示的直线L1上,L1距平板对接接头上表面1 mm,其中,在应力梯度较大的区域采用0.25 mm测量间隔,应力梯度较小的区域采用0.5或1.0 mm测量间隔,该线上的点涵盖焊缝(FZ)、热影响区(HAZ)和母材(BM) 3个区域。测量参数如下:压力为9.8 N,加载时间为15 s。
图3

图3 显微硬度测量点位置示意图
Fig.3 Schematic of measuring points of microhardness (unit: mm, FZ—fusion zone, HAZ—heat affected zone, BM—base metal)
1.4 高温力学性能及相变温度点测量
根据GB/T 228.1—2021《金属材料拉伸试验》标准,采用线切割方法在超高强淬火钢板上取出拉伸试样,在万能拉伸试验机上进行常温、200℃、400℃、600℃和800℃高温拉伸实验,测量材料在各温度点的屈服强度。按照直径6 mm、长25 mm的尺寸规格,采用线切割方法制备热膨胀系数测量试样。在热膨胀测量仪中,以10℃/min加热到1000℃,再以20℃/min冷却到室温,基于实验结果确定材料在各温度段的线膨胀系数以及相变温度点。
2 数值模拟方法
在焊接残余应力数值模拟中,对于母材考虑了马氏体、奥氏体和软化相。母材在奥氏体转变开始温度(Ac1)以下的加热过程中,淬火马氏体转变为软化相,继续加热到Ac1温度以上时,软化相开始转变为奥氏体相,当温度达到奥氏体转变结束温度(Ac3)时奥氏体化完成;冷却过程中,热影响区的过冷奥氏体转变为正火马氏体(焊态马氏体)。由于正火马氏体和淬火马氏体的硬度差异很小(详见3.1节),在本工作中,淬火马氏体相和正火马氏体相采用了相同的材料参数。
本工作采用的焊缝填充材料为ER307Si奥氏体不锈钢,计算温度场和应力场时采用了文献[18]中的高温热物理性能和力学性能参数。对于奥氏体不锈钢而言,除了要考虑热物理性能参数和力学性能参数随温度的变化,还需要考虑加工硬化和退火软化效应对残余应力的影响,本工作采用各项同性硬化模型[19]考虑加工硬化,采用阶跃退火模型[20]考虑退火软化效应,设定奥氏体不锈钢的退火温度为1000℃[20]。
2.1 有限元模型建立
在数值模拟中,根据实际试件的几何尺寸,建立了如图4所示的有限元模型。图中,V箭头所指方向为焊接方向;为了平衡计算效率和计算精度,在焊缝及其附近区域采用较为细密的网格,而在远离焊缝的区域采用相对稀疏的网格,其中所有单元均为8节点六面体单元,单元总数为60000,节点总数为69794。
图4
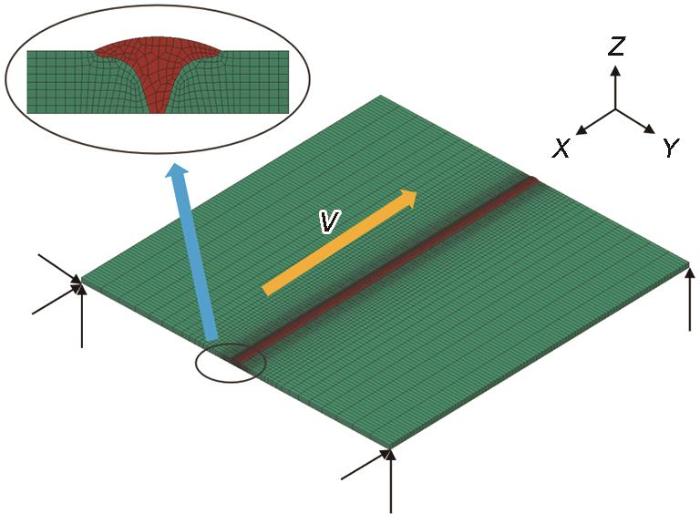
图4 有限元模型示意图
Fig.4 Schematic of finite element model (FEM) (Inset shows welding direction and relative size of the finite element mesh, V—welding speed)
2.2 温度场计算
在温度场计算中,采用Goldak等[21]提出的双椭球热源模型模拟焊接热输入,热量在焊接试件内部的传导过程用非线性传热方程[22]描述,同时分别采用Newton冷却方程[23]和Stefan-Boltzmann定律[23]考虑试件与环境的对流热交换和试件的辐射散热。在温度场计算时,设定试件初始温度及环境温度均为30℃,模拟时使用的焊接参数与实验时采用的参数完全一致。
超高强钢马氏体相和奥氏体相的高温热物理性能参数如图5所示。其中马氏体和奥氏体各温度点的密度相同,热导率和比热容在部分或全部温度点有所差异,该部分参数由JMatPro软件根据超高强钢的材料成分计算得来,其中软化相的热物理性能参数与马氏体相同[24,25]。
图5
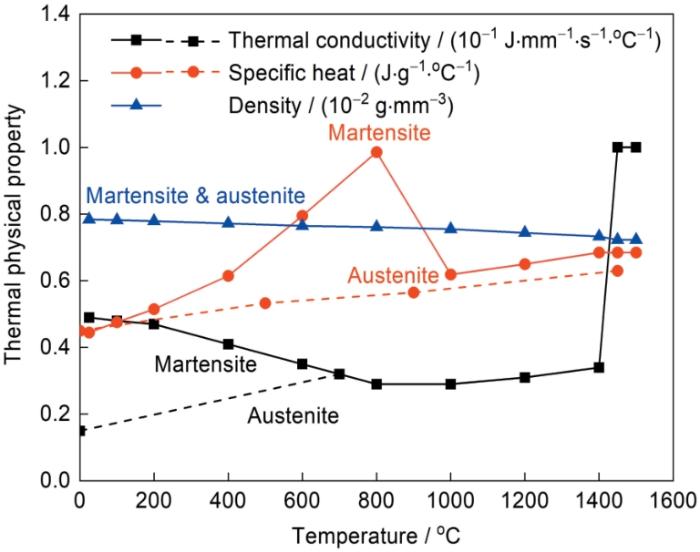
图5 超高强钢的热物理性能参数
Fig.5 Temperature-dependent thermal properties of ultra-high strength steel (UHSS)
2.3 组织计算
在加热和冷却过程中,超高强钢会分别经历奥氏体转变和马氏体相变。从热膨胀实验结果(图6)可知,母材的Ac1为720℃,Ac3为850℃;冷却过程中马氏体相变开始温度(Ms)为525℃。由图6所示的温度-应变曲线可以确定马氏体和奥氏体的热膨胀系数。在数值模拟时,假定软化相的热膨胀系数与马氏体相同,分别采用Johnson-Mehl-Avrami关系[26]和Koisten-Marburger关系[27]描述奥氏体转变过程和马氏体相变过程。
图6
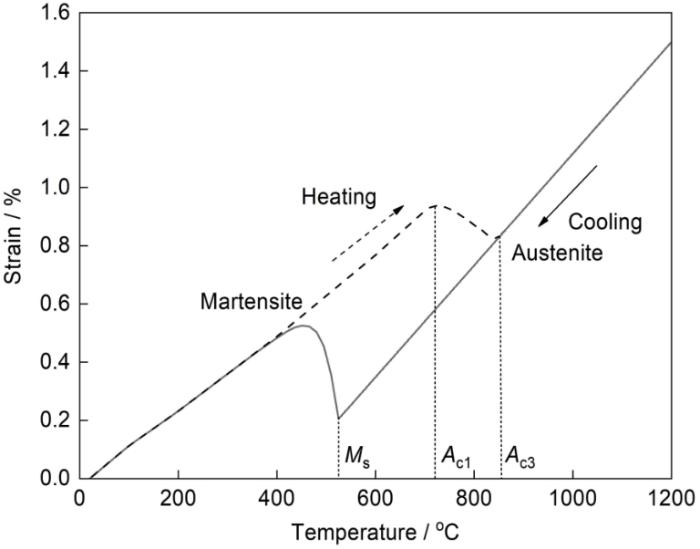
图6 超高强淬火钢加热和冷却过程中的温度-应变曲线
Fig.6 Temperature-strain curves of UHSS during heating and cooling (Ms—martensite transformation start temperature, Ac1—austenization start temperature, Ac3—austenization finish temperature)
2.4 软化模型
由于超高强钢的供货状态为淬火马氏体,因此在焊接时,紧邻热影响区的母材会在焊接热循环的作用下发生一定程度的软化,即材料的屈服强度和硬度均有所降低。从理论上分析,软化效应会对残余应力产生影响,因此在数值模拟中需要考虑这一因素。
在本工作中,建立了包含“软化系数”和“最大软化程度”的模型来考虑超高强钢在焊接过程中的软化现象。依据数值模拟得到的峰值温度分布结果和实验测量的硬度分布结果,确定峰值温度和软化系数的对应关系。由于母材为淬火马氏体,理论上,Ac1对应位置的软化程度最高,而峰值温度越低软化程度越小。从硬度测量结果(详见3.1节)与数值模拟温度场结果(详见3.2节)来看,峰值温度为230℃以下时硬度几乎不受影响,因此软化温度范围可以确定为230~720℃ (Ac1)。为了对“软化系数”(ft)进行定量评价,设定峰值温度为230℃时ft为0,峰值温度为720℃时ft为1,峰值温度与ft之间的关系定义如下:
式中,TH为最高峰值温度(720℃);TL为最低峰值温度(230℃);Tt为软化区任意位置的峰值温度(TL ≤ Tt ≤ TH)。
在本工作中,最大软化程度(D)根据软化区的最低硬度与母材的平均硬度的差值来确定,定义如下:
式中,HVBM为母材的平均硬度,HVmin为软化区最低硬度。
由于本工作没有实测软化区的屈服强度,在数值模拟中将硬度的最大软化程度等效为屈服强度的最大软化程度。从硬度实验结果来看,峰值温度为720℃时,硬度最低,此位置对应屈服强度最低,该位置母材各温度点的的屈服强度(σf)可由
式中,σs为超高强钢母材焊接前各温度点的屈服强度。
母材经历的峰值温度Tt在TH与TL之间时,冷却过程中Tt以下各个温度的屈服强度σt由ft加权计算得到:
本工作中建立的软化模型如图7所示,其中σs与图8中马氏体720℃以下的屈服强度相同;σf为超高强钢母材经过峰值温度720℃软化后的屈服强度;σt为超高强钢母材经过峰值温度Tt软化后的屈服强度(Tt以上温度点的屈服强度不变)。
图7
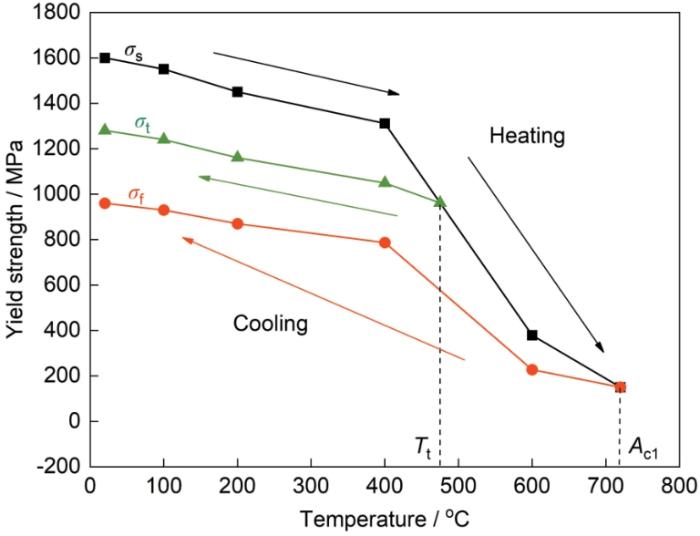
图7 软化模型示意图
Fig.7 Schematic of softening model (σs—yield strength without softening during heating stage, σf—yield strength with softening and the peak temperature is 720oC during cooling stage, σt—yield strength with softening and the peak temperature is Tt during cooling stage)
图8
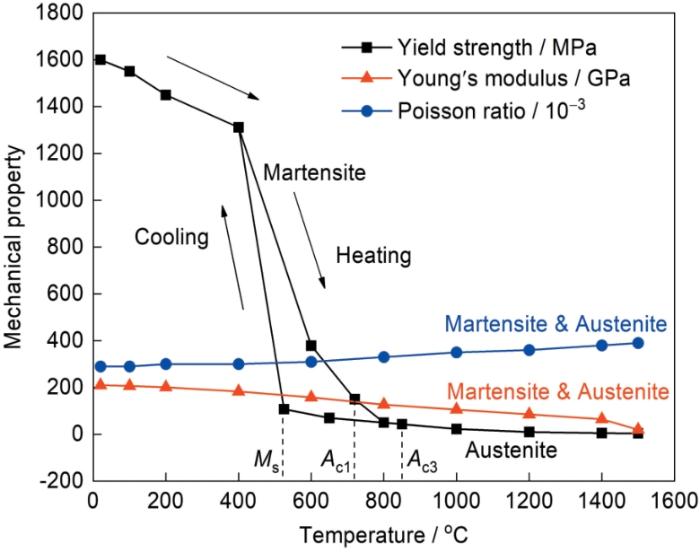
图8 超高强钢的力学性能参数
Fig.8 Mechanical property parameters of UHSS
2.5 应力计算
对于考虑固态相变的超高强淬火钢材料而言,材料的总应变由5部分组成:弹性应变、塑性应变、热应变、相变塑性应变和蠕变应变。但考虑到在焊接过程中,材料在高温停留时间较短,蠕变应变并不明显,因此在总应变中可以忽略蠕变应变。其中,弹性应变和塑性应变分别采用Hooke定律和Von Mises屈服准则计算,热应变由热膨胀系数反映,相变应变采用Leblond模型[28]描述。软化效应采用本工作提出的模型来考虑。
由于超高强钢自身强度较高,加工硬化效应不明显,因此在材料模型中定义为理想弹塑性模型,不考虑加工硬化的影响。超高强钢的力学性能参数如图8所示,其中常温、200℃、400℃、600℃和800℃的屈服强度由拉伸实验得到,其余材料性能参数由JMatPro软件通过材料成分计算得到。从图8中可以看出,由于超高强钢的初始状态为淬火马氏体相,其屈服强度在焊接加热过程中不断降低,在Ac1至Ac3区间发生奥氏体化,高温时完全为奥氏体相,因而屈服强度很低;冷却过程中,奥氏体温度不断降低,温度较低时为过冷奥氏体相,屈服强度不断升高,当温度低于Ms,由于发生马氏体相变,生成正火马氏体相,屈服强度急剧升高,直至达到初始相的屈服强度。
在实验中没有采用任何外部拘束,因此在有限元模型中仅采用三节点六自由度的拘束方式来防止刚体位移,力学边界条件如图4所示。
2.6 计算案例
本工作的主要目的是澄清固态相变和软化效应对超高强钢对接接头焊接残余应力的影响,因此共设计了3种计算案例,如表1所示:A案例不考虑固态相变和软化效应,B案例仅考虑固态相变,C案例同时考虑固态相变和软化效应。
表1 计算案例
Table 1
| Case | SSPT | SE |
|---|---|---|
| A | No | No |
| B | Yes | No |
| C | Yes | Yes |
3 结果与讨论
3.1 显微硬度
图9为焊接接头沿L1的显微硬度分布。由图可见,在紧邻热影响区的母材侧存在一个较宽的软化区(SZ)。由于母材为淬火态马氏体,在焊接热循环条件下,该区域发生回火软化现象,紧邻热影响区位置的软化程度最严重,其硬度为312 HV,随着距离热影响区位置越来越远,软化程度逐渐降低。通过
图9
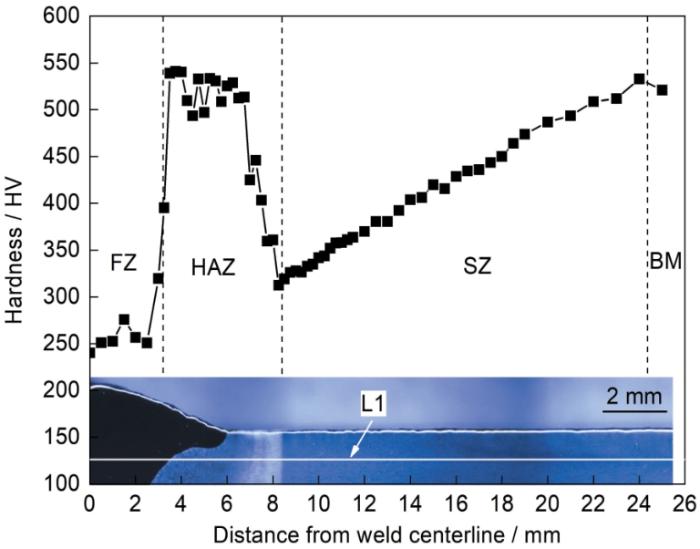
图9 焊接接头的显微硬度分布
Fig.9 Microhardness distributions of welded joint (SZ—softening zone. Inset shows the location of micro-hardness measurement)
从焊接接头的显微硬度分布图可以看出,超高强钢的固态相变和软化效应均十分显著,对于提高超高强淬火钢焊接接头的残余应力计算精确度来说,在数值模拟中考虑固态相变和母材软化效应是十分必要的。
3.2 温度场
在实验中测量了距离焊趾3.0和8.5 mm的热循环,在数值模型中也取了相应位置P1和P2的热循环,计算结果和实验结果的对比如图10所示。由图可见,实验测量得到的P1和P2峰值温度与数值模拟结果非常接近,2者的差值小于10℃。从加热部分的曲线可以看到,在0~25 s内,实验值与计算值在加热速率上有一定差异。从冷却部分的曲线可以看到,在时间为60 s时,实验值与计算值差距最大,P1点的实测值与计算值之差为39℃,P2点的差值为21℃。尽管P1和P2点的热循环计算结果与实验结果在加热和冷却阶段有一定的差异,但总体而言二者吻合较好。
图10
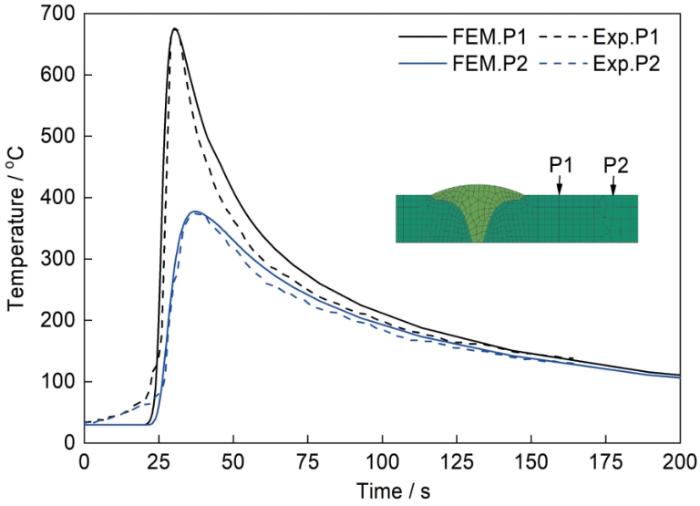
图10 焊接温度循环计算结果和实验结果对比
Fig.10 Comparison of computational results and experimental (Exp.) results of welding temperature cycles (Inset shows the locations of P1 and P2 in the FEM)
从数值模拟温度场结果中提取出中央断面沿L1的峰值温度分布,结果如图11所示。与焊接接头沿L1的显微硬度分布图(图9)相对比,得到软化区的最高峰值温度为720℃ (Ac1),软化区的最低峰值温度为230℃,由此根据2.4节软化模型部分建立完整的软化模型,进行焊接残余应力计算。
图11
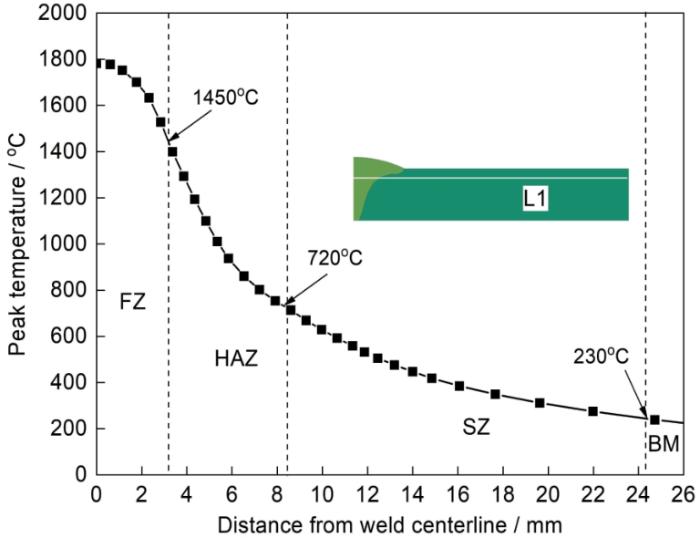
图11 沿L1的峰值温度分布
Fig.11 Distribution of peak temperatures along L1 (Inset shows the location of L1 in the FEM)
3.3 残余应力
在进行残余应力结果讨论之前,为了方便理解,先将“上表面”、“中央断面”和“中央断面上表面”这3个位置绘制示意图,如图12所示。其中图12a中的灰色区域为“上表面”,图12b中的灰色区域为“中央断面”,图12c中的加粗实线为“中央断面上表面”。
图12

图12 上表面、中央断面和中央断面上表面示意图
Fig.12 Schematics of the top surface (a), the central section (b), and the top surface cross-section (c)
图13为超高强钢对接接头3种计算案例的上表面纵向残余应力分布云图。由图可见,3种计算案例的纵向残余应力分布均具有左右对称性,且由于几何端部效应[29]影响,模型两端的纵向应力分布比较复杂,在2个端部及其附近以外的区域,纵向残余应力的分布基本一致,这一区域也可以看成是纵向应力分布稳定区域。与Case A相比,Case B在纵向残余应力分布上发生了较显著的变化,Case B上表面的峰值拉伸应力明显小于Case A,在上表面中央区域Case B的拉伸应力存在范围要明显宽于Case A,此外,Case B上表面的压缩应力形态与Case A有明显差异。从2者的比较可知,固态相变对纵向残余应力计算结果的大小和分布有较显著的影响。与Case B相比,尽管Case C考虑了软化效应,但是2者的上表面纵向应力分布并无显著变化。
图13
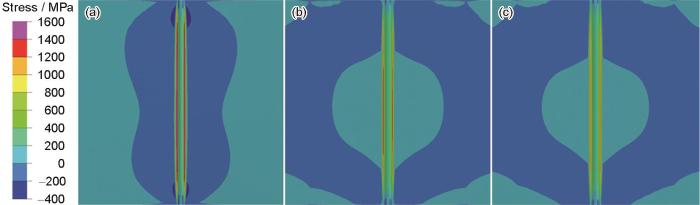
图13 超高强钢对接接头3种计算案例的上表面纵向残余应力云图
Fig.13 Distributions of welding residual stresses of top surface at longitudinal direction under case A (a), case B (b), and case C (c) of UHSS butt joint
图14为超高强钢对接接头3种计算案例的中央断面纵向残余应力分布云图。可以看出,在Case A的热影响区产生了与材料常温屈服强度相当的纵向拉伸残余应力,随着离焊缝的距离逐渐增加,残余应力逐渐降低并转变为压应力。与Case A相比,由于Case B中考虑了固态相变,在热影响区的拉伸残余应力明显减小,这是由于邻近焊缝的热影响区在冷却过程中发生了马氏体相变,其产生的体积膨胀使得该部位拉应力减小,从而使得纵向应力峰值区域明显减小。在Case B的中央断面上,峰值拉伸残余应力出现在紧邻热影响区的母材上。与Case B相比,Case C的热影响区纵向拉伸残余应力的大小和分布变化并不明显,而紧邻热影响区的纵向拉伸残余应力的峰值有显著的降低,这是因为在Case C中考虑了软化效应。
图14
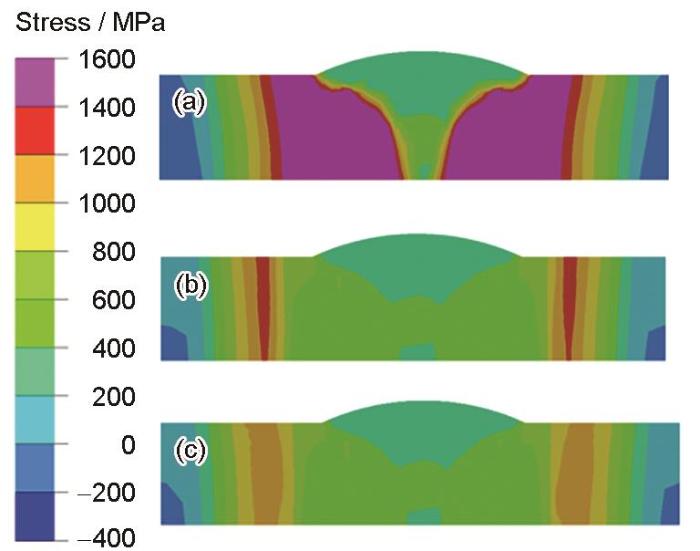
图14 超高强钢对接接头3种计算案例的中央断面纵向残余应力云图
Fig.14 Distributions of welding residual stresses of central section at longitudinal direction under case A (a), case B (b), and case C (c) of UHSS butt joint
图15是超高强钢对接接头3种计算案例中央断面上表面的纵向残余应力分布图,同时盲孔法测量结果也显示在图中。从数值计算结果看,3种计算案例焊缝区域纵向残余应力的分布和大小几乎没有差异;由于考虑了焊缝填充金属(奥氏体不锈钢)的加工硬化作用,其拉伸应力峰值高于材料常温时的屈服极限(图15a)。从3种计算案例的计算结果来看,纵向拉伸残余应力分布在距焊缝中心左右10 mm范围(图15b)。从Case A的纵向残余应力分布可以看出,在紧邻焊缝两侧的热影响区上有很高的拉伸应力,其峰值为1641 MPa,略高于材料的常温屈服极限(1600 MPa)。从Case B纵向残余应力分布中可以看出,由于考虑了固态相变,热影响区纵向残余应力的大小与Case A相比有显著下降,在紧邻热影响区的母材上出现了峰值为1339 MPa的纵向残余应力。从Case C纵向残余应力分布中可以看出,在同时考虑固态相变和软化效应的条件下,与Case B相比,热影响区纵向残余应力的大小与分布没有变化,但是紧邻热影响区的母材上纵向拉伸残余应力峰值显著下降,其峰值为1032 MPa。从3种计算案例得到的纵向残余应力分布计算结果与实验测量结果比较可知,Case C的计算结果与实验测量结果最为吻合。对超高强钢而言,为了获得更高精度的残余应力计算结果,有必要同时考虑固态相变和软化效应。
图15
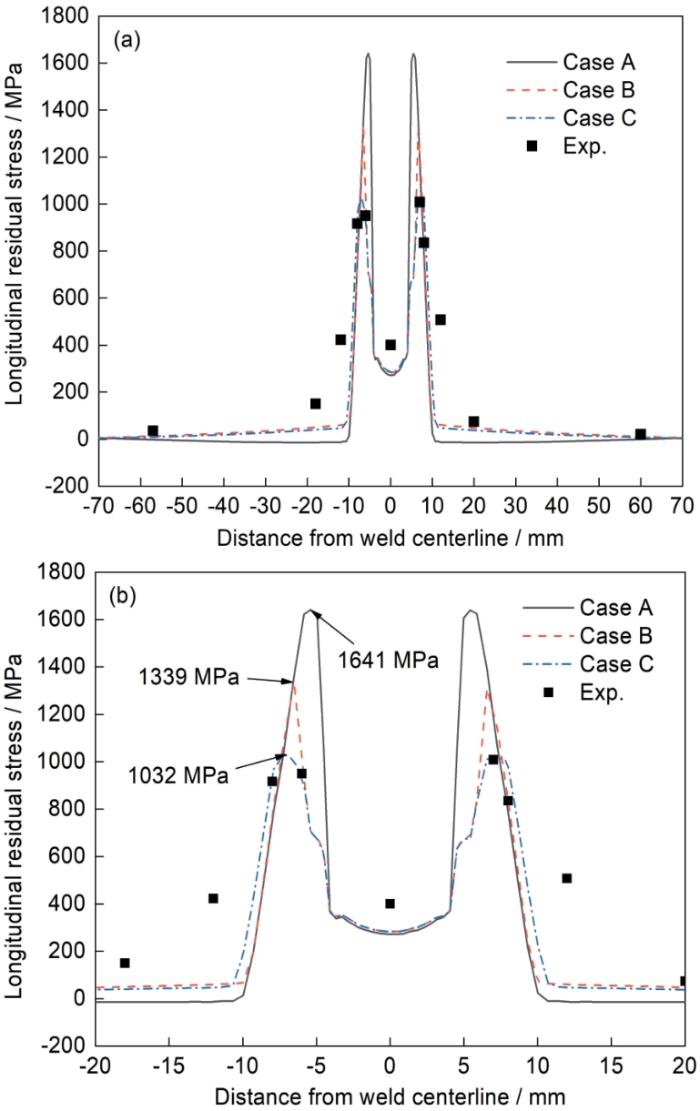
图15 超高强钢对接接头3种计算案例的中央断面上表面纵向应力分布计算结果与实验测量结果对比
Fig.15 Comparisons of longitudinal welding residual stresses along center line of the top surface cross-section between computational and experimental results (a) and local magnified curves (b) under case A, case B, and case C of UHSS butt joint
图16为3种计算案例的上表面横向残余应力分布云图。可以看出,与Case A相比,Case B在横向残余应力分布上发生了一定程度的变化,压缩应力存在区域与Case A有明显差异,但2者峰值拉伸应力相差不大。从2者的比较可知,固态相变对横向残余应力计算结果的大小和分布有一定程度的影响。与Case B相比,尽管Case C考虑了软化效应,但是2者的上表面横向应力分布和大小并无显著变化。
图16
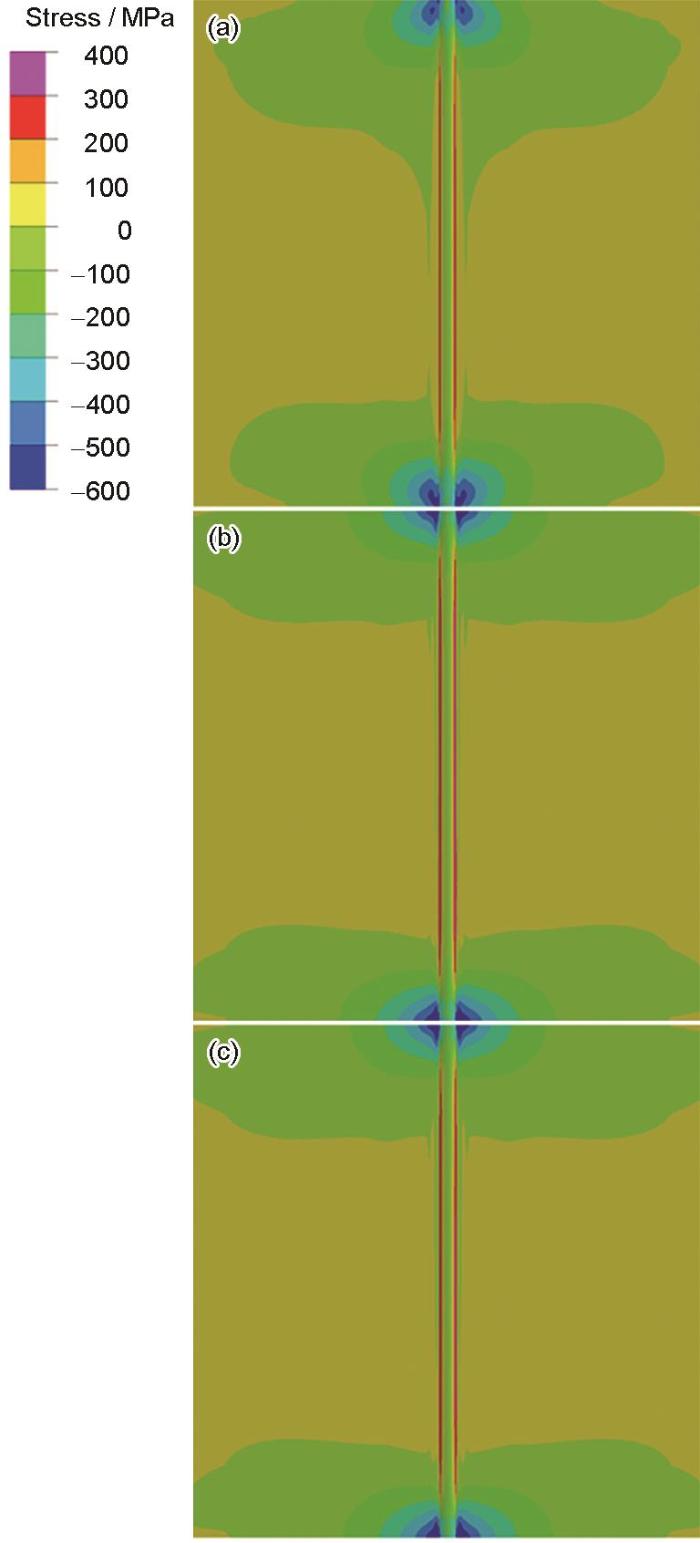
图16 超高强钢对接接头3种计算案例的上表面横向残余应力云图
Fig.16 Distributions of welding residual stresses of top surface at transversal direction under case A (a), case B (b), and case C (c) of UHSS butt joint
图17为3种计算案例的中央断面横向残余应力分布云图。3种计算案例的中央断面横向残余应力云图相比较没有显著差异,在上、下表面焊缝两侧的焊趾处均有较大的拉伸横向残余应力,同时在焊缝填充金属中的上表面以及两侧有相对较大的压应力,其余部分的应力分布相对平缓,而且应力的绝对值不大。总体上,由于焊件在纵向的拘束大,而在横向的拘束相对较小,对接接头的横向残余应力在数值上要明显低于纵向残余应力。
图17
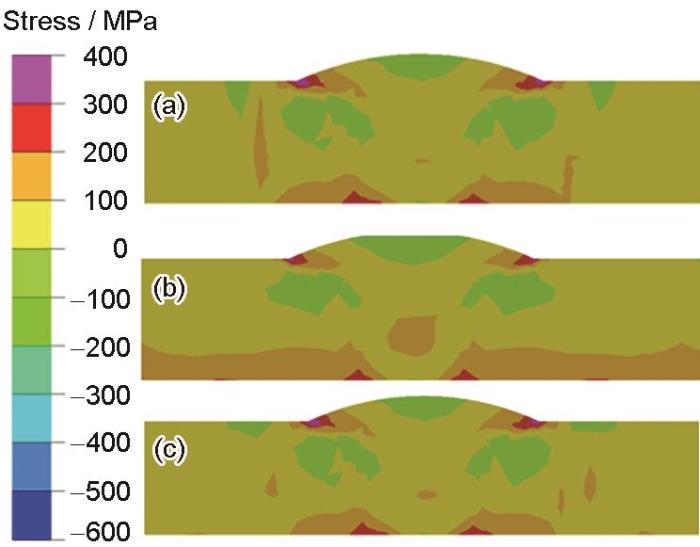
图17 超高强钢对接接头3种计算案例的中央断面横向残余应力云图
Fig.17 Distributions of welding residual stresses of central section at transversal direction under case A (a), case B (b), and case C (c) of UHSS butt joint
图18是3种计算案例中央断面上表面的横向残余应力分布计算结果与盲孔法测量结果的对比图。从图可以看出,与纵向残余应力分布相比,3种计算案例的横向残余应力分布差异不大,不同案例各个位置横向残余应力最大差值位于距焊缝中心6.5 mm位置,其值为138 MPa (图18a)。焊缝区域横向残余应力的分布没有差异,但热影响区横向残余应力峰值相对比,Case A、Case B和Case C呈现出递增的趋势,Case C的横向残余应力峰值为406 MPa (图18b)。与Case A相比,Case B在热影响区横向残余应力分布上也发生了较显著的变化,在距焊缝中心7~10 mm范围内,横向残余应力由拉伸应力转变为压缩应力,随着离焊缝的距离逐渐增加,Case A和Case B的横向残余应力逐渐趋近。与Case B相比,Case C在横向残余应力分布上没有显著的变化,热影响区横向压缩残余应力较Case B略有增加,但差异不大。
图18
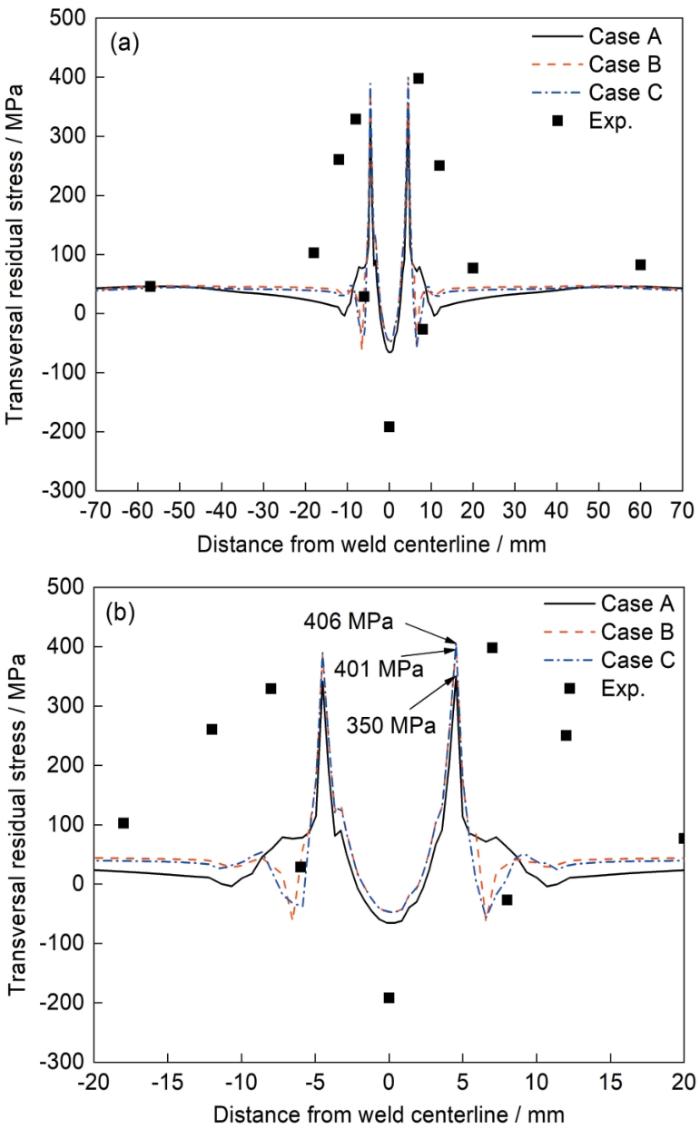
图18 超高强钢对接接头3种计算案例的中央断面上表面横向应力分布计算结果与实验测量结果对比
Fig.18 Comparisons of transversal welding residual stresses along center line of the top surface cross-section between computational and experimental results (a) and local magnified curves (b) under case A, case B, and case C of UHSS butt joint
从3种计算案例横向残余应力分布计算结果与实验测量结果的对比中可以看出,计算结果与实验测量结果存在一定的差异,其原因可能与盲孔法测量残余应力的方法有关:一方面,焊前对应变片粘贴位置的打磨会引入一定程度的塑性应变;另一方面,当盲孔法测残余应力所用的钻头钻速较低时,在钻孔过程中容易引起一定的孔边塑性变形,导致测得的残余应力偏高。总体来说,Case C的计算结果与实验测量结果最为吻合。
4 结论
(1) 1600 MPa级超高强淬火钢母材的平均显微硬度为520 HV,板厚为5 mm的单道焊对接接头的热影响区显微硬度最高值为541 HV,软化区显微硬度最低值为320 HV,软化区宽度约16 mm。焊接热循环对热影响区硬度有一定程度影响,对软化区的硬度有显著影响。
(2) 固态相变对纵向残余应力的大小和分布有较显著的影响。固态相变会使热影响区的纵向残余应力显著降低,纵向残余应力峰值不是出现在热影响区而是在紧邻热影响区的母材上,在不考虑软化的情况下纵向残余应力峰值达到1339 MPa。固态相变对横向残余应力的大小和分布有一定的影响,在考虑固态相变的情况下,横向残余应力的峰值与不考虑固态相变情况相比有一定幅度增加。
(3) 数值模拟结果表明,软化效应对纵向残余应力的分布形态几乎没有影响,但是软化区的纵向残余应力有一定幅度的降低,在紧邻热影响区的母材上的应力峰值为1032 MPa,与不考虑软化效应的计算结果相比,下降了307 MPa。软化效应对横向残余应力的分布形态没有影响,横向残余应力值略有增加,但整体差异不大。横向残余应力的峰值为406 MPa,远小于母材的常温屈服强度。
(4) 数值模拟结果与实验结果比较可知,在同时考虑固态相变和软化效应的情况下,超高强钢平板对接接头焊接残余应力的计算结果与实验值吻合最好,验证了本工作所开发的同时考虑“固态相变”与“软化效应”材料模型的妥当性。
来源:金属学报






