分享：基于核偏最小二乘法的板形过程监测

北京首钢冷轧薄板有限公司，北京　101304

摘要: 随着时代的发展和科技的进步，各行各业对于板材的质量和产量有了更高的要求。在实际应用中，大多数系统的内部机理十分复杂，传统的机理模型已无法满足对系统内部参数进行分析、表达。本文基于偏最小二乘法（PLS）提出一种核偏最小二乘法（KPLS）的板形过程监测方法，结果表明KPLS模型平均故障检测率为96.42%，误报率为10.14%，说明该方法用于板形的过程监测具有可行性。

近年来国内生产总值逐步上升，人民对美好生活的向往也逐渐增加，这就对产品质量提出了更高的要求。板形在冷轧领域直接影响了产品的品质和产量。近年来我国冷轧产业虽然得到了大幅提升，但与西方发达国家还有诸多差距。在实际的生产过程中不仅有钢材自身的组成成分还有轧机运行时的各种条件对板形具有重大影响[1]，但是这样复杂系统的内部机理几乎无法使用机理模型来进行描述。而现在随着数据存储和分析技术的大幅提升，采用数据来进行驱动的非机理式模型能很好地对板形过程进行监测[2-3]。

偏最小二乘法（Partial least squares，PLS）采取非线性迭代偏最小二乘（NIPALS）算法将整个过程变量空间分解为两部分，一部分为与质量变量有关的主元空间，另一部分则是残差空间。这种算法在复杂工业过程的监测和建模中取得了较好的应用效果。基于此本文提出一种基于核偏最小二乘法的板形过程监测方法。

1.   板形缺陷

直观上说板形是描述板带材形状的一个综合性概念，板形缺陷是指钢材在现代轧制生产中及生产后的产品中出现的翘曲以及横向厚度的残差的总称。板形缺陷的本质就是板带材生产过程后内部出现了残余应力的不均匀分布，这些不均匀分布的残余应力会导致板形缺陷的产生[4]。板形缺陷在表征上又主要分为两种，一种是“隐含”的板形不良，另一种是“表现”的板形不良。“隐含”的板形不良是因为残余应力存在，但不能在产品表面直观地表现为板带翘曲，如图1所示；而“表现”的板形不良是因为残余应力存在，并能够在产品表面直观地表现为板带翘曲，如图2所示[5]。

图  1  “隐含”板形不良

下载: 全尺寸图片 幻灯片

图  2  “表现”板形缺陷

下载: 全尺寸图片 幻灯片

在板带材轧制过程中，板形受多种因素共同作用，其中包括板带材自身的物理特性和形状因素，因为其会直接影响轧制力大小，进而直接影响板形。而轧制因素对板形的影响更为复杂，例如轧制压力、轧制速度、温度、摩擦、张力、弯辊力以及轧辊间接触应力分布等都会对板形产生直接或间接的影响[6]。

要想评价板形的好坏需要为板形设置一个量化指标，既可以在生产中对板带材的质量进行评判，也可以系统地开展对板形控制的探索。

通过计算平直部分的基准长度与波浪部分曲线长度的相对长度差来作为指标。由于这部分十分微小，为了便于开展研究，国内外常用IU来作为这部分差值的单位，通常一个IU表示相对长度差为10−5${10}^{-5}$[7]。

2.   核偏最小二乘法介绍

2.1   偏最小二乘法原理

偏最小二乘法是以主元分析法（Principle component analysis，PCA）为核心的投影降维方法。但相比于PCA，PLS能更加清晰地表达出过程变量和质量变量之间的关系，并可以通过观察过程变量的变化情况来监测质量指标的异常与否[8]。

假设对某生产过程的m$?$个过程变量和p$?$个质量变量进行n$?$次采样，得到过程变量矩阵X$\mathit{?}$和质量变量矩阵Y$\mathit{?}$，基于PLS模型的方法将数据矩阵[X,Y]$\left[\mathit{?},\mathit{?}\right]$投影到一个由较少潜变量[t1,...,tA]$\left[{?}_1,...,{?}_{?}\right]$（A$?$为PLS主元个数）构成的低维空间中，其外部模型如式（1）所示。

式中，T=[t1,...,tA]$\mathit{?}=\left[{?}_1,...,{?}_{?}\right]$为得分矩阵，P=[p1,...,pA]$\mathit{?}=\left[{?}_1,...,{?}_{?}\right]$和Q=[q1,...,qA]$\mathit{?}=\left[{?}_1,...,{?}_{?}\right]$分别为X$\mathit{?}$和Y$\mathit{?}$的载荷矩阵，E$\mathit{?}$和F$\mathit{?}$分别为X$\mathit{?}$和Y$\mathit{?}$的残差矩阵。

PLS法将整个过程变量空间分为了两个投影方向的子空间：主元空间，即与质量相关因素空间；残差空间，即与质量无关因素空间。

2.2   核偏最小二乘法算法

基于Cover理论Rosipal等[9]提出了KPLS算法，其原理为：首先将原始输入数据通过非线性映射到高维的特征空间后再采取传统PLS算法计算新特征空间与所求质量数据之间的关系。

通过设定非线性映射函数?$?$，它能够将样本xi(i=1,2,...,N)${?}_{?}\left(?=1,2,...,?\right)$从原始变量空间映射到特征空间F，即

式中，特征空间F$?$的维数M$?$可以任意大甚至可能是无穷维。矩阵X$\mathit{?}$则映射为特征空间中的矩阵F$\mathit{?}$：

KPLS要求对Φ$\mathit{?}$进行零均值处理，首先求取?(xi)$?\left({?}_{?}\right)$的平均值?¯¯¯$\overline{?}$：

式中，IN=[11⋅⋅⋅1]T∈RN${\mathit{?}}_{?}={\left[\begin{array}{cccc}1& 1& \cdot \cdot \cdot & 1\end{array}\right]}^{\text{T}}\in {\mathbf{?}}^{?}$，然后求取零均值的Φ¯¯¯¯$\overline{\mathit{?}}$：

因此，非线性数据(X,Y)$\left(\mathit{?},\mathit{?}\right)$被映射为线性数据(Φ¯¯¯¯,Y)$\left(\overline{\mathit{?}},\mathit{?}\right)$。然后利用PLS算法构建Φ¯¯¯¯$\overline{\mathit{?}}$和Y$\mathit{?}$之间的KPLS模型：

式中，T∈RN×γ$\mathit{?}\in {\mathbf{?}}^{?\times ?}$称为得分矩阵，P∈RM×γ$\mathit{?}\in {\mathbf{?}}^{?\times ?}$是Φ¯¯¯¯$\overline{\mathit{?}}$的负载矩阵，Q∈Rl×γ$\mathit{?}\in {\mathbf{?}}^{?\times ?}$是Y$\mathit{?}$的负载矩阵， Φ¯¯¯¯r${\overline{\mathit{?}}}_{?}$和Yr${\mathit{?}}_{?}$分别是Φ¯¯¯¯$\overline{\mathit{?}}$和Y$\mathit{?}$的残差矩阵，γ$?$为潜变量个数。

根据Mercer定理，如果核函数是一个连续的核积分算子则存在由原始参数空间到以核函数作为内积的高维空间的映射。基于此，所选择的核函数必须要满足Mercer定理。有三种应用较为广泛的核函数：

（1）多项式核

（2）Sigmoid核

（3）高斯核

核参数需要根据先验知识确定。其中多项式核和高斯核一定满足Mercer定理，而Sigmoid核只有部分情况下才满足。需要特别提出的是核参数的取值是故障检测的重要因素，不同的核参数得到的故障检测结果可能大相径庭[10]。

2.3   核偏最小二乘法监测模型

在KPLS的主成分空间和残差空间分别使用T2${?}^2$统计量和SPE统计量进行监控。对在线样本xnew${?}_{\text{new}}$映射为?(xnew)$?\left({?}_{\text{new}}\right)$并进行零均值处理后为?¯(xnew)$\overline{?}\left({?}_{\text{new}}\right)$，则可知：

式中，tnew∈Rγ${\mathit{?}}_{\text{new}}\in {\mathbf{?}}^{?}$为样本?¯(xnew)$\overline{?}\left({?}_{\text{new}}\right)$的得分。因此，KPLS主成分子空间的T2${?}^2$统计量为：

对应阈值为：

KPLS残差子空间的SPE统计量为：

对应阈值为：

式中，参数g和h通过训练样本根据如下公式计算：

2.4   核偏最小二乘法板形过程监测结果

采用某月生产的钢种为CR780Y980T-CP厚度为1200~1500 mm、宽度为1.3~1.6 mm，浪形标记全部为复合浪，共计11卷。在本次建模中，板形均值小于3视为正常样本，取8卷中板形均值小于3的作为训练集，其余3卷作为测试集，对数据进行下采样，采样频率为200 ms，选择‘FLC5-F5_flatness_error’（板形偏差）作为待建模数据，在对数据进行标准化处理后进行建模和监测。

从表1中可以看出所有测试结果的故障检测率均在93%以上，误报率在16%以下，平均故障检测率为96.42%，误报率为10.14%。

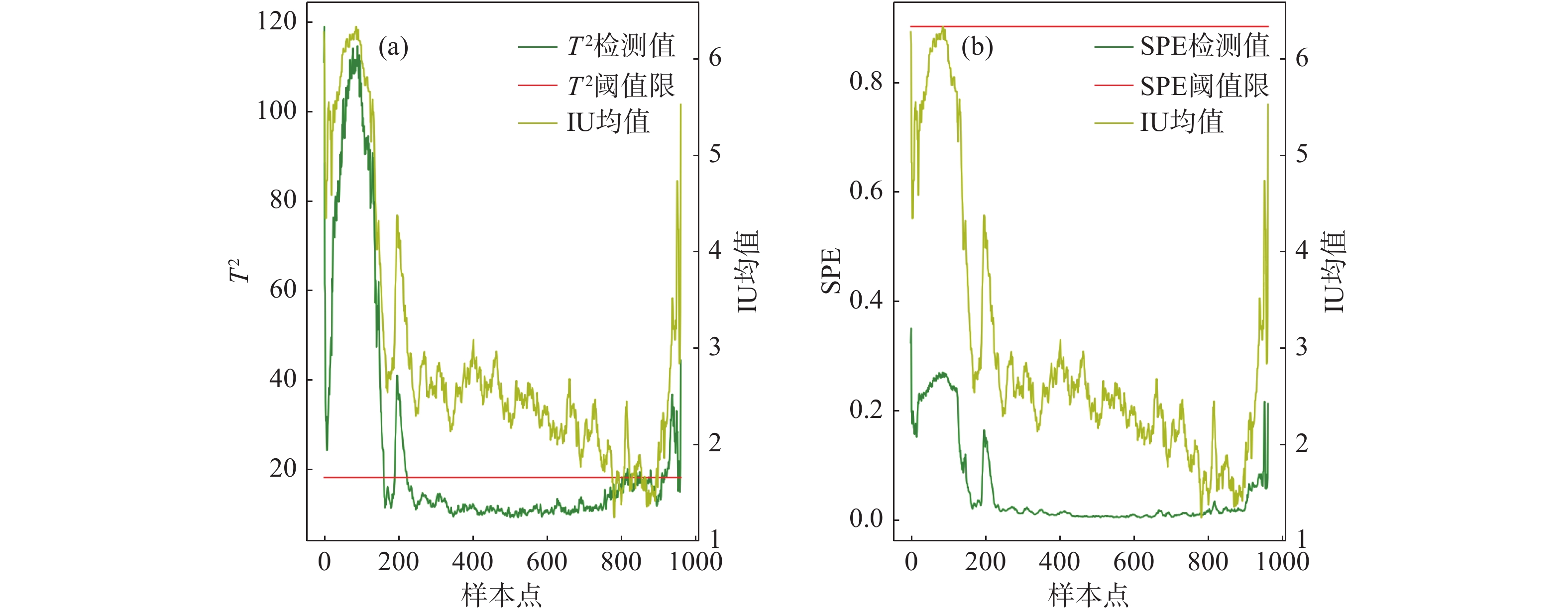
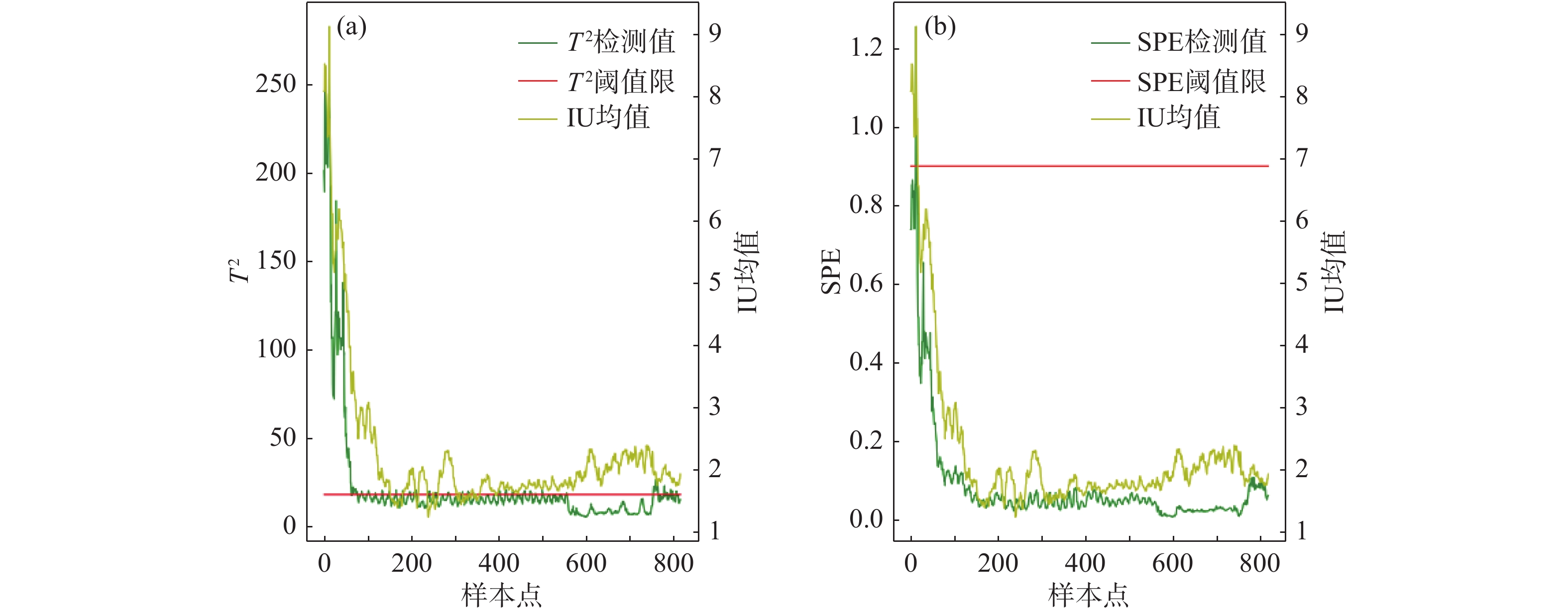
表  1  核偏最小二乘法过程监测故障检测率与误报率

钢卷号	故障检测率/%	误报率/%
HB19714404500	97.30	5.28
HB19811300100	93.04	15.88
HB19812605900	94.14	9.61
HB19B14704000	98.85	4.59
HB19B15902800	98.73	15.33
平均值	96.42	10.14

下载: 导出CSV 

| 显示表格

图3为卷钢HB19714404500统计图，其经过下采样所得所有采样点的故障检测率是97.30%，误报率是5.28%。图3（a）可以看出超出限值，表明KPLS模型在主元空间检测到了异常，即模型认为是主元空间的异常导致了IU的波动，图3（b）未超出限值，表明KPLS模型认为这卷钢中一些噪声或者小的波动不会引起IU波动。

图  3  卷钢号HB19714404500统计图:(a) T2统计量；（b）SPE统计量

下载: 全尺寸图片 幻灯片

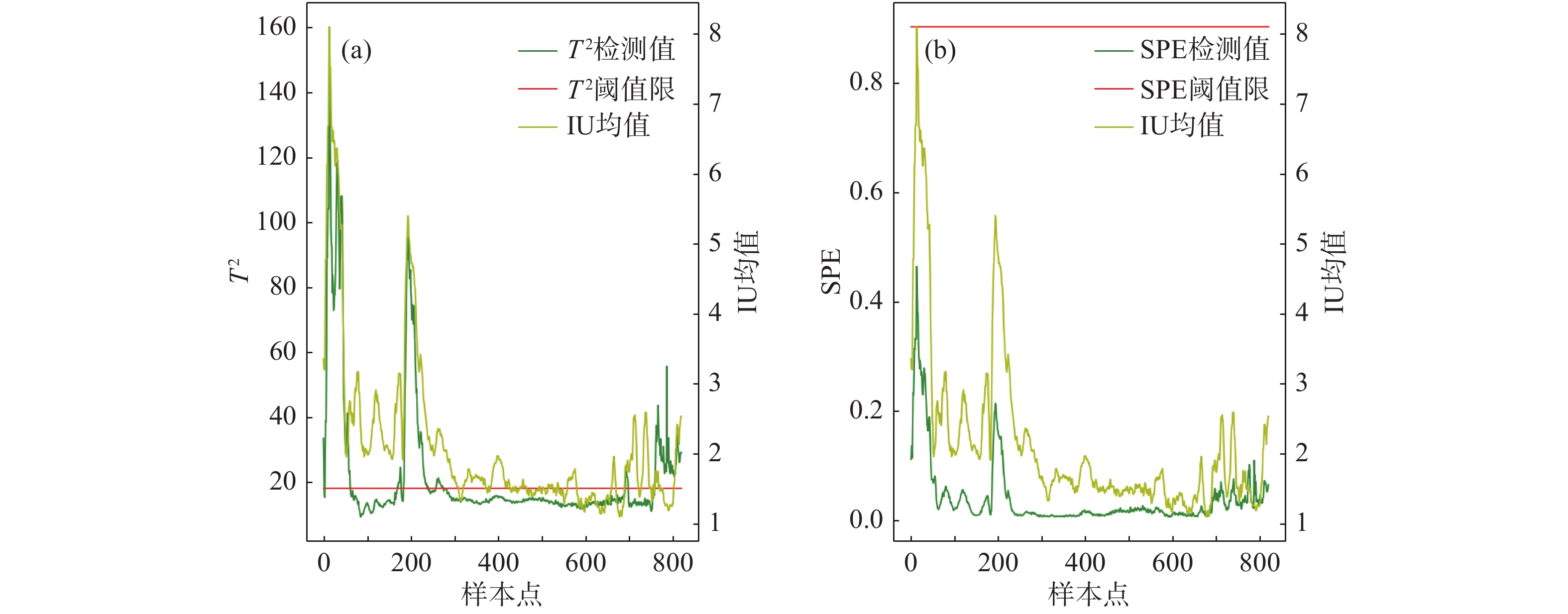
图4为卷钢HB19811300100统计图，其经过下采样所得所有采样点的故障检测率是93.04%，误报率是15.88%。图4（a）可以看出超出限值，表明KPLS模型在主元空间检测到了异常，即模型认为是主元空间的异常导致了IU的波动，图4（b）未超出限值，表明KPLS模型认为这卷钢中一些噪声或者小的波动不会引起IU波动。

图  4  卷钢号HB19811300100统计图:(a) T2统计量；（b）SPE统计量

下载: 全尺寸图片 幻灯片

图5为卷钢HB19812605900统计图，其经过下采样所得所有采样点的故障检测率是94.14%，误报率是9.61%。图5（a）可以看出超出限值，表明KPLS模型在主元空间检测到了异常，即模型认为是主元空间的异常导致了IU的波动，图5（b）未超出，表明KPLS模型认为这卷钢中一些噪声或者小的波动不会引起IU波动。

图  5  卷钢号HB19812605900统计图:(a) T2统计量；（b）SPE统计量

下载: 全尺寸图片 幻灯片

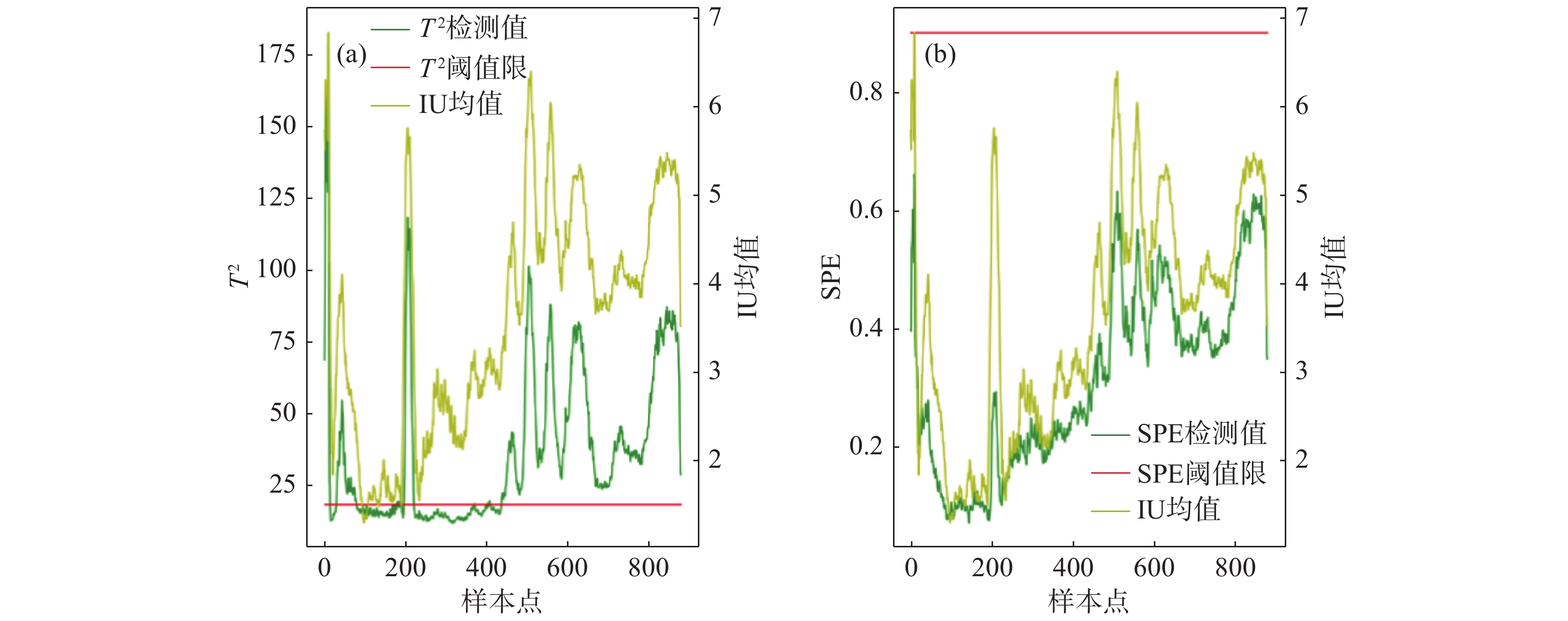
图6为卷钢HB19B14704000统计图，其经过下采样所得所有采样点的故障检测率是98.85%误报率是4.59%。图6（a）可以看出超出限值，表明KPLS模型在主元空间检测到了异常，即模型认为是主元空间的异常导致了IU的波动，图6（b）部分超出说明KPLS模型认为这卷钢中部分噪声或者小的波动引起了IU波动。

图  6  卷钢号HB19B14704000统计图:(a) T2统计量；（b）SPE统计量

下载: 全尺寸图片 幻灯片

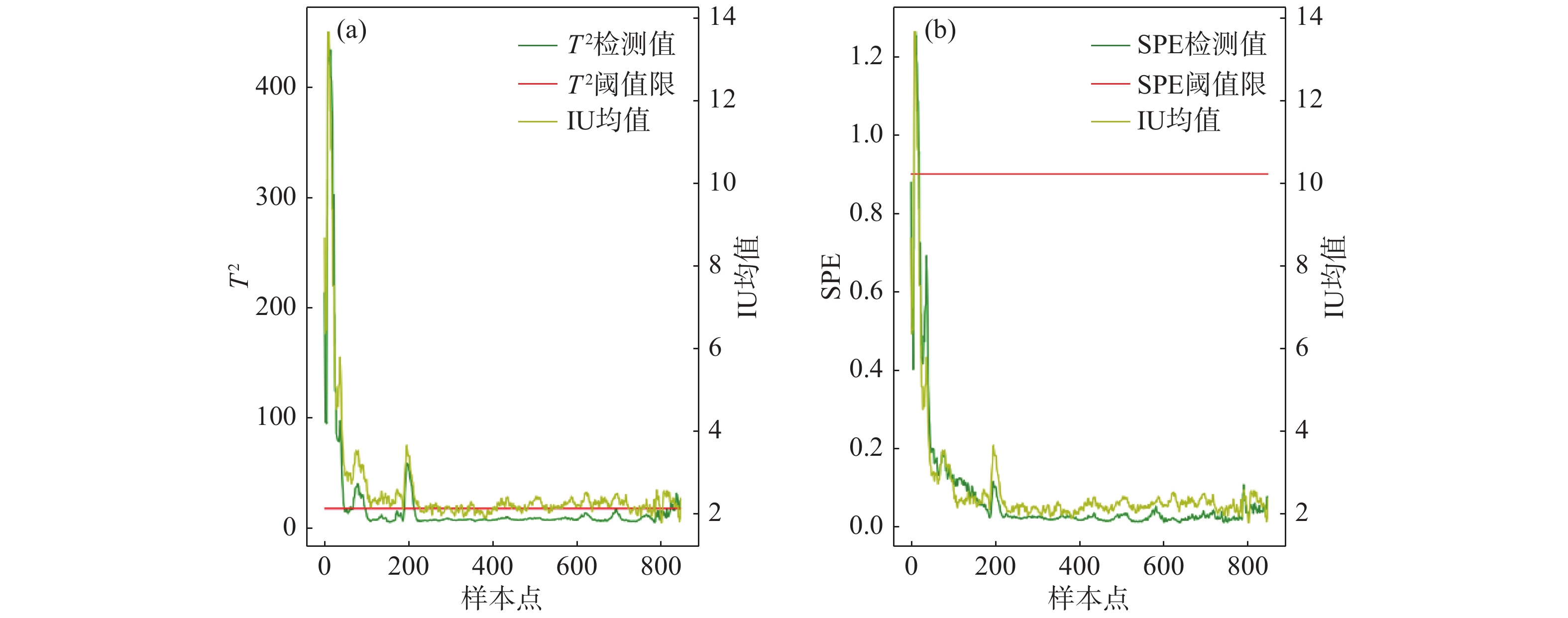
图7为卷钢HB19B15902800统计图，其经过下采样所得所有采样点的故障检测率是98.73%，误报率是15.33%。图7（a）可以看出超出限值，表明KPLS模型在主元空间检测到了异常，即模型认为是主元空间的异常导致了IU的波动，图7（b）部分超出说明KPLS模型认为这卷钢中部分噪声或者小的波动引起了IU波动。

图  7  卷钢号HB19B15902800统计图:(a) T2统计量；（b）SPE统计量

下载: 全尺寸图片 幻灯片

3.   结束语

本文介绍了PLS法和KPLS法的回归模型和过程监测模型，提出了核偏最小二乘法诊断模型用于非线性模型诊断中板形的监测。KPLS模型能够监测到IU值的变化，验证了模型的正确性。与传统PLS模型相比，KPLS模型能够有效地提高故障检测率和降低误报率。KPLS模型对测试数据的诊断结果表明KPLS模型平均故障检测率为96.42%，误报率为10.14%，对于一些工况能够起到较好的监测效果，可以对该模型进一步深究探讨，通过该模型分类出不同工况并针对这些工况具体分析。