分享:W-Ni-Fe三元合金等离子球化过程的SPH仿真研究
1.
2.
3.
针对表面张力影响下的W-Ni-Fe三元合金,通过光滑粒子流体动力学(SPH)建立了仿真多元金属液滴碰撞融合过程的数值模型,获得了流体在等离子球化过程中的流场和温度分布。结果表明,W的占比越高、粒径越小、环境温度越高、Marangoni力越大,则球化度越好。根据SPH模拟结果选择了平均粒径1.5 μm的W粉、平均粒径4.1 μm的Ni粉和平均粒径2.4 μm的Fe粉为原料,按照质量比W∶Ni∶Fe=90∶7∶3进行喷雾造粒,在等离子焰流温度为8000℃条件下球化,球化后的三元合金粉末球形度好,内部致密。球化后颗粒流动性为11.62 s/50 g,松装密度10.66 g/cm3,有利于使用铺粉方法进行3D打印。证实了SPH仿真结果可靠,该模拟结果可用于指导难熔金属W的等离子球化制备工艺。
关键词:
金属增材制造3D打印技术是制造业中正在迅速发展的一项新兴技术,被称为第三次工业革命的重要标志之一,在航空航天等高端装备用复杂构件制造中,3D打印具有突出的优势和广阔的应用前景[1]。金属3D打印技术的原材料以球形金属粉末为主,为获得均匀的铺粉和致密的打印显微组织,金属3D打印工艺要求原料粉末具有高纯度、高流动性和窄的粒径分布等特性[2]。与传统粉末相比,球形粉末具有更好的流动性、真实密度[3]和耐磨性[4],合成物精度更高、性能更佳[5]。W具有高熔点(3410℃)、高密度(19.35 g/cm3)、高硬度、高弹性模量等优异性能,在国防军工、航空航天和核工业等领域中有重要的作用[6]。目前,球形粉末的传统制备方法有还原法、电弧喷枪法、雾化法、喷雾干燥法等,但由于难熔金属高熔点、易氧化等特性,使用上述方法很难实现较高的球化率和球形度,极大限制了难熔金属球形粉末制备技术的发展[7]。
感应耦合等离子球形化工艺制备的球形粉体具有球化率高、纯度高、粒径分布均匀等优点。难熔金属粉末在等离子球化过程中,金属粉末比例、液滴温度、尺寸、表面张力等因素都对液滴融合过程和融合效果产生影响,因此有必要研究这些因素对融合过程的具体影响。随着计算机硬件和先进算法的发展,计算模拟已经成为研究极端条件下材料微观结构演化及性能分析的重要研究手段[8]。关于感应耦合等离子球化过程的建模,已有学者进行了相关研究。Nam等[9]通过有限元方法,对等离子球化过程中舱室内部的流场和温度场进行了分析,并根据结果对感应等离子体的设备参数进行了优化。该研究主要集中于金属粉末等离子球化过程中舱室内部的流场和温度场,而关于金属粉末在高温高速环境中熔化并碰撞融合的微观过程,则未见相关报道。Bernardi等[10]利用FLUENT流体计算软件,对电感耦合等离子体球化系统Ar气流场进行了数值模拟,采用离散颗粒群轨迹模型(DPM)模拟了注入的合金粉末的颗粒轨迹,预测了不同粒径粉末通过Ar气流场后的颗粒收集率。目前模拟流体常用的有限单元法、有限体积法等,都很难实现对液滴融合过程的模拟。
光滑粒子流体动力学(smoothed particle hydrodynamics,SPH)是一种基于粒子离散的无网格数值仿真方法,它基于粒子间的相互作用来模拟流体现象,且无网格,因此较适合模拟特殊的流动现象,如表面张力、液滴融合等。Morris[11]和Tong等[12]通过SPH方法,分别对单个液滴的表面张力及热毛细流进行了模拟。Russell等[13]使用SPH方法模拟球化后的金属粒子,对金属的激光增材过程进行了数值仿真,结果表明,将SPH方法用于模拟激光增材过程是可靠的。Zhang[14]使用SPH方法,对2个同种液滴以不同速率、不同方向碰撞融合的动态过程进行了模拟,并与基准测试结果进行比较,验证了SPH方法的可行性。
本工作采用SPH算法,利用数值模拟方法研究等离子球化过程的微观演变过程,探明钨合金球形粉末成形、预合金化及致密化机理。在模型中,研究了元素质量比、液滴温度、尺寸、表面张力等因素对液滴融合过程和融合效果的影响,研究结果有助于探索合金成分设计、喷雾干燥工艺、等离子球化工艺对球形度、合金化及致密化程度的影响,给出实验工艺的优化条件。
本工作的主要研究内容是异种金属液滴碰撞聚合时的流体流动过程,流动过程包含了多相流,其基本物理过程遵循描述流体流动过程的Navier-Stokes方程(N-S方程),对于考虑黏性力的不可压缩流体,有[15]:
式中,ρ为流体密度,kg/m3;u为流体的速度矢量,m/s;t为时间,s;p为压力,Pa;μ为动力黏度,Pa·s;I为单位矩阵;F为外部体积力,N/m3。
在多相流液滴碰撞聚合过程中,涉及的传热现象主要包括热传导及热对流,控制方程如下[15]:
式中,cp为材料的等压比热容,J/(kg·K);T为温度,K;λ为传热系数,W/(m2·K);
不同液滴的气液界面移动方程为[15]:
式中,?为界面变量;γ为重新初始化参数,m/s;εls为界面厚度控制参数,m。
为了求解式(
SPH方法使用核函数插值实现场变量的积分表示,同时基于核函数的光滑长度确定任意粒子的影响域,并计算任意两粒子间的相互作用力。因此,W的选取对于计算结果的可靠性非常重要。本工作选择如下五次样条核函数,以得到更好的稳定性、更高的计算精度和较小的紧支域[20]:
式中,αd是与模型空间维度相关的常数,对于一维、二维、三维问题,分别有αd=
对于空间位置r任意一个连续的光滑函数f(r),可将其表示为[21]:
式中,r'为以r坐标为圆心、光滑长度为半径的区域内所有非r点的位置矢量。
相应地,函数的导数可表示为[21]:
当求出粒子处的函数及其导数后,可使用
对上式进行粒子离散,可得粒子i处的场函数f(ri)及空间导数的表达式分别为[21]:
式中,ri、rj分别为粒子i、j的位置矢量,i、j=1、2、3;mj 为粒子j的质量,kg;ρj为粒子j的密度,kg/m3;Wij为粒子i的光滑函数在粒子j位置的值。
采用分部积分处理,可得到更精确的表达式[21]:
SPH法使用粒子离散求解如下流体动力学控制方程。
质量守恒方程[21]:
式中,ρi为粒子i的密度,kg/m3;
动量守恒方程[21]:
式中,
能量守恒方程[21]:
式中,ei为粒子i的内能,J;pi和pj分别为粒子i和j处的水静压力,Pa;
为了避免Lagrange粒子中出现的拉伸不稳定现象,Monaghan[22]在动量守恒方程和能量守恒方程中加入了人工黏性项,其表达式为[21]:
其中,
式中,∏ij为人工黏度;α∏和β∏为无量纲系数;ci和cj分别为粒子i和粒子j的声速,m/s;
在求解液体碰撞等问题时,可能会产生过热,为了解决这个问题,引入了人工热量项[21]:
其中,
式中,qi和qj分别是粒子i和粒子j处的速度散度型人工黏度;
这样,考虑了人工黏性项之后的动量方程表达式为[21]:
考虑了人工黏性项和人工热量之后的能量表达式为[21]:
本工作研究了3种金属液滴的碰撞融合过程,除了常规的流体动力学分析之外,还考虑了多相流、表面张力等物理过程。
在模拟多相流时,直接赋予每个粒子不同的材料参数,材料参数发生变化的位置,即为不同流体相之间的粒子边界,因此不需要专门对相界面进行跟踪。对于不可压缩流动,使用完全不可压缩SPH (truly incompressible SPH,ICSPH)模型对其进行模拟。ICSPH方法假设流体是完全不可压缩的,因此在计算时不使用状态方程。在ICSPH模型中,通过使用速度的零散度以及密度的零变分,以实现流体的完全不可压缩假设[23,24]。
在ICSPH模型中,粒子i的光滑函数χi(r)为[25]:
式中,Wi(r)是光滑核函数,σ(r)是粒子体积。
据此推导出粒子位置、速度更新的ICSPH粒子离散表达式为[25]:
式中,
在计算表面张力时,本工作使用了基于修正的光滑粒子方法(corrective smoothed particle method,CSPM),该方法能提高计算曲率时的精度,从而避免传统基于表面力(continuum surface force,CSF)模型计算表面张力时的缺点[25]。
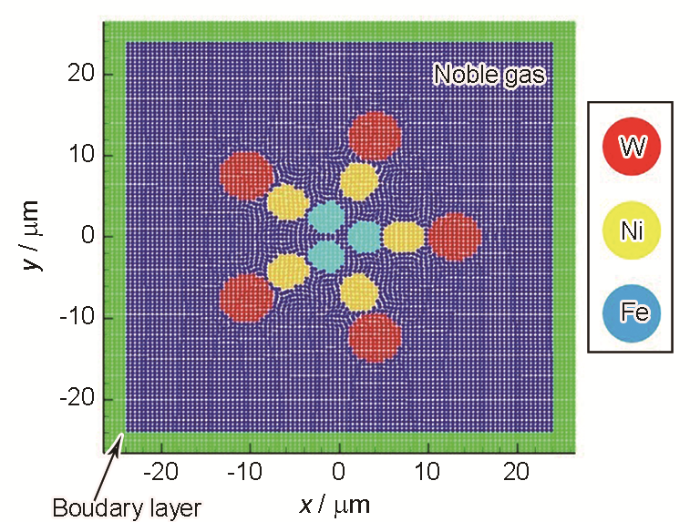
模拟了三元合金W-Ni-Fe的金属粉末球化过程,并建立如图1所示的二维SPH粒子模型,其中液滴粒子数为302,惰性气体粒子数为1858,边界层粒子数为300。W液滴半径可变,Ni液滴、Fe液滴半径固定为2 μm。粒子间距为1 μm,边界层厚度为2 μm,粒子初始碰撞速率为2 m/s。
图1 W-Ni-Fe三元合金光滑粒子流体动力学(SPH)模型
Fig.1 Schematic of smoothed particle hydrodynamics (SPH) model for W-Ni-Fe ternary alloy
液滴融合模拟包括3种元素配比(W∶Ni∶Fe质量比=90∶7∶3、85∶10.5∶4.5和80∶14∶6)、3种环境温度(5000、8000和10000℃)、3种液滴尺寸(2.5、3.0和3.5 μm)、3种Marangoni系数(0.058、0.58和5.8)情况,共12种工况。模型中使用的材料性能参数如表1所示,具体的工况参数如表2所示。
表1 材料物性参数
Table1
表2 不同工况的建模参数
Table 2
在模拟开始前,先进行模型的可行性验证。如图2是SPH计算方法得到的不同条件下液滴碰撞结果分布。该结果与Qian和Law[26]实验得到的结果基本一致,但本工作得到的分布图中没有出现“反弹”碰撞现象。这是由于Qian和Law[26]是在真实的三维环境中做实验,而“三维”液滴碰撞后在接触区域内会有气体进入,形成“气体空穴”,“空穴”内的气体受到挤压,压力增大,在气体压力的作用下液滴出现反弹分离;但在“二维”数值模拟中,由于不存在第三维空间,在二维平面上液滴碰撞接触的区域,不会出现“气体空穴”,因此未出现“反弹”的碰撞结果。
图2 利用SPH方法计算的不同条件下液滴碰撞模拟结果分布图
Fig.2 Simulation results under different collision conditions by using SPH
图3是W-Ni-Fe三元合金在3种元素配比下液滴的融合状态。可以看出,W∶Ni∶Fe为90∶7∶3的工况,在1~3 ms内完成了液滴的凝聚、分离、融合的过程,由于W的粒径比其他2种金属大,在融合过程中不容易发生分离,故导致W粒子包裹在整体颗粒的外侧,与其他粒子融合度不高,因此存在非常明显的属于异种金属颗粒的边界。对于W∶Ni∶Fe为85∶10.5∶4.5的工况,在5 ms时间内,仍未有效融合,球体中间还有明显的气泡。这是由于在这种配比条件下,Ni的颗粒数比较高,且分布在中间位置。而Ni的表面张力系数相对较大,较其他的金属颗粒更不容易分离,故造成Ni颗粒像围栏一样,阻断了外面的W颗粒和里面的Fe颗粒的融合,使得内部Ni-Fe颗粒形成的空气带无法被快速填充,于是出现中间充斥大气泡的现象。但随着时间的延长,这种现象会随金属液滴的融合而消失。当W∶Ni∶Fe为80∶14∶6的组合时,在相同时间下,球化水平最低。但是这无法说明W的质量占比高或者低对于实际球化效果的影响,较大可能是由于初始粒子个数和空间排布对3种金属融合的效果产生了影响。6个W粒子结构的对称性要远好于后2种工况下5个W粒子的结构,故更容易在短时间内融合为一个近似球体。其他非完美对称结构则需要更长时间实现去梯度带来的自我平衡。根据现有计算结果可知,在相同时间内,W占比越大越有利于球化。
图3 W-Ni-Fe三元合金在不同元素配比下(模型1~3)的液滴融合状态
(a) W∶Ni∶Fe=90∶7∶3 (b) W∶Ni∶Fe=85∶10.5∶4.5 (c) W∶Ni∶Fe=80∶14∶6
Fig.3 Simulation results for W-Ni-Fe ternary alloy after droplet fusion under different mass ratios of W∶Ni∶Fe (models 1-3)
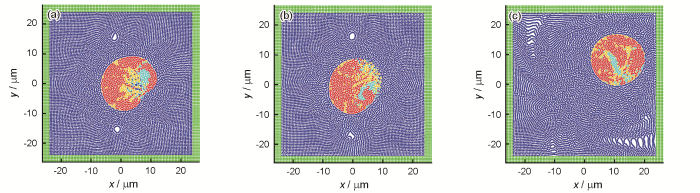
图4是W-Ni-Fe三元合金在3种温度(模型4~6)时的液滴融合状态。可以看出,在相同时间内,温度越高,颗粒动能越大,球化程度越高。在5000℃条件下,粒子动能较小,液滴未能充分实现分离和融合就已成型,3种金属的融合均匀性稍差。升温后,粒子的运动速率和液滴的分离速率均相对较快,导致球体表面的速度梯度较大,进一步造成了整体过程的不平衡性。而球化过程的好坏,往往取决于达到动态平衡的快慢。
图4 W-Ni-Fe三元合金在不同温度下(模型4~6)的液滴融合状态
(a) 5000oC (b) 8000oC (c) 10000oC
Fig.4 Simulation results for W-Ni-Fe ternary alloy after droplet fusion under different temperatures (models 4-6)
图5是W-Ni-Fe三元合金在Ni、Fe液滴半径不变,3种不同W液滴半径(模型7~9)时液滴融合的状态。可以看出,3种情况球化结果基本一致,同时发现,当W粉粒径逐渐缩小时,合金球化过程中气孔也随之减少。
图5 W-Ni-Fe三元合金在不同W液滴直径下(模型7~9)的液滴融合状态
(a) 2.5 μm (b) 3.0 μm (c) 3.5 μm
Fig.5 Simulation results for W-Ni-Fe ternary alloy after droplet fusion under different diameters of W (models 7-9)
图6是W-Ni-Fe三元合金在不同Marangoni系数(模型10~12)时的液滴融合状态。可以看出,在相同时间内,Marangoni力越大球化程度越好,因为Marangoni力可以让由表面张力梯度引起的切向运动速率更快。
图6 W-Ni-Fe三元合金在不同Marangoni系数(模型10~12)时的液滴融合状态
(a) 0.058 (b) 0.58 (c) 5.8
Fig.6 Simulation results for W-Ni-Fe ternary alloy after droplet fusion under different Marangoni coefficients (models 10-12)
表3列出了W-Ni-Fe三元合金不同条件时融合后的球化度及致密度。图7根据表3中的数据分别拟合出了球化度和致密度随元素配比、温度、粒径、Marangoni系数的变化曲线,并通过内插方式得出了一些关键参数点上的球化度和致密度数据。由表3可知:(1) 对于不同配比时,图7a中W的配比越低,合金的球化度越低,当W∶Ni∶Fe=85∶10.5∶4.5,W的占比约为85%时,合金的致密度最低;(2) 对于不同温度时,随着温度的升高,合金的致密度越高,而球化度在温度增加到约7250℃时最低,进一步升高温度,球化度则迅速增加,由此可见高温有助于提高此合金的融合效率;(3) 对于不同粒径时,致密度和球化度呈现完全相反的变化规律,当粒径约为3.25 μm时,致密度达到最低值,球化度达到最高;(4) 对于不同Marangoni系数时,随着系数的增大,合金的球化度和致密度都在稳步增大,可见Marangoni系数越大,对W-Ni-Fe合金的融合越有利。
表3 不同条件下W-Ni-Fe三元合金的融合数据
Table 3
图7 不同条件下液滴融合后的球化度及致密度曲线
(a) models 1-3 (b) models 4-6 (c) models 7-9 (d) models 10-12
Fig.7 The spheroidization ratio and compactness curves obtained by an interpolation method
通过上述模拟仿真结果的分析,选择验证实验的具体参数为:W粉平均粒径1.5 μm,Ni粉平均粒径4.1 μm,Fe粉平均粒径2.4 μm;W粉、Ni粉与Fe粉质量比90∶7∶3,等离子球化温度8000℃。使用Tek-15 kW感应耦合等离子球化设备进行实验,等离子焰流温度可调整范围5000~15000℃,熔融颗粒在表面张力作用下收缩,最终为球形[27]。使用SU5000扫描电镜(SEM)对W-Ni-Fe三元合金粉末进行球化前后形貌进行对比分析,观察合金粉末形貌的变化,验证实验球化结果。通过能谱(EDS)对球化后W-Ni-Fe三元合金颗粒进行成分分析,观察3种金属球化后均匀分布情况,了解颗粒内部致密度,是否存在大量气孔。
原始W粉、Ni粉和Fe粉粒度过细,流动性弱,无法顺畅通过等离子球化送粉系统进行球化,所以必须通过喷雾干燥方式造粒,才能够实现3种粉末均匀分布,具备一定流动性能。造粒完成后W-Ni-Fe的SEM像如图8a所示。球化后得到的三元合金粉末球形度较高,如图8b所示。球化后颗粒流动性能为11.62 s/50 g,松装密度为10.66 g/cm3,这2项指标在3D打印中具有非常好的综合性能优势[28]。
图 8 W-Ni-Fe三元合金球化前后的SEM像
Fig.8 SEM images of W-Ni-Fe ternary alloy before (a) and after (b) spheroidization
选取球化后的合金粉末进行剖面分析,如图9所示。可以看到,经过等离子球化后的W-Ni-Fe颗粒内部十分致密,3种金属元素分布均匀,无明显气孔存在,与模拟仿真结果基本一致。
图9 W-Ni-Fe三元合金球化后的SEM像和EDS分析
Fig.9 SEM image and corresponding EDS analyses for W-Ni-Fe ternary alloy after spheroidization
基于SPH方法,建立了W-Ni-Fe三元合金颗粒等离子球化过程的数值模型,并模拟了其碰撞融合的动态过程。借助CSPM方法,模拟了相互碰撞的液滴,在表面张力作用下相互融合过程中的界面演化行为。液滴碰撞后,形成的较大液滴会在表面张力的作用下不断变化,最终趋于稳定形成球形,通过对比球化度和致密度2个特征参量评估球化合金颗粒的质量。当W的占比越高、W的粒径越小、环境温度越高、Marangoni力越大,则球化度越好。最后选择W粉平均粒径1.5 μm,Ni粉平均粒径4.1 μm,Fe粉平均粒径2.4 μm,按照质量比W∶Ni∶Fe=90∶7∶3进行混合,球化温度选择8000℃,球化后的三元合金粉末球形度好,内部致密,与模拟结果基本一致。球化后颗粒流动性能为11.62 s/50 g,松装密度为10.66 g/cm3,有利于铺粉方式进行3D打印。模拟结果可用于指导难熔金属W的等离子球化制备工艺。
1 物理过程数学模型
2 数值求解算法
2.1 粒子离散
2.2 求解运动方程
2.3 多相流及表面张力算法理论
3 模拟结果分析与验证实验
3.1 模拟结果与分析
图1
Element
Density
Viscosity
Thermal conductivity
Surface tension coefficient
Specific heat capacity
103 kg·m-3
10-3 Pa·s
W·m-1·K-1
N·m-1
J·kg-1·K-1
Fe
7.8
6.4
40.0
2.04
460
Ni
8.9
6.0
90.7
3.10
447
W
19.3
6.5
91.3
2.50
466
Model
Mass ratio of W∶Ni∶Fe
Temperature
Diameter of W
Marangoni coefficient
oC
μm
1
90∶7∶3
5000
3.0
5.8
2
85∶10.5∶4.5
3
80∶14∶6
4
90∶7∶3
5000
3.0
5.8
5
8000
6
10000
7
90∶7∶3
5000
2.5
5.8
8
3.0
9
3.5
10
90∶7∶3
5000
3.0
0.058
11
0.58
12
5.8
图2
图3
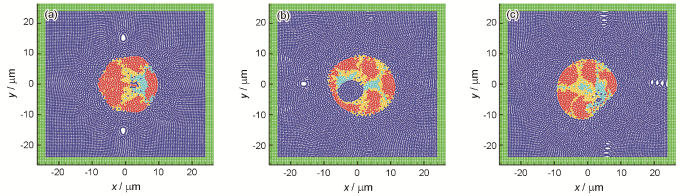
图4
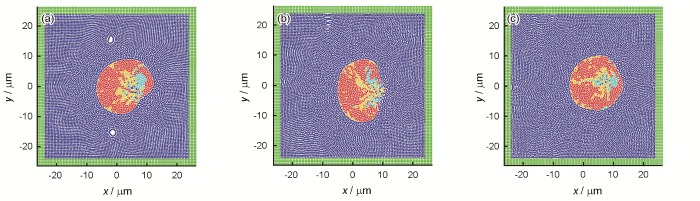
图5
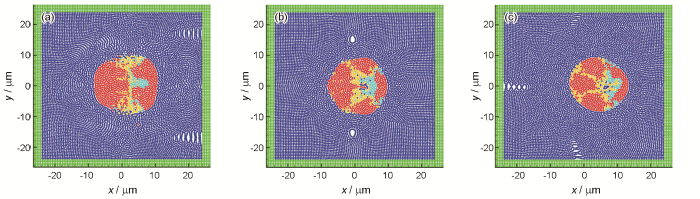
图6
Model
Spheroidization ratio
Compactness
1
89.37%
96.35%
2
85.64%
80.08%
3
82.75%
97.85%
4
81.34%
96.85%
5
70.71%
97.97%
6
90.34%
98.58%
7
80.33%
98.71%
8
89.37%
96.35%
9
85.26%
97.65%
10
79.01%
96.85%
11
86.61%
97.66%
12
95.26%
100.00%
图7

3.2 验证实验
图 8

图9

4 结论
来源--金属学报







 沪公网安备31011202020290号
沪公网安备31011202020290号
