分享:石墨烯纳米片增强镁基复合材料力学性能及增强机制
采用分子动力学方法(MD)对单层石墨烯纳米片(GNPs)与单面及双面Ni包覆单层GNP (Ni-GNP、Ni-GNP-Ni)增强镁基复合材料(GNP/Mg、Ni-GNP/Mg、Ni-GNP-Ni/Mg)在单轴拉伸作用下的力学性能进行了研究,并与含有空位缺陷的双面Ni包覆单层GNP (Ni-defected GNP-Ni)及双面Ni包覆多层GNPs (Ni-nGNPs-Ni)增强镁基复合材料(Ni-defected GNP-Ni/Mg、Ni-nGNPs-Ni/Mg (n为GPNs层数))拉伸性能进行了对比。研究结果表明:GNPs的加入可以显著增强镁基复合材料的力学性能,与单晶Mg相比,GNP/Mg纳米复合材料在300 K及应变速率为1×109 s-1时的拉伸强度和弹性模量分别提高了32.60%和37.91%,而Ni-GNP-Ni/Mg的拉伸强度和弹性模量分别提高了46.79% 和54.53%;此外,Ni-defected GNP-Ni/Mg复合材料的弹性模量和拉伸强度较GNP/Mg有较大的提高,但其断裂应变提高的幅度较小;而Ni-GNP/Mg复合材料的拉伸强度和断裂应变较GNP/Mg有较大的提高,但其弹性模量提高的幅度较小。Ni-GNP-Ni/Mg基复合材料的弹性模量、拉伸强度和断裂应变随着温度的升高而降低,表现出了温度软化效应,但复合材料弹性模量的变化对温度不敏感。随着Ni-nGNPs-Ni中n的增加,即增强体体积分数增大时,复合材料弹性模量、拉伸强度及断裂应变均随之增大,复合材料表现出良好的综合力学性能。最后通过对原子结构演化的分析,发现Ni-GNP-Ni/Mg纳米复合材料的强化机制主要是界面强化、载荷的有效传递及位错强化。
关键词:
纯Mg及镁合金由于密度低、在地壳中的含量丰富等优点,在汽车、航空航天和电子行业等领域具有很好的应用前景,但Mg的脆性和低强度限制了镁合金的广泛应用[1]。为了改善镁合金的力学性能以满足不同领域对其的使用要求,越来越多的学者开始研究以纳米颗粒和纤维为增强相的镁基纳米复合材料[2,3]。随着石墨烯纳米片(graphene nanoplatelets,GNPs)的发现[4]和对其研究的日渐深入,因其具有独特的结构和优异的力学性能[5,6,7,8]被认为是镁基复合材料的理想增强体之一。近期,Du等[9]使用热压和球磨相结合的方法制备了不同质量分数的GNPs增强镁基纳米复合材料(GNPs/Mg),研究表明:GNPs的质量分数越大,复合材料的硬度越高。扫描电镜(SEM)观察显示,GNPs在晶粒内部和晶界处均匀分布,从而有效地提高了复合材料的力学性能。Yuan等[10]研究了GNPs/AZ91合金的力学性能,当在基体合金中加入0.5%GNPs (质量分数)之后,复合材料的屈服强度和延伸率相比基体提高了76.2%和24.3%。并通过SEM和透射电镜(TEM)等实验手段分析得出,复合材料性能的增强机制主要是晶粒细化、强的界面结合和位错强化等。Xiang等[11]制备了2种含有不同质量分数GNPs的镁基纳米复合材料(0.10%GNPs/Mg和 0.25%GNPs/Mg),通过分解熔融沉积技术使得GNPs在基体中均匀分布,有效地提高了材料的整体性能。
尽管目前已有一些有关GNPs/金属基纳米复合材料力学性能的实验研究报道,但由于实验设备和技术的限制,在原子尺度上研究其力学行为还鲜见报道。分子动力学(molecular dynamics,MD)模拟是在原子尺度研究材料力学行为的有效计算方法,在纳米复合材料纳米尺度力学性能研究方面有着较广泛的应用。Rong等[12]使用MD方法计算了不同几何尺寸和手性的GNPs对铝基复合材料力学性能的影响,结果表明,加入GNPs可以增强基体的弹性模量和强度,且性能提高与GNPs的尺寸有关;复合材料的断裂主要由GNPs控制。Rezaei[13]使用MD模拟研究了GNPs/Cu复合材料单轴拉伸性能,结果表明,GNPs可以显著提高复合材料的强度和断裂应变、刚度及韧性。其原因在于GNPs可以提供有效的屏障,能防止金属层的剪切流动和位错传播,使施加的应变能量在材料内部更均匀地扩散。Barfmal和Montazeri[14]研究了2种不同体积分数 (3%和5%)的GNPs/SiC纳米复合材料的力学性能,结果表明,随着GNPs体积分数的增加,弹性模量提高了31.7%。此外,Zhou等[15,16]使用MD模拟研究了碳纳米管(CNT)和Ni-CNT增强单晶Mg的性能,研究结果显示,表面镀镍CNT可以有效提高界面力学性能,使复合材料整体力学性能增强,且其弹性模量随着嵌入基体的CNT的半径增大而增大,随着系统温度的增加而降低。
虽然人们对GNPs/Mg复合材料的力学性能进行了较多的实验研究,但各种因素对该类复合材料力学性能的影响规律及其强化机理仍然不甚清楚。因此,本工作基于MD模拟方法,研究了不同GNPs增强镁基复合材料的拉伸力学性能和增强机制。通过对拉伸过程和微观结构演化的分析,得出了不同影响因素对GNPs/Mg拉伸性能的影响规律以及复合材料在纳米尺度的变形强化机理。
本工作利用MD模拟软件LAMMPS[17]研究了单层GNP/Mg、单面Ni包覆单层GNP/Mg (Ni-GNP/Mg)、双面Ni包覆单层GNP/Mg (Ni-GNP-Ni/Mg)以及双面Ni包覆多层GNPs/Mg (双面Ni包覆n层GNPs/Mg,Ni-nGNPs-Ni/Mg)的单轴拉伸力学性能,并以Ni-GNP-Ni/Mg为例分析了复合材料力学性能提高的增强机制。Mg基体沿3个方向的晶向分别为[
图1 不同石墨烯纳米片(GNPs)增强镁基复合材料模型
Fig.1 Different models of graphene nanoplatelets (GNPs) reinforced Mg matrix composites
(a) Ni-GNP-Ni/Mg (b) Ni-3GNPs-Ni/Mg (c) Ni-5GNPs-Ni/Mg
首先利用共轭梯度法让模型的能量最小化,然后在300 K及等温等压(NPT)系综下对模型弛豫40 ps,消除模型的内部应力,使其达到稳定的结构。接着在正则(NVT)系综下保持温度不变(300 K),沿z轴施加应变率为1×109 s-1的拉伸载荷直到模型断裂失效。整个计算过程时间步长为1 fs,温度通过Nose-Hoover热浴法进行控制,压强通过Parrinello-Rahman恒压器法控制,计算过程中使用Velocity Verlet算法对运动方程进行积分。采用OVITO[19]可视化分析软件中的分析方法对模拟结果进行后处理。
复合材料的应力(σ)通过Virial应力理论[20]计算:
式中,V是系统的体积;mi、ri、ui分别是原子i的质量、位置和位移;
本工作使用Sun等[21]的嵌入原子方法(embedded atom method,EAM)势函数研究Mg原子之间的相互作用;使用Stuart等[22]的AIREBO (adaptive intermolecular reactive empirical bond order)势函数研究GNPs中C原子之间的相互作用,其中C—C键的截断半径为R1=0.2 nm[23];采用Bond-order势函数[24]计算Ni—Ni、Ni—C之间的相互作用。 Mg—C、Mg—Ni及GNP—GNP之间的相互作用使用Lennard-Jones (L-J)势函数[14,15,16]描述,截断半径为1 nm。
L-J势函数(ELJ(r))的表达形式为:
式中,
Table 1
为了验证计算的准确性,首先使用1.2节的方法和模拟条件计算了不同手性参数的GNP和单晶Mg的拉伸力学性能。计算中所用单层GNP的尺寸为10.70 nm×0.34 nm×12.07 nm,与基体中增强体的尺寸相等,共包含4900个C原子。图2a和b分别为扶手椅(Armchair)型和锯齿(Zigzag)型GNP模型,其中箭头表示加载方向。计算得到的应力-应变曲线如图3所示。
图2 不同手性参数GNP的拉伸示意图
Fig.2 Schematics of simulation model of GNP with different chiral parameters of armchair (a) and zigzag (b) subjected to uniaxial tensile loading (F—load)
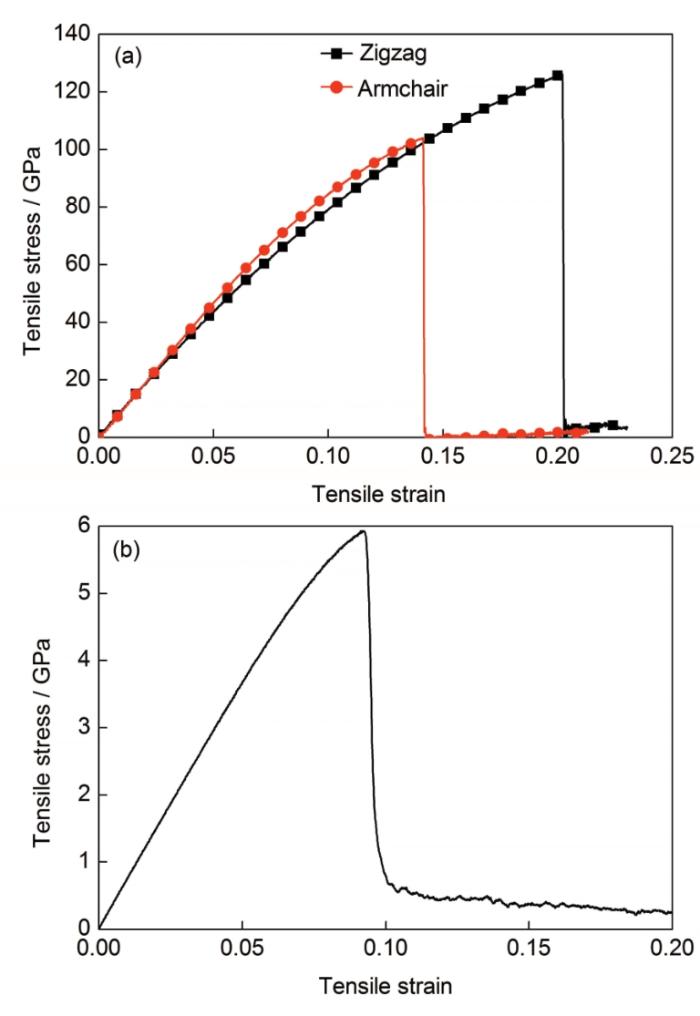
图3 不同手性参数的GNP和单晶Mg的拉伸应力-应变曲线
Fig.3 Tensile stress-strain curves of GNP with different chiral parameters (a) and single crystal Mg (b)
图3a为不同手性参数的GNP在300 K下的单轴拉伸应力-应变曲线。经过计算得到Zigzag型GNP的弹性模量为807.5 GPa,极限应力和断裂应变分别是126 GPa和0.202;而Armchair 型GNP的弹性模量为885.4 GPa,极限应力和断裂应变分别是104 GPa和0.142。所得计算值与He等[25]的计算值均吻合良好。图3b为单晶Mg沿[0001]方向拉伸时的应力-应变曲线。由图可见,单晶Mg的应力随着应变的增加达到最大值后有一个剧烈的降落,说明单晶Mg中出现了断裂。对弹性阶段拟合可以得到单晶Mg的弹性模量为69.7 GPa,其极限拉伸应力和断裂应变分别是5.9 GPa和0.093,与Zhou等[16]的计算值相吻合。
为了分析Zigzag型GNP对镁基复合材料的增强效果,首先对单层GNP与单面及双面Ni包覆GNP (Ni-GNP、Ni-GNP-Ni)增强镁基复合材料在单轴拉伸作用下的力学性能进行了模拟,并与含有0.6% (体积分数)空位缺陷但双面Ni包覆的GNP (Ni-defected GNP-Ni)/Mg复合材料拉伸行为进行了对比。
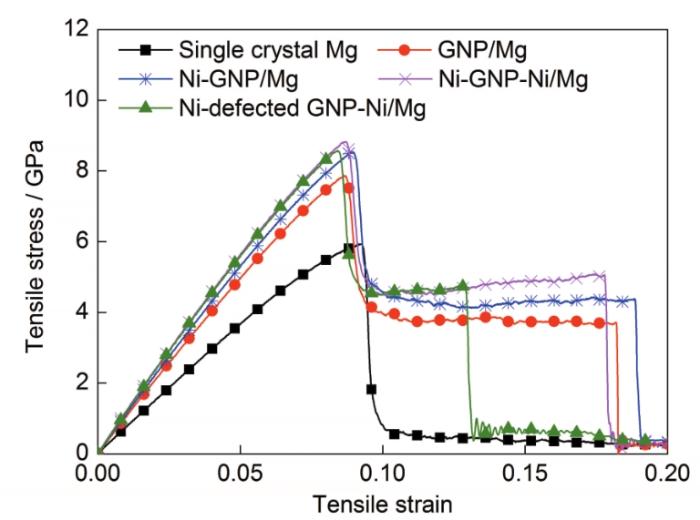
图4为不同GNP增强镁基复合材料的拉伸应力-应变曲线。由图可以看到,加入GNP之后的复合材料的弹性模量及最大拉伸应力均大于单晶Mg,且达到最大拉伸应力之后,复合材料的应力首先减小到一个数值,然后随着应变的增加应力保持一个较稳定的状态或继续增大。GNP/Mg和Ni-GNP/Mg的应力随着应变的增加基本保持不变;当GNP两面都包覆Ni时,复合材料的应力随着应变的增加再次增加,直到GNP发生断裂,复合材料失效。表2列出了不同复合材料与单晶Mg的典型拉伸性能。由表2可见,与单晶Mg相比,GNP/Mg、Ni-GNP/Mg、Ni-GNP-Ni/Mg与Ni-defected GNP-Ni/Mg的弹性模量分别增长了37.91%、46.80%、54.53% 和53.59%。由图4和表2可知,随着GNP表面包覆Ni的体积分数的增加,复合材料的弹性模量增大,且最大拉伸应力也增大,这主要是由于GNP表面的Ni原子使得Mg—C之间的结合强度增大[26],综合力学性能提高;当GNP中存在小体积分数(<1%)的空位缺陷时,对复合材料弹性阶段的影响不大,但会导致复合材料提前断裂。
图4 GNP/Mg复合材料拉伸应力-应变曲线
Fig.4 Tensile stress-strain curves of different GNP/Mg nanocomposites
表2 不同GNP/Mg复合材料与单晶Mg的力学性能
Table 2
Material
Failure strain
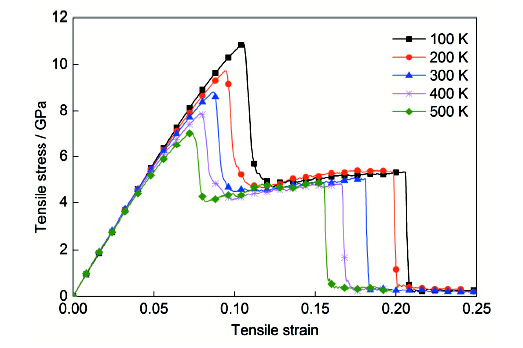
此外,还研究了在相同的应变率下(1×109 s-1) 温度对Ni-GNP-Ni/Mg拉伸力学性能的影响,计算结果如图5所示。由应力-应变曲线可以看到,随着温度的增加,复合材料的弹性模量、峰值应力和对应的应变以及断裂应变降低,而断裂应力有较小的下降,复合材料总体上表现出了温度软化效果。但温度对复合材料塑性流动阶段的力学性能影响并不大,这主要是因为在此阶段复合材料性能的温度敏感性主要依赖于GNP性能的温度敏感性,而温度对GNP性能的影响比较小[27]。
图5 不同温度下Ni-GNP-Ni/Mg的拉伸应力-应变曲线
Fig.5 Tensile stress-strain curves of Ni-GNP-Ni/Mg nanocomposites at different temperatures and a constant strain rate of 1×109 s-1
图6显示了不同层数GNP增强镁基复合材料的应力-应变曲线。可见,随着GNP层数的增加,复合材料的弹性模量、峰值应力及对应的应变、断裂应力和断裂应变都进一步增大。由表3可知,与Ni-GNP-Ni/Mg相比,Ni-3GNPs-Ni/Mg和Ni-5GNPs-Ni/Mg的弹性模量分别增大了49.83%和88.59%。经过非线弹性阶段之后,可以看到应力随着应变增大的趋势也与GNP的层数(即体积分数)有关,体积分数越大,应力增大的斜率也越大。在实际实验中,GNP含量过高时,由于它独特的二维结构和GNP之间的van der Waals作用可能会导致其团聚[7],使得实际的性能要比理论计算值低。
图6 不同层数的GNPs/Mg复合材料的拉伸应力-应变曲线
Fig.6 Tensile stress-strain curves of GNPs/Mg nanocomposites with different layers of GNP
表3 Ni-nGNPs-Ni/Mg复合材料各项力学性能
Table 3
Material
Failure strain
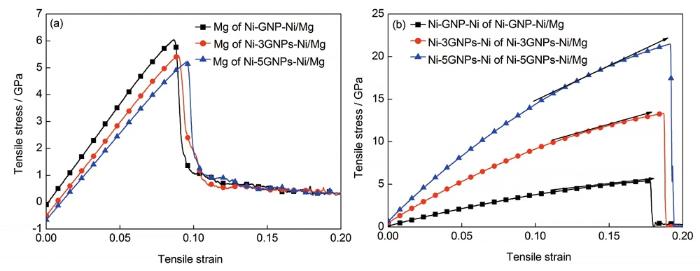
为了更进一步理解复合材料中各组分对其力学性能的贡献,图7以不同层数的Ni-nGNPs-Ni/Mg为例计算了复合材料中基体与增强体的应力-应变曲线。图7a表示的是基体对复合材料力学性能的贡献。可以看到,在弹性及非线弹性阶段,增强体的体积分数越小,对应的基体承受载荷的能力越大。达到峰值应力后,基体的应力迅速降低,说明基体中出现了空隙、位错等缺陷,复合材料进入塑形流动直至破坏阶段。由图7b可以看到,复合材料到达塑性流动阶段之后,增强体的应力变化与基体相反,随着应变的增加继续上升,复合材料在该阶段仍然可以承受载荷的作用。GNP的层数对其应力有重要的影响,在应变相等的情况下,应力随着GNP层数的增加而增大。由图7b可知,GNP在非线性弹性阶段的应力增加的斜率虽然小于线弹性阶段的斜率,但还是层数越多,斜率越大,即应变硬化作用更大,这一规律在复合材料的整体应力-应变曲线中也有所体现。
图7 基体和增强体拉伸应力-应变曲线
Fig.7 Tensile stress-strain curves of Mg matrix (a) and Ni-coated different GNP reinforcements (b) in the GNPs/Mg composites
单晶Mg及Ni-GNP-Ni/Mg复合材料中Mg基体在拉伸过程中的原子结构演化过程分别如图8a~c及图8d~f所示。由图可以看到,从拉伸应变ε=0.094时刻开始,单晶Mg中随机出现了多个空位缺陷;当ε=0.095时,缺陷成核并沿着不同取向的晶面扩展;当ε=0.1时,其内部有较大面积的贯穿型原子结构的错排,并含有孔洞及少量相变原子,单晶Mg失效。对于复合材料中的Mg基体,在拉伸应变ε=0.087时基本上是完美的;在拉伸应变ε=0.088时,可以看到Mg基体和GNP的界面处开始出现多处错排原子结构,但面积较小;当ε=0.1时,可以明显看到缺陷从不同界面处沿着Mg基体内部的晶面生长,复合材料的变形及强度主要受界面控制。
图8 单晶Mg和Ni-GNP-Ni/Mg复合材料中Mg基体在拉伸变形过程中的原子演化构形图
Fig.8 Molecular dynamics (MD) snapshots of lattice configuration variation of single crystal Mg without (a~c) and with Ni-GNP-Ni (d~f) in the Ni-GNP-Ni/Mg composite during tensile process (ε—tensile strain)
(a) ε=0.094 (b) ε=0.095 (c) ε=0.1 (d) ε=0.087 (e) ε=0.088 (f) ε=0.1
图9a~c和d~f分别为复合材料中GNP与Ni-GNP-Ni在拉伸过程中的构象演化图。尽管GNP与Ni-GNP-Ni在初始弹性变形时刻均具有比较完整的原子结构构象(图9a和d),其弹性变形能通过C—C键的伸长被保存,但在随后的拉伸变形过程中二者的原子构象出现了较大的差别。在ε=0.0189时,GNP层尽管没有开始断裂,但其内部局部已经出现较大的缺陷(图9b),这是因为GNP与Mg基体的延伸率不同而有相对运动趋势,从而使得局部发生应力集中所致;在ε=0.19 (即达到GNP层断裂应变)时,复合材料中的GNP出现断裂,同时由于受到两侧Mg基体较弱的约束发生褶皱现象(图9c)。而对于Ni-GNP-Ni,即当GNP层双面都包覆Ni原子时,可以看到其断裂先在边缘处出现(图9e),这是由于双面包Ni的GNP与Mg基体的界面之间有较强的键合作用,靠近中心界面处两相变形协调性增强,但在拉伸过程中边缘处产生附加应力所致;随着拉伸过程的进行,在ε=0.188时边缘处出现的裂纹沿着一定的角度较快地扩展到GNP内部发生最终破坏,但Ni包覆GNP受到两侧Mg基体较强的约束没有发生翘曲(图9f)。
图9 复合材料中未包Ni和包覆Ni的GNP的拉伸变形演化过程
Fig.9 MD snapshots of lattice configuration variation of uncoated-Ni GNP (GNP) (a~c) and double side Ni-coated GNP (Ni-GNP-Ni) (d~f) in the GNP/Mg composite during tensile process
(a) ε=0.188 (b) ε=0.189 (c) ε=0.19 (d) ε=0.186 (e) ε=0.187 (f) ε=0.188
为了进一步探讨Ni-GNP-Ni/Mg复合材料的强化机理,图10a~d和e~h分别给出了GNP/Mg与Ni-GNP-Ni/Mg复合材料中界面附近位错的演化和分布。由图可以看到,在ε=0.087时,2种复合材料界面处开始有位错产生(图10a和e)。随着塑性应变从ε=0.087增大到ε=0.2,2种复合材料界面附近均出现了不同结构和分布的位错演化,但在整个位错演化的过程中,Ni-GNP-Ni/Mg复合材料界面附近具有较多的不同类型位错,阻碍了Mg晶体的进一步滑移,Ni-GNP-Ni/Mg复合材料强度得以提高。此外,在ε=0.2时,2种复合材料虽然都发生了脆性破坏(图4),但此时GNP/Mg复合材料中的GNP整体已发生较大的损伤破坏,而Ni-GNP-Ni/Mg复合材料中的Ni-GNP-Ni及其与基体界面附近的整体损伤较小,损伤起始于基体并最终由Ni-GNP-Ni局部破坏导致该类复合材料失效,因此较GNP/Mg复合材料具有较高的抗拉伸破坏性能。
图10 GNP/Mg与Ni-GNP-Ni/Mg复合材料中位错的演化和分布
Fig.10 Dislocation evolutions and distributions of GNP/Mg (a~d) and Ni-GNP-Ni/Mg (e~h) composites
(a, e) ε=0.087 (b, f) ε=0.1 (c, g) ε=0.13 (d, h) ε=0.2
综上所述,尽管在拉伸时复合材料中GNP与Ni-GNP-Ni最终都呈现脆性断裂,但由于Ni包覆GNP与Mg基体的界面之间有较强的键合作用,在复合材料拉伸过程中,Ni包覆GNP受到两侧Mg基体的约束而没有发生翘曲;对于Mg基体,与Ni包覆GNP接触的界面附近基体处首先发生损伤成核,继而沿着Mg基体中某个晶面生长到最终破坏。另一方面,在拉伸载荷的作用下,在Mg基体和Ni-GNP-Ni增强体的界面附近会形成较多的位错,随后的位错运动会由于位错堆积产生的应力场受到阻碍,从而使得复合材料的力学性能增强。Ni包覆GNP/Mg复合材料的强化机制主要包括界面强化、载荷传递及位错强化,Ni包覆GNP与Mg基体之间的较强的界面结合,使得载荷能从基体有效地传递到增强体上;同时,Ni包覆GNP周围产生了较高密度的位错,阻碍了Mg晶体的滑移,从而提高了复合材料的强度。
(1) 与基体Mg相比,单层GNP/Mg、双面包覆Ni的含少量缺陷单层GNP的Ni-defected GNP-Ni/Mg以及Ni包覆单层GNP的Ni-GNP-Ni/Mg复合材料的弹性模量、最大拉伸应力和断裂应变均显著增大。按改进综合力学性能的排序为:双面包Ni的Ni-GNP-Ni/Mg>单面包Ni的Ni-GNP/Mg>表面没有包Ni的GNP/Mg>双面包覆Ni的含有少量缺陷GNP的Ni-defected GNP-Ni/Mg复合材料。其中,对于双面包Ni的Ni-GNP-Ni/Mg复合材料,复合材料的拉伸性能随GNP体积分数的增大而增大;当GNP中含有小体积分数的空位缺陷时(<1%),复合材料的断裂失效应变增加的幅度最小。
(2) 单晶Mg的拉伸损伤随机出现在其内部,并迅速成长从而形成滑移面,而含有表面包Ni的GNP的Mg基体损伤会在界面多处成核并扩展最终失效。此外,表面包Ni的GNP与Mg基体之间有较强的键合作用,这种作用一方面使得载荷可通过界面由基体传递到GNP增强体,另一方面使得GNP受到界面两侧基体较强的约束出现较少的内部缺陷。同时,拉伸过程中Ni-GNP-Ni/Mg复合材料界面处产生了较高密度的位错,阻碍了Mg晶体的滑移,也使得复合材料性能得以强化。上述界面强化、载荷有效传递及位错强化是Ni包覆GNP/Mg复合材料的主要增强机制。
1 计算方法
1.1 计算模型
图1

1.2 模拟步骤
1.3 势函数
Interatomic interaction
R / nm
Mg—C
0.0028
0.35015
Mg—Ni
0.0024
0.2965
GNP—GNP
0.00284
0.34
2 结果和讨论
2.1 GNP和单晶Mg的力学性能
图2
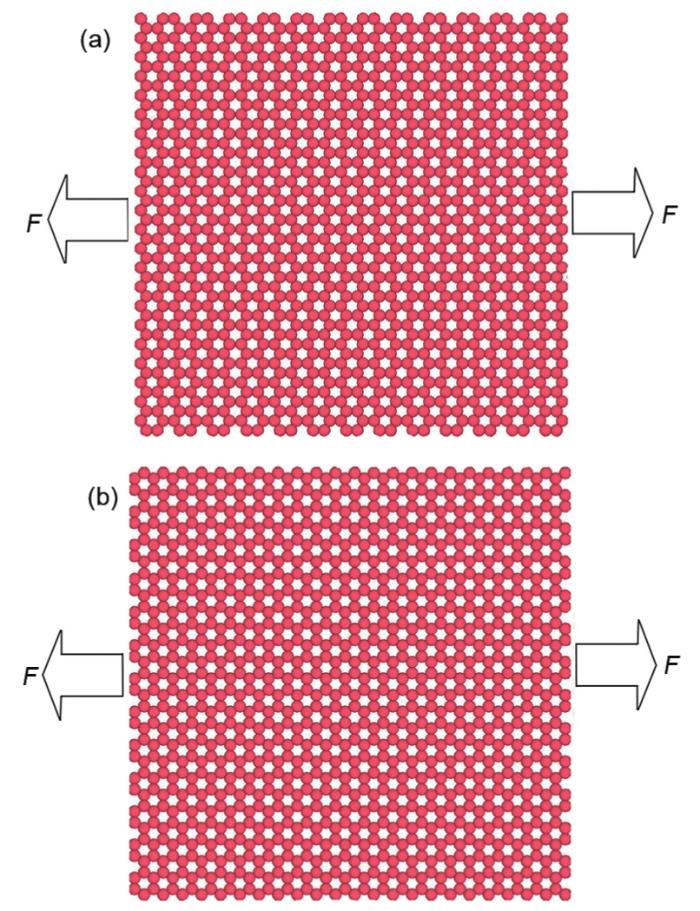
图3
2.2 单层GNP/Mg的力学性能
图4
Volume fraction / %
Elastic modulus GPa
Peak stress GPa
Fracture stress GPa
GNP
Mg
Single crystal Mg
0.0
100.0
69.70
5.92
5.92
0.094
GNP/Mg
3.2
96.8
96.12
7.85
3.61
0.182
Ni-GNP/Mg
4.0
96.0
102.32
8.40
4.36
0.188
Ni-GNP-Ni/Mg
5.2
94.8
107.71
8.69
5.24
0.176
Ni-defected GNP-Ni/Mg
5.2
94.8
107.05
8.37
4.72
0.126
图5
2.3 GNPs体积分数的影响
图6

Volume fraction / %
Elastic modulus GPa
Peak stress GPa
Fracture stress GPa
GNP
Mg
Ni-GNP-Ni/Mg
5.2
94.8
107.71
8.69
5.24
0.176
Ni-3GNPs-Ni/Mg
11.8
88.2
161.38
13.31
11.86
0.187
Ni-5GNPs-Ni/Mg
18.0
82.0
211.28
17.89
18.95
0.192
图7
2.4 Ni-GNP-Ni/Mg复合材料的增强机制
图8

图9

图10

3 结论
来源--金属学报







 沪公网安备31011202020290号
沪公网安备31011202020290号
