分享:脉冲磁场对TC4钛合金微观结构的影响及其机理探究
研究了脉冲磁场对TC4钛合金微观结构的影响规律,发现经磁感应强度为2 T、脉冲频率为5 Hz、脉冲次数为 100次的脉冲磁场处理后,TC4钛合金的位错密度及晶界角度会发生显著变化。XRD测试结果显示,经脉冲磁场处理后TC4钛合金的位错密度提高约10.9%。采用EBSD测试得到TC4钛合金微区的KAM分布,发现经脉冲磁场作用后,TC4钛合金的位错密度发生显著变化,具体表现为:晶内位错分布更加均匀,局部高位错密度区消失;晶界附近的位错分布发生变化,同时晶界角度发生改变,小角度晶界减少而重位点阵(CSL)晶界(Σ11)增多。讨论了脉冲磁场对TC4钛合金微观组织影响的可能原因:脉冲磁场引起位错钉扎处的电子能态发生转变,使钉扎处空位或杂质原子易于移动。位错在材料内应力场提供的弹性能作用下更易脱钉扎,从而使得位错分布发生变化,材料微观组织发生改变。
关键词:
已有研究中,认为脉冲磁场引起的材料内部位错运动是其残余应力改变的一个重要原因,文献[10,12,13]研究了脉冲磁场对低碳钢残余应力的影响,认为脉冲磁场引起磁致振动使得位错运动,从而降低残余应力。文献[8]测量了脉冲磁场下低碳钢试样表面的应变,认为磁致振动的应力幅度停留在弹性区,不足以引起位错运动,解释其运动应采用其它机理。文献[9,11,14]认为,磁致塑性效应是铁基材料在脉冲磁场作用下位错运动的主要原因。磁致塑性是在磁场作用下,晶体材料中包含缺陷的亚稳态结构发生复杂多级过程的现象[15],多级过程具体表征为电子自旋能态改变、点缺陷移动及位错重新分布。非金属材料(如NaCl、LiF、CsI等)的磁致塑性研究有若干报道[16,17,18]。文献[19,20,21,22,23,24]报道了脉冲磁场引起非铁磁性金属材料(如Al、Mg-7Zn等)位错的运动,也以磁致塑性效应作为解释。本工作对脉冲磁场处理前后的TC4钛合金试样的同一微区进行观察,发现经脉冲磁场处理后,TC4钛合金的位错密度及晶界角度有了显著的变化,讨论了脉冲磁场对TC4钛合金微观组织影响的可能原因。本工作对晶体磁致塑性的机理研究提供了有益补充,同时为改善如TC4钛合金的非铁磁性金属材料的残余应力提供了可能的新方法。
实验材料选取TC4钛合金叶轮坯料,原始尺寸为直径200 mm×30 mm,利用快走丝线切割取坯料底面中心附近材料,将其加工成5 mm×5 mm×6 mm的试样若干,其中5 mm×5 mm面为测试面,磨抛至镜面。使用本课题组自制的磁化器[9]对磨抛后的TC4钛合金试样进行脉冲磁场处理,处理参数为:磁感应强度 B=2 T,脉冲频率f=5 Hz,脉冲次数为100次。使用
使用APD-2000 X射线衍射仪(XRD)对脉冲磁场处理前后TC4钛合金试样的位错密度进行测试,扫描范围为3°~100°,扫描速率为2°/min,电压为10 kV。使用PHI710俄歇谱仪的电子背散射衍射(EBSD)附件对TC4钛合金试样脉冲磁场处理前后进行原位观察:(1) 将未经脉冲磁场处理的试样放入俄歇谱仪的真空腔,在扫描电镜(SEM)下选定试样一个扫描微区,扫描区域为30 μm×30 μm,设定扫描步长为每点0.07 μm并进行EBSD扫描,记录数据;(2) 对该试样进行脉冲磁场处理;(3) 将脉冲磁场处理后的试样再次放入俄歇谱仪的真空腔,在SEM下找到试样脉冲磁场处理前的EBSD扫描微区,以同样的扫描步长进行EBSD扫描并记录数据;(4) 对比脉冲磁场处理前后试样同一微区的EBSD结果并分析。试样进行EBSD测量前需要进行电解抛光去应力层,以6%HClO4+94%CH3COOH (体积分数)作为电解液,在常温下对试样进行电解抛光,电解抛光电流设置为0.2~0.3 A,时间为60 s。
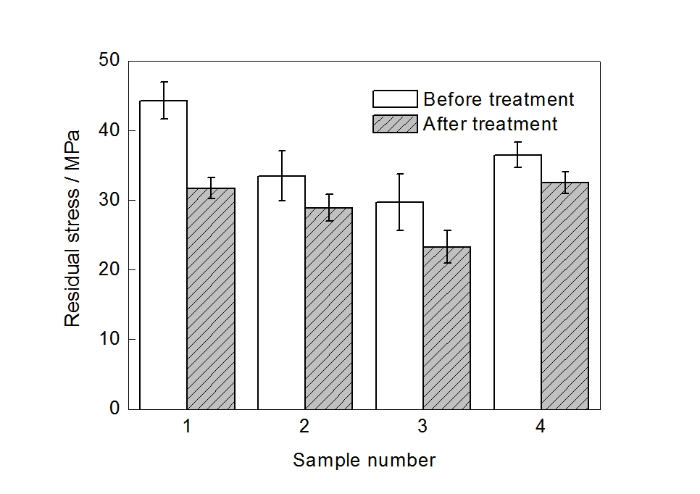
图1 TC4钛合金试样脉冲磁场处理前后平均残余应力
Fig.1 Average residual stresses of the samples before and after pulsed magnetic treatment
图2 TC4脉冲磁处理前后XRD谱
Fig.2 XRD spectra of TC4 samples before and after pulsed magnetic treatment
式中,K=2sinθ/λ,ΔK=2cosθ?Δθ/λ (θ为衍射角,Δθ为2θ处峰的半峰宽,λ为衍射波波长),b为Burgers矢量模,M为与位错密度有关常数,
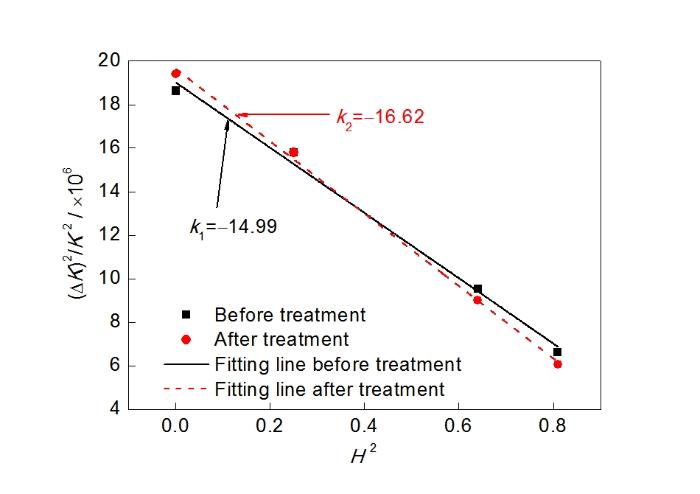
图3 (ΔK)2/K 2~H 2线性拟合图
Fig.3 (ΔK)2/K 2~H 2 linear fitting graph (K is expressed as 2sinθ/λ, ΔK is expressed as 2cosθ?Δθ/λ, θ is the angle of the peak in XRD spectrum, λ is the XRD wave length, H 2 is expressed as equation (2), k1 is the slope of linear fitting line before treatment, k2 is the slope of linear fitting line after treatment)
图4 脉冲磁场处理前后TC4试样微区KAM分布云图
Fig.4 Low (a, b) and locally high (c, d) magnified KAM distributions of the TC4 sample before (a, c) and after (b, d) pulsed magnetic treatment (The KAM distribution after treatment is more homogeneous than that before treatment totally. Positions 1, 2 and 3 in Figs.4a and b as an example indicate the variation of KAM near the grain boundaries. The boxes in Figs.4c and d forcefully indicate the reduction of KAM in the specific grain while the ellipses in Figs.4c and d indicate the increase of KAM in the specific grains. Positions 4, 5 and 6 in Figs.4c and d as an example indicate the variation of KAM and especially the variation of the shape of the grain boundaries)
KAM分布的改变代表了位错分布的改变,总体位错密度呈现均匀化的趋势,晶界附近位错密度的变化显著,推测晶界区域可能存在位错的塞积、穿越及湮没现象,这一推测可从晶界角度变化规律上进一步加以印证。
位错移动过程中遇到障碍物(杂质、晶界等),会出现塞积现象,而晶界壁垒阻碍了位错的移动,形成了局部区域的应力应变集中,当应力应变集中达到一定程度,位错会突破障碍物的能量势垒而穿越晶界[11,31]。位错在晶界处的塞积、穿越及湮没行为,很可能改变晶界角度。图4显示TC4钛合金晶界附近的KAM变化显著,通过OIM软件提取试样观察区域脉冲磁场处理前后的晶界角度并绘制曲线,如图5所示。由图5可知,脉冲磁场作用后TC4试样的晶界角度变化明显,特别是小角度晶界(晶界角度小于10°的晶界)显著下降,而在34°~38°晶界角度区间内的晶界显著增加。钛合金的α相为六方结构,在约36.5°的晶界角度位置存在重位点阵(CSL)晶界,重位点阵周期为11,表示为Σ11。经过脉冲磁场处理后的TC4试样小角度晶界显著减少而Σ11的CSL晶界显著增加。
图5 脉冲磁场处理前后TC4试样晶界角度统计
Fig.5 Grain boundary angle distributions of TC4 samples before/after treatment (Significant reduction of the low-angle grain boundaries can be found, while there are also significant increase of the grain boundaries with the angle within the scope of 34°~38°, which may well be the Σ11 boundaries (36.5°, a kind of CSL boundaries of α-phase of TC4 alloy)
小角度晶界的形成和演变很大程度上依赖于位错运动[32]。以对称的简单倾斜小角度晶界为例,它由纵向等距排列的刃型位错产生。其晶界角度可表示为材料的Burgers矢量模与纵向刃型位错的间距的比值。通过实验观察到的小角度晶界的比例降低,以及晶界附近位错密度分布变化现象,可推测小角度晶界区的位错可能发生运动而进入或脱离晶界区域,同号位错塞积加大晶界角度,异号位错相遇湮没从而降低晶界角度,最终使得小角度晶界角度发生变化。
另一方面,钛合金α相中的CSL晶界Σ11(36.5°)邻域的晶界含量升高。理论上,按照严格几何特征配合形成的CSL晶界,其晶界处的原子并非处于平衡状态,因此原子弛豫会使得晶格发生畸变[32]。Balluffi等[33]讨论了原子弛豫后的CSL晶界可认为是原有的严格几何模型中引入了位错,使得其晶界角度发生偏转。Bishop和Chalmers[34]认为,由于内禀晶界位错的存在使得特殊位置的CSL晶界角度得以在一定区间范围内发生偏移。因此,脉冲磁场驱动的位错引起了特定CSL晶界的含量增多是合理的推测。更进一步,CSL晶界的含量上升,证明晶界能降低,即脉冲磁场处理可以使TC4钛合金晶界能降低,有利于材料更稳定。
基于Frank-Read源位错增殖理论[35],位错受位错线张力(τT)的作用,如下式所示:
式中,G为切变模量,L为位错线长度。接近晶粒尺寸的位错,取L≈10-6 m,b≈10-10 m,G=44.8 GPa,代入计算得τT≈10 MPa。
从位错所受线张力的数量级来看,材料内部的残余应力可提供驱动力。然而位错在杂质原子、空位以及晶界处形成钉扎点,钉扎点将位错割裂成若干部分,根据式(3)可知,位错张力会成倍增加,使得位错无法运动。因此,若脉冲磁场作用能提高位错脱钉的效率,很大程度上能促使位错在原有应力场作用下发生移动,产生磁致塑性效应。目前,针对非铁磁性金属材料在磁场作用下磁致塑性的理论研究并不充分,磁致塑性的理论研究集中在非金属材料中。本工作主要借鉴前人关于非金属晶体磁致塑性的相关机理,对TC4钛合金在磁场中的磁致塑性效应的可能原因进行推测。
图6 电子对自旋能态及相互转化关系
Fig.6 Transforming relationship of the spin energy state of the electron pair (The solid arrows indicate the transformation between these two states happens frequently while the hollow arrows indicate the transformation happens rarely)
式中,ωp为进动角频率,B为磁感应强度,μ为电子磁矩,h为Planck常数。
如图7所示,当处于S态的电子对受到脉冲磁场的作用时,由于Lande因子的微小差异(约10-3~10-4),使得电子对的进动频率产生差异,从而使得位于S态的电子对进入T态的频率从几乎为0达到了108~109 s-1。由于脉冲磁场作用,使得Es-S更易转换到Es-T从而电子对能够长时间保持在激发态。
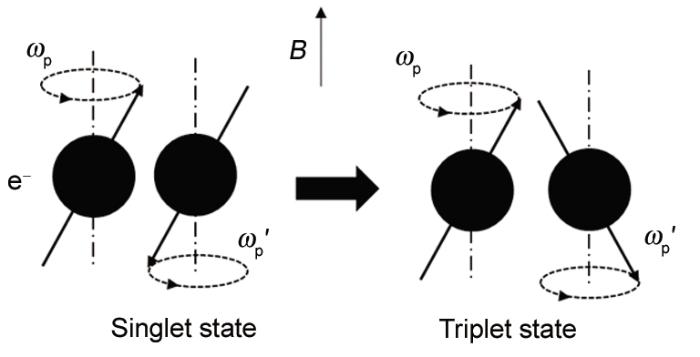
图7 脉冲磁场作用下电子对自旋状态转换示意图
Fig.7 Transformation of the state of electron spin under pulsed magnetic field (Due to the pulsed magnetic field (B), the Larmor precession angular frequency of the electron pair changes faintly (ωp→ωp?), which produces a chance for the electron pair to transform their state from singlet to triplet)
针对TC4钛合金,在磁场作用下出现位错脱钉的现象,位错钉扎处的缺陷处电子可能同样经历了能态的转变。由于金属键与共价键都是源自电子与原子之间的相互作用,基于非金属晶体的磁致塑性理论,可推测脉冲磁场可能引起TC4钛合金位错钉扎处缺陷的电子能态转变,使得位错更易脱钉而在原有力场作用下发生移动。位错的运动使得晶界角度发生一定的改变,包括小角度晶界的减少以及CSL晶界的增多,使系统能量更低;另一方面位错的运动松弛了原有的应力,使材料的残余应力降低。
本工作基于实验及前人研究成果对脉冲磁场作用引起TC4钛合金位错运动的机理提出了合理推测,关于非铁磁性金属材料缺陷处的电子状态转变的根本原因还有待于进一步研究。
(1) 通过XRD与EBSD手段观察到脉冲磁场作用下TC4钛合金的位错分布发生显著变化。一方面,晶内位错发生显著的均匀化,整体位错密度上升;另一方面,晶界处位错发生塞积、穿越及湮没现象,具体表现在晶界KAM分布的增大、减小及晶界角度的改变。这可能是由于位错运动引起的小角度晶界含量降低和CSL晶界Σ11的含量升高,使得系统能量降低,更稳定。
(2) 应用磁致塑性理论对脉冲磁场作用下位错运动机理做了探讨。针对TC4钛合金,脉冲磁场作用促进了位错钉扎点的电子能态转变,使得位错钉扎点能量升高,钉扎阻力减小,位错在原有应力场作用下,更易产生脱钉扎,从而发生运动。位错的运动引起了晶界角度的变化和残余应力的降低,体系趋于稳定。
1 实验方法
2 实验结果
2.1 残余应力
图1
2.2 基于XRD的脉冲磁场处理前后TC4钛合金位错密度统计
图2

图3
2.3 基于EBSD的脉冲磁场处理前后TC4钛合金位错分布及晶界角度结果
2.3.1 基于KAM的位错分布
图4

2.3.2 晶界角度变化
图5

3 分析讨论
图6
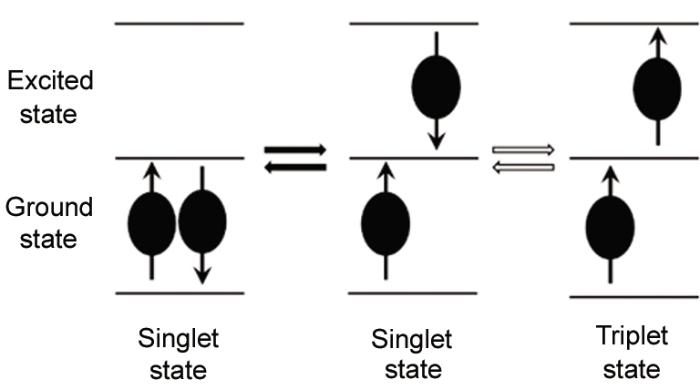
图7
4 结论
来源--金属学报







 沪公网安备31011202020290号
沪公网安备31011202020290号
