分享：X80钢焊接残余应力耦合接头组织不均匀下氢扩散的数值模拟

张体明1, 2, 赵卫民1, , 蒋伟1, 王永霖1, 杨敏1

1 中国石油大学(华东)材料科学与工程学院 青岛 266580
2 南昌航空大学航空制造工程学院 南昌 330063

摘要

关键词： X80管线钢 ; 煤制气 ; 焊接接头 ; 残余应力 ; 氢富集

预计至2030年,全球能源的需求量将增长45%,而到本世纪末将增长3倍[1]。与此同时,由传统能源带来的环境污染和温室气体排放等问题也日益凸显。作为新型清洁高效能源的代表,氢将会在未来的社会发展中起到至关重要的作用[2]。例如,发展含氢煤制天然气行业被认为是传统能源清洁利用的典范,国家能源局印发的《煤炭深加工产业示范“十三五”规划》中明确提出了2020年实现煤制天然气产能达到170×108 m3/a的目标。为了将内陆生产的煤制气输送到沿海地区,势必涉及高压含氢气体的输送问题,而管道无疑是运输方式的首选[3]。但是高压环境下H会扩散进入材料内部,进而降低输送管线的塑性和断裂韧性[4]。为减少建设成本,英国曾做过采用现有天然气管线进行天然气和H2混合输送的可行性调查[5],但调研过程中并未对管线特别是管线焊接接头部位的氢脆失效风险展开针对性的系统研究。焊接是长输管线的重要连接工艺,其热作用会导致接头部位出现严重的组织不均匀[6,7,8]和复杂的残余应力[9,10,11],性能与母材相比发生严重恶化,极有可能加剧氢致脆化失效的风险。氢扩散是材料发生氢脆失效的前提条件[12,13],因此研究和揭示氢在焊接接头中的扩散和富集行为,是进一步明确焊接接头薄弱区域,评判煤制气管线等临氢管线氢脆失效风险的基础和关键。

焊接热过程所导致的接头组织不均匀势必影响接头各亚区的氢扩散参数,如何确定各区的氢扩散参数对接头部位氢富集的评判至关重要。氢渗透实验方法是获得氢在材料中的扩散系数、溶解度、氢浓度等参数的重要手段。但是对于热影响区而言,由于其跨度很小,并且随着距离焊缝位置的不同,所经历的峰值温度也不相同,存在严重的组织差异,所以直接从接头处切取热影响区试样进行氢渗透实验的方法难以保证测试精度。鉴于此,本文作者前期工作[14,15]采用焊接热模拟的方法,使试样经历与实际焊接过程相同的热循环过程,以获得放大的试样,并通过高压气相氢渗透实验获得了各区的氢扩散系数、吸附氢浓度、氢溶解度等关键参数。除此之外,焊接残余应力也是影响氢扩散的另一重要因素[16],与接头组织不均匀产生叠加效应,极易诱发焊接接头局部氢富集,进一步增加了管线氢致脆化的可能性和复杂程度。但是通过氢渗透实验仅能研究单一因素作用下材料中的氢渗透行为,不能确定焊接接头多组织共存且耦合残余应力条件下的氢扩散和富集行为,而这恰是影响焊接接头氢致失效的关键。相比而言,数值模拟的方法则弥补了这一不足。蒋文春等[17]采用数值模拟的方法研究发现,存在焊接残余应力梯度的情况下,氢会向接头高应力区富集。遗憾的是,计算过程中将焊接接头作为均质材料处理,并没有考虑焊接接头各区组织差异对氢扩散行为的影响。

本工作选用X80钢螺旋缝埋弧焊管为研究对象,采用ABAQUS软件建立数值模拟计算模型,模拟计算管线焊接残余应力场,并作为氢扩散计算的预定应力场,焊接接头各区的氢扩散参数通过高压氢渗透实验获得,在此基础上模拟计算组织不均匀和残余应力耦合作用下焊接接头中的氢扩散和富集行为,确定焊接接头所能达到的最高氢浓度,为临氢焊接管线的安全评定奠定基础。

1 焊接接头各区氢扩散参数的测定

1.1 实验材料及方法

选用X80钢螺旋缝埋弧焊管,主要化学成分(质量分数,%)为：C 0.06,Si 0.27,Mn 1.81,S 0.002,P 0.011,Ni 0.30,Mo 0.31,Cu 0.28,Nb 0.07,Cr 0.02,Ti 0.015,Fe余量。管线外径为1219 mm,壁厚18.4 mm,焊缝螺距为1760 mm,采取先内焊、后外焊的方式,内焊领先外焊1.5个螺距,焊丝及焊接工艺如表1所示,焊接过程中采用SJ101G型烧结焊剂保护。截取焊接接头部位的试样,打磨、抛光、侵蚀后,利用Leica S6D体式显微镜观察试样宏观形貌,如图1所示。并对接头的尺寸进行测量。

图1   焊接接头形貌及尺寸

Fig.1   Morphology and dimension of welded joint (unit: mm)

采用高压气相氢渗透实验获取焊接接头各区的氢扩散参数,为数值模拟提供基本条件。所用试样尺寸为直径24.0 mm,厚度2.0 mm。其中母材和焊缝区的试样可直接从管线上切取。相比而言,热影响区的范围很小,直接取样难以满足试样的尺寸要求。因此采用Gleeble 3500热模拟试验机制备热影响区的放大试样,按照峰值温度的差异分为粗晶区(CGHAZ)、细晶区(FGHAZ)和部分相变区(ICHAZ)[14]。

氢渗透实验环境为总压12 MPa的模拟煤制气,具体成分(分压)为：H2 0.24 MPa,CO2 0.20 MPa,其余为N2。测试设备采用自行研制的高压气相氢渗透测试系统,温度控制在(40±0.5) ℃。详细的实验过程见文献[14,15]。

1.2 焊接接头各区氢扩散参数

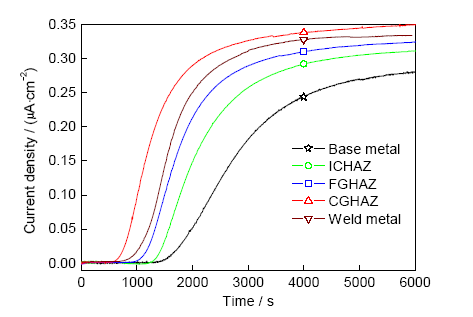
图2所示为X80钢焊接接头各区在模拟煤制气中的氢渗透曲线。可以看出,即使在低氢分压的煤制气环境中也会导致氢渗透的发生。将接头各区的稳态氢渗透电流密度列于表2,并选取暂态氢渗透过程采用Fourier法计算接头各区的氢扩散系数,然后在此基础上依次计算得到吸附氢浓度和氢溶解度[14,15],也列于表2中,以此作为氢扩散数值模拟的已知条件。

图2   焊接接头各区在模拟煤制气中的氢渗透曲线

Fig.2   Hydrogen permeation curves of different sub-regions of welded joint (ICHAZ—intercritical heat affected zone, FGHAZ—fine grained heat affected zone, CGHAZ—coarse grained heat affected zone)

2 氢扩散数值模拟过程及分析

2.1 几何模型构建

根据X80螺旋焊管的外形尺寸及图1所示焊接接头尺寸,取一个螺距建立模型并进行网格划分。为提高焊接接头残余应力及氢浓度的计算精度,将焊缝、热影响区和附近母材区的网格进行细化,同时为了保证计算效率,将远离焊接接头部位的网格划分得相对比较粗大,模型的整体效果和焊接接头局部形貌如图3所示。

图3   管线3D模型及网格划分

Fig.3   3D model of pipeline with mesh division
(a) overall morphology (b) magnification of welded joint

2.2 高温性能参数

在焊接高温作用下,管线钢的热物理参数和力学性能参数会发生较大程度的变化,所以不宜采用室温下的性能参数来进行焊接高温过程所致接头残余应力的计算。本工作采用Yan等[16]给出的X80钢在不同温度下的热物理性能参数。此外,采用Gleeble 3500热模拟试验机进行了X80钢在不同温度下的力学性能分析,实验温度范围为力学性能参数变化较为剧烈的400~1000 ℃,相应的屈服强度和弹性模量如表3所示。其余温度下的性能参数采用插值法计算确定。

2.3 焊接温度场校核

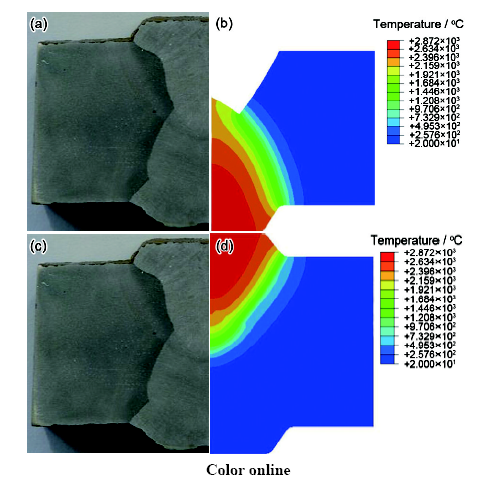
对焊接温度场进行校核是精确计算接头残余应力场,进而分析组织不均匀和残余应力耦合作用下氢扩散和富集行为的重要基础。将数值模拟获得的接头温度场分布云图与实际焊接接头进行比较,并反复对数值模拟参数进行修正,进而获得与实际接头尺寸匹配良好的计算模型。其中,需要着重比较的区域包括焊缝金属和热影响区。以峰值温度不低于1500 ℃的区域代表焊缝金属,750~1500 ℃的区域代表焊接热影响区。图4为实际焊接接头与模拟接头的截面形貌的对比。可以看出,校正后的热源能够准确地模拟实际焊接所用热源。

图4   实际接头与模拟接头的截面形貌

Fig.4   Cross-sectional macrographs of real (a, c) and simulated (b, d) welded joints
(a, b) inner weld (c, d) outer weld

2.4 焊接残余应力

基于温度场校核的结果,进一步计算得到X80钢螺旋焊管焊接接头的残余应力场。其中,Mises应力分布云图如图5a所示。可以看出,螺旋焊管焊缝及热影响区的残余应力显著高于周边的母材区域,Mises等效应力峰值已经逼近600 MPa,即将达到材料的屈服强度。需要说明的是,影响氢扩散的应力为静水应力[18],其值为三向主应力,即管线环向应力、轴向应力以及径向应力的平均值。图5b为从ABAQUS软件中导出所得焊接接头区域的压力分布云图,其定义值为静水应力的负值,因此,图5b间接反映了焊接接头中静水应力的分布特征。观察发现,在板厚中间处的焊缝和热影响区部位存在明显的应力集中。沿图5b中的路径A依次读取各个节点的环向应力、径向应力和轴向应力,并据此计算得到静水应力,绘于图5c中。可以看出,环向应力显著高于径向应力和轴向应力,对静水应力值起主要贡献。此外,焊缝区的残余应力明显高于附近的热影响区及母材区,并且在焊缝向热影响区过渡的区域存在残余应力的突变,即较高的残余应力梯度。根据应力诱导氢扩散理论[19]可知,残余应力梯度会对氢浓度的分布产生影响。

图5   管线焊接残余应力场分布

Fig.5   Stress distributions in welded pipeline
(a) overall morphology
(b) magnification of welded joint with mesh division
(c) residual stress distribution curves along line A in Fig.5b

2.5 氢浓度分布

采用ABAQUS进行氢扩散有限元模拟时主要依据控制方程和本构方程[20]。假定氢在体积为V,表面积为A的物体中扩散,扩散过程满足质量守恒定律,具体表达式为[20]：

${\int }_{?}\frac{\mathrm{d}?}{\mathrm{d}?}\mathrm{d}?+{\int }_{?}???\mathrm{d}?=0$(1)

式中,C表示氢浓度,t表示扩散时间,n表示表面积A的外法线,J表示氢扩散通量。应用散度定理[21],并引入活度变量 $\mathit{\delta ?}$[20],可以推导得到控制方程的表达式为[20]：

${\int }_{?}\left[\mathit{\delta ?}\left(\frac{\mathrm{d}?}{\mathrm{d}?}\right)-\frac{\partial \mathit{\delta ?}}{\partial ?}??\right]\mathrm{d}?+{\int }_{?}\mathit{\delta ?}??\mathrm{d}?=0$(2)

式中,X表示氢扩散的方向。

需要说明的是,氢扩散的驱动力为化学势梯度 $\frac{\partial ?}{\partial ?}$[22],其与J的关系为[22]：

$?=-\frac{\mathit{DC}}{?\left(?-{?}_{\mathrm{Z}}\right)}?\frac{\partial ?}{\partial ?}$(3)

式中,D表示氢扩散系数;R表示气体常数;T表示热力学温度;TZ表示绝对零度;μ表示化学势,其表达式为[22]：

$?={?}_0+?\left(?-{?}_{\mathrm{Z}}\right)\ln ?+{?}_{\mathrm{h}}{?}_{\mathrm{H}}$(4)

式中,μ0为常数; $?$表示氢的活度,当氢分压较低时与氢压相当[23],满足C=?S,其中,S表示氢溶解度;σh为静水应力;VH为氢的偏摩尔体积,一般取2.0 cm3/mol[24]。将式(4)代入式(3),可得：

$?=-\mathit{SD}?\left[\frac{\partial ?}{\partial ?}+?\ln ?\frac{\partial }{\partial ?}\left(\ln \left(?-{?}_{\mathrm{Z}}\right)\right)+?\frac{{?}_{\mathrm{H}}}{?(?-{?}_{\mathrm{Z}})}\frac{\partial {?}_{\mathrm{h}}}{\partial ?}\right]$(5)

将式(5)代入式(2),即可得到氢扩散的本构方程为：

$\text{msubsup}\left[\mathit{\delta ?}\left(?\frac{\mathrm{d}?}{\mathrm{d}?}+?\frac{\mathrm{d}?}{\mathrm{d}?}\frac{\mathrm{d}?}{\mathrm{d}?}\right)+\frac{\partial \mathit{\delta ?}}{\partial ?}?\mathit{SD}?\right.$

$\left.\left(\frac{\partial ?}{\partial ?}+\frac{?\ln ?}{\left(?-{?}_{\mathrm{Z}}\right)}\frac{\partial ?}{\partial ?}+\frac{?{?}_{\mathrm{H}}}{?\left(?-{?}_{\mathrm{Z}}\right)}\frac{\partial {?}_{\mathrm{h}}}{\partial ?}\right)\right]\mathrm{d}?={\int }_{?}\mathit{\delta ?q}\mathrm{d}?$(6)

式中,q=-nJ。由于本工作主要研究组织不均匀和残余应力对氢扩散行为的影响,为了简化计算,未考虑温度的变化,因此式(6)可进一步简化为：

${\int }_{?}\left[\mathit{\delta ?S}\frac{\mathrm{d}?}{\mathrm{d}?}+\frac{\partial \mathit{\delta ?}}{\partial ?}?\mathit{SD}?\left(\frac{\partial ?}{\partial ?}+\frac{?{?}_{\mathrm{H}}}{?(?-{?}_{\mathrm{Z}})}\frac{\partial {?}_{\mathrm{h}}}{\partial ?}\right)\right]\mathrm{d}?={\int }_{?}\mathit{\delta ?q}\mathrm{d}?$(7)

此外,其它边界条件、已知条件或基本假设如下：(1) 管线母材及焊接接头各部位的氢扩散系数、氢溶解度采用表2所示氢渗透实验结果;(2) 氢的吸附过程以及逸出过程不受表面效应的影响,即只考虑管线内部的扩散过程;(3) 氢在焊接接头各区均以原子的形式扩散;(4) 焊接接头各区之间满足化学势连续的条件;(5) 管线内壁氢浓度为表2所示焊接接头各区的吸附氢浓度,当氢扩散至管线外表面时会复合成为H2逸出,因而管线外表面的氢浓度为0;(6)设管线壁厚为L,内表面位置为X=0,外表面位置为X=L,扩散时间为t,上述边界条件可表述为：当t=0时,X=0,C=C0 (C0为亚表面氢浓度);0<X≤L,C=0;当t>0时,X=0,C=C0;0<X<L,C=C(t);X=L,C=0。采用瞬态分析的方法,模拟计算管线内部不同位置的氢浓度随时间的变化情况,即C(t),当氢扩散至稳定状态后,各部位的氢浓度将不再变化,在此基础上观察、分析组织不均匀和残余应力对氢分布的影响;(7) 管线内部的压力(总压和氢分压)直接影响焊接接头各区表面的吸附氢浓度,该值已通过氢渗透实验获得,因而模拟计算时不再考虑管线内外压力差的问题。

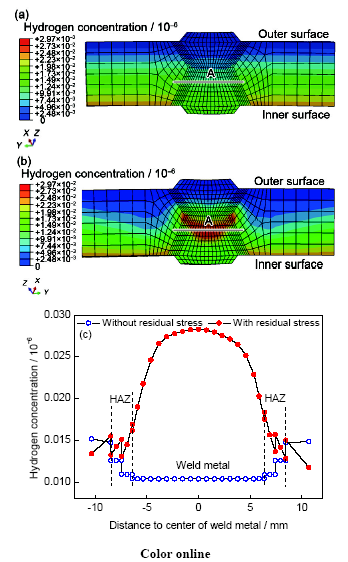
图6为煤制气管线焊接接头中氢扩散至稳态后的浓度分布。其中,图6a为不考虑接头残余应力情况下的氢浓度分布状态,图6b为考虑接头残余应力作用时的氢浓度分布状态。当不考虑残余应力时,氢扩散主要受内外壁氢浓度差异的影响,即氢的扩散方向是由管线内壁的高浓度区域向管线外表面扩散,此时管线内壁接头区域的氢浓度与氢渗透实验所得试样表面吸附氢浓度(表4)相当,即母材的氢浓度最高,其次为部分相变区、细晶区和粗晶区,焊缝区的氢浓度最低。当考虑残余应力的氢富集作用以后(图6b),其影响主要体现在焊缝及周边的热影响区位置,这些区域的氢浓度不再呈现由内表面向外表面梯度降低的规律,最高氢浓度出现在焊缝心部,即静水应力最大的区域。为了精确地分析接头组织变化和焊接残余应力耦合作用对氢浓度分布的影响,沿图6a和b中的路径A所示接头宽度方向读取各有限元分析点的氢浓度,结果见图6c。对于残余应力最高的焊缝中心区域,不考虑残余应力影响时的氢浓度为0.0104×10-6,而残余应力作用下氢的浓度可达0.0283×10-6,氢浓度提高了2.7倍。此外,考虑残余应力的作用下,热影响区位置的氢浓度也有了不同程度的增加。

图6   X80钢焊接接头中的氢浓度分布

Fig.6   Hydrogen concentration distributions in X80 welded pipeline
(a) without residual stress
(b) with residual stress
(c) hydrogen distribution along line A in Figs. 6a and b

为了确定残余应力作用下接头各区所能达到的最高氢浓度,沿管线厚度方向读取焊接接头各区的氢浓度,将各区所能达到的最高氢浓度列于表4。在仅考虑焊接接头组织不均匀的情况下,接头各区的最高氢浓度为管线内表面的吸附氢浓度。考虑与残余应力耦合作用的情况下,接头各区的最高氢浓度均出现不同程度的增加。由此可以确定,X80钢焊接接头中的组织不均匀和残余应力均可诱导氢扩散的发生,其中,残余应力的影响大于组织不均匀性的影响。例如,在不考虑焊接残余应力的情况下,焊缝区的氢浓度最低(表4)。但是由于焊缝区的残余应力最高,其对氢扩散和富集的影响也最大,因而在考虑残余应力的影响后,接头的最高氢浓度出现在焊缝区。

3 氢扩散数值模拟的应用

对于焊接接头而言,氢致失效裂纹极易萌生于氢富集区域,因此,通过数值模拟确定焊接接头的氢富集区,然后在此基础上进行氢富集浓度下的慢应变速率拉伸(SSRT)实验,可以考察氢富集对材料氢致脆化敏感性的影响。鉴于此,本工作提出了等效充氢压力的概念,根据氢扩散数值模拟获得接头的最高氢浓度(Cmax)和根据高压氢渗透实验获得的相应区域的S,然后根据Sieverts定律即可计算得到相应的等效充氢压力(pe)：

${?}_{\mathrm{e}}={\left(\frac{{?}_{\max }}{?}\right)}^2$(8)

根据式(8)计算得到焊缝金属的等效充氢压力,随后进行SSRT实验,并与模拟煤制气环境和N2环境对比,间接反映组织不均匀单独作用或与残余应力耦合作用所致氢富集对材料氢致脆化敏感性的影响。测试设备选用CORTEST P/N LF-100型慢速率拉伸试验机,应变速率为1×10-5 s-1,温度为(40±0.5) ℃。实验完成后,计算得到相应的力学性能参数,根据断面收缩率的损失计算氢脆系数,并采用Nova Nano SEM450型扫描电镜(SEM)进行试样断口分析。

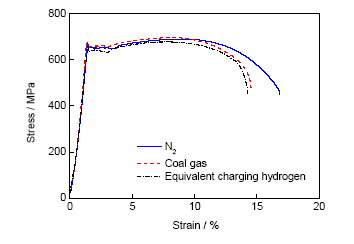
图7为焊缝金属在N2、模拟煤制气以及考虑氢富集的等效充氢压力下的应力-应变曲线,表5为相应的力学性能。可以发现,模拟煤制气环境和等效充氢压力环境并未使得接头各区试样的弹性变形过程受到影响。此外,表5所示拉伸强度也并未出现规律性的变化,抗拉强度的波动可能是由材料自身组织的不均匀性、测量误差以及实验设备自身的误差所致[25]。伸长率和断面收缩率按照N2、模拟煤制气、等效充氢环境的顺序依次减小。采用断面收缩率的损失[15]计算氢脆系数(FH),以表征煤制气环境以及氢富集(等效充氢压力)对焊缝金属氢脆敏感性的影响,结果见表5。

图7   焊缝金属在不同环境下的应力-应变曲线

Fig.7   Stress-strain curves of weld metal in different environments

根据经验判断[26],当氢脆系数不超过25%时,材料在服役环境中基本不会发生氢致失效;当氢脆系数介于25%和35%之间时,存在发生氢致失效的风险;当氢脆系数超过35%时,材料会发生氢致失效。从表5可见,模拟煤制气环境下焊缝区的氢脆系数为18.56%,不会发生氢脆失效;在考虑氢富集的等效充氢压力下,氢脆系数达到32.53%,增加幅度达到75.27%,处于氢脆失效危险区。

图8a~c分别为焊缝金属在N2、模拟煤制气以及等效充氢环境中宏观断口形貌的SEM像。可以看出,试样的断口面积依次增加,相应的断面收缩率不断降低,塑性变形能力逐渐恶化。N2环境中的试样断口呈杯锥状(图8a),属于典型的韧性断裂特征。断口边缘局部放大形貌如图8d所示,可见该区由塑性较好的韧窝组成。模拟煤制气环境下试样断口局部放大形貌(图8e)同样主要由韧窝组成,但韧窝的深度显著减小,说明塑性变形能力有所下降。在考虑残余应力氢富集作用的等效充氢环境下,试样断口边缘(图8f)几乎观察不到塑性变形迹象,断口表面平齐,无韧窝出现,存在一些细小的二次裂纹,氢脆敏感性比模拟煤制气环境下有明显的增加,与氢脆系数的计算结果相对应。

通过氢脆系数和断口分析可知,由焊接残余应力所导致的氢富集对材料的氢脆失效敏感性具有重要影响,采用数值模拟的方法对氢扩散进行数值模拟,进而确定氢富集区域和程度则是焊接接头安全评价的重要基础。

图8   不同环境中焊缝区断口形貌的SEM像

Fig.8   Low (a~c) and high (d~f) magnified fracture SEM images of weld metal in nitrogen gas (a, d), coal gas (b, e) and equivalent charging hydrogen (c, f) environments

4 结论

(1) 综合考虑焊接残余应力和组织不均匀对氢扩散的影响,建立了煤制气输送管线X80钢螺旋焊管氢扩散三维计算模型。结果表明,接头残余应力和组织不均匀性均会导致氢扩散的发生,其中残余应力的影响大于组织不均匀性的影响。残余应力最高的焊缝区心部,其氢浓度比不考虑残余应力时提高了2.7倍。

(2) 提出等效充氢压力的概念,采用SSRT实验研究了组织不均匀和焊接残余应力耦合所致氢富集对氢脆敏感性的影响。焊缝金属的氢脆系数由模拟煤制气环境中的18.56%上升至等效充氢压力下的32.53%,增加幅度达到75.27%。

(3) 残余应力对氢扩散的影响不容忽视,采用数值模拟的方法进行焊接接头氢富集的预测,并与环境力学性能测试相结合,提供了科学评价临氢焊接结构氢致脆化敏感性的新思路。

来源--金属学报