分享：非连续增强铝基复合材料的热变形行为研究进展

肖伯律, 黄治冶, 马凯, 张星星, 马宗义

中国科学院金属研究所沈阳材料科学国家研究中心 沈阳 110016

摘要

关键词： 金属基复合材料 ; 热加工 ; 本构方程 ; 加工图 ; 变形机制

航空航天、电子、核电等领域高技术装备的不断升级,对结构与性能可设计性较强、物理和力学性能优异的金属基复合材料(metal matrix composites,MMCs)需求快速增长,并推动MMCs在陆上运输、体育休闲等普通民用领域的应用。其中,非连续增强铝(discontinuously reinforced aluminum,DRA)复合材料凭借成本和性能的综合优势,已经成为目前应用最广泛的MMCs[1]。DRA复合材料通常是指在铝合金中添加颗粒、晶须等不同形态的陶瓷、金属或碳材料作为增强体而制备得到的铝基复合材料。复合材料中增强相“连续”和“非连续”的界定与剪切滞后模型[2]中纤维状增强体同基体之间的临界载荷传递长度相关。“非连续”是指晶须或短纤维长度要小于5倍临界载荷传递长度,且大于5倍长径比,而颗粒增强相的长径比一般认为是1[3]。

相对于连续长纤维增强铝基复合材料,DRA复合材料具有成本较低、制备工艺简单灵活、各向同性等优点,而且所添加的颗粒或晶须等增强相可以在不发生损伤的情况下协同基体合金的塑性变形,使DRA复合材料在一定变形量下塑性成形。对颗粒增强铝基复合材料,通常在颗粒体积分数不大于40%时可以进行挤压、轧制和锻造等传统的热塑性变形加工[3,4,5,6,7]。然而,在热加工过程中,增强相的添加导致材料变形抗力增大。此外,难变形增强体与基体之间的载荷分布非常不均匀,很容易在应力集中的位置形成孔洞、脱粘、增强体断裂和基体裂纹等内部损伤[8,9]。因此,DRA复合材料相对于未增强铝合金可加工性能显著下降。若热加工工艺选择不当,复合材料制品中很容易产生缺陷,如锻件内部和表面裂纹、轧制板材和挤压棒材的开裂、增强体颗粒带偏聚等[6,10~13]。

热变形行为一直是DRA复合材料研究关注的重点问题。除了避免开裂、孔洞等缺陷形成,通过塑性变形调控DRA复合材料中的增强相分布、晶粒形态等,是获得高性能DRA复合材料零件的基础。过去30年对DRA复合材料的热变形行为开展了大量研究,为DRA复合材料的成形加工提供了基础指导。但DRA复合材料在变形过程中的组织演化行为复杂,因此对DRA复合材料热变形行为的研究方法仍在不断改进,以提高DRA复合材料的组织、缺陷预测精度。本文将从DRA复合材料热变形行为的理论研究方法、铝合金基体的变形机制以及不同类型增强体铝基复合材料的变形特征方面,对DRA复合材料热变形行为的研究进展进行回顾与总结,提出目前研究中存在的问题并展望未来的研究方向。

1 热变形行为的理论研究方法

对于金属材料热变形行为,目前应用比较广泛的理论研究方法主要是建立本构方程和加工图,此外,有研究者[9,14,15]通过应变速率敏感指数和温度敏感指数对材料热变形机制进行研究,也获得了一定成效。以下简要叙述了这几种方法在DRA复合材料热变形行为研究中的应用。

1.1 本构方程

本构方程描述了材料在外加载荷下的力学行为。材料力学性质研究的重要任务之一就是构建材料在不同载荷条件下的力学响应本构模型。例如,金属在热加工、超塑性、蠕变以及冲击载荷等变形条件下所表现出不同性质的力学行为,都可以由相应的本构模型来进行描述。

DRA复合材料在热加工过程中的流动行为通常比较复杂。加工硬化或应变软化行为对应变速率、温度和应变等因素较敏感,因此可以从本构方程反应DRA复合材料中的组织演化过程,对DRA复合材料的热加工工艺(如锻造、轧制、挤压等)的设计和加工设备的选择提供依据,还可以为有限元模拟提供基本参数。按照研究关注程度划分,可以分为2类：唯象或物理本构模型和动力学本构模型。

1.1.1 唯象或物理本构模型 唯象本构模型是基于经验公式对流变应力进行描述,其函数式中的参数通常没有明确的物理意义。常见的唯象本构模型有Johnson-Cook (JC)模型[16]、Bodner-Partom (BP)模型[17]、Fields-Backofen (FB)模型[18],以及Khan等提出的一系列本构模型,包括Khan-Huang (KH)[19]、Khan-Huang-Liang (KHL)[20]、Khan-Liang (KLF)[21]和改进的Khan-Huang-Liang模型(M-KHL)[22]等。由于唯象本构模型参数少、方程形式简单且易于求解,建立的可描述材料在较宽载荷条件下力学响应的本构模型,适合于嵌入计算程序中进行损伤、冲击以及大塑性变形等力学过程的有限元仿真计算[23,24]。

基于位错动力学的物理本构模型理论[25,26,27]认为,在扩散、蠕变机制不占主导的温度和应变速率条件下,金属材料的塑性变形基本上通过位错运动来实现。宏观的流变应力,实质上反映了材料对位错运动过程的阻碍,因此可以基于位错运动机制来描述金属在较宽温度、应变速率区间的力学响应。位错在运动过程中除晶格本身固有的阻碍以外,按照作用方式的不同还会受到2种类型的阻碍,分别为短程势垒和长程势垒。短程阻碍可以通过热激活而克服,而长程阻碍则与温度无关。

由于DRA复合材料在工业领域的应用远不如传统金属材料,而且发展历史相对较短,因此DRA复合材料的唯象本构模型和物理本构模型的研究鲜见报道。关于唯象本构模型的报道,仅有Shafieizad等[28]构建了描述Mg2Si/Al-Cu复合材料高温变形行为的JC本构模型,发现在远离计算参考温度和参考应变速率的条件下,JC模型的计算结果与实验应力-应变曲线偏差较大。实际上,由于增强相的存在,DRA复合材料的变形行为更加复杂,因此较简洁的唯象本构模型计算精度会受到影响;而物理本构模型依赖于对位错运动过程的响应,DRA复合材料中位错与析出相、增强相、晶格的交互作用复杂,使得计算较困难。这些可能也是导致这2个模型较少应用于DRA复合材料研究的原因。

1.1.2 动力学本构模型 动力学本构模型是最早由Sellars和McTegart[29]提出的Arrhenius方程,该模型认为应变速率受到热激活过程控制。Arrhenius方程不仅可以对流变应力与温度、应变速率、应变之间的函数关系进行描述,还可以计算与变形机制相关的一些物理参数(如应力指数(n)、门槛应力(σo)和变形激活能(Q)),因此,也可以被看作是一种动力学本构方程。凭借其普适性,Arrhenius方程在DRA复合材料的蠕变、超塑性、热加工变形行为研究中[30,31,32]应用最广泛。

在进行铝合金及DRA复合材料的蠕变或超塑性变形机制研究时[33,34,35,36,37,38,39],通常认为n的大小对应不同的变形机制,并且选取整数n来计算σo。在蠕变条件下n与变形机制的对应关系为[33,34,36]：n=2,晶界滑动;n=3,黏滞滑移;n=5,高温位错攀移;n=7,低温攀移;n=8,晶格扩散控制的蠕变。门槛应力由位错与细小硬质颗粒之间的相互作用而形成,其形成机制主要有4种模型[36]解释：(1) Orowan应力,位错在颗粒间的弓出所需要的应力[40];(2) 局部攀移力,使位错长度增加而可以攀移过颗粒的额外背应力[41];(3) 脱附力,攀移后的位错从非连续颗粒脱离所需的应力[42];(4) 位错分解力,晶格位错分解为可以进入到基体与颗粒界面并发生攀移的位错所需要的力[43]。可见,上述机制一般是基于位错绕过细小沉淀相或颗粒,但是由于DRA复合材料中颗粒、晶须和短纤维增强相的尺寸较大(μm量级),Orowan机制并不适用,而另外3种机制的作用形式也与只存在沉淀相时有一定差异。Mohamed等[33]认为,DRA复合材料的蠕变特征与弥散强化合金相似,可以通过蠕变门槛应力解释,计算得到非连续增强体所引入的门槛应力值要小于实验估算值。Mishra等[37]在Si3N4/2124Al进行高应变速率超塑本构方程研究时,选取真应力指数n=2 (颗粒尺寸0.2 μm)来计算门槛应力,发现随着温度升高σo逐渐减小,当温度高于500 ℃时σo接近于0;超塑性门槛应力值还与颗粒形状和尺寸相关,晶须增强复合材料的σo最大。Kaibyshev等[39]对15%SiCw/2009Al (体积分数)的热压缩变形行为进行研究,选取n=3求解σo可以获得较好的线性相关性。

在进行金属高温变形过程分析时,Arrhenius方程求解得到的激活能Q通常表示与原子机制相关的势垒大小。依据Arrhenius方程,由流变应力(σ)自然对数与温度(T)倒数(lnσ-1000/T)的数据线性回归斜率可以计算得到表观变形激活能(Qa)。表1[44,45,46,47,48,49]列出了部分DRA复合材料的热加工表观变形激活能。通过对比可以发现,对于同一复合材料体系,随着增强相含量增加,Qa升高;在增强相体积含量相同时,较小的增强相尺寸通常对应较高的Qa;在高温下对应的Qa较高。粉末冶金制备工艺通常会引入氧化物颗粒,对应复合材料的Qa要高于搅拌铸造法制备的复合材料。此外,基体中添加固溶元素也将提高复合材料的Qa。因此,可以认为DRA复合材料的Qa高低通常与变形抗力的变化相关,促使变形抗力增加的因素都有可能引起Qa升高。

在许多铝合金和DRA复合材料热变形本构的研究[33,38,50~54]中,采用归一化应力(即应力与模量随温度变化函数E(T)或G(T)的比值)的方法来尝试求解门槛应力σo和真实激活能Qc。但对模量与温度的数学关系并不统一[33,38],而多数文献[50,51,52,53,54]中应用的经验公式,普遍与实测值[55,56]存在很大偏差。将剪切模量换算为弹性模量,得到模量随温度变化的经验公式与实测数据之间的对比如图1所示。可以看出,在高于200 ℃时铝合金模量随温度升高急剧降低,多数文献[50,51,52,53,54]所使用经验公式中铝合金及纯Al的模量随温度升高变化缓慢降低,显然与真实的模量温度关系不符。而如果以铝合金实测模量计算通常会得到负的Qc,无法通过Qc得到热变形的实际物理意义。因此,对铝合金和DRA复合材料难以通过Qc计算预测变形机制。

图1   铝合金弹性模量随温度变化的经验公式与实测值对比

Fig.1   Comparison of Young's modulus varying with temperature between the empirical equations and the experimental data in Al alloys

尽管本构方程对DRA复合材料变形机制的预测较困难,但过去大量的研究通过本构方程揭示了DRA复合材料热加工时流变应力与温度、变形速率以及应变等变形条件的关系,并通过多种经验公式对其进行了数学描述。通过与未增强铝合金的比对,本构方程是最早揭示DRA复合材料复杂流变行为的依据。由于本构方程构建了流变应力与变形条件之间的数学关系,可以为DRA复合材料零件成形加工时的流变场(应力、应变与温度场等)构建提供基础数据。如果进一步引入损伤准则,还可以建立零件成形加工损伤场,从而对DRA复合材料的零件成形工艺制定提供依据[11]。因此,建立完善准确的本构方程,是推动DRA复合材料变形加工技术发展的基础。

1.2 加工图

加工图理论从能量转化角度分析金属材料热变形行为中的组织演化,与经典动力学方法所采用的经验本构方程不同,它基于动态材料模型(dynamic materials model,DMM)构建,适合较复杂的材料体系,避免了因激活能复杂而难以分析变形机制的困难[57]。DMM将材料作为一个能量耗散体,单位体积吸收的瞬时总能量P (变形加工设备输入能量)由2种方式所耗散,分别为耗散量G和耗散协量J。G表示塑性变形所耗散的能量,绝大部分由位错运动生热消耗,余下的一小部分以晶界缺陷形式存储;J表示材料内部由微观组织转变所耗散的能量,包括动态回复(dynamic recovery,DRV)、动态再结晶(dynamic recrystallization,DRX)、晶界滑动(grain boundary sliding,GBS)、相变以及裂纹形成等。

DMM中假定流变应力与应变速率之间满足幂率本构关系[57,58],在应变速率敏感指数m=1的理想条件下J将达到最大值Jmax,这样功率耗散系数(η)可由下式求解：

$?=\raisebox{1ex}{$?$}\!\left/ \!\raisebox{-1ex}{${?}_{\max }$}\right.=\raisebox{1ex}{$2?$}\!\left/ \!\raisebox{-1ex}{$(?+1)$}\right.$(1)

考虑大塑性流动条件下的Zigler's失稳条件,可以得到DMM对应的失稳准则：

$?=\frac{\partial \ln \left(\raisebox{1ex}{$?$}\!\left/ \!\raisebox{-1ex}{$(?+1)$}\right.\right)}{\partial \ln \dot{?}}+?<0$(2)

式中,ξ为失稳因子, $\dot{?}$为应变速率。

在DMM中,只有当应力与应变速率满足幂率关系时,η的求解公式(1)才成立。然而,大多数材料体系很难严格遵循幂率关系式,这样计算得到的η将产生误差。随后,Murty等[59]修正了DMM中G的求解方法,提出了改进的动态材料模型(modified DMM,MDMM),将G的求解分成2部分：

$?={\int }_0^{{\dot{?}}_{\min }}?\mathrm{d}\dot{?}+{\int }_{{\dot{?}}_{\min }}^{\dot{?}}?\mathrm{d}\dot{?}={\left(\frac{?\dot{?}}{?+1}\right)}_{\dot{?}={\dot{?}}_{\min }}+{\int }_{{\dot{?}}_{\min }}^{\dot{?}}?\mathrm{d}\dot{?}$(3)

式中, ${\dot{?}}_{\min }$为最小实验应变速率,在应变速率小于 ${\dot{?}}_{\min }$的范围内,依然假定满足幂率关系;而在应变速率大于 ${\dot{?}}_{\min }$的范围内G由拟合的应力-应变数据曲线积分求得。相应地,在特定应变和温度下η的计算式写作：

$?=\raisebox{1ex}{$?$}\!\left/ \!\raisebox{-1ex}{${?}_{\max }$}\right.=\frac{?}{\raisebox{1ex}{$?$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}=2{\left(1-\frac{?}{?}\right)}_{?,?}$(4)

式中,ε为应变。同样,适用范围更广的失稳准则公式为：

$?\mathrm{\text{'}}=\frac{2?}{?}-1<0$(5)

式中,ξ′为失稳因子,通常,MDMM可以获得更精确的计算结果。

由于DRA复合材料的难加工性以及热变形过程中组织演化的复杂性,DMM提出不久之后便被应用到DRA复合材料的热变形行为研究[60,61,62]。Bhat等[60]最早将加工图理论应用于DRA复合材料热变形机制的分析,分别绘制了粉末冶金法制备和经后续挤压加工2种工艺制备的10%SiCp/1100Al (体积分数)复合材料的功率耗散系数图。结合微观组织观察发现,粉末冶金制备的复合材料,动态再结晶机制发生在500 ℃、0.01 s-1参数下,对应η=30%;而经挤压加工后产生的细晶结构促使晶界迁移能力增强,导致动态再结晶机制开动的温度降低而应变速率有所升高,发生在425 ℃、1 s-1参数下;2种材料在300 ℃、0.001 s-1条件下均发生了动态回复,对应η=21%。

加工图中耗散系数常会出现多个峰值区。Kai等[63]对原位反应法制备5%ZrB2/2024Al (质量分数)纳米复合材料的热压缩变形行为进行了研究,认为耗散系数较高的主峰值区域对应的变形机制为完全的DRX,在该区域的加工参数下变形比次峰值区域更不易产生缺陷。基于DMM和MDMM的差别,Xu等[64]以挤压铸造法制备20%SiCw/6061Al (体积分数)复合材料为对象分别构建了加工图,并以Gegel's稳定准则绘制了失稳图。结果发现Prasad和Murty失稳准则[57,59]预测结果与实际情况较为一致,但预测的失稳区要略小于出现热压裂纹试样所对应的参数范围,而Gegel's稳定准则预测的失稳区则与实际情况偏差较大。

通常,η升高表明在变形过程中材料以冶金方式耗散的能量增多,而以变形生热方式消耗的能量减少。对以往的文献[65,66,67]进行总结可以发现,铝合金发生DRV通常所对应的η为10%~27%,变形参数位于温度300~500 ℃和应变速率0.001~1 s-1范围内;而DRX所对应的η略高,为25%~38%,变形参数位于温度400~550 ℃和应变速率0.01~1 s-1范围内。对DRA复合材料,增强相的加入通常会导致η降低,其DRV一般发生在温度区间300~400 ℃和应变速率0.001 s-1,对应的η在10%~25%范围内[60,68];而DRX一般发生在温度400~450 ℃和应变速率0.01~1 s-1热变形条件下,对应的η范围在21%~30%[68,69,70,71]。在高温下,DRA复合材料对应的η峰值区通常与晶界滑动变形机制相关[61]。

通常加工图是在特定应变下构建的,如果要表征能量耗散系数随应变的连续变化,需要构建一系列不同应变的加工图。通过数据处理,不同学者[72,73,74,75]构建了Al、Mg、Ti合金以及复合材料的三维加工图。Mokdad等[74]绘制的碳纳米管(CNT)增强复合材料(2.0%CNT/2024Al,质量分数)三维功率耗散系数图如图2[74]所示。三维加工图克服了在单一的二维加工图中无法考虑应变影响的不足,可以从整体上反映出材料在温度、应变速率、应变全参数、全水平的三维空间热加工性能。但在借助加工图分析不同变形参数下的变形机制时,二维加工图则较为直观便捷。

图2   2.0%CNT/2024Al (质量分数)复合材料的三维加工图[74]

Fig.2   3D power dissipation coefficient (η) maps of 2.0%CNT/2024Al (mass fraction) composite at temperatures of 200, 300 and 400 ℃ (a), strain rates of 0.001, 0.01 and 0.1 s-1 (b)[74]

1.3 应变速率和温度敏感指数

在材料的热加工过程中,应变速率和温度是2个关键的加工参数,对材料微观组织演化影响最显著。变形加工时,位错运动方式、空位(点缺陷)浓度、晶界迁移速率、固态相变等影响塑性变形机制的因素都与温度密切相关,这些因素随温度的变化表现为流变应力的变化。在高温(约0.8Tm,Tm为熔点)下,变形机制为位错攀移、空位的定向扩散及晶界滑动等,这些行为是受到热激活控制、以扩散为主导的。扩散相关的变形机制不仅受温度变化控制,而且受应变速率变化的影响较大,应变速率的大小决定了扩散变形机制对总塑性变形的贡献大小。

基于上述原因,可以通过流变应力的应变速率敏感指数(m)和温度敏感指数(s),来确定热变形过程中微观组织演化机制的转变,从而对目前仅以加工图中的η作为变形机制判据进行补充验证。

1.3.1 应变速率敏感指数 在蠕变、超塑性以及热加工过程中[32,76,77],若应力与应变速率之间近似满足幂函数本构关系,则m可以定义为lnσ对ln $\dot{?}$的偏导数：

${\left(\frac{\mathrm{d}?}{\mathrm{d}?}\right)}_{?,?}={\left(\frac{\dot{?}\mathrm{d}?}{?\mathrm{d}\dot{?}}\right)}_{?,?}={\left(\frac{\partial \ln ?}{\partial \ln \dot{?}}\right)}_{?,?}={\left(\frac{\partial \lg ?}{\partial \lg \dot{?}}\right)}_{?,?}=?$(6)

其表观物理意义为流变应力在某一应变速率附近的变化率,即对应变速率变化的敏感性,m越大表明流变应力对应变速率的敏感性越高。m通过实验数据拟合的ln σ-ln $\dot{?}$曲线斜率确定,通常由三次样条插值法拟合得到的曲线准确性更高[9]。

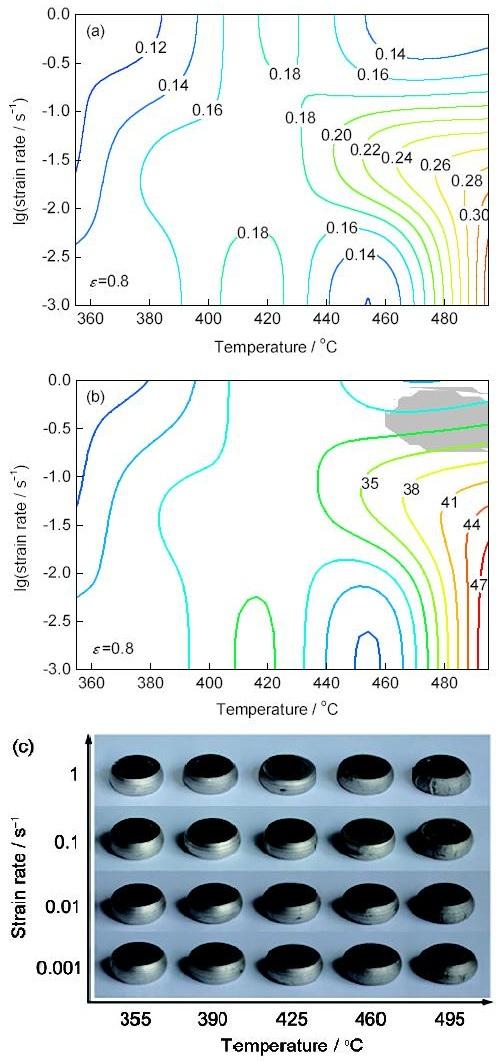
在DMM中m还表示G与J之间的功率分配系数[57],如式(6)中第一项所示,m与η的物理意义相近。通过对比14%SiCp/2014Al (体积分数)复合材料的η图和m图(图3[9])可以发现,这2个参数随温度和应变速率的变化趋势非常相似,在钛合金、钢中也发现类似的结果[14,78]。在低应变速率下,扩散相关的塑性变形机制有足够的时间充分进行。从图3a[9]中可以看到,m总体上在0.1~0.3范围内变化,在高温低应变速率区域m表现为较大值,在m>0.3时,变形机制以超塑性变形为主[79]。与m图不同,图3b[9]所示加工图的不同区域(不同η的数值)能揭示动态回复、动态再结晶以及晶界滑动等变形机制。根据图中区域对应的变形参数对相应的试样进行解剖,可以通过金相组织验证变形机制。另外,尽管m与η图均可对复合材料的流变行为进行预测和描述,但m图并不能直接预测变形损伤。相比之下,加工图则可以进行变形损伤的预测。

图3   14%SiCp/2014Al (体积分数)复合材料的应变速率敏感指数(m)图与加工图及其预测的流变失稳区域中的试样损伤[9]

Fig.3   Contour map of strain rate sensitivity index (m) (a) and processing map (b) for 14%SiCp/2014Al (volume fraction) composite at true strain of 0.8, grey area up right corner in (b) denotes flowing instability which resulted in damage of specimens at higher strain of 0.9 (c)[9]

图3b[9]所示的加工图中右上角灰色区域为通过MDMM模型预测的流变失稳区域,在此区域所对应的工艺参数下进行热变形压缩时,复合材料易于产生流变失稳,主要表现为裂纹形成。图3c[9]是复合材料压缩真应变达到0.9时样品表面形貌。不难发现,图3c[9]中右上角区域对应的参数下,试样表面均出现肉眼可见的裂纹,与加工图中所预测的流变失稳区域非常吻合。该结果体现了加工图预测损伤方面的便捷与可靠性。

1.3.2 温度敏感指数 Malas[80]基于热力学第二定律,推导出一个用于评价温度对材料变形行为及可加工性影响的无量纲参数,即s,其表达式如下：

$?={\left[-\frac{1}{?}\frac{\partial \ln ?}{\partial \left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$?$}\right.\right)}\right]}_{\dot{?},?}$(7)

依据热力学第二定律,在稳态流动条件下材料存储熵的速率应该高于变形热的熵产率,这时s应大于1。许多文献[81,82,83,84,85]中将s用于计算由Lyapunov函数推导而得到的材料流变失稳判据。由于温度对流变应力的影响通常与热加工过程中的微观组织演化机制相关,因而s随温度和应变速率的变化还可以反映特定条件下微观组织和变形机制的转变。

图4[9]为搅拌铸造后挤压的14%SiCp/2014Al (体积分数)复合材料的温度敏感指数图。依据s的变化趋势大致可以划分为3个温度区间。在I、III区间(Range I、III)内,s随着应变速率的降低而增大。尤其在III区间,s随温度的升高而增大,并在温度470~495 ℃和应变速率0.001~0.01 s-1位置出现了峰值。这表明在低应变速率和高温条件下,流变应力对温度的变化更加敏感。而在II区间,s呈现较低值且随着温度增加而出现波动,通过微观组织观察发现此区间内440 ℃下发生异常晶粒长大。实际上,在II区间的局部区域s已经达到了Gegel等[81]所提出的失稳条件(s<1)。

图4   14%SiCp/2014Al (体积分数)复合材料在应变量0.8时的温度敏感指数(s)图[9]

Fig.4   Contour maps of temperature sensitive index (s) for 14%SiCp/2014Al (volume fraction) composite at true strain of 0.8[9]

本构方程与加工图方法提供了复合材料热变形行为的经验模型,它们反映了流变应力随温度等变形条件变化的差异,在物理化学理论上建立起流变行为与工艺因素的关系。相比本构方程研究,加工图方法能更可靠地预测热变形参数对DRA复合材料的变形行为影响,显示出较高可靠性。然而,由于增强相与基体合金性质差异巨大,因此DRA复合材料不同微区内(如界面附近与远离界面区域)的变形行为必然存在差异,这也是影响本构方程和加工图可靠性的重要原因。因而本构方程和加工图研究离不开微观组织观察验证,这也是DRA复合材料热变形研究的重要内容。

2 DRA复合材料热变形行为特征

在DRA复合材料中,塑性变形主要由基体合金来实现,而增强体会对变基体合金的变形行为产生影响。因此,工艺参数对DRA复合材料变形机制的影响不应直接沿用未增强铝合金的研究结果。开展DRA复合材料中铝合金的变形机制和组织形成原因研究,有助于优化DRA复合材料的热加工工艺,避免热加工缺陷和损伤的出现。

2.1 动态回复

Al属于高层错能金属(约166 mJ/m2)[86],位错较容易进行攀移和交滑移,在高温下倾向于发生动态回复。这种变形机制以位错运动为主[87],与静态回复过程相似,动态回复也会形成低角晶界。同时,外加载荷也将促使低角晶界发生迁移,迁移过程导致部分异号位错湮灭。而在动态回复过程中,细小的亚晶仍然保持近似等轴状[88],随温度升高亚晶尺寸增大且胞壁厚度减小,而高角晶界不会发生迁移。通常,会在大晶粒内部形成大量尺寸均匀的细小等轴亚晶[89]。如图5a所示,动态回复机制主导的变形条件下,在17%SiCp/2009Al (体积分数,下同)复合材料热压缩试样的剪切变形区,沿剪切方向排列的大晶粒内部形成了许多近似等轴状的亚晶(红色线)。透射电镜(TEM)像进一步清晰地显示出大晶粒内部的亚晶和位错胞结构,如图6a所示。

图5   17%SiCp/2009Al (体积分数)复合材料在压缩变形后(ε =0.7)剪切变形区的电子背散射(EBSD)图

Fig.5   EBSD image in shear deformation region of 17%SiCp/2009Al (volume fraction) composite compressed at 400 ℃ and 1 s-1 (a), and 500 ℃ and 1 s-1 (b) with ε =0.7 (Low angle boundaries 2°~15° are marked by red lines, high angle boundaries ≥15° are marked by black lines, SiC particles are shown by black)

图6   17%SiCp/2009Al (体积分数)复合材料压缩变形后(ε =0.7)压缩变形区的TEM像

Fig.6   TEM images in compressive deformation region of 17%SiCp/2009Al (volume fraction) composite compressed at 400 ℃ and 1 s-1 (a), and 500 ℃ and 1 s-1 (b) with ε =0.7 (DRX—dynamic recrystallization, SG—subgrain)

Gholinia等[86]总结了亚晶尺寸与应变和温度之间的关系,认为随应变增加,亚晶尺寸基本上保持恒定,而晶粒尺寸(高角晶界)随应变增加而逐渐减小,在真应变约为2时与亚晶尺寸接近,达到了亚晶极限尺寸。此后晶粒尺寸不再随应变量的增加而发生显著变化。而晶粒和亚晶尺寸均随温度升高而显著增大,但晶粒增大的幅度要大于亚晶。

DRA复合材料中的基体在动态回复变形机制下形成的晶粒特征与铝合金中的情况类似,晶粒尺寸不随应变变化,而形成较多亚结构与晶胞。但实际上DRA复合材料在热加工过程中几乎不会发生单纯的动态回复机制变形,这主要是由于硬质增强相附近的基体合金易于产生因应变梯度而形成的几何必须位错(geometrically necessary dislocations,GNDs),增加了再结晶形成的驱动力,DRA复合材料在发生动态回复为主的变形时,通常伴随动态再结晶晶粒形成。如图6a所示,尽管在400 ℃和1 s-1条件下17%SiCp/2009Al复合材料变形机制以动态回复为主,但界面附近仍可观察到少量再结晶晶粒,其内部呈现无位错的特点。该结果说明,增强相会引起复合材料局部变形行为差异,在同样压缩条件下,试样不同区域内的变形机制并不唯一。

2.2 动态再结晶

变形条件达到高角晶界迁移的条件(如高温或高应变速率)后,就可以发生动态再结晶。Bhat等[60]认为动态再结晶后重构的晶界结构,有利于修复DRA复合材料中因制备过程形成的原始孔洞缺陷。动态再结晶会使流变应力降低,被认为是DRA复合材料热加工的最优条件[60,63,64]。但动态再结晶组织的强度一般要低于动态回复组织。按照新晶粒生成方式的不同,动态再结晶可以分为非连续和连续动态再结晶。

(1) 非连续动态再结晶

非连续动态再结晶一般为在高密度位错处新生成晶粒,其内部位错密度随变形逐渐升高,从而减小晶粒继续长大所需的驱动力,且晶界处的形核也会阻碍新晶粒长大。而当原始晶粒尺寸较大时,新生成的晶粒将在原始晶界处呈链状分布。对于变形过程中位错很难发生滑移和攀移的材料,例如低层错能且滑移系较少的镁合金[90,91]、Ni3Al金属化合物[92]以及孪生诱导塑性变形(TWIP)钢[93,94],非连续动态再结晶通常为主要的变形机制。DRA复合材料中由于界面附近形成大量几何必须位错,是非连续动态再结晶产生的区域。

(2) 连续动态再结晶

按照组织演化机制的不同,连续动态再结晶又可以分为晶体旋转再结晶和几何动态再结晶。晶体旋转再结晶的组织演化机制是,在变形过程中原始高角晶界附近的亚晶发生渐进旋转,并形成从晶粒中心到边缘处的取向差梯度,而在原始晶粒的心部不会出现亚晶。晶体旋转再结晶多发生在滑移较少的镁合金[95]和存在溶质拖拽作用的Al-Mg合金中[96]。而对于大多数铝合金及其复合材料[97,98,99],在热加工条件下通常的再结晶机制为几何动态再结晶。其表现为,当动态回复过程中高角晶界演变成锯齿状,而锯齿大小与亚晶尺寸相近时,若在截面竖直方向发生较大压缩变形,则原始的晶粒将会变得扁平。因为高温变形过程中亚晶尺寸几乎与应变量无关,而在垂直压缩方向上的晶粒厚度将随应变增大而逐渐达到亚晶尺寸,同时高角晶界比例也逐渐升高[86]。这种连续动态再结晶机制多发生在DRA复合材料中,如图5b所示,在连续动态再结晶机制主导的变形条件下,17%SiCp/2009Al复合材料试样的压缩变形区局部区域中,形成了许多细小等轴晶粒,并且其大小与亚晶尺寸相近。图6b所示的TEM像证实了再结晶的发生,其中多数晶粒已长大,少量晶界呈锯齿状(图中左上角),与非连续动态再结晶特征相符。

2.3 增强体对基体组织演化的影响

DRA复合材料在热变形过程中基于位错或亚结构的微观组织机理研究仅见于早期的一些文献[44,45,100~102],而近年的研究[46,48]多集中于热变形参数对其变形行为的影响。由于复合材料微观非均匀的组织特性,很难对其变形机理进行一概而论的描述,而对其微区组织演化的精确捕捉十分困难。

在DRA复合材料的变形过程中,硬质颗粒与基体间会存在局部的应变不协调,需要生成大量几何必须位错来协调变形[103]。而大量几何必须位错和低角晶界,通常也将伴随着较大的取向梯度和较高的存储能。此外,有学者[104]认为,颗粒附近的基体中存在一个变形区,变形区内的位错密度较高且晶格取向差大,从而引发颗粒诱导形核(particle stimulated nucleation,PSN)。由此引起的再结晶起始于变形区内的亚晶,并不总是在颗粒与基体的界面处。

Humphreys等[100]发现SiC颗粒含量较低时(5%,体积分数),复合材料与未增强合金的微观组织相近;而较高SiC颗粒含量(10%,体积分数)有利于获得细小的再结晶组织。当颗粒尺寸大于1 μm时PSN机制易于发挥作用,但需满足2个条件：第一,颗粒附近必须形成变形区;第二,基体中必须有足够高的存储能来提供晶核远离于颗粒长大。对于DRA复合材料,变形区的形成是决定因素。增强相含量不高时,PSN机制会与其它的再结晶机制相互竞争。在高温条件下,颗粒周围的位错可以通过攀移而显著地降低累积程度,因而颗粒诱导形核很难成为主导的再结晶机制。

对颗粒体积分数较高的DRA复合材料,应考虑2种作用对PSN机制的影响[101]：一是由于滑移变形集中在颗粒之间的基体,使局部应变速率高于宏观应变速率;二是间距较近的2个颗粒附近的变形区有可能发生重叠,在变形过程中2个颗粒可以被当作一个更大的颗粒,同样会引起应变和应变速率的不均匀。这2种情况都会促进颗粒诱导形核机制开动。此外,在高温退火条件下,增强体颗粒会对晶粒长大产生阻碍作用。

DRA复合材料的流变应力比未增强的基体合金要高,源于增强相对周围基体的几何约束作用[102],动态回复和动态再结晶则使流变应力下降产生软化,从而使DRA复合材料得以持续变形。增强相含量提高使DRA复合材料加工硬化变得显著。如果在较低温度下,动态再结晶进行不够充分,而DRA复合材料产生以动态回复机制为主的变形时,快速的加工硬化会使位错密度提高,导致DRA复合材料的高温延伸率大幅下降[45]。同时,在增强相引起的应力集中作用下,将形成孔洞并贯通,引起颗粒与基体脱粘以及损伤。

增强相是引起DRA复合材料微区变形不均匀性的重要原因,增强相周边通常出现多种变形方式,使变形组织不再显示出单一化特点,同时也是缺陷形成的主要区域。这也加大了DRA复合材料的变形工艺设计难度。由于增强相的尺寸、含量、形貌是影响组织和缺陷的关键因素,因此掌握不同种类的DRA复合材料可加工性必不可少。

3 不同增强体铝基复合材料的热加工性

DRA复合材料热加工后增强相分布和基体合金组织结构都会发生改变,导致物理、力学性能变化。DRA复合材料的塑性流动过程中增强体与基体之间的载荷分布极不均匀,同一增强体周围不同位置的基体应力状态有可能差异很大,而塑性变形在应力最大的位置优先发生[105]。这将导致DRA复合材料热加工过程中很容易在应力集中的位置发生界面脱粘、增强体断裂,并在基体中形成孔洞、裂纹等损伤。因此控制金属基体不发生快速加工硬化,可以避免过早在增强相附近形成损伤,而且能降低基体流变应力来减小对增强相本身的损伤。

3.1 颗粒增强铝基复合材料

由于颗粒的长径比较小(接近于1),因此热加工过程中增强体受到的损伤相对较小。因此,在高温和低应变速率下不易形成损伤,并可以修复坯锭原有的孔洞,从而提高复合材料的力学性能[106]。DRA常用的增强颗粒包括SiC、B4C、Al2O3等,其中SiC、B4C颗粒呈多角形,变形加工时尖角易于破碎形成尺寸更小的颗粒,并在随后的变形加工中与基体合金形成新的界面,一般不会对力学性能造成负面影响。

如果在较高温度下变形,颗粒受到载荷较小,因而破碎程度较轻,即使在较大变形量下也不会发生明显破碎。而大变形量通常有利于改善颗粒分布[107]。利用该特点,可以通过适当的变形比提高DRA复合材料的力学性能[108]。但过高的变形比(例如挤压比达到40∶1以上)下会发生晶粒长大以及SiC与基体界面的破坏[109]。Pakdel等[12]发现,在低温下增大挤压比导致的颗粒破碎和微观孔洞多聚集在较大增强体颗粒周围,会降低力学性能,而升高温度和减小挤压比有助于降低颗粒的破碎程度;此外,在高挤压比下温度对孔隙率影响较小,此时进行低速挤压有利于提高致密化水平。

3.2 晶须增强铝基复合材料

晶须增强铝基复合材料在锻压加工时,温度和应变速率对晶须的断裂和取向影响显著[110,111]。在高温下基体容易变形,使得晶须容易转动,基体传递到晶须的载荷较小,因而晶须不易断裂。应变速率升高则增大晶须破断比例,所形成的微孔隙不容易被硬化的基体所填充,而扩展为宏观裂纹。高温和高应变速率结合时,晶须增强复合材料热锻工艺性和流变稳定性改善,这主要是由于断裂的晶须易于旋转,铝合金基体较易于流动填充晶须断裂后形成的孔洞和裂纹[111]。Zhao等[112]通过在Al18B4O33晶须增强体表面涂覆SnO2涂层,由界面反应引入低熔点的Sn相,热变形时对界面具有润滑作用,从而实现了在300 ℃下的中低温挤压加工,提高了强度和延伸率。值得说明的是,在热加工过程中,晶须的断裂将导致DRA复合材料中载荷传递强化机制的作用变弱,从而降低复合材料的室温强度。

除了使晶须断裂,挤压还可以改变晶须的分布和取向性,较高的挤压温度有利于晶须在基体中的均匀分布。挤压后发生取向变化的晶须数量主要取决于挤压模具的几何形状和材料的塑性流动特征,而晶须取向的差异受挤压温度的影响较大,挤压温度升高会导致晶须与挤压方向取向差缩小[113,114]。关于挤压比对晶须增强复合材料结构和性能的影响,Hong等[115]的研究表明,在挤压比由10∶1升高到25∶1时SiC晶须沿挤压方向的排列更规整,但晶须的长径比下降。从有效载荷传递角度,晶须的取向与长径比对增强效率的作用相反,因此挤压比为15∶1时可以获得最高的拉伸强度,归因于晶须取向与长径比在此条件下达到了有效的平衡。

3.3 纳米碳增强铝基复合材料

纳米碳主要包括碳纳米管(carbon nanotube,CNT)和石墨烯(graphene,GR)等。相比纳米陶瓷颗粒,纳米碳具有更优异的物理和力学性能,而且具有柔性、长径比高等特征,被认为是DRA复合材料的理想强化相,甚至有望替代现有的陶瓷增强铝基复合材料。然而,由于纳米碳材料在铝合金基体中难以分散均匀,而且界面反应复杂,目前研究主要集中于纳米碳增强铝基复合材料的制备工艺,而对其热加工变形行为的关注相对较少。

纳米碳增强铝基复合材料沿用了典型的DRA复合材料制备工艺,主要包括粉末冶金制备、锻造、轧制或挤压等二次加工[74,116~118],以改善碳纳米管或石墨烯的分散性,并增强界面结合强度。在经过热加工后,纳米碳易于受到损伤。损伤可以通过Raman光谱进行评价[116,119],以G峰与D峰强度比值(IG/ID)来表征纳米碳的损伤程度。Kwon等[119]采用放电等离子烧结及后续热挤压加工(挤压温度400 ℃,挤压比20∶1)制备了CNT/Al复合材料,其Raman光谱测试结果显示,相比于烧结态复合材料,经热挤压后CNT的Raman谱图特征峰未发生明显变化,表明挤压加工对复合材料中CNT造成的损伤很小。

Liu等[117]研究了热轧对CNT/2009Al复合材料中碳纳米管取向的作用,发现轧制后基体中的碳纳米管多数沿轧制方向排列(图7[117]),相比未经轧制的CNT呈随机分布的复合材料,其抗拉强度、延伸率、弹性模量均显著升高。其性能提高主要归因于高长径比的CNT沿轧制方向排列,使载荷传递效率大幅提升。

图7   轧制前后的1.5%CNT/2009Al (体积分数)复合材料中的CNT形态[117]

Fig.7   Morphologies of CNT in 1.5%CNT/2009Al (volume fraction) composite before (a) and after (b) rolling[117]

Mokdad等[74,118]研究发现,2.0%CNT/2024Al (质量分数)复合材料挤压棒材经挤压加工后,基体合金与复合材料均主要表现为Cu织构{112}<111>和Goss织构{110}<001>,且复合材料的织构强度高于基体合金。进一步在200~400 ℃和应变速率0.001~0.1 s-1范围内对挤压棒材的热压缩变形行为进行了研究,发现复合材料在低温高应变速率条件下发生失稳,而在高温低应变速率下的加工性能最优,对应的微观组织演化机制为动态再结晶。随温度升高再结晶比例增大,棒材的挤压织构变弱。添加CNT使材料的可加工性变差。

增强相尺寸、形状等差异是影响DRA复合材料可加工性的重要因素,而变形工艺则决定了增强相的分布、取向等组织特征。因此,DRA复合材料变形加工核心在于如何控制缺陷、增强相分布、取向和基体晶粒等组织特征。由于DRA复合材料种类繁多,因而完善DRA复合材料变形加工研究,形成系统的数据资料,有利于形成通用性的DRA复合材料成形加工技术。如果能形成不同DRA复合材料的本构方程、加工图与特征组织数据库,并与计算模拟方法相结合,可望提升研究成果的普适性与可靠性,从而加快零件成形加工周期,避免繁琐的工艺摸索带来的不利影响。

4 总结与展望

以DRA复合材料为代表的高性能金属基复合材料,是国家重大需求与国民经济建设需求的战略关键材料,但是其难以塑性成形加工的特点约束了其大规模批量化生产及应用。对金属基复合材料热变形行为研究的最终目的,是掌握其热变形机制特征,为实际生产中热加工参数的制定提供理论依据,从而避免缺陷形成并实现组织控制。本构方程基于经典动力学方法,为DRA复合材料的流变行为与变形条件相关性提供了数学经验公式,尽管难以预测DRA复合材料复杂的变形机制和组织演化,但初步揭示了DRA复合材料与铝合金在变形行为方面的差异。另外,本构方程建立了流变应力与变形条件的数学关系,是开展DRA复合材料零件成形加工仿真模拟的基本工具。

相比本构方程,加工图方法可以更直观地分析金属基复合材料的变形机制,还可以预测导致缺陷形成的流变失稳现象。但由于DRA复合材料的组织和变形的不均匀性,加工图的预测精度仍有待提高。通过结合应变速率敏感指数和温度敏感指数作为辅助分析参数,可以对加工图的分析结果提供必要的补充修正作用,以提高其准确性。相当数量的加工图研究报道,为DRA复合材料的热加工工艺参数制定提供了非常有意义的指导作用。

现有的研究揭示了增强相对DRA复合材料变形组织和缺陷形成的关键影响作用,也发现了变形工艺条件对增强相分布、取向以及晶粒尺寸等组织特征参量的影响。然而,DRA复合材料是一种可设计性极强的材料,基体合金成分、增强相尺寸、形态、种类等诸多因素不仅是DRA复合材料服役性能设计的变量,也对成形加工性能造成显著影响。随着DRA复合材料的不断发展,其变形加工研究从未中断过。但这些研究只提供了个例和片面的结果。未来如果能够建立起DRA复合材料变形加工数据库,并发展出变形加工仿真模拟方法,则有望对DRA复合材料的变形组织实现仿真模拟,从而极大地加快零件成形工艺研发。因此,未来DRA复合材料的热变形研究应加大力度进行研究数据总结和数据库建立,同时开展仿真加工技术研究,以突破DRA复合材料难加工、组织难控制的技术瓶颈,为DRA复合材料推广应用奠定基础。

来源--金属学报