分享：一类介于晶体与准晶体之间的有序结构

秦高梧, 谢红波, 潘虎成, 任玉平

东北大学材料科学与工程学院材料各向异性与织构教育部重点实验室 沈阳 110819

摘要

关键词： 晶体 ; 准晶 ; 近似相 ; Laves相 ; 畴结构 ; 有序结构

根据原子排列的有序性以及旋转对称性的差异,固态物质可以简单地分为3类,即非晶、准晶与晶体。图1所示为自然界中固态物质的占比示意图。非晶体是长程无序结构,原子排列不存在确切的旋转对称,如玻璃、非晶合金和无定型碳等[1]。晶体具有长程有序的原子排列,其结构模型可以简单地通过单个原子或原子簇重复来描述。正因如此,晶体的旋转对称性是严格受限的：即允许2次、3次、4次和6次旋转对称,但是5次、7次以及7次以上的旋转对称都是禁止的[2]。准晶具有长程有序结构,但没有晶格周期性(即不存在平移周期性),其原子排列具有旋转对称性,但都不是传统晶体允许的2次、3次、4次和6次旋转对称。如三维二十面体准晶(5次对称)[2,3,4,5,6,7,8]、二维八边形准晶(8次对称)[9,10]、二维十边形准晶(10次对称)[11,12,13,14]、二维十二边形准晶(12次对称)[15,16,17]等等。

图1   自然界中固态物质占比示意图

Fig.1   Schematic of the solid matters in nature, including the amorphous (red), crystals (blue), quasicrystals (yellow), approximants (baby blue) and ordered structures between the crystals and quasicrystals (green)

自1984年发现准晶以后,人们还提出了准晶近似相的概念,准晶近似相是指短程范围内具有准晶非周期性对称的特征,但长程范围内却具有晶体相的特征(短程非周期性对称结构单元长程范围内具有平移对称性),是一种复杂结构的晶体相[14,18~20]。此外,人们还在快速冷凝合金以及高温合金中发现了一些介于晶体与准晶之间的中间态金属相[21,22,23],这些中间相也表现出与准晶相似的5次(或10次)对称的电子衍射,高分辨原子像显示这些中间态金属相可能是由Frank-Kasper二十面体原子柱组成的具有伪5次对称的微畴结构。目前,搜寻并确认传统晶体与准晶之间是否存在另外的凝聚态结构仍然是一个巨大的挑战。本文综述了固态物质(包括非晶体、晶体、晶体近似相、准晶体以及介于晶体与准晶体之间的有序结构)的研究历程,并着重介绍了作者课题组近期在凝聚态结构物质上的2项新发现,即确认了2种介于晶体与准晶相之间的凝聚态结构,它们在法平面内不具有任何平移周期性,但法平面原子层在法线方向上呈周期性排列,是一类既不属于晶体相,也不同于任何已发现的准晶体的二维有序结构[24,25]。

1 固态物质的结构

1.1 非晶态物质

非晶态物质,通常也被称为无定形或玻璃态物质(amorphous or glassy materials),它是与气态、液态与固态相并立的第4种常规物质状态[1]。而玻璃是最典型、最常见的非晶固体,以至于人们习惯用玻璃来代替非晶固体。然而非晶态物质绝不仅仅局限于玻璃,它包含许多种类,既包括自然界中天然的非晶态固体物质如火山灰、琥珀、树脂、松香、矿物、胶脂、沥青、生物体(软物质),也包括人工合成的氧化物玻璃、塑料、非晶态半导体以及新近迅速发展的非晶态电解质、非晶态离子导体、非晶态超导体和非晶态合金(金属玻璃)等新型非晶态物质。此外,人类的许多食物其实也是非晶态物质,生物体如动物和植物大多也是由非晶态物质所组成,宇宙中大部分水也是以非晶态的形式存在[1]。就整体凝聚态物质而言,相比于种类繁多的非晶态物质,晶体物质只不过是总体凝聚态物质中的特例。如图1自然界中固态物质的占比示意图所示,它表明自然界中大多数固体物质都是非晶态的。

非晶态物质是复杂的多体相互作用体系,其基本特征是原子和电子结构复杂,体系在能量上处于亚稳状态,具有复杂的多重弛豫行为。非晶结构是长程无序的,它没有晶体结构的长程周期性。图2给出了非晶合金[1]和晶态金属的高分辨透射电镜(HRTEM)像对比。可以看到,非晶合金的无序原子结构(图2a[1])和普通金属中的原子晶格像(图2b)完全不同,晶体具有整齐的原子排列,而非晶合金的原子像则很混乱。相应的选区电子衍射花样也完全不同,非晶结构的电子衍射图是较宽的晕和弥散的圆环(图2a插图[1]),而晶体结构则呈现为典型的明亮斑点(图2b插图)。

图2   非晶合金[1]和晶态金属HRTEM像及其相应的选区电子衍射谱对比

Fig.2   Comparison of the HRTEM images and the corresponding selected-area electron diffraction (SAED) patterns of amorphous alloy (a)[1] and crystal alloy (b)

1.2 晶体

晶体是一类具有长程有序原子排列的固态物质,其结构模型可以简单地通过单个原子或原子簇重复来描述(图2b)。人类对晶体的研究源于300多年前,从晶体形态学到晶体结构,形成了一套完善的理论和方法。

17世纪以前,人们对晶体有所认识,但直至17世纪中叶,晶体学才作为一门学科出现[26,27,28]。1669年,丹麦科学家斯丹诺(N. Steno,1638~1686年)首先发现石英和赤铁矿晶体的面角守恒定律(Steno定律),奠定了晶体学的基础。1749年,俄国科学家罗蒙诺索夫(M. Lomonosov,1711~1765年)通过对硝石晶体的研究,确切地论述了硝石晶体角度不变定律并创立了物质结构微分子学说,从理论上阐明了面角守恒定律的实质。1772年,法国学者罗姆·埃·得利(R. Del’lele,1736~1790年)统计了近500种矿物晶体的形态结构,肯定了面角守恒定律的普遍性。1784年,法国学者阿羽伊(R. J. Hauy,1743~1822年)在晶体内部构造方面提出晶体应该都是由无数具有多面体形状的分子平行堆砌而成的,并于1801年发表了揭示晶体外形与其内部构造之间的关系的整数定律(Hauy定律)。

德国科学家魏斯(C. S. Weiss,1780~1856年)以实验的方法测定晶体中的不同旋转轴,并总结出晶体的对称定律,即晶体只可能有1次、2次、3次、4次和6次旋转对称,而不存在5次和高于6次以上的旋转对称。并于1813年首次提出可将晶体分为6大晶系,提出了晶体学中又一重要定律——晶带定律(Weiss定律)。此外,Weiss于1818年和米勒尔(W. H. Miler,1801~1880年)于1839年先后创立了用以表示晶面空间位置的Weiss符号和Miler符号。晶体的左右对称性也是这一时期在石英晶体上首次发现。1830年,德国矿物学家赫塞尔(J. F. C. Hessel,1796~1872年)首先推出了32种晶体对称模型(点群)。诺意曼于1833年首次用基本正确的公式表达出晶面位置的几何对称性的联系,认识到对称性是由内部因素决定的。到了1867年,俄国学者加多林(Axel V. Gadolin,1828~1892年)独自用严密的数学方法推导出晶体外形(有限图形)对称所可能具有的32种对称性。以德国数学家圣佛里斯(S. Floris,1835~1928年)创立的对称型符号及格尔曼和摩根创立的国际符号为标志,完成了对晶体宏观对称理论的总结。到了19世纪末,晶体宏观对称理论迅速发展,整个几何结晶学理论近乎完善。

从19世纪末到20世纪70年代,随着X射线的发现以及广泛使用,晶体形态学发展到晶体结构学,微观对称理论达到日益成熟的境地[26,27,28]。

19世纪中叶,几何学、解析几何学、群论以及物理学的迅速发展,进一步促进了晶体构造理论的完善。19世纪产生的空间点阵和空间格子构造理论在阿羽伊晶体构造理论的启示下逐渐演变为质点在空间规则排列的微观对称学说。法国晶体学家布拉维(A. Bravais,1811~1863年)于1855年运用严格的数学方法修正了1842年德国学者弗兰肯汉姆(M. L. Frankenheim,1800~1869年)推导的15种空间格子假说,并推导出晶体的空间格子有且仅有14种(布拉维空间格子),提出了重合调动理论,奠定了近代晶体构造学理论基础。

但是,重合调动理论只适用于各晶系中对称性高的晶类的对称,对于对称性低的晶类并不适用。在此基础上,德国学者桑克(L. Sohncke,1842~1897年)进一步完善了晶体结构的几何理论,他于1879年引出了微观对称群的概念,推导出包括平移和旋转动作在内的65个桑克点系,用于解释晶系中对称较低晶类的对称问题,但仍具有一定的局限性。俄国结晶矿物学家费多洛夫(E. S. Fedorov,1853~1919年)创立了平行六面体学说,提出反映及反映滑移等新的对称变换,并推导出230种空间群(Fedorov群),圆满地解决了晶体构造的几何理论。此后,德国学者圣佛利斯(A. M. Schoenflies)和英国学者巴罗(W. Barlow)用另外的方法也分别于1891年及1894年推导出相同的230个空间群。至此,晶体构造的微观对称几何理论就这样近乎完善。

19世纪末,晶体构造的几何理论业已成熟,被许多学者所接受。然而,该理论还有待于实验证明。1895年,德国物理学家伦琴(W. K. Rontgen,1845~1923年)意外发现了X射线。1909年,德国学者劳厄(M. Von Laue,1879~1960年)提出了X射线通过晶体会出现干涉现象的猜想,并很快由他的学生弗利德利希和克尼平以实验的方式证明了这一猜想的真实性。此后,法国学者布拉格父子(W. H. Bragg和W. L. Bragg)发表了第一个晶体结构(NaCl晶体结构),并通过对大量晶体结构的测量改善了晶体结构测定的理论和实验技术,开拓了晶体结构研究的新领域。自1909年X射线通过晶体产生衍射效应获得成功以来,目前所有已知晶体结构的测定基本上都是应用上述方法取得。X射线衍射(XRD)分析使晶体结构和分子构型的测定从推断转为测量,这一进展对整个科学的发展有着重要意义。

除了可用XRD方法测定晶体的结构外,透射电子显微镜(TEM)也是研究晶体结构的重要手段。TEM的出现和使用已有90多年历史。在早期,TEM的放大功能可用于观察一些微细晶体的形态。1936年,Boesrch将晶体的电子衍射图像装置安置在TEM中,人们运用选区电子衍射(SAED)谱来研究晶体的微细结构。到了20世纪60年代,高分辨成像理论促进了HRTEM的发展。至今,球差校正的透射电子显微镜(Cs-TEM)点分辨率已优于0.08 nm,人们可以直接观察晶体中的原子像。

TEM开创了固态物质中准周期、非周期性结构研究的新历程。

1.3 准晶

随着透射电子显微镜的应用与发展,运用透射电镜发现准晶是科学历史必然事件。晶体对称理论建立2个多世纪以来,5次及6次以上的旋转对称在晶体学中是禁止的,因为5次及6次以上的旋转对称使得晶体不再具有平移周期性。然而,当以色列科学家舍特曼(D. Shechtman)于1984年在《Physical Review Letters》期刊发表题为“Metallic Phase with Long-Range Orientational Order and No Translational Symmetry”的5次准晶的文章后,立刻引起了整个科学界的震动[3]。5次准晶的发现与提出使传统经典对称理论受到了猛烈冲击。它的发现与C60 “巴基球”[29]及高温超导现象[30]一起并列为20世纪80年代凝聚态科学领域的三大突破。现代准晶科学也从此开始,并很快发展成为一门独立的分支学科——准晶学。

准晶具有准周期性的原子排列,然而它却不能像周期性晶体结构那样简单地用一个原子或原子簇来重复其晶体学特征。自从Shechtman发现准晶以来,目前已有超过200多种准晶体被发现。按准晶在三维空间里的准周期性差异,这些准晶体可以简单地分为3类,即三维准晶、二维准晶和一维准晶。

三维准晶即二十面体准晶,它是已发现最多的一类准晶。二十面体准晶的原子排列在三维空间里都是准周期性的,具有3类旋转对称轴,即5次轴、3次轴和2次轴。图3a是一个典型的Mg-Al-Zn二十面体准晶的5次对称轴电子衍射谱,不同于非晶的衍射环,准晶衍射图谱与晶体类似,具有明锐的衍射斑点,然而它又不是晶体所允许的2次、3次、4次和6次旋转对称。图3b是Mg-Al-Zn二十面体准晶的高分辨高角环形暗场像-扫描透射电镜(HAADF-STEM)像,电子束沿5次对称轴入射,准周期性的原子排列清晰可见。图3c和d[31]展示了一个Cd-Yb 二元二十面体准晶的模拟原子排列及其相应的三维视图,可见二十面体最小团簇单元在三维空间里准周期性排列的细节。

图3   典型Mg-Al-Zn三维二十面体准晶的电子衍射谱、Mg-Al-Zn二十面体准晶的高分辨HAADF-STEM像、Cd-Yb二十面体准晶原子排列模型及Cd-Yb二十面体准晶的三维原子模型(图3a~c电子束沿5次对称轴入射)[31]

Fig.3   Typical electron diffraction pattern of a Mg-Al-Zn three-dimensional icosahedral quasicrystal (a), high-resolution HAADF-STEM image of the Mg-Al-Zn icosahedral quasicrystal (b), modeled atomic arrangement of the Cd-Yb icosahedral quasicrystal (c)[31] and the 3D view of Cd-Yb icosahedral quasicrystal (d)[31] (The electron beam is parallel to the five-fold axis in Figs.3a~c)

二维准晶最显著的特征是原子在法平面内呈准周期性排列,但准周期性的法平面原子层沿法线方向是具有周期性的。目前,已发现的二维准晶主要包括八边形准晶(8次)[9,10]、十边形准晶(10次)[11~14,32]和十二边形准晶(12次)[15,16,17]。其中,以二维10次准晶最为常见。图4[32]展示了二维10次准晶的一些晶体学特征[32],如图4a[32],十边形准晶可用一个正十边形的棱柱体来表示,其中平行于正十边形棱柱体法线方向为10次轴,可以看到,沿着这个方向获得的选区电子衍射谱即为10次轴衍射,衍射斑具有10次旋转对称,是准周期性的,而垂直于正十边形棱柱体法线方向为2次轴,电子衍射斑具有晶体结构衍射特征,说明原子层沿法线方向周期性排列。图4b[32]是一个Al70Mn17Pd13二维十边形准晶的高分辨HAADF-STEM像,电子束沿10次轴入射,与二十面体准晶类似,准周期性的原子排列清晰可见。

图4   二维十边形准晶示意图(可由一个正十边形棱柱体表示,包含平行和垂直于正十边形棱柱体法线方向上的10次和2次轴电子衍射谱)及Al70Mn17Pd13二维十边形准晶的高分辨HAADF-STEM像(电子束沿10次轴方向入射)[32]

Fig.4   Decagonal structure is a 2-dimensional quasicrystal, whose characteristic is well represented by a regular decagonal prism, as schematically shown with the relevant electron diffraction patterns of tenfold and twofold symmetries (a) and atomic-scale HAADF-STEM image of a 2D Al70Mn17Pd13 decagonal quasicrystal, the electron beam is parallel to ten-fold axis (b)[32]

一维准晶,顾名思义,即原子排列只在一个方向上呈准周期性,它是周期性的二维原子层沿其法线方向准周期性堆垛[33]。

此外,从热力学的角度还可以将准晶分为稳定准晶和亚稳准晶。目前,只在三维二十面体准晶和二维十边形准晶中发现了稳定准晶的存在。

1.4 近似相

近似相与准晶具有相同或相似的局部结构,这种局部结构单元准周期性地排列起来便构成了准晶,但是,如果这些局部结构单元周期性地排列在一起便可形成具有平移对称性的晶体结构。由于这类复杂结构既有准晶的特征,也有晶体的特征,晶体学上定义这类结构为准晶近似相或晶体近似相[14,18~20,34]。

目前,已发现的准晶近似相多与二维十边形准晶有关,如单斜的Al13Co4结构、正交的Al-TM (TM,过渡族金属)、Ga-TM晶体相以及六角晶体相等[19]。图5a[34]是Al-Cr-Fe-Si合金沿[010]方向拍摄的高分辨HAADF-STEM像,可以看到准周期性的结构单元(原子像见图5a[34]插图)周期性地排列在一起,便构成了一个单斜的(3/2, 2/1)准晶近似相,图5b[34]是相应的拼砌模型示意图。

图5   利用HAADF-STEM技术沿[010]方向观察到的Al-Cr-Fe-Si合金中的单斜(3/2, 2/1)准晶近似相及其相应的拼砌模型示意图[34]

Fig.5   The [010] HAADF-STEM image of the (3/2, 2/1) orthorhombic approximants, where the same color means the same orientation (a), and the corresponding schematic of the tiles (b)[34]. One shield-like tile (SLT) is highlighted in semitransparent yellow in the upper right area and one enlarged experimental SLT at atomic resolution is inserted in the lower right corner. One SLT consists of two shutter-like hexagons and one pentagon-like star, with the mirror symmetry (m) going through the center from head to tail (a and c represent the lattice parameters of the orthorhombic approximants)

1.5 介于晶体与准晶体之间的有序结构

几乎与准晶发现的同时期,我国科学家郭可信院士和叶恒强院士等在一些合金体系如V-Ni-Si中也发现了一些其衍射存在5次或10次旋转对称的合金相(图6a[23]),然而HRTEM像却显示这些特殊结构既不是晶体相也不是三维二十面体或二维十边形准晶,而是由一些C相、Laves相等Frank-Kasper相组成的微畴结构(图6b[23])。他们把这一类微畴结构定义为介于晶体和准晶体之间的中间结构[21,22,23]。

图6   V-Ni-Si微畴结构的选区电子衍射谱(显示其具有10次对称)及V-Ni-Si微畴结构的HRTEM像(图中每个亮点代表一个二十面体链,显示这个微畴结构是由C相、C14 Laves相等Frank-Kasper相构成的)[23]

Fig.6   SAED pattern taken from a V-Ni-Si microdomain structure showing a tenfold symmetry (a) and HRTEM image of the V-Ni-Si domain structure in which some unit cells of the Frank-Kasper phases, C and L (C14 Laves), are indicated. Each bright dot represents the projection of a chain of interlocked icosahedra (b)[23]

目前,介于晶体和准晶体之间的物质结构报道较少,其定义也比较模糊,搜寻并确认传统晶体与准晶之间是否存在另外一些凝聚态结构仍然是一个巨大的挑战,这对于认识与理解物质世界是非常有意义的。

2 本课题组在凝聚态物质结构上的新发现

2.1 (Mg, In)2Ca非平移对称Laves相

AB2型Laves相是金属材料里最为常见的一类金属间化合物。截止目前,已发现的二元Laves相超过360多种,而三元Laves相的种类则更多,有900多种[35,36]。但是,从晶体结构上来看,则只有C14、C15和C36 3种Laves结构类型,如图7所示。一直以来,人们认为Laves相都是具有严格的旋转与平移周期性的晶体结构,然而,本课题组最近的研究结果表明,存在一类Laves结构在密堆面上不具有任何平移与旋转对称性,是一类新型的介于晶体与准晶体之间的凝聚态结构。

图7   3种典型的Laves相结构
(a) MgZn2 Laves phase, C14, with a stacking sequence of “…ABAB…”

Fig.7   Modeled atomic arrangement of three kinds of Laves phases viewed along the [0001] (a, c) and [112] (b) directions
(b) MgNi2 Laves phase, C36, with a stacking sequence of “…ABAC…”
(c) MgCu2 Laves phase, C15, with a stacking sequence of “…ABCABC…”

Mg-1.5In-0.5Ca合金200 ℃等温时效24 h后,沿[0001]α方向拍摄的纳米盘片析出相的低倍HAADF-STEM图显示,一个六边形的Laves相如盘子一样躺在(0001)α基面上,其直径约为100 nm,如图8a[24]所示,左上插图为该析出相相应的快速Fourier变换(FFT)图,由于FFT只反映HAADF-STEM图中白色富In原子列的晶体学信息,可以看到富In原子列在(0001)P基面上沿6个特定的取向方向上均匀分布[37,38]。图8b[24]是图8a局部区域的放大图,这些原子尺度的HAADF-STEM结果表明,富In的原子列在(0001)P基面上沿6个方向分散排列,把析出相分割成一个由5种拼砌图案键合起来的无任何平移对称性的晶体结构。这5种拼砌图案可以描述为：(1) 边长为“a”的等边三角形;(2) 边长为“a”的等边六边形;(3) 边长为“a+a+2a+a+a+2a”的窄六边形;(4) 边长为“a+2a+a+2a+a+2a”的非等边六边形;(5) 边长为“a+2a+2a+a+2a+2a”的宽六边形。此外,需要说明的是,这5种拼砌模型沿6个方向分布至多可以表现出3种变体。这5种拼砌图案沿3个特定的方向,在一定的几何约束条件下,按照Penrose无缝拼积规则,随机键合在一起,形成了这个特殊的在(0001)P基面上不具有任何旋转对称的Laves相。

图8   Mg-1.5In-0.5Ca合金200 ℃等温时效24 h后的HAADF-STEM图及相应的FFT图(电子束沿[0001]α方向入射)[24]

Fig.8   HAADF-STEM images of the Mg-1.5In-0.5Ca alloy aged at 200 ℃ for 24 h (The electron beam is parallel to [0001]α)[24]
(a) low-magnification HAADF-STEM image (The inset shows fast Fourier transformation (FFT) image)
(b) atomic-scale HAADF-STEM image

图9a[24]是由等边六边形和宽六边拼彻单元沿6个方向有序排列形成的一个局部旋转对称区域,相应的原子排列模型如图9b[24]所示。可以确定这个析出相事实上是由2种晶胞单元构成的,相应的晶胞原子结构如图9c和d[24]所示。晶胞1 (图9c[24])对应于图9a[24]中的区域1 (红色虚圆框),它由中心的In原子列、中间层的Mg原子列和外层的Ca原子列组成;晶胞2 (图9d[24])则对应于图9a[24]中的区域2 (蓝色虚圆框),其结构与晶胞1完全一样,但是由内而外依次是Mg原子列、In原子列和Ca原子列,即晶胞1和晶胞2的In原子和Mg原子占位完全颠倒。由于中心原子列与中间层原子列的原子比为3∶1,因此晶胞1中心In原子列的亮度要远高于晶胞2中间层In原子列的亮度。这2种晶胞都是六方结构,晶胞参数为a=0.625 nm,c=1.031 nm。

图9   原子尺度的HAADF-STEM像及相应的原子排列模型(电子束沿[0001]α方向入射)[24]

Fig.9   Atomic-scale HAADF-STEM image of the (Mg, In)2Ca Laves phase (a), atomic schematic diagrams of corresponding modeled atomic arrangement (b), modeled unit cell-1 marked with red dash cicle in Fig.9a (c), and modeled unit cell-2 marked with blue dash cicle in Fig.9a (d)[24]

与传统的晶体结构相比,该(Mg, In)2Ca Laves相并不能简单地用一个晶胞单元来描述,而是由2种结构相同但Mg和In原子占位完全不同的晶胞单元随机键合在一起的特殊结构,因此这个(Mg, In)2Ca Laves相在(0001)L基面内不具有任何平移周期性,但是沿(0001)L基面法线上原子层呈现周期性排列。此外,它在(0001)L基面内长程范围内也不具有任何旋转对称性,不仅没有传统晶体所应有的2次、3次、4次和6次旋转对称,也没有已知准晶体所具有的5次、8次、10次或12次等非传统旋转对称,是一种介于晶体与准晶体之间的新型凝聚态有序结构。

2.2 Mg-Zn 5次纳米畴结构

Mg-Zn系合金是最早发现具有时效硬化特征的Mg系合金之一,其时效析出序列为super saturated solid solution (S.S.S.S)→β1' (rod-shaped)→β2' (plate-shaped, MgZn2 Laves phase)→β (equilibrium phase,MgZn)[39,40,41,42,43]。然而,其主要强化相β1'的结构与化学成分一直存在巨大的争议,有认为是垂直于基面的MgZn2 Laves相[44,45],也有认为是一种类似于Mg4Zn7的晶体相[46],更有甚者认为是两者的混合物[47,48]。然而,研究[25]表明β1'相既不是MgZn2 Laves相,也不是Mg4Zn7晶体相,更不是MgZn2和Mg4Zn7的混合物,而是一种介于晶体与准晶体之间的由2种最小结构单元(72°菱形和72°等边六边形)沿5个特定的取向方向拼砌而成的包含C14、C15等短程有序的Laves晶体相和二维5次旋转对称结构的纳米畴结构。

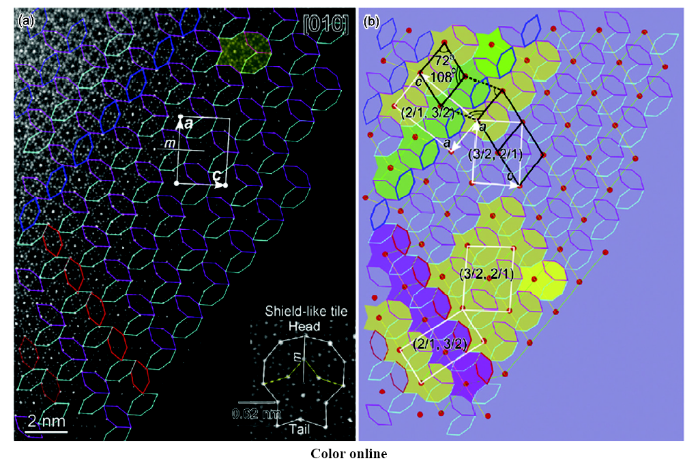
图10a[25]是Mg-2.3Zn合金200 ℃等温时效8 h (峰时效)后的低倍HAADF-STEM像,电子束沿[0001]α方向入射,由图可知,Mg-Zn合金基体晶粒内析出了大量的具有白色衬度的β1'相,这与TEM明场像的观察结果是一致的[25,46~48]。为了进一步揭示这种棒状析出相的晶体结构与原子坐标,使用球差校正的STEM技术进一步表征这些析出相的特征。图10a[25]中被红色虚圆圈出的析出相被进一步放大,原子尺度的HAADF-STEM像及相应的FFT如图10b和c[25]所示。由图可知,析出相内部存在2种衬度的富Zn原子列[37,38],其中衬度较亮的Zn原子列总是位于边长a的顶点处,而衬度较暗的Zn原子列则位于边长a的中间。这些富Zn原子列沿10个特定的取向方向排列,构成2种最小的基本结构单元,即72°菱形结构单元(图10b[25]中标识为R)和72°等边六边形结构单元(图10b[25]中标识为H)。这些不同尺寸的析出相在法平面(001)P上都呈现为类椭圆形,其原子排列在这个二维的法平面上长程范围内也不具有任何平移周期性和旋转对称性。图10d[25]是电子束沿[1120]α方向入射获取的析出相截面图。可以看到,尽管棒状析出相在法平面(001)P上的原子排列不具任何平移周期性,但原子层沿法向量[001]P方向却呈周期性堆垛,具有晶体结构的特征。

图10   Mg-6Zn合金200 ℃等温时效8 h后(峰时效)的HAADF-STEM像 [25]

Fig.10   HAADF-STEM images of the Mg-6Zn alloy after isothermally aged at 200 ℃ for 8 h, viewed along the [0001]α (a~c)[25] and [1120]α (d) directions
(a) low-magnification HAADF-STEM image
(b, c) some precipitate-rods circled in Fig.10a are enlarged and shown, the atomic-scale HAADF-STEM images indicates the structure in the observed 2D containing two separate unit cells, whose lattice images are labeled as H and R, respectively. The inset in Fig.10b is the corresponding FFT image. The unique characteristics of the 2D five-fold nanodomain structure, five orientation rhombi variants bonding together to form a star pattern and five orientation equilateral hexagon variants bonding together to form a petal pattern, are marked by red star and yellow petal, respectively
(d) atomic-scale HAADF-STEM image viewed along [1120]α direction indicates the precipitate-rods with periodic arrangements along the normal vector

图11a[25]是根据原子尺度的HAADF-STEM图绘制的一个沿 $\left[001\right]$P方向观察到的β1'棒状析出相的原子排列模型,为了确定这个析出相的晶体结构与原子占位,我们考虑了原子二十面体团簇[22,23],即每个顶点Zn原子都被周围的12个原子所簇拥,形成一个以Zn原子为中心、周围由12个原子构成的二十面体团簇结构。在图11a[25]的原子结构模型中,Mg原子用蓝色圆球表示,而顶点处Zn原子(对应于HAADF-STEM图中衬度最亮的质点)用红色圆球表示,边长a中点处的Zn原子(对应于HAADF-STEM图中衬度较弱的质点)则用黄色圆球表示,可以看到所有顶点处Zn原子周围都有10个原子,加之这个Zn原子上面和下面各有一个Zn原子,便可形成了一个配位数为12、以这个Zn原子为中心的二十面体团簇模型(二十面体团簇三维视图见图11b[25])。此外,这个棒状析出相中存在6种不同的二十面体团簇结构,如图11b[25]所示,根据键合角的不同,可以分为：(1) 键角为“72°+72°+72°+72°+72°”的二十面体团簇结构,这种情形下5个黄色Zn原子同处一侧,而5个Mg原子则同处另一侧(如图Fig.11b-1);(2) 键角为“72°+108°+72°+108°”的二十面体团簇结构,在这个结构模型中2个黄色Zn原子在左边,另外2个黄色Zn原子在右边(如图Fig.11b-2);(3) 键角为“72°+72°+108°+108°”的二十面体团簇结构,其中3个黄色Zn原子在左边,另外1个黄色Zn原子在右边(如图Fig.11b-3);(4) 键角为“72°+72°+72°+144°”的二十面体团簇结构,在此结构模型中所有的4个黄色Zn原子都在左边(如图Fig.11b-4);(5) 键角为“108°+108°+144°”的二十面体团簇结构,在此结构模型中2个黄色Zn原子在左边,1个黄色Zn原子在右边(如图Fig.11b-5);(6) 键角为“72°+144°+144°”的二十面体团簇结构,所有的3个黄色Zn原子都在左边(如图Fig.11b-6)。由这6种不同的二十面体原子团簇构成的6种二十面体原子柱在(001)P面(法平面)上沿5个特定的取向方向,按照一定的几何约束条件结合在一起,形成了这个特殊的包含2种最小结构单元的棒状析出相[25]。

图11   Mg-Zn合金中析出的5次纳米畴结构的原子示意图 [25]

Fig.11   Atomic schematic diagrams of the precipitate-rod in the Mg-Zn alloy (L—plane distance between Mg atom and adjacent apex Zn atom, Z—the atomic layers)[25]
(a) modeled atomic arrangement of the precipitate-rod, viewed along [001]P direction (five-fold axis)
(b) the six kinds of icosahedral clusters models in the precipitate-rod
(c) modeled atomic structure of the 72° rhombus unit cell
(d) modeled atomic structure of the 72° equilateral hexagon unit cell

图11c和d[25]是72°菱形和72°等边六边形的结构单元原子结构模型,从[100]P和[010]P方向的原子排列可以判断这个棒状析出相沿[001]P (法线方向)具有周期性的“…ABAC…”的堆垛序列。此外,从图11c[25]可以看到72°菱形结构单元内部包含2个Mg原子,一个在B层,另一个在C层,每个Mg原子与最近邻顶点Zn原子(红色Zn原子)的平面距离为0.618a,正好是边长a的黄金分割距离(图11c[25] [001]视图)。因此,72°菱形结构单元的化学成分即可被确定为MgZn2。72°等边六边形结构单元结构较为复杂,如图11d[25]所示,它内部包含6个Mg原子,其中2个在B层,而C层则有4个Mg原子,这样才能确保72°等边六边形顶点6个Zn原子的配位数都为12。如图11d[25] [001]视图所示,这个72°等边六边形可以拆分为2个相互交叉的72°菱形,其内部的6个Mg原子与最近邻顶点Zn原子的平面距离(L)也是0.618a。同理,72°最小等边六边形结构单元的化学成分可被确定为MgZn。

72°菱形和72°等边六边形结构单元在特定的约束条件下,沿5个取向方向随机自组装在一起,最终在一些区域内形成了短程有序的晶体相(图11a[25]中标示的C14、C15结构),在有些区域则形成了具有5次旋转对称的结构,即5个72°菱形结构变体结合在一起的星型结构(图11a[25]绿色星型标识)和5个72°等边六边形结构变体结合在一起的花瓣结构(图11a[25]绿色花瓣标识)。这些按照Penrose几何拼图法则拼砌在一起形成的这个特殊结构在二维的法平面上长程范围内不具有任何平移周期性和旋转对称性,它既不属于晶体相,也不同于任何已发现的三维二十面体准晶或二维十边形准晶,是一个包含有C14、C15等短程有序的Laves晶体结构和5次旋转对称结构的新型二维有序结构——5次对称纳米畴结构。此外,值得一提的是,随着时效时间的增加,这个5次对称纳米畴结构将逐渐转变为MgZn2 Laves相[25,46,48],因此它是一个亚稳析出相。

3 结 论

本文综述了凝聚态物质的结构研究,着重介绍了我们近期利用球差校正的HAADF-STEM技术获得的镁合金析出相的新结构。其中一种是(Mg, In)2Ca “Laves相”,由2个晶胞单元沿6个方向排列,构成5种拼砌图案,这5种拼砌模型按照Penrose几何拼图规则随机键合在一起,在(0001)L基面上长程范围内不具有任何旋转与平移对称性,但是沿(0001)L法线方向上具有周期排列特征。另一种是Mg-Zn合金中的纳米析出棒,沿纳米棒方向原子面呈现周期性排列,但是其原子面是一种由72°菱形结构单元(MgZn2,a=0.454 nm,c=0.522 nm)和72°等边六边形结构单元(MgZn,a=0.454 nm,c=0.522 nm)沿5个方向按照Penrose几何拼图规则自组装而成,原子面内包含C14、C15等短程有序的Laves晶体相和5次旋转对称结构的二维5次纳米畴结构。

这2种物质结构共同的特征是沿一个方向原子面呈周期性排列,而垂直该方向的原子面内原子的堆垛由2个基本单元按照Penrose几何拼图规则连接而成,长程范围内不具有任何平移与旋转周期性。这种凝聚态物质结构既不属于晶体相,也不同于任何已发现的准晶体的二维有序结构或准晶近似相,是一种全新的、介于准晶和晶体之间的凝聚态物质有序结构。

尽管我们在合金体系中发现了这种新的凝聚态物质结构,在无机非金属物质或有机物包括蛋白质中是否存在这种类型的结构,依然是一个非常具有探索性的方向。如何在数学上描述这种结构以便于后续的理论建模及性能预测,也依然是一个具有挑战性的课题。

来源--金属学报