分享：固溶体中的化学结构单元与合金成分设计

董闯1, , 董丹丹2, 王清1

1 大连理工大学三束材料改性教育部重点实验室 大连 1160242 大连大学物理科学与技术学院 大连 116622

摘要

关键词： 化学结构单元 ; 团簇加连接原子模型 ; 固溶体 ; 近程有序 ; 铜基二元工业合金

工业合金多以固溶体结构为主,其发展依赖于长时间的经验探索和冗长的工程实践,每一种工业合金的研发都需要大量的投入,如何简化设计流程是人们一直以来关注的问题。成熟的工业合金具有特殊的成分,这表明一定存在某种类似于分子的结构单元,能够反映工业合金成分的特殊性。长期以来,人们忽视了合金的成分根源这一基础问题,主要原因是缺少合适的原子结构模型来处理这些固溶体合金。需要说明的是,即便是服役组织复杂的工业合金,其高温态往往呈单相,例如各种组织形态的钢均对应于高温单相奥氏体固态,在这个区间可以实施均匀化处理以弥补铸态缺陷,高温母相固溶体的稳定性决定了后续组织演化。因此固溶体的模型化及其稳定性是合金成分设计的普适性基础。

固溶体合金在长程范围上保持着溶剂原子的点阵结构,但溶质原子在合金中的化学分布相对复杂,如何理解溶质原子在溶剂原子点阵中的分布模式以及相关的结构稳定性是建立固溶体结构模型的关键。对固溶体中原子结构的研究最早可追溯到1919年,Tammann[1]提出经过长期退火的合金其原子倾向于分离并且位于规则的位置。Johannson和Linde[2]通过X射线分析方法证实了在Au-Cu合金中确实存在这样的分离。Bradly和Jay[3]在Fe-Al体系中也发现了类似现象。以上实验结果表明合金中的有序程度与温度密切相关。1934年,Bragg和Williams[4,5]提出了利用长程有序参数S来定量描述固溶体合金中的长程有序结构。随后Bethe[6]对Bragg-Williams方法进行改进,提出近程有序参数σ (order of neighbors)来描述在一个给定原子附近找到一个不相同原子和找到一个相同原子可能性的差异。直到1950年,Cowley[7,8,9]提出短程序参数(short-range order parameter) α来描述固溶体合金中的短程有序特征。它给出了二元固溶体合金中,以溶质原子为心,每一层的化学成分与平均成分的偏差。然而,α序参数只揭示了围绕某个溶质的中程范围内化学元素振荡分布的图像,不能给出一个给定固溶体中任何有关化学成分起源的信息,更不能理解具有优异性能的工业合金的成分选取。解决这个基础而实际的问题需要建立固溶体合金近程序结构模型。

本文首先总结本课题组过去十余年发展的团簇加连接原子模型,该方法适用于描述各种合金中的近程有序结构,包括准晶、非晶和固溶体[10]。该模型认为任何一个合金相的近程序结构都可以简化成第一近邻团簇加上若干位于次近邻的连接原子2部分,团簇相互孤立,其间隙由连接原子填充,表示成统一的团簇式形式为：[团簇](连接原子)x,其中x是连接原子的个数。这种团簇式形式的结构单元被称做化学结构单元[11]。通过引入Friedel振荡机制,可解决团簇密堆的中程序堆垛结构以及相应的原子密度计算公式,进而可以定量计算固溶体合金的化学结构单元的成分式。最后,利用该方法计算得到铜基二元体系Cu-(Zn, Ni, Al, Be, Sn)工业合金中的最佳化学结构单元,并且这些成分式与对应体系中最常用的工业合金牌号高度吻合,说明优质合金的特定成分的确源自化学近程序结构单元,从而为理解现有合金成分及进一步合金优化提供了一种全新而有效的方法。

1 固溶体合金的特征化学近程序结构描述：团簇加连接原子模型及化学结构单元

团簇加连接原子模型始于准晶的描述,后来在非晶合金体系得到完善[10],近年来用于合金固溶体[12]。其核心思想为任何结构均可描述为第一近邻团簇加上若干次近邻连接原子的单一结构单元,表述为团簇成分式[第一近邻团簇](连接原子)。以一种常见的非晶合金晶化相Al2NiZr6 (InMg2结构)的结构描述为例,该结构的单胞里含有4种结构占位,以其为心,定义出4种配位多面体团簇,分别为[Ni-Zr9Ni2]、[Al-Zr9Al2]、[Zr1-Ni2Zr8Al2]、[Zr2-Ni1Zr8Al4],这里方括号里面的第一个原子为中心原子,横线后面为第一近邻壳层上的原子,上角标表示非等效的原子占位,下角标表示原子的个数。相应的团簇成分式为[Ni-Zr6]Al、[Al-Zr3]Ni1/2、[Zr1-Ni1/3Zr1Al2/3]、[Zr2-Ni1/3Zr1Al2/3]。注意到,第一种团簇式具有最多的原子个数,显示出该团簇具有最大的孤立度,即团簇特性最为明显,应该具有最高的结构稳定性,实际上,就是该团簇,搭配以3个连接原子,给出该体系最佳非晶形成能力成分点：[Ni-Zr9Ni2]Al2Ni≈Zr60Ni26.7Al13.3[13],说明了相近结构之间存在着某种特定团簇的结构遗传,该团簇被称为该相的主团簇,并认为它构成了对应的非晶态的主体局域团簇[14]。事实上,目前所发现的块体非晶合金成分均满足源自对应进行的某种主团簇加上1个或者3个连接原子,且每个团簇式所含价电子个数e/u恒定为24电子[15],例如Cu-Zr体系中具有最高非晶形成能力的成分点之一Cu64Zr36可完美解析为[Cu-Cu7Zr5]Cu≈Cu64.3Zr35.7,e/u≈23.7[16]。需要指出的是,非晶态中的团簇完全孤立,其间由连接原子填充,因此结构和成分式在团簇加连接原子模型下变得极其简单,正如Macky当年所提出的[17]。

由于上述结构描述方法实际上体现了近程序结构的作用,属于一般性的结构图像,类似的团簇式规律应该同样适用于由化学近程序主导的任何结构。例如Al6Fe准晶的团簇式为[Fe-Fe1Al11]Al≈Al85.7Fe14.3≈Al6Fe,这里的二十面体团簇源自晶化相Al3Fe[18]。下面介绍工业合金的基础结构——固溶体的结构特征以及团簇模型。

合金固溶体以化学近程序为特征,因此早期的固溶体结构模型[19,20]一般基于短程有序或者电子结构。对于前一种情况,溶质原子和溶剂原子根据它们之间的相互作用模式表现出近邻构型,溶质原子在溶剂原子基体点阵中的径向分布可以用序参数来描述。对于后一种情况,忽略单个电子的行为,把合金看成原子和价电子的混合,其稳定机制由Fermi面和Brillouin区相互作用决定[21],认为当Fermi面和Brillouin区相切的时候系统最稳定,即2kF≈Kp (kF为Fermi波矢,Kp为Brillouin区的宽度)。Friedel给出了这种情况下的严格处理方法,提出Friedel振荡描述固溶体结构[22],指出杂质电荷(这里为溶质原子)周围的屏蔽电子会产生极化,从而导致电子密度的振荡分布。这种强烈的电荷屏蔽作用发生在溶质原子的周围,是短程有序形成的根本原因。

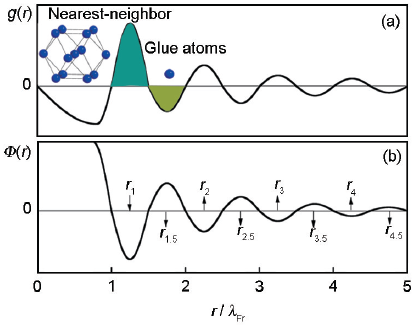
金属中含有大量的传导电子,当一个杂质电荷被引入到电子体系时,杂质电荷周围的电子云会产生极化来屏蔽杂质电荷对体系产生的扰动,导致杂质电荷周围电子云密度的重新分布[23]。杂质周围屏蔽电荷表现出的这种长程振荡就是所谓的Friedel振荡[24]。如图1所示,在液相和金属玻璃中,一个位于r处的电子能够感受到的总势能函数Φ (r)正比于一个正弦函数,Φ (r)∝-sin(2kFr)/r3,势函数形式如图1b所示。电子的这种振荡行为会反过来影响原子密度的分布,引起正空间原子密度的振荡。图1a所示为对分布函数g(r),可以看出原子密度在势函数波谷处取得极大值,即原子倾向于占据势函数波谷的位置。势函数波谷的中点位于rn=(1/4+n)λFr,n=1、2、3、…,其中λFr=π/kF,为Friedel波长。液相和金属玻璃中原子的这种层状分布称为球周期序。这些势函数的波谷区域用rn表示,波峰区域用rn+0.5表示,如图1b所示。势函数第一个波谷的中心位置r1对应于团簇半径r1=(5/4)λFr=1.25λFr。

图1   对分布函数g(r)及Friedel振荡的有效对势函数Φ(r)∝-sin(2kFr)/r3

Fig.1   Pair distribution function g(r), with the location zones of the nearest-neighbor and glue atoms being labeled (a), and the corresponding effective electronic potential Φ(r)∝-sin(2kFr)/r3 arising from Friedel oscillation (b) (rn and rn+0.5 mark respectively the central positions of the negative and positive potential zones; the radial distance r is scaled with Friedel wavelength λFr)

依据团簇加连接原子模型,对上述结构图像做如下简化：

(1) 中程范围上的振荡可以被简化为一个最小的区域,在这个区域内,电荷的扰动接近中性,对应于最近邻的团簇部分加上位于团簇外层的连接原子部分,从而定义出固溶体中的类似于分子的化学结构单元。

金属中电子的这种不完全屏蔽行为表明由中心杂质(溶质原子)产生的电荷振荡不能被最近邻原子完全屏蔽(与分子中第一近邻形成完全电中性对比)。因此,在势函数中一个深的波谷区域r1外,总会伴随着一个波峰区域r1.5,随后又会有一个波谷区域r2。只有到了一定的中程距离之后,振荡完全衰减,体系呈现电中性。由于势函数以距离的三次方形式迅速衰减,其中第一个波谷和第一个波峰的振荡相对最强烈。由此,依据本课题组前期发展起来的团簇加连接原子模型[10],定义一个类似于分子的化学结构单元(chemical unit),涵盖位于r1的最近邻团簇部分加上位于r1.5的连接原子部分,这是近程序结构的最极致的简化,如图1a中阴影部分所示。在理想满足原子间相互作用情形下,这种简化在r1和 r1.5区内接近于电中性,杂质电荷的影响在第一个振荡周期内基本得到完全屏蔽。这就是高稳定性合金必然具有简单团簇成分式的根本原因,即化学结构单元就是描述理想近程序结构的团簇式。化学结构单元就是合金中的“分子”,兼具结构、成分和电子结构信息,其成分由类似于分子式的团簇式描述。

对于稀固溶体,由于溶质的含量非常少,2个溶质所在的团簇式相距非常地远,溶质间的相互作用几乎可以忽略。对于浓固溶体,也就是本工作所讨论的系统,溶质含量较高,溶质所在的团簇式之间存在关联,需要明确团簇式之间的堆垛模式,建立完整的结构模型。

(2) 结合中程范围的球周期性,建立团簇共振模型,给出化学结构单元之间的堆垛方式,最近邻团簇位于势函数第三个波谷的位置r3=(13/4)λFr=2.6r1。

近邻原子之间形成团簇是原子层面上的近程有序,而在中程序上团簇和团簇之间还存在着一定的有序性,可以视为球周期性的延伸,表现为相邻的团簇倾向位于势函数第三个波谷处r3的位置[15]。团簇的半径为r1=1.25λFr,在没有团簇搭接的情况下(即团簇保持完全的孤立性,类似于非晶态中主团簇的分布行为),2个相邻团簇之间的距离为2.5λFr。如果相邻团簇位于势函数第二个波谷r2区域(2~2.5λFr),近邻团簇与中心团簇之间将会产生搭接,从而破坏化学结构单元的完整性。因此,近邻团簇倾向位于势函数的第三个波谷r3区域(3~3.5λFr)。以fcc纯金属结构为例说明化学结构单元的堆垛方式。fcc结构中的团簇为CN12 (coordination number)的立方八面体团簇[25],中心原子到最邻原子的距离,也就是团簇半径为r1=<1/2, 1/2, 0>a= $\begin{array}{c}?/\sqrt[]{2}\end{array}$,其中a为晶格常数。团簇半径与Friedel波长之间存在关系r1=(5/4)λFr=1.25λFr,得到晶格常数a与Friedel波长λFr之间的关系为a= $\begin{array}{c}1.25\sqrt[]{2}\end{array}$λFr。在fcc结构中有3个团簇间距的矢量位于r3区域内,分别是<1, 1, 1>a = $\begin{array}{c}?\sqrt[]{3}\end{array}$≈3.06λFr、<3/2, 1, 1/2>a≈3.31λFr和<2, 0, 0>a≈3.54λFr。其中<3/2, 1, 1/2>晶向上的团簇最接近理想的球周期堆垛方式,如图2所示,这个团簇间距与理想球周期序对应的团簇间距r3=2.6r1非常接近。

由于固溶体中团簇式的定义以及分布与非晶态中主团簇的完全一致,因此,固溶体可以视为化学非晶态(chemical amorphous state),即在给定的基础点阵架构上,溶质元素以类似于非晶态的团簇形式散布于溶剂的基体上。

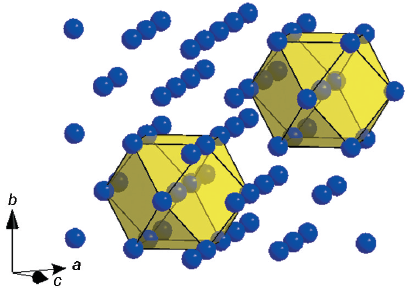
图2   fcc结构中最理想的球周期堆垛方式

Fig.2   Ideal spherical-periodicity packing of clusters in fcc structure, where neighboring cuboctahedral clusters are located at <3/2, 1, 1/2>a position with the distance of r3=2.6r1, a being the lattice constant of the base fcc lattice

2 化学结构单元的计算

在上节建立了一个完整的结构模型,包括描述近程序的化学结构单元以及结构单元在中程序上的堆垛。明确结构单元在中程上的堆垛方式可以计算出浓固溶体中单位化学结构单元中包含的总原子个数,实现连接原子个数的准确定义。

建立了固溶体结构的结构模型之后,利用该模型可计算高溶质含量的置换型固溶体中的化学结构单元,这些固溶体满足单一化学结构单元,并且团簇之间满足球周期排列,相邻团簇位于r3区域。

首先计算固溶体的平均原子密度。假设团簇加连接原子模型的局域有序和团簇堆垛的中程球周期序在近熔点状态的液体和其对应的初级固溶体中保持不变。这个短程序结构遗传性是一个合理的假设,例如,中子衍射实验[26]表明,液态Fe接近熔点时的近程序与高温结构δ-Fe中的近程序非常相似;液态Al在熔点附近的X射线衍射实验[27]表明,其结构因子与对应晶态中的接近。

非晶合金的团簇共振模型[15]指出,具有高形成能力的理想金属玻璃(这里称为高液态稳定性),其团簇之间的堆垛满足球周期序,相邻团簇位于Friedel振荡势函数的第三个最小值处,r3=2.6r1。假设团簇是由硬球堆垛而成,连接原子位于团簇的间隙,平均原子密度ρa可以通过计算r3为半径的体积内所包含原子的个数来确定,并且ρa与团簇式内含有的原子个数Z有关：ρa=[13.33×(13/32)+1]×Z/(r33×4π/3)。因此一个化学结构单元中含有的总原子个数Z可以表示为：

$\begin{array}{c}?=?{?}_{?}{?}_1^3\end{array}$(1)

式中,c为常数。当最近邻团簇恰好位于势函数第三个波谷的中点r3=2.6r1时,此时团簇排布满足理想共振态,c=(4π/3)×2.63/(13.33×13/32+1)≈11.476。对于非理想排布的团簇,近邻团簇位于r3的区域内,这个区域的边界为2.4r1和2.8r1,此时常数c的下限和上限分别为9.026和14.333。

对于纯金属可以直接算出Z值,因为ρar13为常数。例如,对于fcc结构金属,ρa=4/a3 (每个单胞中有4个原子,a为晶格常数),团簇半径为r1= $\begin{array}{c}?/\sqrt[]{2}\end{array}$(2个相邻原子沿面对角线的距离),由此得到ρar13= $\begin{array}{c}\sqrt[]{2}\end{array}$,Zfcc=16.2。因此,对于纯fcc结构金属,最接近整数情况的化学结构单元形式为[M-M12]M3,即CN12立方八面体团簇加上3个连接原子。

对于固溶体合金来讲,平均原子密度ρa和团簇半径r1都取决于溶质原子在团簇式中的位置,而这个位置取决于溶质原子与溶剂原子相互作用的模式：

(1) 相互吸引。这种情况通常发生在2种原子混合焓ΔH为负值的时候,即ΔH<0 (ΔH表示合金体系中异类原子成键与同类原子成键时系统势能的差异。ΔH<0,表示异类原子成键时势能更低,系统更稳定;ΔH>0,表示系统倾向于同类原子成键)。溶质原子倾向于位于团簇的中心,这样才能与周围的溶剂原子产生最大的相互作用,形成溶质原子为中心、溶剂原子为壳层的团簇结构。当溶质原子的含量过多时,多余的溶质将占据连接原子的位置。例如,fcc结构的Cu-Zn固溶体,2种原子的ΔH<0[28],且溶质Zn原子的含量过多,理想的团簇部分为[Zn-Cu12],连接原子部分为Cu和Zn的混合。

(2) 相互排斥。这种情况通常发生在ΔH>0的时候。溶剂原子倾向于与溶质原子分离,团簇部分由溶剂原子构成,溶质原子则更倾向于占据连接原子的位置。例如,对于fcc结构Cu-Ni固溶体,混合焓为正值ΔH=+2 kJ/mol[29],理想的团簇部分为[Cu-Cu12],连接原子为Cu和Ni的混合。

(3) 中性作用。这种合金系统中的溶质原子与溶剂原子的性质非常接近,因此溶质原子可以形成近乎随机分布的模式。尽管在真实的合金中很少有这样的例子,这种类型的固溶体可以被看作由平均原子构成,因此化学结构单元与纯金属中的情况一致,例如对于fcc结构,其形式为[M-M12]M3。

对于fcc结构固溶体,溶剂原子B构成单层的立方八面体团簇,团簇半径r1=2RB,RB为溶剂原子B的半径;当溶质原子A占据团簇中心时,团簇半径变为r1=RA+RB,RA为溶质原子A的半径。

平均原子密度ρa定义为单位体积内包含的原子的个数,是平均原子体积Va的倒数。Va根据所有溶质原子和溶剂原子的原子体积分数之和计算获得：1/ρa=Va=ΣfiVi,fi和Vi分别为元素i的原子分数和原子体积。这个计算是建立在2种元素混合时原子体积保持不变的基础上。对于fcc结构固溶体,Vi=(4π/3)Ri3/0.74,0.74为fcc结构的密堆率,Ri为元素i的原子半径。

因此对于任意fcc结构的浓固溶体系统A-B,A为溶质原子,B为溶剂原子,理想的化学结构单元可以表示为[A-B12]AxBy或[B-B12]AxBy。对于第一种情况,式(1)变为：

$\begin{array}{c}?=??({?}_{?}+{?}_{?}{)}^3/[\frac{1+?}{13+?+?}?(\frac{4}{3}??{?}_{?}^3/0.74)+\end{array}\begin{array}{c}\frac{12+?}{13+?+?}?(\frac{4}{3}??{?}_{?}^3/0.74)]\mathit{}\end{array}$(2)

由Z=13+x+y,(x, y)的关系可以表示为：

$\begin{array}{c}??{?}_{\raisebox{1ex}{$?$}\!\left/ \!\raisebox{-1ex}{$?$}\right.}^3+?=2.03?({?}_{\raisebox{1ex}{$?$}\!\left/ \!\raisebox{-1ex}{$?$}\right.}{+1)}^3-{?}_{\raisebox{1ex}{$?$}\!\left/ \!\raisebox{-1ex}{$?$}\right.}^3-12\end{array}$(3)

式中,RA/B为溶质原子和溶剂原子的半径比。

对于第二种情况,溶质原子只占据连接原子位置,公式(1)中的团簇半径r1等于2RB,[B-B12]AxBy中的(x, y)表达式为：

$\begin{array}{c}??{?}_{?/?}^3+?=3.22\end{array}$(4)

对于式(3)和(4),最接近整数解的(x, y),只与溶质原子相对溶剂原子的半径比RA/B有关。

3 典型铜基二元工业合金的化学结构单元

本节利用固溶体结构模型分析fcc结构典型铜基二元工业合金中的化学结构单元,包括Cu-Zn、Cu-Ni、Cu-Al、Cu-Be和Cu-Sn,这些体系的相图中有相对较宽的固溶区间,并且溶质的浓度较高,能够用单一的化学结构单元来描述。解析后的化学结构单元列于表1。

3.1 Cu-Zn

在高温下,fcc结构的铜基体中可以固溶39% (质量分数,下同)的Zn[30]。根据ASM手册[31],α黄铜具有较宽的的成分区间,从Zn含量最低的合金牌号C21000 (95Cu-5Zn)一直到Zn含量最高的Muntz合金C28000 (60Cu-40Zn)。在这些牌号之中,弹壳合金C26000 (70Cu-30Zn)的应用最为广泛。

很早以前就有人仔细测量过α黄铜单晶样品中的Cowley短程序参数α[32]。以溶质原子Zn为中心,最近邻壳层的α值为α110=-0.1373,负值表明第一近邻倾向于异类原子Zn-Cu近邻,下一壳层的α值为α200=0.1490,表示该壳层倾向于Zn-Zn近邻,这种分布方式满足Zn-Cu之间负混合焓所预期的情况。根据团簇加连接原子模型,当合金中含有足够的Zn时,化学结构单元可以表示为[Zn-Cu12]ZnxCuy,连接原子是Zn和Cu的混合。这种表达形式与实验结果一致,Zn原子为心,第一近邻为12个Cu原子,表现为Zn-Cu近邻,与第一壳层为负的序参数α110吻合;连接原子中为Zn和Cu的混合并且倾向于Zn原子富集,这样才能表现出Zn-Zn近邻的趋势,与第二壳层为正的序参数α200吻合。根据式(2),化学结构单元中包含的总原子个数Z与Zn和Cu之间的原子半径差异有关。对于金属原子采用十二配位多面体情况下的Goldschmidt半径,RA=RZn=0.139 nm和RB=RCu=0.128 nm[33]。通过计算获得x和y之间的关系式满足1.28x+y=5.12。这个关系式所给出的连接原子中Zn、Cu原子的个数具有多种组合情况,每一种情况对应的化学结构单元都同时满足局域近程序和中程球周期序。

1.28x+y=5.12最接近整数的(x, y)解为(4, 0),即连接原子位置完全被4个Zn原子占据,形成了[Zn-Cu12]Zn4形式的化学结构单元,在这种情况下,最近邻的团簇最接近于中r3的位置,满足理想的球周期分布。[Zn-Cu12]Zn4=70.0Cu-30.0Zn (%),恰好为使用最广泛的弹壳黄铜合金C26000 (70Cu-30Zn)。

3.2 Cu-Ni

Cu-Ni合金由于其优异的抗海水腐蚀能力被广泛应用在管道和船舶材料中。Cu-Ni合金的工业牌号也有着较宽的成分范围,从Ni含量最低的C70400 (95Cu-5Ni)到Ni含量最高的C71500 (70Cu-30Ni)。最常用的牌号为C70600 (90Cu-10Ni)和C71500 (70Cu-30Ni)[31]。

由于Cu-Ni之间的正混合焓ΔHCu-Ni=+2 kJ/mol[29],Ni原子倾向于占据团簇式中连接原子的位置,团簇式形式为[Cu-Cu12]NixCuy。Ni原子的Goldschmidt半径为RA=0.125 nm[33]。根据式(3),得到(x, y)的关系式0.93x+y=3.22。这个关系式没有非常接近整数值的(x, y)解,因此需要考虑所有x+y=3的组合。团簇式形式为[Cu-Cu12](Ni, Cu)3,意味着连接原子占位上的Ni原子和Cu原子倾向于随机分布。这一点可以通过实验结果证实：在Cu80Ni20合金中,第二壳层的短程序参数值非常小,α2=α200=-0.058[34],这个值大约只有Cu-Zn合金的1/3,表示该位置只有轻微富Ni的倾向。考虑到这一点以及x+y=3,最可能的团簇式形式为[Cu-Cu12]Ni2Cu1=88.3Cu-11.7Ni (%),该团簇式解释了最常用的合金牌号C70600 (90Cu-10Ni)。另外2个整数解对应的团簇式形式[Cu-Cu12]Ni1Cu2和[Cu-Cu12]Ni3没有对应的合金牌号,因为不满足连接原子位置上Ni原子只是轻微富集的事实。

3.3 Cu-Al

Cu-Al合金有高强度、高的抗氧化性和耐机械磨损性。典型的Cu-Al二元工业合金只有2个：C60600 (95Cu-5Al)和C60800 (92Cu-8Al)[31]。Al在Cu中的最大固溶度为9.3%[35],因此Cu-Al合金的牌号相对较少。

Cu-Al的混合焓为ΔHCu-Al=-1 kJ/mol[36],Al原子倾向于占据团簇中心的位置,对应的团簇式形式为[Al-Cu12]AlxCuy。Al原子的Goldschmidt半径为RA=0.143 nm[33]。根据式(2),得到(x, y)的关系式1.39x+y=5.85。最接近整数的(x, y)解为(2, 3),对应的团簇式形式为[Al-Cu12]Al2Cu3=92.2Cu-7.8Al (%),很好地解释了合金牌号C60800 (92Cu-8Al)。另一个合金牌号C60600 (95Cu-5Al)可以暂时利用团簇式[Al-Cu12]Al1Cu4=95.0Cu-5.0Al (%)来解析,这时对应的(x, y)解为(1.3, 4),偏离整数解1。这2个合金牌号中,92Cu-8Al的原子在近程上和团簇在中程上的堆垛更接近于理想球周期序。

3.4 Cu-Be

Cu-Be合金具有高强度和高弹性,可以作为好的热电导体,最常用的合金牌号为C17200 (98Cu-2Be)[31]。

Cu-Be之间的混合焓接近于0[36],表明Cu和Be之间的相互作用较弱,相对于之前分析的合金而言,该体系中的溶质原子倾向于随机分布。实验测得的短程序参数为正[37],这表明Cu-Be之间倾向于彼此分离,一般的化学结构单元形式为[Cu-Cu12]BexCuy。Be原子的Goldschmidt半径为RA=0.113 nm[33]。根据式(3),得到(x, y)的关系式为0.69x+y=3.22。最接近整数的(x, y)解为(2, 2),对应的团簇式为[Cu-Cu12]Be2Cu2=98.1Cu-1.9Be (%),恰好对应于最常用的合金牌号C17200 (98Cu-2Be)。Be在Cu中的最大固溶度为2.7%[38],这个成分位于固溶极限内。

3.5 Cu-Sn

锡青铜是一种非常古老的合金,有很多合金牌号,但是最常用的合金牌号为C90800 (88Cu-12Sn)[31]。

Cu-Sn的混合焓ΔHCu-Sn=+7 kJ/mol[36],Sn原子倾向于占据连接原子的位置,一般的团簇式形式可以表示为[Cu-Cu12]SnxCuy。Sn原子的Goldschmidt半径为RA=0.155 nm[33]。根据式(3),得到(x, y)的关系式1.78x+y=3.22。唯一最接近于整数的(x, y)解为(1, 1),对应的团簇式形式为[Cu-Cu12]Sn1Cu1=88.2Cu-11.8Sn (%),很好地解释了最常用的合金牌号C90800 (88Cu-12Sn)。

4 结论

本文总结了基于团簇加连接原子模型的固溶体近程有序结构描述以及相关的类分子团簇成分式。将Friedel振荡机制引入到团簇加连接原子模型中,建立了固溶体的电子结构模型,提出化学结构单元的概念,可以看作是合金中的分子式,是最小的电中性结构单元,用团簇加连接原子模型表示为团簇部分加上位于团簇间隙的连接原子部分,分别对应Friedel振荡势函数中的第一个波谷r1和第一个波峰r1.5位置。团簇之间没有搭接并且满足球周期序堆垛,相邻团簇位于Friedel振荡势函数的第三个波谷r3处。通过建立团簇在中程上的堆垛方式,给出了每个结构单元所包含原子个数Z的计算公式,Z与体系的平均原子密度ρa和团簇半径r1呈简单的正比例关系,Z=cρar13。通过计算,获得了最常用的二元铜基工业合金的化学结构单元,包括[Zn-Cu12]Zn4、[Cu-Cu12]Ni2Cu1、[Al-Cu12]Al2Cu3、[Cu-Cu12]Be2Cu2和[Cu-Cu12]Sn1Cu1,对应合金牌号分别为C26000 (70Cu-30Zn)、C70600 (90Cu-10Ni)、C60800 (92Cu-8Al)、C17200 (98Cu-2Be)和C90800 (88Cu-12Sn),是各体系中公认的性能最优的合金牌号。

来源--金属学报