分享：基于分形维数的模具钢电渣重熔铸坯碳偏析形貌特征研究

侯自兵, 曹江海, 常毅, 王伟, 陈晗

重庆大学材料科学与工程学院 重庆 400044

摘要

关键词： 偏析 ; 分形维数 ; 模具钢 ; 电渣重熔

由于电渣重熔工艺生产的金属材料具有纯净度高、组织致密、表面光洁等特点,通常采用该技术生产优质模具钢[1]。但与此同时,随着对产品质量要求的不断提高,实际生产中对电渣重熔铸坯缺陷的控制精细程度也不断提高[2]。H13模具钢属于一类重要的优质热作模具钢种,但由于对应的电渣重熔铸坯存在一定程度的C元素宏观/半宏观偏析(这也是困扰各类高品质碳钢质量提升的普遍问题),导致利用其生产高端产品的能力受到制约[1,3]。因此,为了能够更好更精细化地控制偏析缺陷,对H13模具钢电渣重熔铸坯的偏析特征进行更为细致的研究很有意义。

铸坯偏析现象是由于凝固过程中合金元素发生再分配而造成的[4]。分配系数K越小的元素,偏析越严重[4,5],对产品质量的影响也越大[6,7]。例如对于H13模具钢而言,C元素的含量不是最高,但由于其溶质分配系数较低,最后由偏析而造成碳化物分布不均匀等问题对产品的影响也相对最大[3]。基于测试方法,钢中C偏析的研究可分为成分含量与形貌2类。前者主要是基于钻孔取样化学分析、电子探针等方法实现,但这类方法存在无法观察形貌或分析范围太小的局限。对于后者,一般是先通过盐酸热酸洗的方法首先获得低倍组织;然后,由于酸液与铸坯接触发生反应时,C元素含量高的部分Gibbs自由能大,反应剧烈且颜色变黑,因此可通过对低倍组织中黑色区域识别偏析形貌。实际检测中,往往是基于元素宏观含量,或黑色偏析区域的大小、分布以及与宏观评级图对比结果来定性判别偏析程度并由此来指导工艺改进[8,9]。这些方法比较方便,但随着对高端钢铁产品质量要求的不断提高,现有整体成分的定量方法与以定性为主的偏析形貌描述方法已经难以满足精细化控制偏析及产品质量的目标。

本工作针对H13模具钢,尝试利用分形维数等新方法来定量研究不同熔速下铸坯内部不同位置的偏析形貌特征,从而服务于电渣重熔工艺的进一步优化与高端模具钢生产。分形是指某个图形的部分以某种形式与整体具有相似的形状,即图形的局部形态与整体形态相似,自相似性和标度不变性是分形的重要特征[10,11]。相比于实际检测中的常规方法,虽然偏析的面积与数目已经能够很好地定量描述偏析特征,但其并不能很好地反映偏析的轮廓形貌特征。研究表明,分形维数是定量表征复杂图形轮廓形貌特征的一种有效方法,它自20世纪70年代提出以来已被广泛地应用于不同的领域[12~16],铸坯组织形态描述是其中的一个应用方面[15,16]。对于铸坯的低倍组织,前人已采用分形维数来定量描述生长过程中显微组织[17~19],或单个奥氏体[20]、或球状等轴晶晶粒[21]、或单个组织数值模拟的结果[22,23],但到目前为止,利用分形维数来描述偏析形貌特征的研究尚未见报道。基于此,本工作重点引入分形维数方法来研究H13模具钢电渣重熔铸坯内偏析的形貌特征。

1 实验方法

实验用H13模具钢的主要化学成分(质量分数,%)为：C 0.38,Cr 4.98,Mo 1.33,V 0.99,Fe余量。对应电渣重熔铸坯横断面的尺寸为160 mm×160 mm。从铸坯中心纵断面取样,取样位置如图1所示。热酸洗实验中酸液为体积比1∶1的工业HCl水溶液,酸蚀温度60~80 ℃,酸蚀时间20 min。在得到整体中心面低倍组织后,沿铸坯中心线对称取12个位置点;在同样光源条件下利用高清数码相机得到每个位置点的凝固组织与偏析形貌,每个位置的尺寸为10 mm×10 mm。为了使研究结果更有代表性,共选取350和400 kg/h 2个熔速工艺下的铸坯进行热酸洗实验(熔速为电渣重熔过程中单位时间内熔化或凝固的合金质量)。

图1   铸坯中心纵断面取样位置示意图

Fig.1   Schematic of sampling location in the central plane of billet

在得到原始的低倍组织照片之后,利用图像处理软件Imag-Pro Plus 6.0对原始图像进行预处理。预处理过程包括转化成灰度图、锐化、去雾等环节。经过同样的预处理后,得到图像中的白色部分为铸坯的凝固组织,黑色部分则是铸坯的偏析区域。处理后的图片能清晰地区分出凝固组织与偏析区域,从而最大程度降低铸坯偏析形貌特征的定量分析误差。

对于铸坯偏析形貌特征的定量描述,本工作从C元素偏析点的面积数目与轮廓形貌分形特征展开。首先,利用图像处理软件Imag-Pro Plus 6.0对偏析单点与整体的面积进行计算。为了定量比较不同位置的偏析程度,引入偏析率(即所有偏析点面积之和与分析区域面积之比)来作为衡量偏析严重程度的判据之一。根据热酸洗原理[8,9],C元素偏析严重的区域,低倍组织图像中显现为黑色,因此该判据具有合理性。当偏析率越大时,对应位置整体的偏析程度越大。偏析率的计算方法如下式所示：

$\begin{array}{c}{?}_{\mathit{seg}}=\frac{{?}_{\mathit{seg}}}{{?}_{?}}\times 100\%\end{array}$(1)

式中,Rseg为偏析率,%;Aseg为所有偏析点面积之和,mm2;As为分析区域面积,mm2,本研究中即为100 mm2。与此同时,在分析过程中发现,存在不同尺寸的偏析点,因此基于偏析点的面积将偏析分为I、II、III 3种类型。3种类型对应的偏析面积分别为>0.1 mm2、0.01~0.1 mm2、<0.01 mm2,如图2所示。根据实际铸坯的偏析程度,本研究把I类归为大偏析点,III类归为小偏析点,II类处于二者之间。根据偏析点的大小,可由此计算不同类型偏析的数目比(不同类型偏析点数目与总偏析点数目之比)及面积比(不同类型偏析点面积与分析区域面积之比)。由于小偏析点对最终产品造成的危害相对较小,因此不同偏析点的数目比、面积比也可以作为衡量偏析程度的重要判据。例如,I类偏析点数目比或面积比越小,偏析点分布更弥散,成分更均匀,在后期的热处理加工等环节就更容易减轻或消除。另外,通过计算偏析点平均面积(所有偏析点总面积与其总数目之比)也可比较偏析点的弥散程度,即平均面积越小,弥散程度越大。

图2   I、II、III 3类不同大小偏析点示意图

Fig.2   Examples of I, II and III three kinds of segregation points (Area of I>0.1 mm2, 0.01 mm2<area of II<0.1 mm2,area of III<0.01 mm2)

然后,对于偏析点轮廓形貌的定量描述,采用经典的周长面积法[11~14]来计算某一区域内偏析点轮廓形貌对应的分形维数。先分别测量区域内所有偏析点的周长P与面积A;再以lnA为横坐标,以lnP为纵坐标作点状图,然后利用最小二乘法对图中所有数据点展开线性拟合并获得其斜率S;最后利用公式D=2S计算得到所观察区域的偏析点形貌的分形维数D。

2 实验结果与讨论

2.1 偏析形貌

图3和4分别为熔速为350和400 kg/h时铸坯内部不同位置的低倍组织图片,白色部分为凝固组织,黑色部分为偏析点。可知,2种熔速下,1# (图3a和4a)和12# (图3l和4l)试样的表面凝固组织呈现为柱状晶形貌;2# (图3b和4b)、3# (图3c和4c)、10# (图3j和4j)和11# (图3k和4k)试样的表面凝固组织为混晶区,即柱状晶与等轴晶转变区;4# (图3d和4d)、5# (图3e和4e)、6# (图3f和4f)、7# (图3g和4g)、8# (图3h和4h)和9# (图3i和4i)试样的表面凝固组织主要呈现为等轴晶形貌。不同位置的偏析形貌依凝固组织形貌的变化而变化。

图3   熔速为350 kg/h时铸坯内部不同位置的低倍组织

Fig.3   Macrostructures of samples 1#~12# (a~l) at different locations of billet under melting rate 350 kg/h

图4   熔速为400 kg/h时铸坯内部不同位置的低倍组织

Fig.4   Macrostructures of samples 1#~12# (a~l) at different locations of billet under melting rate 400 kg/h

2.2 偏析率及偏析点大小数目分布

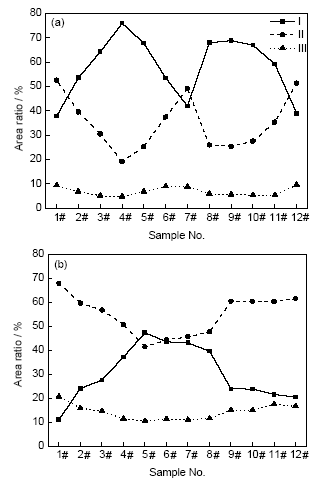
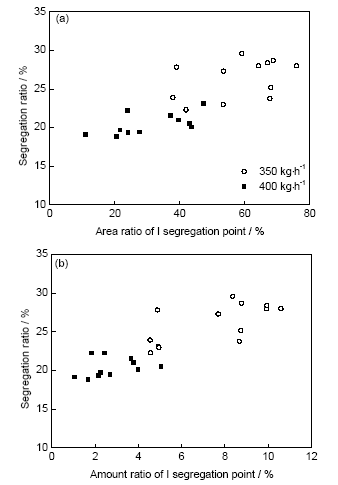
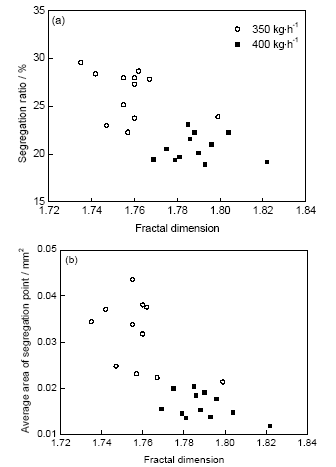
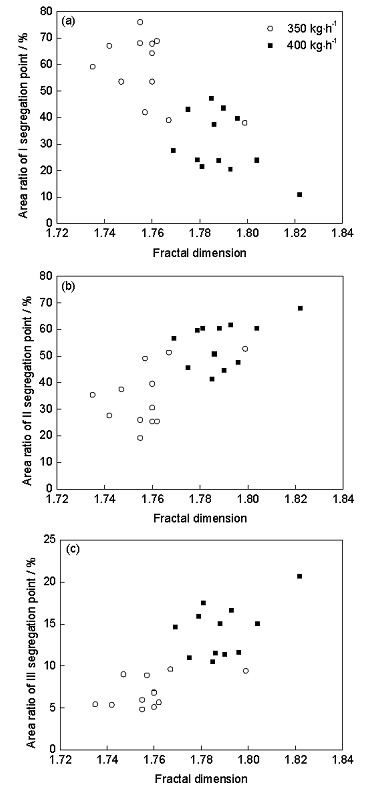
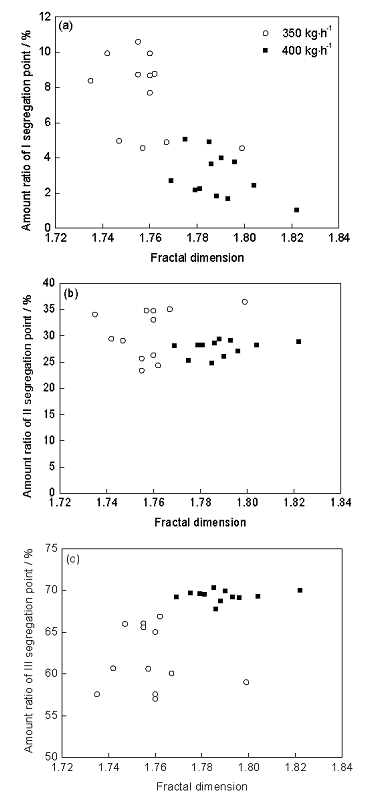
图5为熔速为350和400 kg/h时不同位置的偏析率。可以看出,由外往内,偏析率呈现先增加然后减小的趋势。图6为熔速为350和400 kg/h时不同位置I、II、III 3类偏析点的面积比的变化。图7为熔速为350和400 kg/h时不同位置I、II、III 3类偏析点的数目比的变化。可知,不同类型偏析点的面积比变化趋势差别较大,I类与II类偏析点的面积比变化剧烈(尤其是I类偏析点),且相互之间有对应的竞争关系,同时大部分位置明显大于III类偏析点的面积比;3类偏析点的数目比变化程度接近,I类偏析点的数目比最小,III类偏析点的数目比最大。这表明虽然大偏析点(如I类)所占数目比例小,但它能引起对应的偏析面积发生大的改变,且影响能力大于小偏析点。图8为不同位置偏析率与I类偏析面积比、数目比的变化关系。可知,随着I类偏析面积比、数目比的增加,偏析率呈现增加的趋势。因此,铸坯的整体偏析程度主要受大偏析点影响,且大偏析点越大或越多,偏析率越大。

图5   不同熔速下不同位置的偏析率

Fig.5   Segregation ratios at different locations under 350 and 400 kg/h

图6   不同位置I、II、III 3类偏析点的面积比

Fig.6   Area ratios of I, II and III three kinds of segregation points under 350 kg/h (a) and 400 kg/h (b)

图7   不同位置I、II、III 3类偏析点的数目比

Fig.7   Amount ratios of I, II and III three kinds of segregation points under 350 kg/h (a) and 400 kg/h (b)

图8   偏析率与I类偏析面积比和数目比的变化关系

Fig.8   Changes of segregation ratio with area ratio (a) and amount ratio (b) of I segregation point

2.3 分形维数

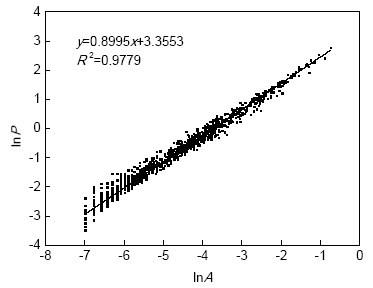
图9为熔速为350 kg/h时1#试样的lnP-lnA关系图,图中散点拟合直线的斜率为0.8995,拟合系数R2为0.9779。根据周长面积法,对应位置偏析点形貌的分形维数为1.799 (0.8995×2=1.799)。以此类推可计算不同位置的分形维数及对应的拟合系数,具体如表1所示。由于不同位置的拟合系数均很接近1,表明用分形维数这种方法来定量描述位置区域内所有偏析点形貌轮廓特征是有效的,且拟合系数越大,该位置内不同偏析点的形貌相似性越高。同时,当分形维数越大时,代表此位置内偏析点的轮廓形貌自相似复杂度越高。

图9   熔速为350 kg/h时1#试样lnP-lnA关系图

Fig.9   Relationship between lnP and lnA for fractal dimension of 1# sample under 350 kg/h (P—perimeter, A—area)

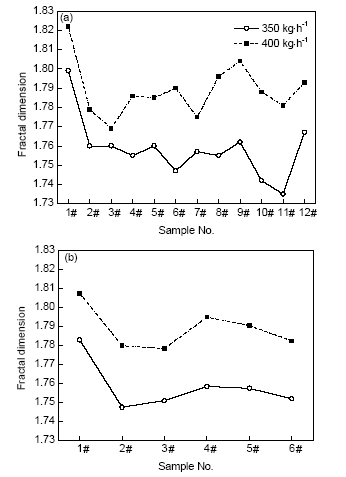
图10为熔速为350和400 kg/h时不同位置偏析形貌的分形维数及对应不同位置沿中心对称的平均分形维数。可见,不同熔速分形维数随位置的变化趋势基本一致,即从铸坯外部往内,先减小后增加然后再减小;同时沿中心对称左右侧的变化趋势也比较接近。分析图3、图4的凝固组织形貌与图10b的变化趋势发现,柱状晶等轴晶转变区与凝固终点等轴晶区的分形维数相对最小。

图10   不同熔速下不同位置的分形维数

Fig.10   Fractal dimensions at different locations under 350 and 400 kg/h(a) different locations (b) average value

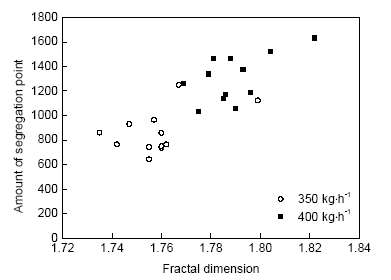
图11为熔速为350和400 kg/h时铸坯不同位置偏析率、偏析点平均面积随偏析分形维数的变化。可见,虽然整体上看偏析率随分形维数的增加有减小的趋势,但如单独观察某一个熔速的计算结果发现这种趋势并不明显。相比而言,对于偏析点平均面积,无论是单个熔速还是整体来看,其随着分形维数的增加而变小的趋势更为显著。图12和13分别为I、II、III 3类偏析面积比、数目比随分形维数的变化。可见,随着分形维数的增加,I类偏析点面积比减小,II和III类偏析点面积比增加;同时I类偏析的数目比减小趋势明显,III类偏析数目比有一定的增加趋势,II类偏析数目比变化不明显。图14为不同位置偏析点总数目随分形维数的变化。可见,随着分形维数的增加偏析点数目增加。综合以上,随着分形维数的增加,大偏析点的数目及所占面积减小,小偏析点数目及所占面积增加,且总偏析点数目呈现增加的趋势。

图11   偏析率、偏析点平均面积与分形维数的关系

Fig.11   Changes of segregation ratio (a) and average area of segregation point (b) with fractal dimension

图12   熔速为350和400 kg/h时I、II、III 3类偏析点面积比与分形维数的关系

Fig.12   Changes of area ratios of I (a), II (b) and III (c) three kinds of segregation points with fractal dimension

图13   熔速为350和400 kg/h时I、II、III 3类偏析点数目比与分形维数的关系

Fig.13   Changes of amount ratios of I (a), II (b) and III (c) three kinds of segregation points with fractal dimension

图14   熔速为350和400 kg/h时不同位置偏析点总数目与分形维数的关系

Fig.14   Changes of whole amount of segregation point at different locations with fractal dimension

因此,不同位置内偏析轮廓形貌的分形维数可作为衡量偏析点弥散程度的一个重要指标,即分形维数越大,对应区域内偏析点的分布越为弥散,大偏析点逐渐向小偏析点转变,铸坯C元素成分分布更为均匀。另外,柱状晶等轴晶转变区与凝固终点等轴晶区的分形维数较小,则这2个区域偏析点的尺寸分布的差异程度较大,大偏析点所占的面积比与数目比也较大,在以后控制偏析时需要注意这2个区域。

根据图3和4,由于无疏松等其它缺陷存在,区域内所有偏析点的轮廓形貌(周长)即为凝固组织的轮廓形貌(周长),则当偏析点的分形维数越大时,对应凝固组织轮廓形貌对应的自相似复杂程度越高。图3和4中的凝固组织主要为枝晶形态。当凝固过程中自相似枝晶的轮廓越为复杂时,固相间的相互连接将使液相偏析区域划分得更为弥散,难以形成大偏析区域;同时由于扩散距离的缩短,液相区溶质扩散阻力增加,根据成分过冷理论[15],此时液相区域更容易出现新的形核核心,因此将导致最终形成的偏析点更为弥散(区域内偏析点的平均面积更小)。对于图10b中分形维数较小值,可以推断,是由于柱状晶等轴晶转变区内柱状晶与等轴晶交叉存在,凝固组织之间形貌差异程度加大,导致对应的形貌自相似程度降低;而对于凝固终点等轴晶区,应是由于冷却速率相对最小,减弱了成分过冷程度,抑制了晶粒分枝的生长,从而降低了形貌复杂程度。

为了进一步研究分形维数的影响参量,对图3和4中每个位置内的二次枝晶间距进行测量。每个区域内分别选择3个典型枝晶,然后取其平均值。根据下式计算得到局部冷却速率[1]：

$\begin{array}{c}{?}_2=?{?}^{-?}\end{array}$(2)

式中,d2为二次枝晶间距,μm;R为局部冷却速率,℃/min;k取值为710;n取值为0.39。

再根据下式计算得到局部凝固时间[1]：

$\begin{array}{c}{?}_{\mathit{LS}}=\frac{{?}_{?}-{?}_{?}}{?}\end{array}$(3)

式中,tLS为局部凝固时间,min;Tl和Ts分别为钢的液相线温度(1482.5 ℃)和固相线温度(1407.5 ℃)。

图15为铸坯内不同位置的局部凝固时间。可见,整体而言,由外往内,凝固时间呈现增加趋势。图16为分形维数与局部凝固时间的散点图。分析发现二者并没有明显的正向或反向关系。自经典的凝固界面稳定性动力学理论(M-S理论)[24,25]被提出以来,凝固过程液固界面形态选择方面的研究已经取得了许多重要进展,但总体来说,纯扩散条件下液固界面的稳定性是由温度梯度、浓度梯度以及界面能3方面的因素共同决定,且凝固过程中的扰动频率受温度梯度、浓度梯度以及界面特征共同决定[26]。实际模具钢铸坯电渣重熔凝固过程界面的形成还会受液相流动等方面的影响,凝固组织类型也不单一,则其影响因素会表现得更为复杂[26]。因此,偏析点或凝固组织轮廓形貌的形成不仅仅由其凝固过程的温度参数(如局部凝固时间)决定,还受界面变化、偏析溶质元素分布、液相流动以及初始形貌等方面影响,因此若要更为准确地得到影响分形维数的凝固参量,还需要做更为精细化的研究。文献[15]也指出,分形维数不仅是用来描述不规则几何图形的几何参量,而且是一个依赖于不同物理参量的态函数。此外,也可以尝试利用分形维数来研究其它类型铸坯内偏析点的形貌特征。

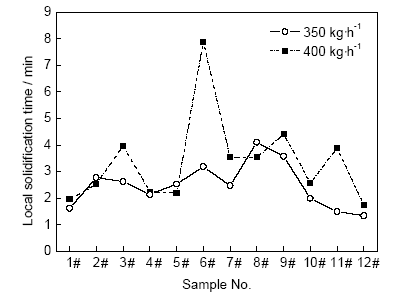
图15   铸坯内不同位置的局部凝固时间

Fig.15   Local solidification time at different locations in the billet

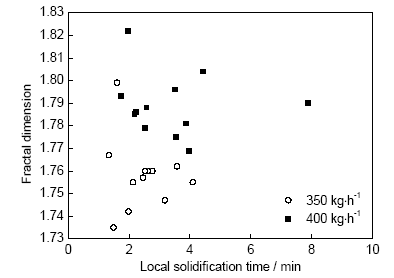
图16   分形维数与局部凝固时间的关系

Fig.16   Changes of fractal dimension with local soli-dification time

3 结论

(1) 铸坯的整体偏析程度主要受大偏析点影响,且大偏析点越大或越多,偏析率越大。

(2) 铸坯内偏析点形貌具有分形特征,并且分形维数可以作为衡量区域内偏析点弥散程度的一个重要指标,即分形维数越大,偏析点的分布越为弥散,大偏析点逐渐向小偏析点转变。

(3) 在柱状晶等轴晶转变区与凝固终点等轴晶区,偏析点的分形维数相对较小,易出现大偏析点。

来源--金属学报