分享：U65Fe30Al5非晶合金的纳米压痕蠕变行为研究

徐宏扬, 柯海波, 黄火根, 张培, 张鹏国, 刘天伟

中国工程物理研究院材料研究所 江油 621907

摘要

关键词： 非晶合金 ; 铀合金 ; 纳米压痕 ; 蠕变行为 ; 应力指数

蠕变主要表现为在特定温度和载荷条件下,材料随着时间的增长发生的缓慢变形,这种变形即使在应力小于屈服极限时仍具有不可逆性[1]。蠕变性能对于材料的应用至关重要,是影响材料失效的主要因素[1~4],因而掌握材料的蠕变性能参数非常必要。获取这类参数的常规方法是单轴拉伸蠕变测试法[5],但它需要大量的试样和较长的测试时间。与此不同,采用纳米压痕测试技术也能获得材料的蠕变性能指标[6,7],它既省时省料,对试样形态的要求也不高,且特别适用于薄膜、薄带等体积很小的材料以及难于加工的高硬、脆性材料[8,9]。

非晶合金是一类先进的金属材料[10],在航空航天、军事、体育等领域具有广阔的应用,因而其蠕变性能得到广泛关注。由于U金属的高密度和可裂变性,作为一个特殊的分支,铀基非晶合金在核工业领域具有重要的应用前景。尤其是,近期研究[11,12]表明,这类非晶合金的抗腐蚀性能和力学性能显著优于晶态铀合金,有望成为核相关领域的结构材料。但目前为止,这类材料的蠕变行为仍缺乏研究。

尽管铀基非晶合金自20世纪50年代开始已有报道[13],但由于早期形成的合金体系[14]非晶形成能力较弱,且热稳定性较差,难以开展系统的蠕变性能研究。近期,本课题组通过研究发现并制备出不同体系的稳定铀基非晶合金体系[11,12,15]。在本工作中,针对可形成单一非晶相的新型U-Fe-Al非晶合金,利用熔体甩带方法制备出高质量的非晶条带样品,采用纳米压痕测试技术研究了其蠕变性能,主要考察不同加载速率与载荷条件对蠕变行为的影响。

1 实验方法

实验选取的非晶合金成分为U65Fe30Al5 (原子分数,%)。实验原料为纯度均高于99.9%的金属U、Fe和Al。按照相应成分配料后, 采用NMS-II型小型亚稳合金制备炉, 在高纯Ar气(纯度>99.999%)保护下制备质量约5 g的母合金锭。为保证成分均匀, 反复熔炼母合金4次以上,破碎后用于Cu辊急冷甩带, Cu辊线速率约50 m/s, 顶吹气体压差约为0.04 MPa。最后获得尺寸为宽约2 mm、厚约30 μm的非晶条带样品,其形态和韧性参见文献[11]。为验证条带的非晶本质,利用EMPYREAN型X射线衍射仪(XRD,CuKα)进行测试。

本工作采用Hysitron TI 950纳米压痕系统微尺度蠕变测试,该仪器具有极高数据采集速率(最高至30000 s-1)、优异的位移和载荷分辨率(分别为1 nm和1 μN)[16]。测试时选择样品的自由面,即合金甩带时未直接与Cu辊接触的表面,因为在冷却过程中该面不会受Cu辊表面形态的影响,具有高的表面平整度和均匀度。测试前,首先保持样品自由面在上使其粘于平整洁净的金属样品台面,再使用丙酮对样品表面进行清洁处理,最后置于纳米压痕仪的样品台上。

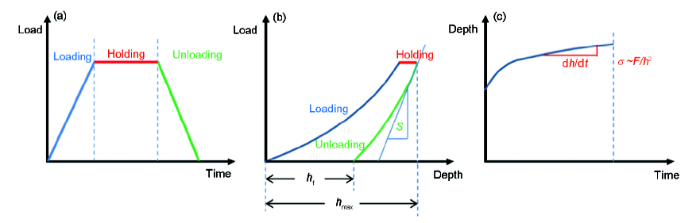
本工作的纳米压痕蠕变测试采用如图1a所示的加载函数,包括加载-保载-卸载3个阶段,单次蠕变测试获取的理想载荷-深度曲线如图1b所示,而理想的标准蠕变曲线(深度-时间曲线)如图1c所示。 测试方法包括等加载速率和等加载载荷2种,具体为：在20 mN/s加载速率下,选择载荷10、20、50、100和200 mN;在100 mN载荷下,选择加载速率2、5、10、20、50和100 mN/s 。对于单个加载载荷与加载速率,采取5次以上实验然后进行平均处理,以保证实验的重复性与可靠性。

图1   纳米压痕测试过程的加载函数与理想特征曲线

Fig.1   Loading function and ideal characteristic curves for nanoindentation creep (S—contact stiffness, h—indentation depth, F—load, hmax—maximum indentation depth, hf—permanent deformation depth after fully unloading, t—time, σ—stress)(a) load-time curve (b) load-depth curve (c) standard creep depth-time curve

2 实验结果

图2为U65Fe30Al5合金的XRD谱。可以看到,在30°~ 40°之间呈现出典型的馒头状非晶态漫散衍射峰特征, 确认该合金为单相的非晶结构。

图2   U65Fe30Al5非晶合金的XRD谱

Fig.2   XRD spectrum of U65Fe30Al5 amorphous alloy

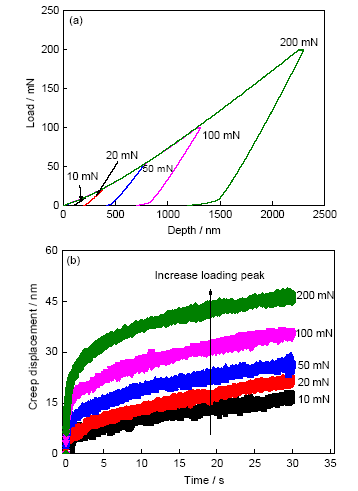
图3为U65Fe30Al5非晶合金以20 mN/s的速率加载至不同峰值载荷下的蠕变曲线。由图3a可见,样品的最大压入深度随着峰值载荷的增加不断增大,由10 mN下210 nm增至200 mN下的2300 nm,同时不同峰值载荷下加载阶段的载荷-深度曲线完全重合,表明该样品的成分与结构具有较好的均匀性,也表明实验数据具有很好的重复性和可靠性。图3b为载荷保持阶段即蠕变阶段样品蠕变位移随时间的变化曲线,为便于比较,起始蠕变位移和时间均进行了归零化处理(下同)。随着峰值载荷的增大,蠕变位移也不断变大,由10 mN下的15 nm增加至200 mN下的45 nm,且样品进入稳态蠕变的时间不断延长,由10 mN下的5 s变至200 mN下的10 s左右,这说明在较高的峰值载荷下,较大的压入深度引起更大的变形区域,为进入稳态蠕变需要在更大尺度上进行原子重排,因此所需的时间也更长。

图3   U65Fe30Al5非晶合金在不同载荷条件下蠕变30 s的载荷-深度曲线和蠕变位移-时间曲线(起始蠕变位移和时间进行归零化处理)

Fig.3   Load-depth (a) and creep displacement-time (b) curves during 30 s nanoindentation creeping under different peak loads (The curves in the Fig.3b are offset from the origin points of the creep process)

图4为U65Fe30Al5非晶合金在恒定峰值载荷(F=100 mN)不同加载速率条件下的蠕变曲线。其中图4a为载荷-深度曲线,为了能够清晰比较加载速率的效应,对不同加载速率的曲线进行了等间距平移处理。从中可见,在100 mN的载荷条件下,压头最大的压入深度约为1300 nm,随着加载速率的增加,保载阶段的蠕变位移也在增大,其中加载和卸载阶段的曲线保持平行,卸载段曲线可用于计算材料的模量,这说明该材料不同位置的模量保持不变,具有相对均匀的结构。图4b给出了蠕变位移随时间的变化曲线。可看出蠕变位移随着加载速率的增加而增大,由2 mN/s下的15 nm增大至100 mN/s下的40 nm。另外,在相同的载荷条件下,加载速率对材料进入稳态蠕变的起始时间影响并不大,基本都在5 s左右。

图4   U65Fe30Al5非晶合金在不同加载速率下蠕变30 s的载荷-深度曲线(平移处理后)和蠕变位移-时间曲线

Fig.4   Load-depth (a) and creep displacement-time (b) curves during 30 s nanoindentation creeping under different loading rates (Curves in Fig.4a are translation-transformed)

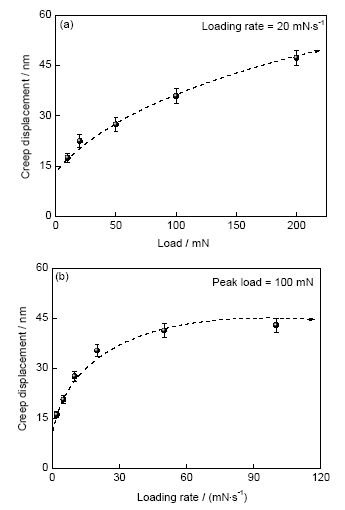
为了能够更加直观地比较加载速率与峰值载荷对蠕变行为的影响,根据图3和4可以获得U65Fe30Al5非晶合金蠕变30 s后蠕变位移值,该值随加载载荷与加载速率的变化趋势由图5给出。可以看出,在30 s的蠕变时间内,峰值载荷与加载速率的增大均会引起最终蠕变位移的增加,但两者之间仍有一些差别。一方面,当仅改变峰值载荷时,蠕变位移会随着峰值载荷增大一直增加(图5a),即使在200 mN的条件下仍未达到饱和。Ma等[17]研究了峰值载荷对CuZrAl和CuZrAlTi非晶薄膜的蠕变位移影响,其结果显示,随着峰值载荷从1 mN增大至16 mN,蠕变位移也会持续增大。Huang等[18]研究了峰值载荷对钛基非晶合金的蠕变行为影响,同样发现这种变化趋势。可见,这些工作与本实验的结果一致。这意味着峰值载荷对蠕变位移具有积极作用,随着峰值载荷的增加,材料在压头下的变形区域会一直增大,因为需要更大尺度内的原子局域重排以适应压头,由此引起蠕变位移的持续增加,这种变化趋势随着峰值载荷的加大很可能还会继续下去。另一方面,当仅改变加载速率时,蠕变位移则随着加载速率的增加先增大后基本恒定(图5b),其中当加载速率小于50 mN/s时,蠕变位移存在这种增长趋势,而当大于50 mN/s时,蠕变位移基本趋于饱和值45 nm,继续增大加载速率对最终蠕变位移的影响不大。Pang等[19]研究了加载速率对Cu49.3Zr50.7非晶合金蠕变位移的影响,发现在加载速率小于1 mN/s的条件下,蠕变位移一直呈增大趋势,但未报道更大加载速率下的实验结果。可见,在低加载速率情况下,本实验结果与文献[19]现象相符。

图5   U65Fe30Al5非晶合金的蠕变位移随载荷与加载速率的变化趋势

Fig.5   Variation of creep displacement versus peak load (a) and loading rate (b) during the nanoindentation creeping of U65Fe30Al5 amorphous alloy

3 讨论

在纳米压痕测试中,对于自相似的Beckvich压头测试,其应变率与应力满足以下标度关系[20,21]：

$\begin{array}{c}\dot{?}=\frac{1}{?}\frac{\mathit{dh}}{\mathit{dt}}\end{array}$(1)

$\begin{array}{c}\mathit{\sigma ~}\frac{?}{{?}^2}\end{array}$(2)

式中, $\begin{array}{c}\dot{?}\end{array}$为应变率,h为瞬时深度(即压头位移), $\begin{array}{c}?\end{array}$为应力,F为载荷,t为时间。在加载载荷条件下,h随t的变化可由以下经验方程进行描述[20]：

$\begin{array}{c}?={?}_0+?(?-{?}_0{)}^{?}+\mathit{kt}\end{array}$(3)

式中,h0和t0为蠕变起始点的压头深度与时间,a、b和k均为拟合参数。

对于稳态蠕变材料,应力与应变率之间满足以下关系[20]：

$\begin{array}{c}\dot{?}=?{?}^{?}\end{array}$(4)

式中,n为应力指数, C为常数。通过等温条件下 $\begin{array}{c}\mathit{lg}\dot{?}\end{array}$- $\begin{array}{c}\mathit{lg\sigma }\end{array}$曲线图的斜率可计算获得n。n表示材料稳态蠕变过程中应变率对应力的敏感度,可反映材料内部结构的信息。为了获得U65Fe30Al5非晶合金的n,用式(4)进行数据拟合。

图 6a为U65Fe30Al5非晶合金以20 mN/s加载至100 mN蠕变30 s的h-t拟合曲线。可见,拟合曲线与实验结果相吻合,拟合的相关系数R2 (=0.985)也接近1。图6b为在上述条件下的应力指数分析图。可以看出,在蠕变初始阶段,应力指数n高达282,说明此阶段的材料变形对应力极敏感,而当蠕变趋于稳态之后,应力指数n降至89,这一稳态值对应着此加载条件下材料的应力指数。

图6   U65Fe30Al5非晶合金蠕变过程中的实验与拟合曲线(式(3))和应力指数变化图

Fig.6   Experimental and fitting curve (Eq.(3)) (a) and the variation of stress exponent derived from stress-strain rate relationship curve (b) during the nanoindentation creeping of U65Fe30Al5 amorphous alloy (h0—initial creep displacement, t0—initial creep time, a and k—fitting parameters)

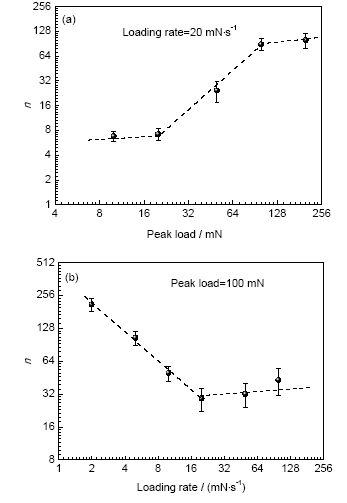
通过以上处理方法对其它所有蠕变曲线进行拟合(拟合后相关指数R2均大于0.96),获取U65Fe30Al5非晶合金在不同条件下的n值,它对载荷与加载速率的依赖关系由图7给出。由图7a可见,随着载荷的增大,n逐渐增大,其变化趋势可分为3段：当载荷低于20 mN时,n约为7;当高于100 mN时,n约为90;当大于20 mN而低于100 mN时,n由7快速增长至90。由图7b可知,随着加载速率的增大,n快速降低,当加载速率大于20 mN/s时,n基本不变,保持在40左右。对于非晶合金而言,Huang等[18]通过Ti基块体和条带样品的蠕变行为研究发现,相对于条带样品,块体样品具有更高的应力指数值,且随着接触深度即载荷的增大,应力指数会持续增大。这一结果与图7a中的现象一致。

图7   U65Fe30Al5非晶合金稳态蠕变过程中的应力指数-载荷曲线与应力指数-加载速率曲线

Fig.7   Curves of stress exponent-peak load (a) and stress exponent-loading rate (b) during the steady creeping of U65Fe30Al5 amorphous alloy(n—stress exponent)

目前,已经有很多研究报道了纳米压痕蠕变中加载速率与峰值载荷对应力指数的影响,包括一些晶态材料以及氧化物玻璃。例如对于纯的多晶Al和单晶Ni3Al,随着峰值载荷的增大,其蠕变过程会从原子扩散向位错攀爬并最终向滑动控制的蠕变逐渐演变,从而引起应力指数的显著改变[20]。但对于非晶合金,由于缺乏晶态合金中的位错等结构缺陷,变形行为一般根据“自由体积”[22]或者“剪切变形区”[23]模型进行解释,通常认为,随着峰值载荷的增加,其结构中的“自由体积”或“剪切变形区”体积会不断变化,进而引起应力指数的变化[19,20,24]。在纳米压痕测试中,由于压头形状的限制,材料中塑性变形一般局限在较小的体积中,并且具有非均匀应力场和强梯度应变场的特征,这会显著影响非晶合金中剪切变形区的演化,最终表现出压头周围剪切带形态的改变,从而引起应力指数的变化。这种行为已在锆基非晶合金[25]中得到证实,研究发现随着载荷的增大,压头周围变形区中剪切带图案会由较小区域向半圆形区域并最终向多剪切带交叉演化,并引起应力指数的改变。由此可见,对于非晶合金材料,应力指数与应力状态、剪切体积之间存在着密切的关系。

在增大载荷的条件下,非晶的变形更趋向非局域性,需要更大尺度与范围内的原子或剪切变形区进行重排适应,因而具有更大的应力指数,这与图7a结果一致。对于同一峰值载荷条件,不同的加载速率也会引起应力指数的变化,不过当快速加载时,特定应力条件下的最大剪切变形区域可能存在一个阈值,从而导致应力指数基本恒定,这也许是图7b现象的物理机制。

与常规晶态材料相比,非晶合金一般具有较高的应力指数[18,24,26]。几种不同材料的应力指数由表1给出。在近似相同的测试条件下,非晶合金和氧化物玻璃等无序体系的应力指数显著高于多晶氧化物B6O。例如对于钛基非晶,它经历了更大时间尺度的蠕变,但其应力指数(n=5)比B6O (n=0.14)的数值大了1个数量级。这意味着无序体系材料在应力作用下更容易发生变形,具有更强的应力敏感性,这可能与无序材料中具有更多的自由体积,原子堆积密度小于晶态材料有关。实际上,非晶合金的密度均低于同成分的晶态合金,存在着更多的自由体积区域,这些区域在外力作用下更易于变形,因而使得非晶合金材料具有更高的应力敏感性,即更大的应力指数。

4 结论

(1) U65Fe30Al5非晶合金的室温蠕变位移与峰值载荷、加载速率呈正相关性。

(2) 该非晶的应力指数与峰值载荷之间存在正相关性,随着载荷增加而增大,这主要跟参与剪切变形的体积增大有关。

(3) 该非晶的应力指数随加载速率的变化存在一个阈值,当低于该值时二者呈现负相关性,当高于该值时应力指数基本不变

来源--金属学报