分享：实用型数值回归法在三元铝合金互扩散系数计算中的应用

刘远荣, 陈伟民, 汤颖, 杜勇, 张利军

中南大学粉末冶金国家重点实验室, 长沙 410083

摘要

关键词： 铝合金 ; 扩散 ; 互扩散系数 ; 数值回归法

由于铝合金具有优异的力学性能, 被广泛应用于航空航天领域[1]和汽车[2]等国民经济领域. 实现铝合金制备过程微结构演变的定量描述是进行新型铝合金设计的核心. 研究[3~5]表明, 基于精准热力学和扩散动力学数据库的相场模拟, 是实现微结构演变定量描述的一种有效方法. 本研究小组经过数年努力, 建立了多元铝合金精准的热力学数据库[6]. 由于铝合金体系中, 尤其是三元及高组元合金缺乏精准的扩散系数实验数据, 故目前文献[7]报道的铝合金扩散动力学数据库并不完整. 为了进一步建立多元铝合金精准的扩散动力学数据库, 大量获得重要三元系铝合金精准的互扩散系数是当务之急.

固态半无限长型单相扩散偶常用于合金单相互扩散系数的测定[8~11]. 在三元系中, 一个物相对应有4个独立的互扩散系数, 包括2个主扩散系数和2个交叉扩散系数. 三元合金体系互扩散系数的测定, 一般采用传统的Matano-Kirkaldy (M-K) 方法[12~14]. 该方法要求必须有2组或以上的三元扩散偶, 并且2组扩散偶的扩散路径必须存在1个以上的交点. 虽然M-K方法可以获得交点处准确的互扩散系数, 但是测定效率低下, 无法满足当前材料基因组计划(materials genome initiative, MGI) 和集成计算材料工程 (integrated computational materials engineering, ICME) [15,16]的需求. 为了提高测定三元系互扩散系数的效率, 国内外不少科研工作者试图通过单一扩散偶获取三元合金的互扩散系数. 比如, Dayananda和Sohn[17], Zhang等[18], Jaques和LaCombe[19], Paul[20]均尝试采用单一扩散偶测定三元互扩散系数, 但这些方法或局限于平均扩散系数或仅局限于伪二元系的互扩散系数计算, 而未能取到较好的结果. 最近, 本研究小组通过理论推导及数学分析, 否定了前人采用单一扩散偶获得随成分变化扩散系数的可靠性[21], 并基于Fick第二定律和原子移动性概念发展了一种实用型数值回归法 (pragmatic numerical inverse method)[22]. 该方法的优点在于: (1) 可以获得三元系单一扩散偶沿整个扩散通道的互扩散系数; (2) 可以很方便地推广到多元系互扩散系数的计算. 目前, 该方法已成功应用于Co-Fe-Ni[22]和Cu-Ag-Sn[23]体系单相互扩散系数的测定. 采用该方法所测定的互扩散系数与传统M-K方法得到的结果非常吻合. 此外, 该方法可适用于不同类型的成分-距离曲线, 包含对称型、非对称型及含有零通量面等等, 表明该实用型数值回归法具有十分广泛的应用前景.

需要指出的是, 无论是传统的M-K方法还是上述实用型数值回归法, 目前仍多用于半无限长扩散偶的扩散系数计算. 而对于有限长 (或薄膜型) 扩散偶而言, 传统的M-K方法在计算元素互扩散通量时存在很大的不确定性, 因而会给后续互扩散系数的计算引入较大的误差[24]. 新提出的实用型数值回归法由于在计算过程中只需考虑初始条件及扩散时间、温度等参数, 理论上同样适用于有限长 (或薄膜型) 扩散偶中扩散系数的计算.

因此, 本工作选择bcc结构Al-Fe-Mn和fcc结构Al-Cu-Ni三元铝合金作为研究对象, 通过制备相应的固态单相扩散偶, 采用实用型数值回归方法, 高效测定2个体系随成分变化的互扩散系数. 对于Al-Fe-Mn体系, 共制备2组扩散路径上有交点的半无限长扩散偶, 而对于Al-Cu-Ni体系, 本工作制备2组扩散路径上无交点的半无限长扩散偶以及1组有限长 (或薄膜型) 扩散偶.

1 实验方法

采用纯度为99.99%的纯Al, Fe, Mn, Cu和Ni为原料, 在WKDHL型非自耗真空电弧炉中熔炼Al-Fe-Mn和Al-Cu-Ni体系合金, 2种合金名义成分如表1所示. 在半无限长扩散偶的制备过程中, 将熔炼好的合金切成5 mm×5 mm×10 mm的块体, 将块体真空封入石英管后在1273 K均匀化退火10 d并淬火. 将2块组成扩散偶的合金紧密贴合放入夹具中, 随后封入真空石英管, 加热到1273 K扩散退火48和49 h后淬火.

有限长扩散偶的制备过程与半无限长扩散偶的制备稍有区别. 首先将熔炼后的合金切成2 mm×5 mm×8 mm的片状, 真空封入石英管后加热到1273 K, 均匀化退火20 d并淬火. 将淬火后的合金块体厚度磨为约0.5 mm. 将组成扩散偶的两片合金紧密贴合后, 放入自主设计组装的高温真空热压机中. 在高纯Ar气保护下, 升温至1273 K保温32 h后, 关闭热源并通高速Ar气降温.

采用JXA-8230电子探针(EPMA)检测各扩散偶上垂直接触面的成分变化. 成分的测定在进行原子序数校正、吸收校正和荧光校正 (即ZAF校正) 后, 与标样的对比得出. 测量误差为1%~3%.

2 三元互扩散系数的计算方法及误差评估

2.1 新型数值回归方法

在A-B-C三元系中, 假定A和B是溶质元素而元素C是溶剂. Fick第一定律和第二定律表达式分别为:

$\begin{array}{c}{\tilde{J}}_i=-{{\tilde{D}}^C}_{\mathit{iA}}\frac{\partial c_A}{\partial x}-{{\tilde{D}}^C}_{\mathit{iB}}\frac{\partial c_B}{\partial x}\end{array}$(1)

$\begin{array}{c}\frac{\partial c_i}{\partial t}=\frac{\partial }{\partial x}\left({{\tilde{D}}^C}_{\mathit{iA}}\frac{\partial c_A}{\partial x}+{{\tilde{D}}^C}_{\mathit{iB}}\frac{\partial c_B}{\partial x}\right)\end{array}$(2)

式中, i为组元A或B. $\begin{array}{c}{\tilde{J}}_i\end{array}$表示组元i的互扩散通量, 即由元素互扩散引起的单位时间内垂直通过单位横截面积的i物质流量. ci为组元i的浓度. $\begin{array}{c}{\tilde{D}}_{\mathit{iA}}^C\end{array}$和 $\begin{array}{c}{\tilde{D}}_{\mathit{iB}}^C\end{array}$为三元系的互扩散系数, 分别表示在溶质A和B的浓度梯度下元素i的扩散系数. t为扩散时间, x为扩散距离.

根据绝对反应速率理论, 组元i的原子移动性参数Mi可以表示为[25]:

$\begin{array}{c}{M}_i=M_i^0\mathit{exp}\left(\frac{-Q_i}{\mathit{RT}}\right)\frac{1}{\mathit{RT}}\end{array}$(3)

式中, i为组元A, B或C, $\begin{array}{c}{M}_i^0\end{array}$为扩散指前因子, Qi为扩散激活能, R是气体常数, T为扩散温度. 为了减少可调参数的个数, Andersson和?gren[25]将 $\begin{array}{c}{M}_i^0\end{array}$和Qi合并为一个参数 $\begin{array}{c}\Delta G_i=-Q_i+\mathit{RTln}{M}_i^0\end{array}$. 则式(3)变为:

$\begin{array}{c}{M}_i=\frac{1}{\mathit{RT}}\mathit{exp}\left(\frac{\Delta G_i}{\mathit{RT}}\right)\end{array}$(4)

由式(4)可见, Mi直接与 $\begin{array}{c}\Delta G_i\end{array}$相关. 一般来说, 参数 $\begin{array}{c}\Delta G_i\end{array}$与合金的成分、温度和压力有关, 其表达式可由Redlich-Kister多项式展开得到:

$\begin{array}{c}\Delta G_i=c_A\Delta G_i^A+c_B\Delta G_i^B+c_C\Delta G_i^C+c_A{c}_B\Delta G_i^{A,B}+\end{array}\begin{array}{c}{c}_A{c}_C\Delta G_i^{A,C}+c_B{c}_C\Delta G_i^{B,C}+c_A{c}_B{c}_C\Delta G_i^{A,B,C}\end{array}$(5)

对于 $\begin{array}{c}\Delta G_i^j\end{array}$(i, j = A, B或C) , 当i=j时, $\begin{array}{c}\Delta G_i^j\end{array}$对应于组元i的自扩散系数; 当i≠j时, $\begin{array}{c}\Delta G_i^j\end{array}$对应于组元i在j中的杂质扩散系数. 一般来说, 纯元素的自扩散系数和杂质扩散系数可通过实验测定或理论计算确定. 参数 $\begin{array}{c}\Delta G_i^{A,B}\end{array}$, $\begin{array}{c}\Delta G_i^{A,C}\end{array}$, $\begin{array}{c}\Delta G_i^{B,C}\end{array}$以及 $\begin{array}{c}\Delta G_i^{A,B,C}\end{array}$分别表示组元i在A-B, A-C, B-C以及A-B-C体系中的相互作用参数, 其值一般与温度相关.

基于Manning[26]提出的random alloy模型, Chen等[22]将三元系的互扩散系数 $\begin{array}{c}{\tilde{D}}_{\mathit{ij}}^C\end{array}$和原子移动性参数Mi的关系表示为: $\begin{array}{c}{\tilde{D}}_{\mathit{ij}}^C=\mathit{RT}\left[M_i{?}_{\mathit{ij}}^C-c_i\left(M_A{?}_{\mathit{Aj}}^C+M_B{?}_{\mathit{Bj}}^C+M_C{?}_{\mathit{Cj}}^C\right)\right]+s{F}_V\end{array}$(6)

式中, MA, MB和MC分别表示组元A, B和C的原子移动性参数. FV表示空位流因子, 表征空位流效应对互扩散系数的贡献, s=0或1, 分别对应不考虑和考虑空位流贡献. $\begin{array}{c}{?}_{\mathit{ij}}^C\end{array}$, $\begin{array}{c}{?}_{\mathit{Aj}}^C\end{array}$, $\begin{array}{c}{?}_{\mathit{Bj}}^C\end{array}$和 $\begin{array}{c}{?}_{\mathit{Cj}}^C\end{array}$均表示热力学因子, 表征三元系A-B-C的热力学对相应互扩散系数的影响程度, 其标准定义为:

$\begin{array}{c}{?}_{\mathit{ij}}^C=\frac{c_i}{\mathit{RT}}?\left(\frac{\partial {\mu }_i}{\partial c_j}-\frac{\partial {\mu }_i}{\partial c_C}\right)\end{array}$(7)

式中, μi表示组元i的化学势, ci和cj分别为组元i和j的浓度, cC为溶剂元素C的浓度. 采用文献[6]中已有的多元铝合金体系精准热力学数据库, 可以获得本工作所需要的热力学因子.

在计算过程中, 从实验测定或理论计算获得 $\begin{array}{c}\Delta G_i^j\end{array}$, 而将相互作用参数作为可调参数. 联立式(2)~(7)可以模拟给定的扩散偶在一定扩散时间后的成分-距离曲线. 将该模拟值与实验测定的成分-距离曲线值的差值作为优化对象, 运用编程迭代的方法进行优化, 即当2者之间的差别最小时, 认为该组可调参数最合理. 将该组参数应用于式(5), 并联立式(4)~(7), 可得到该扩散偶上任意成分点的互扩散系数. 值得注意的是, 所获得的三元互扩散系数必须同时满足以下3个热力学稳定条件[27]:

$\begin{array}{c}{\tilde{D}}_{\mathit{AA}}^C+{\tilde{D}}_{\mathit{BB}}^C>0\end{array}$

$\begin{array}{c}{\tilde{D}}_{\mathit{AA}}^C?{\tilde{D}}_{\mathit{BB}}^C-{\tilde{D}}_{\mathit{AB}}^C{\tilde{D}}_{\mathit{BA}}^C\ge 0\end{array}$

$\begin{array}{c}{\left({\tilde{D}}_{\mathit{AA}}^C-{\tilde{D}}_{\mathit{BB}}^C\right)}^2+4{\tilde{D}}_{\mathit{AB}}^C{\tilde{D}}_{\mathit{BA}}^C\ge 0\end{array}$(8)

式中, $\begin{array}{c}{\tilde{D}}_{\mathit{AA}}^C\end{array}$和 $\begin{array}{c}{\tilde{D}}_{\mathit{BB}}^C\end{array}$分别表示三元系中A和B的主扩散系数, 而 $\begin{array}{c}{\tilde{D}}_{\mathit{AB}}^C\end{array}$和 $\begin{array}{c}{\tilde{D}}_{\mathit{BA}}^C\end{array}$表示三元系中A和B的交叉扩散系数.

2.2 误差评估方法

所测定的互扩散系数误差均通过误差传递方法[28]进行计算. Léchelle等[28]认为, 方程f(A1, B1)的误差u(f(A1, B1))是通过参数A1的误差u(A1)和B1的误差u(B1)进行传递的, 即:

$\begin{array}{c}u\left(f\left(A_1,B_1\right)\right)=\sqrt{{\left(\frac{\partial f}{\partial A_1}\right)}^2{\left(u\left(A_1\right)\right)}^2+{\left(\frac{\partial f}{\partial B_1}\right)}^2{\left(u\left(B_1\right)\right)}^2}\end{array}$(9)

式中, A1和B1等表示方程f的参数 (如: 组元浓度).

数值回归法计算互扩散系数的误差来源主要为实验测量. 一般认为, EPMA的相对误差为2%, 高温炉温度相对误差为0.5%. 这2部分误差首先传递到 $\begin{array}{c}{?}_{\mathit{ij}}^C\end{array}$和Mi. 其次, 误差通过式(6)传递给 $\begin{array}{c}{\tilde{D}}_{\mathit{ij}}^C\end{array}$(i, j=A, B). 最后, 通过Fick第二定律表达式模拟成分-距离曲线, 考虑与实验数据的差别, 从而最终确定互扩散系数的误差.

3 结果与讨论

3.1 bcc结构Al-Fe-Mn合金扩散系数

基于本研究组建立的热力学数据库[6], 采用实用型数值回归法获得了C1和C2扩散偶整个扩散路径上的三元互扩散系数. 由于C1和C2为采用相同方法制备的bcc结构Al-Fe-Mn扩散偶, 相同成分处的互扩散系数理论上应相同. 为满足这一条件, 在数值回归法计算中采用相同的参数. 图1为采用本工作得到的扩散系数模拟的C1和C2扩散偶的成分-距离曲线与实验测定值的对比. 可以看出, 2组扩散偶的成分-距离曲线模拟值与实验值基本符合, 说明了本工作测定的互扩散系数 $\begin{array}{c}{\tilde{D}}_{\mathit{AlMn}}^{\mathit{Fe}}\end{array}$的合理性和准确性.

图1   bcc结构Al-Fe-Mn扩散偶C1和C2在1273 K的成分-距离曲线

Fig.1   Comparison between simulated and experimental concentration profiles of bcc structured Al-Fe-Mn diffusion couples C1 (a) and C2 (b) at 1273 K

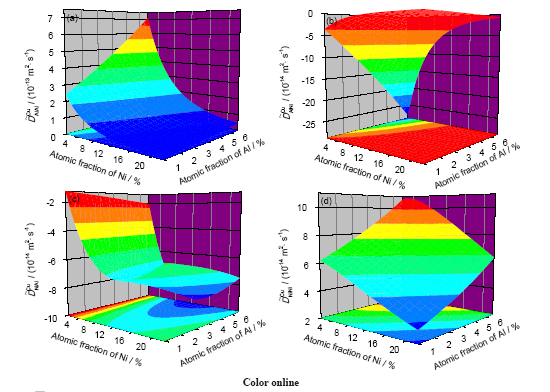
将互扩散系数随溶质元素Al和Mn含量的变化绘制成三维互扩散系数图, 如图2所示. 通过误差传递方法计算所测定的bcc结构Al-Fe-Mn相互扩散系数的平均误差为8%. 从图2a可以看出, Al的主扩散系数 $\begin{array}{c}{\tilde{D}}_{\mathit{AlAl}}^{\mathit{Fe}}\end{array}$呈现出近似以Al成分的中点对称的趋势. 对比图2a和d还可发现, Al的主扩散系数 $\begin{array}{c}{\tilde{D}}_{\mathit{AlAl}}^{\mathit{Fe}}\end{array}$和Mn的主扩散系数 $\begin{array}{c}{\tilde{D}}_{\mathit{MnMn}}^{\mathit{Fe}}\end{array}$在数值上相近, 且均为受Mn含量影响比受Al含量的影响大. 而Al的交叉扩散系数, 是表征三元系Al-Fe-Mn扩散过程中Mn的浓度梯度对Al的互扩散通量的影响, 与Al和Mn成分均相关(图2b). 但图2c显示, Mn的交叉扩散系数 $\begin{array}{c}{\tilde{D}}_{\mathit{MnAl}}^{\mathit{Fe}}\end{array}$基本不受Al影响.

图2   实用型数值回归法计算的bcc结构Al-Fe-Mn合金在1273 K的4个互扩散系数与Al和Mn成分的关系

Fig.2   Four kinds of composition-dependent interdiffusivities of bcc structured Al-Fe-Mn alloys determined by the pragmatic numerical inverse method at 1273 K

(a) Al main interdiffusivity $\begin{array}{c}{\tilde{D}}_{\mathit{AlAl}}^{\mathit{Fe}}\end{array}$(b) Al cross interdiffusivity $\begin{array}{c}{\tilde{D}}_{\mathit{AlMn}}^{\mathit{Fe}}\end{array}$(c) Mn cross interdiffusivity $\begin{array}{c}{\tilde{D}}_{\mathit{MnAl}}^{\mathit{Fe}}\end{array}$(d) Mn main interdiffusivity $\begin{array}{c}{\tilde{D}}_{\mathit{MnMn}}^{\mathit{Fe}}\end{array}$

3.2 fcc结构Al-Cu-Ni合金扩散系数

3.2.1 半无限长扩散偶 图3为fcc结构Al-Cu-Ni半无限长扩散偶K1和K2的扩散路径图. 可以看出, K1和K2在扩散路径上没有交点. 因此, 采用传统的M-K法不能获得其互扩散系数. 但实用型数值回归法可以非常方便地计算随成分变化的扩散系数. 同样, 由于K1和K2是采用相同方法制备的半无限长扩散偶, 所以相同成分处的扩散系数应保持一致. 为了确保互扩散系数的一致性, 本工作在计算互扩散系数时采用相同的参数. 通过耦合Al-Cu-Ni体系热力学描述[6], 本工作采用实用型数值回归法计算得到了fcc结构Al-Cu-Ni合金随成分变化的互扩散系数. 图4为采用本工作得到的互扩散系数模拟的扩散偶K1和K2成分-距离曲线与实验值的对比. 可以看出, 模拟值与实验测定值符合得很好, 说明了本工作获得的互扩散系数的合理性和准确性.

图3   fcc结构Al-Cu-Ni半无限长扩散偶在1273 K时的扩散路径图

Fig.3   Diffusion paths of two fcc structured Al-Cu-Ni semi-infinite diffusion couples at 1273 K

图4   fcc结构Al-Cu-Ni半无限长扩散偶K1和K2在1273 K的成分-距离曲线

Fig.4   Comparison between simulated and experimental concentration profiles of fcc structured Al-Cu-Ni semi-infinite diffusion couples K1 (a) and K2 (b) at 1273 K

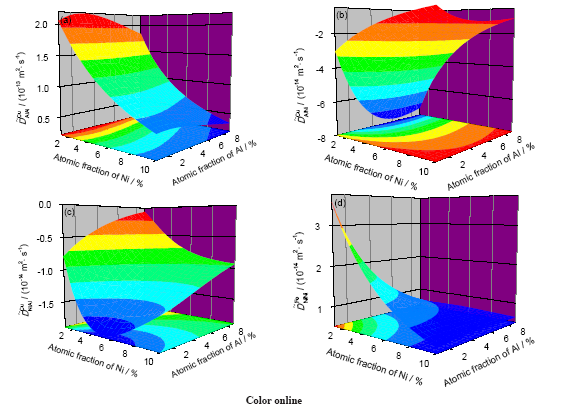
将互扩散系数随溶质元素Al和Ni含量的变化绘制成三维互扩散系数图, 如图5所示. 经误差传递分析, 互扩散系数的误差为7%. 从图5a和d可以看出Al的主扩散系数 $\begin{array}{c}{\tilde{D}}_{\mathit{AlAl}}^{\mathit{Cu}}\end{array}$和Ni的主扩散系数 $\begin{array}{c}{\tilde{D}}_{\mathit{NiNi}}^{\mathit{Cu}}\end{array}$均受Al和Ni含量的共同影响, 并且Ni含量对Al的主扩散系数 $\begin{array}{c}{\tilde{D}}_{\mathit{AlAl}}^{\mathit{Cu}}\end{array}$的影响比Al的大.

图5   实用型数值回归法计算的fcc结构Al-Cu-Ni合金在1273 K的4个互扩散系数与Al和Ni成分的关系

Fig.5   Composition-dependent interdiffusivities $\begin{array}{c}{\tilde{D}}_{\mathit{AlAl}}^{\mathit{Cu}}\end{array}$ (a), $\begin{array}{c}{\tilde{D}}_{\mathit{AlNi}}^{\mathit{Cu}}\end{array}$ (b), $\begin{array}{c}{\tilde{D}}_{\mathit{NiAl}}^{\mathit{Cu}}\end{array}$ (c) and $\begin{array}{c}{\tilde{D}}_{\mathit{NiNi}}^{\mathit{Cu}}\end{array}$ (d) of fcc structured Al-Cu-Ni alloys determined by the pragmatic numerical inverse method at 1273 K

3.2.2 有限长 (或薄膜型) 扩散偶 K3扩散偶在1273 K扩散退火32 h后, EPMA检测的成分-距离曲线如图6所示. 由图可知, 在x=0处, Al的成分为8.7%, 已明显低于初始成分 (即: Cu-9.5%Al) . 这说明扩散偶Cu-Al合金端的Al已经扩散并影响了端际成分. 这种情况下Al的互扩散通量不能直接由成分-距离曲线确定.

对于有限长扩散偶而言, 扩散退火后端际成分的变化导致传统M-K方法在计算元素互扩散通量方面存在一定的不确定性, 从而给计算得到的互扩散系数引入较大的误差[24]. 然而, 实用型数值回归法在计算过程中并不涉及元素通量, 而只是模拟从初始条件开始至扩散退火结束整个过程中互扩散系数导致的成分-距离曲线变化, 所以能有效计算有限长扩散偶的互扩散系数. 本工作采用数值回归法计算得到了扩散偶K3的互扩散系数, 并且所有互扩散系数均满足热力学稳定条件 (公式(7)) . 如图6所示, 由本工作得到的互扩散系数模拟的成分-距离曲线与实验测定值符合得很好, 说明数值回归法计算有限长扩散偶的互扩散系数是简单且合理的.

图6   fcc结构Al-Cu-Ni有限长扩散偶K3在1273 K时的成分-距离曲线

Fig.6   Comparison between simulated and experimental concentration profiles of fcc structured Al-Cu-Ni finite diffusion couple K3 at 1273 K

图7为本工作获得的有限长扩散偶K3的互扩散系数随Al和Ni含量变化趋势图. 由误差传递方法计算的互扩散系数误差为10%. 从图7a和d中可看出, Al的主扩散系数 $\begin{array}{c}{\tilde{D}}_{\mathit{AlAl}}^{\mathit{Cu}}\end{array}$整体上大于Ni的主扩散系数 $\begin{array}{c}{\tilde{D}}_{\mathit{NiNi}}^{\mathit{Cu}}\end{array}$, 这与图6中Al的扩散距离大于Ni的扩散距离这一结果相符. 另外, Al和Ni含量均影响Al的主扩散系数 $\begin{array}{c}{\tilde{D}}_{\mathit{AlAl}}^{\mathit{Cu}}\end{array}$且Ni含量影响显著, 而Ni的主扩散系数 $\begin{array}{c}{\tilde{D}}_{\mathit{NiNi}}^{\mathit{Cu}}\end{array}$受Al和Ni含量的共同影响.

图7   实用型数值回归法计算的fcc结构Al-Cu-Ni有限长扩散偶在1273 K的4种互扩散系数与Al和Ni成分的关系

Fig.7   Composition-dependent interdiffusivities $\begin{array}{c}{\tilde{D}}_{\mathit{AlAl}}^{\mathit{Cu}}\end{array}$ (a), $\begin{array}{c}{\tilde{D}}_{\mathit{AlNi}}^{\mathit{Cu}}\end{array}$ (b), $\begin{array}{c}{\tilde{D}}_{\mathit{NiAl}}^{\mathit{Cu}}\end{array}$ (c) and $\begin{array}{c}{\tilde{D}}_{\mathit{NiNi}}^{\mathit{Cu}}\end{array}$ (d) of fcc structured Al-Cu-Ni finite diffusion couple determined by the pragmatic numerical inverse method at 1273 K

3.2.3 结果对比 本工作设计了fcc结构Al-Cu-Ni半无限长和有限长 (或薄膜型) 2种类型的扩散偶. 为定量对比互扩散系数的差别, 引入一个差值百分比变量 $\begin{array}{c}E=\frac{{\tilde{D}}^{\mathit{semi}}-{\tilde{D}}^{\mathit{finite}}}{{\tilde{D}}^{\mathit{semi}}}\times 100\%\end{array}$(其中 $\begin{array}{c}{\tilde{D}}^{\mathit{semi}}\end{array}$为半无限长型扩散偶的互扩散系数, $\begin{array}{c}{\tilde{D}}^{\mathit{finite}}\end{array}$为有限长扩散偶的互扩散系数). 采用实用型数值回归法计算得到的Al-Cu-Ni合金2种扩散偶的互扩散系数差值百分比与Al和Ni含量之间关系的三维图如图8所示. 可以看出, 采用半无限长扩散偶得到的Al主扩散系数 $\begin{array}{c}{\tilde{D}}_{\mathit{AlAl}}^{\mathit{Cu}}\end{array}$和Ni主扩散系数 $\begin{array}{c}{\tilde{D}}_{\mathit{NiNi}}^{\mathit{Cu}}\end{array}$几乎均大于有限长扩散偶得到的值. 计算显示, $\begin{array}{c}{E}_{\mathit{AlAl}}^{\mathit{Cu}}\end{array}$的绝对值在72%以内, $\begin{array}{c}{E}_{\mathit{NiNi}}^{\mathit{Cu}}\end{array}$的值小于93%. 以上数据表明2种扩散偶的互扩散系数相差略大, 但是基本保持在一个数量级内.

图8   fcc结构Al-Cu-Ni半无限长和有限长扩散偶互扩散系数差值百分比图

Fig.8   Comparison of the computed interdiffusivities$\begin{array}{c}{E}_{\mathit{AlAl}}^{\mathit{Cu}}\end{array}$ (a), $\begin{array}{c}{E}_{\mathit{AlNi}}^{\mathit{Cu}}\end{array}$ (b), $\begin{array}{c}{E}_{\mathit{NiAl}}^{\mathit{Cu}}\end{array}$ (c) and $\begin{array}{c}{E}_{\mathit{NiN}i}^{\mathit{Cu}}\end{array}$ (d) in semi-infinite and finite diffusion couple in fcc structured Al-Cu-Ni alloys

究其原因, Al-Cu-Ni半无限长和有限长扩散偶虽然同属于fcc单相区, 但是扩散偶的制备过程却有明显差别. 在半无限长扩散偶制备过程中将合金放入夹具中并施加一定压力, 而有限长扩散偶仅由一个石墨块体 (约13.5 g) 施力, 扩散偶保持较紧密的接触. 因此, 2种扩散偶所受外部压力有明显差别. 一般认为, 扩散偶外部压力会影响扩散偶中元素的扩散, 从而导致这2种扩散偶得到的扩散系数不一致.

4 结论

(1) 采用固态单相扩散偶方法制备了2个bcc结构Al-Fe-Mn扩散偶, 利用EPMA获得扩散偶的成分-距离曲线, 并通过耦合精准热力学数据库的实用型数值回归法计算得到了该体系在1273 K随成分变化的互扩散系数. 由所得扩散系数模拟的Al-Fe-Mn体系扩散偶的成分-距离曲线与实验值高度符合, 表明本工作所得随成分变化互扩散系数的准确性.

(2) 制备了3个fcc结构Al-Cu-Ni扩散偶, 其中半无限长型2个, 有限长型 (或薄膜型) 1个. 利用EPMA检测和实用型数值回归法计算获得了半无限长和有限长 (或薄膜型) 扩散偶的互扩散系数. 所有计算的互扩散系数均满足热力学稳定条件, 并且能通过模型计算重现各扩散偶的成分-距离曲线. 分析结果表明, 数值回归法可以处理扩散通道上无交点的扩散偶和有限长扩散偶这类问题, 从而弥补传统方法 (如Matano-Kirkaldy方法) 的缺陷.

来源--金属学报