分享:挤压态ZK60镁合金室温拉-压不对称性研究
太原科技大学应用科学学院, 太原 030024
摘要
基于室温轴向拉伸和压缩实验研究了挤压态ZK60镁合金的拉-压不对称性. 通过修正黏塑性自洽模型, 建立了耦合滑移和孪生的晶体塑性力学模型, 模拟了挤压态ZK60镁合金轴向拉,压力学行为, 分析了基面,柱面,锥面滑移及{1012}<1011>拉伸孪生和{1011}<1012>压缩孪生在塑性变形过程中的激活及演变情况. 结合实验与模拟, 从微观塑性变形机制角度分析了具有初始挤压态丝织构的镁合金产生拉-压不对称性的机理. 结果表明: 轴向拉伸过程中拉伸孪生和压缩孪生都较难激活, 变形初期以基面滑移为主, 由于基面滑移取向因子较低, 导致屈服应力较高; 随着晶粒转动, 基面滑移分切应力降低, 应力逐步升高, 变形机制转为以柱面滑移为主, 辅以锥面<c+a>滑移, 应变硬化率较低, 应力-应变曲线较平稳. 轴向压缩前期, 临界剪切应力较低的拉伸孪生大量激活, 导致屈服应力较低; 应变达到6.0%后拉伸孪生逐渐饱和, 相对活动量快速降低, 硬化率迅速提高, 由于大量孪晶界对位错滑移形成阻碍, 滑移机制未出现大量激活; 轴向压缩后期, 随着应力的持续升高, 压缩孪生启动, 相对活动量迅速上升, 塑性变形积累的应力得以释放, 硬化率降低. 因此, 挤压丝织构状态决定了镁合金在室温轴向拉,压变形过程中的变形机制存在明显区别, 从而导致挤压镁合金产生显著的轴向拉-压不对称性.
关键词:
镁合金具有密度低,比强度和比刚度高,导热导电性好,易回收且电磁屏蔽性能优越等优点, 在交通,通讯和航空航天等领域有广阔的应用前景, 被誉为"21世纪绿色工程材料"[1~3]. 目前, 工业上多以铸态镁合金为主, 与铸态镁合金相比, 变形镁合金的晶粒细小,组织均匀, 具有更好的综合力学性能[4]. 但镁合金室温下独立滑移系较少, 且各滑移系开动的临界剪切应力(CRSS)差别很大, 使得镁合金在挤压过程中易形成强烈的(0002)基面平行于挤压方向的基面丝织构, 表现出明显的拉-压不对称性[5,6]. 拉-压不对称性主要表现在屈服不对称性和塑性硬化行为不对称性2方面. 轴向压缩时屈服应力低, 而轴向拉伸时屈服应力高, 且拉,压应力-应变曲线形状差异很大. 拉-压不对称性的存在一定程度上限制了镁合金在结构件上的应用, 尤其是同时承受拉伸和压缩应力的一些结构件(如支撑横梁). 因此, 研究镁合金室温拉-压不对称性的微观机理, 对开发高性能变形镁合金结构材料, 拓展工业广泛应用具有现实意义.
近年来, 各国学者对镁合金拉-压不对称性作了较多的研究, 取得了一定的进展. Chino等[7]在不同温度下对AZ31镁合金挤压棒材进行了单向拉伸-压缩实验, 结果表明, 对于强烈丝织构状态的镁合金, 拉伸孪生会对拉-压不对称性产生重要影响. 王渠东等[8]研究了往复挤压变形对镁合金拉伸,压缩屈服不对称性的影响, 认为通过细化组织和改变织构能显著降低镁合金拉-压强度差异性. Lin等[6]利用单向压缩实验, 研究了挤压态ZK60镁合金的室温各向异性, 结果表明, 镁合金强烈的丝织构和hcp结构的低对称性是造成镁合金产生拉-压不对称的原因.
目前, 对于挤压态镁合金拉-压力学行为不对称性的研究仍缺乏较深入的理论依据. 本工作基于室温轴向拉伸和压缩实验对挤压态ZK60镁合金进行了拉-压不对称性研究, 并通过修正黏塑性自洽模型, 建立了耦合滑移和孪生的晶体塑性力学模型, 在该模型中, 孪生机制同时考虑了拉伸孪生和压缩孪生. 利用修正的模型对实验进行了数值模拟, 结合实验, 从微观变形机制的角度分析了具有初始挤压丝织构镁合金产生拉-压不对称性的机理.
1 实验和模拟方法
1.1 实验方法
实验材料为挤压态ZK60镁合金, 由直径100 mm的铸态坯料在800 t卧式挤压机上挤压成直径30 mm的棒材, 挤压比为11. 挤压态合金的主要化学成分(质量分数, %)为Mg-5.5Zn-0.5Zr. 采用Philips PW1820型X射线衍射仪(XRD)进行宏观织构测试. 图1所示为挤压态ZK60镁合金(0002)极图和拉伸,压缩试件取样示意图. 室温力学性能测试在Zwick万能材料试验机上进行, 片状拉伸试样标距为10 mm×3 mm×1.5 mm, 压缩试样的尺寸为8 mm×5 mm×5 mm, 力学性能测试采用相同的应变速率. 纵截面金相组织采用LEICA MEF4M 型显微镜观察.
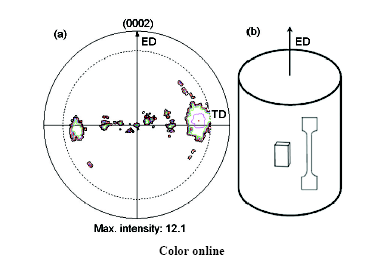
图1 挤压态ZK60镁合金(0002)基面极图和拉伸,压缩试件示意图
Fig.1 Measured (0002) pole figure (a) and schematic of the tensile and compression samples (b) of as-extruded ZK60 magnesium alloy (ED--extrusion direction, TD--transverse direction)
1.2 黏塑性自洽模型
黏塑性自洽(viscoplastic self-consistent, VPSC)模型是由Molinari等[9]提出的, 之后Lebensohn和Tomé[10,11]利用该模型对金属材料塑性变形过程进行了数值模拟, 并对其各向异性作了合理解释, 使该模型得到了发展. 该模型考虑了多晶体中晶粒之间的相互作用, 假设多晶体晶粒为椭球体夹杂深埋在无限大的均匀介质中(homogeneous equivalent medium, HEM)[12], 模型采用了率相关的连续本构模型方程[13,14]:
式中, 和分别为应变速率偏张量和应力偏张量; s表示每个滑移和孪生机制; 为Schmid 对称张量, 垂直于滑移或孪生面, 为Burgers矢量或孪生剪切方向; 为剪切率; 为参考剪切率; 为黏塑性约定, 能够将宏观应变率和宏观偏应力联系起来; 为各变形机制的临界剪切应力, 控制着各变形机制的开启. 随变形的进行而不断变化, 具体演化规则可用Voce硬化模型[13,14]描述:
式中, 和分别为机制s的初始和外推临界剪切应力; 和分别为机制s的初始和渐进硬化率; 为晶体中的累计塑性剪力, 其表达式为:
式中, 为切应变增量.
VPSC模型能够同时考虑滑移和孪生2种变形机制[9]. 本工作采用主导孪生旋转(predominant twinning reorientation, PTR)等模型计算变形过程中孪晶对晶粒旋转的贡献. PTR模型是由Tomé等[15]首先提出来的. 在每个增量步中, 晶粒g中孪晶系的孪晶分数可用下式[13~15]计算:
式中, 是孪晶系的临界剪切应变, 是孪晶系的特征剪应变. 对所有孪晶系的孪晶分数之和进行叠加得到总的孪晶分数, 如下式[14]所示:
通过对每个增量步的孪晶分数进行叠加, 用得到的累计孪晶分数与孪晶引起晶粒旋转的门槛值进行比较, 门槛值表达式[14]为:
式中, 和是材料常数; 是有效孪晶分数, 在每个增量步中, 如果最活跃的孪晶系的累计孪晶分数超过, 整个晶粒就根据该孪晶系的取向进行旋转, 这时和得到更新. 目前, VPSC模型已被广泛应用于模拟hcp结构的镁合金在大应变下的力学特征和织构演化[16].
2 结果与分析
2.1 应力-应变曲线
本工作模拟所用的多晶体包括500个晶粒, 初始织构为大部分(0002)面平行于挤压方向的丝织构, 晶粒的形状在每个分析步结束后更新. 变形机制考虑了4种滑移和2种孪生(表1), 结合ZK60镁合金室温轴向拉伸和压缩应力应变实验数据, 通过数值模拟拟合得到材料硬化参数, 列于表1中.
表1 298K下用于黏塑性自洽(VPSC)模拟的ZK60镁合金材料硬化参数
Table 1 Hardening parameters of ZK60 used for viscoplastic self-consistent (VPSC) simulation at 298 K
| Deformation mode | Crystallographic type | τ0 / MPa | τ1 / MPa | θ0 / MPa | θ1 / MPa |
|---|---|---|---|---|---|
| Basal <a> | 5 | 20 | 450 | 0 | |
| Prismatic <a> | 185 | 80 | 300 | 0 | |
| Pyramidal <a> | 310 | 150 | 800 | 0 | |
| Pyramidal <c+a> | 205 | 300 | 4200 | 0 | |
| Tensile twin | 85 | 0 | 0 | 330 | |
| Compressive twin | 272 | 0 | 0 | 90 |
图2所示为ZK60镁合金室温轴向拉伸和压缩真实应力-应变曲线实验与模拟结果, 表2所示为实验得到的拉伸与压缩屈服强度和极限强度. 可见, 拟合曲线与实验数据吻合较好. 挤压态ZK60镁合金室温轴向拉伸和压缩过程中存在明显的不对称性, 主要表现在2个方面: (1) 屈服强度不对称, 拉伸屈服强度约为压缩屈服强度的2.3倍; (2) 应变硬化率不对称, 拉伸时曲线变化较平缓, 而压缩时应变硬化率波动较大.
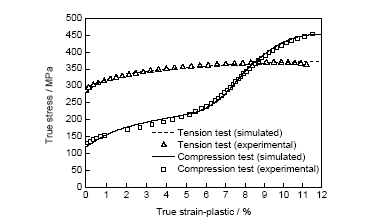
图2 ZK60室温轴向拉伸和压缩真应力-真应变曲线
Fig.2 True stress-true strain curves of ZK60 magnesium alloy under uniaxial tensile and compression
表2 ZK60合金室温轴向拉伸/压缩屈服强度和极限强度
Table 2 Yield strength σs and ultimate strength σb of ZK60 magnesium alloy under uniaxial tensile and compression
| Loading mode | σs / MPa | σb / MPa |
|---|---|---|
| Axial tension | 287 | 369 |
| Axial compression | 125 | 459 |
2.2 极图分析
图3所示为ZK60镁合金初始极图及在不同应变下轴向拉伸和压缩的(0002)和模拟极图. 从图3a可以看出, 初始织构为典型的丝织构, 即大多数(0002)面平行于挤压方向. 由图3b可知, 在拉伸变形初期, (0002)基面向平行于挤压轴方向的集中度不断增加, 塑性应变达到约1%时集中度即达到最大值. 随着应变继续增加(图3c和d), (0002)和极图的类型和集中度基本保持不变, 仍为丝织构状态.
从图3e~g可以看出, 轴向压缩过程中晶粒发生了大角度转动, (0002)基面不断向与挤压轴近似垂直的方向大角度旋转. 当塑性应变达到8%时, 几乎所有晶粒的(0002)基面与挤压轴方向近似垂直. 从图3g和h可以看出, 随着应变的增加, (0002)基面向垂直于挤压方向的集中度不断增强, 应变达到11%左右时集中度达到最大值.
总体而言, 轴向拉伸时晶粒保持基面丝织构形式, 晶粒的取向变化不大; 轴向压缩过程中, 晶粒的取向发生了较大的转变, 晶体的(0002)基面旋转到了与挤压轴近似垂直的方向. 拉伸,压缩变形过程中, 不同的变形机制导致了晶体取向发生相对应的变化, 进而影响拉伸和压缩变形力学行为.
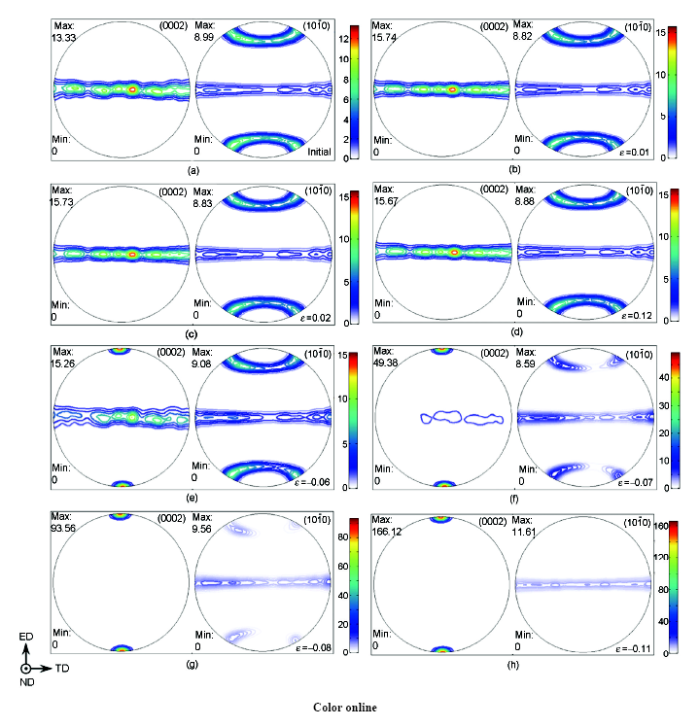
图3 挤压态ZK60镁合金初始极图及轴向拉,压过程中不同应变下(0002)和模拟极图的演变
Fig.3 Simulated (0002) and pole figures of ZK60 alloy of initial texture (a), under uniaxial tensile (b~d) and compression (e~h) under different strains ε (The color scales indicate the pole figure density, ND--normal direction)
2.3 变形机制分析
图4所示为室温拉伸和压缩变形过程中随塑性应变增加各变形机制相对活动量的变化. 由图4a可知, 在轴向拉伸初期(塑性应变小于0.01), 变形机制以基面滑移为主, 柱面滑移为辅. 有研究表明, Mg及其合金室温下基面滑移[17,18]的CRSS约为0.45~0.81 MPa, 柱面<a>滑移[19]约为39.2 MPa, 锥面<c+a>滑移[20]为45~81 MPa, 所以基面滑移最容易启动, 柱面<a>滑移和锥面<c+a>滑移则较难启动. 塑性变形过程中, 各变形机制是否激活取决于外力在滑移面沿滑移方向的分切应力是否达到相应CRSS, 根据分切应力公式:
式中, F/A为宏观真实屈服强度; cos?cosλ为取向因子或Schmid因子; ?为滑移面法向与应力轴的夹角; λ为滑移方向与应力轴的夹角. 由图1a可知, 在挤压丝织构状态下, 大多数晶粒的{0002}基面趋向于平行挤压方向(ED)[8], 基面滑移Schmid因子接近于0, 处于硬取向状态, 只有F/A达到一定高值时, 基面滑移才开始激活, 导致轴向拉伸时具有较高的屈服强度(约为287 MPa). 当塑性应变达到1%时(图4a), 绝大部分晶粒{0002}基面已基本平行于挤压轴, 基面滑移被抑制. 同时, 对于轴比为1.624 (<)的镁合金, 当沿挤压轴方向拉伸时, c轴处于压应力状态, 室温下CRSS较低的拉伸孪生不能启动, 而室温下压缩孪生CRSS又较高, 约为76~153 MPa[21], 也很难启动(图4a). 因此, 随着应变增加, 应力不断升高, 非基面滑移分切应力逐渐达到相应CRSS, 主要变形机制由基面滑移逐渐转变为柱面<a>滑移和锥面<c+a>滑移, 这与Agnew等[22]的研究结果一致. 随着应力逐渐增加, 越来越多的晶粒产生非基面滑移, 硬化率逐渐降低, 直至在原始粗大孪晶界上萌生裂纹并扩展, 最终导致拉伸断裂. 如图5a所示, 从轴向拉伸断口附近纵切面显微组织照片中可观察到粗大孪晶界上存在细小再结晶晶粒, 可判断该孪晶为初始组织中的孪晶. 在室温拉伸过程中, 变形机制以滑移为主, 而孪生较少激活, 这与图4a中的计算结果相吻合. 另一方面, 在本研究中, 锥面<a>滑移在拉伸和压缩变形计算过程中都未显著激活, 因此锥面<a>滑移的影响不再讨论.
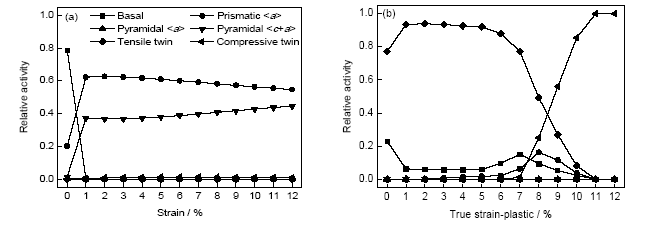
图4 ZK60镁合金在拉伸和压缩变形过程中各种变形机制的相对活动量
Fig.4 Relative activities of different slip and twinning systems during uniaxial tension (a) and compression (b) of ZK60 megnesium alloy with extruded texture
从图4b可以看出, 轴向压缩时基面滑移仍处于硬取向状态而难以激活, 而c轴处于拉应力状态, 且室温下拉伸孪生CRSS较小, 约为2~2.8 MPa[21], 当轴向应力达到125 MPa左右时, 拉伸孪生即开始显著激活, 导致轴向压缩屈服应力明显低于轴向拉伸屈服应力(287 MPa). 需要指出的是, 表1中所列VPSC模型硬化参数由实验数据拟合所得, 各变形机制的CRSS值都是相对大小[16], 其数值同时受到晶粒大小,晶粒形状,固溶体,缺陷结构等多种因素的影响[23], 因此, 不同学者在VPSC模拟过程中使用的CRSS值各不相同, 如Ma等[24]利用VPSC模型对热挤压态AM30镁合金室温轴向与径向压缩行为进行了模拟, 得到室温下拉伸孪生的CRSS为65 MPa, Agnew等[22]对AZ31镁合金力学行为进行了模拟, 得到的拉伸孪生的CRSS为30 MPa, 而本工作得到的拉伸孪生的CRSS为85 MPa. 轴向压缩变形前期, 拉伸孪生为主要变形机制, 相对活动量占到了90%左右, 应力-应变曲线也以较平稳的硬化率逐渐上升(图2). 从图2中还可看到, 塑性应变低于6%, 应力-应变曲线都基本呈线性变化, 应变超过6%以后硬化率迅速上升. 导致硬化率快速上升的原因可能有以下2种: (1) 由图4b可以看出, 当应变达到约6%时, 拉伸孪生的相对活动量开始显著降低, 而此时大量晶粒的(0002)基面已经旋转到了与挤压轴近似垂直的方向(图3e), 这部分晶粒的拉伸孪生受到抑制, 滑移系仍处于硬取向, 很难启动, 室温下压缩孪生的CRSS又很高, 因此可开动的孪生和滑移系很少, 导致应变硬化率迅速上升. 这与Barnett等[25]和Knezevic等[26]的研究结果一致; (2) 由图4b可知, 当应变达到约6%以后, 滑移系的活动量小幅度上升, 这些位错在前期产生的大量孪晶界上堆积, 使得位错滑移受阻, 位错与孪生的这种交互作用宏观上表现为应变硬化率迅速上升. 不过, 压缩变形在达到6%以后, 滑移系活动量虽然升高, 但只是小幅度上升, 位错滑移仍然很少, 因此第一种原因应该是主导因素. 随着应变的增加, (0002)基面向与挤压轴垂直方向的集中度不断增强, 部分基面与挤压轴完全垂直, 有助于压缩孪生的启动, 当应变约为7%时, 分切应力达到压缩孪生的CRSS, 压缩孪生启动. 从图4b可以看到, 在压缩变形后期拉伸孪生相对活动量迅速降低, Ma等[24]在研究热挤压态AM30镁合金室温轴向压缩行为过程中发现, 在变形后期, 拉伸孪生的活动量迅速降低, 体积逐渐减少, 甚至消失, He等[27]在研究挤压态AZ31室温压缩过程中也观察到了此现象. Wang等[28]研究表明, 孪晶可通过孪生与位错的交互运动而不断的变宽, Ma等[24]认为, 轴向压缩变形后期是拉伸孪晶长大与合并的过程, 拉伸孪晶的长大使得基体的体积逐渐缩小, 最终所有的基体被拉伸孪晶所消耗, 只剩下孪晶, 就产生拉伸孪晶消失的假象, 这也证明了图3g模拟结果的正确性. 随着应力的升高, 压缩孪生的活动量迅速上升, 当应变达到约9%时, 压缩孪生成为主导变形机制, 硬化率逐渐降低. 从图2中可以看到, 当应变达到约10%时, 硬化率开始显著下降, 这是因为压缩孪生的大量激活使得塑性变形中积累的应力得到释放的结果[21]. 当应变达到约11%时, 根据图3h所示, (0002)基面向与挤压轴垂直方向转动的集中度达到最大值, 此时(0002)基面几乎完全与挤压轴垂直, 拉伸孪生和滑移系启动受到抑制, 压缩孪生相对活动量达到最大值(接近1). 由图5b可见, 在轴向压缩后期, 合金中产生了大量细长的带状孪晶, 可判断为压缩孪晶[29], He等[27]通过研究挤压态AZ31镁合金室温轴向压缩过程, 也发现了在压缩变形后期至断裂的时候合金中产生了压缩孪晶, 从而验证了模拟结果的可靠性.

图5 ZK60 镁合金拉伸和压缩断裂面附近纵切面显微组织
Fig.5 Morphologies of longitudinal section near the failure surface of the extruded ZK60 magnesium alloy after tension
(a) and compression (b) to fracture
3 结论
(1) 通过修正黏塑性自洽模型, 建立了耦合滑移和孪生的晶体塑性力学模型. 对挤压态ZK60镁合金室温轴向拉伸和压缩实验进行了数值模拟, 从微观变形机制的角度分析了具有初始挤压态丝织构镁合金拉-压不对称性产生的机理. 所建立的模型能够很好地模拟镁合金塑性变形过程, 模拟结果与实验结果吻合较好.
(2) 基面滑移在轴向拉伸初期相对活动量很高, 但此时其取向因子较低, 处于硬取向, 导致轴向拉伸屈服应力较高; 随着晶粒转动, 基面滑移分切应力降低, 变形机制转为以柱面滑移为主, 辅以锥面<c+a>滑移, 应变硬化率较低, 应力-应变曲线较平稳.
(3) 轴向压缩前期, 临界剪切应力较低的拉伸孪生大量激活, 导致屈服应力较低; 应变达到约6%时拉伸孪生相对活动量迅速降低, 同时滑移和压缩孪生很难激活, 导致应变硬化率迅速上升. 当应变达到约10%时, 压缩孪生大量激活使得塑性变形积累的应力得到释放, 硬化率降低. 因此, 在压缩变形中, 孪生相对活动量对应变硬化率有着重要影响.
(4) 挤压丝织构状态决定了镁合金在室温轴向拉-压变形过程中变形机制存在明显区别, 从而导致挤压镁合金产生显著的轴向拉-压不对称性.
来源--金属学报






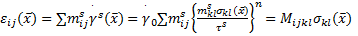
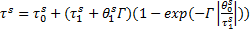
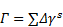
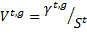
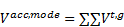
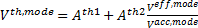
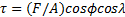

 沪公网安备31011202020290号
沪公网安备31011202020290号
