分享:一种基于黏弹性理论预测DP600钢板滞后回弹的新模型
北京理工大学材料学院, 北京 100081
摘要
通过加载不同预应变和保压时间获得了DP600钢板的室温滞后回弹响应. 基于黏弹性理论, 采用309 MPa恒应力室温蠕变实验, 获得了预测滞后回弹过程的蠕变柔量函数. 基于DP600钢板室温弹性和塑性加载响应, 修正了线黏弹性本构方程的积分下限, 将柔量函数与修正的应力率函数进行卷积, 获得了影响滞后回弹过程的加载历史效应. 再将加载历史应变波形与卸载脉冲叠加, 获得不同预变形量的滞后回弹应变预测值. 结果表明, 滞后回弹初期应变率较高, 之后应变率逐渐降低; 随着预应变的增加, 滞后回弹应变的绝对值逐渐递增, 并且滞后回弹占总回弹比例逐渐增加; 滞后回弹预测方向与瞬时回弹方向相同, 与加载方向相反; 相同时间段内, 蠕变回弹应变比滞后回弹应变明显降低, 与滞后回弹实验相比, 蠕变恒应力与蠕变回弹应变的比值随预应变的变化规律呈现出良好的线性关系; 基于黏弹性理论的修正模型所得到的预测值接近实验测量值, 并能够较好地反映实验变化规律.
关键词:
随着汽车、航空航天制造技术不断向高精度、轻量化方向发展, 各种新型高强度钢板和镁合金、铝合金等轻合金板材的应用越来越广泛, 因而对它们的成形性特别是成形后形状稳定性的研究愈发重要. 回弹是影响金属塑性成形后形状稳定性的最主要因素, 实际上, 很多金属板材或管材在塑性成形后会经历2种回弹: 一种是卸载瞬间时刻发生的瞬时回弹[1-4]; 另一种是随着时间的推移, 其形状尺寸在卸载后还将继续发生微小的变化, 称其为“滞后回弹”或“时间依赖性回弹”[5-8]. 近年来, 关于金属变形回弹的研究取得了一些进展, 但关于滞后回弹现象的发生和发展还鲜为人知, 而回弹的滞后性作为潜在因素将直接影响零部件的装配精度, 需引起足够的重视.
对时间依赖性行为的研究始于20世纪40年代. Zener[9]首次定义并明确了金属黏弹性(viscoelasticity)和滞弹性(anelasticity)的区别. 1972年, Nowick[10]提出, 应将金属的黏弹性与内耗相区分. 滞后回弹的微观机理与点缺陷、线缺陷以及面缺陷的运动和相互作用有关[11,12]. 目前, 室温下自然状态的金属滞后回弹行为的常见激发方式为塑性变形及之后的瞬时卸载联合作用, 因而塑性变形的微观机理与滞后回弹的微观机理有着密切的联系. 同时, 滞后回弹的激发方式与蠕变回弹基本相同, 蠕变回弹也可看成滞后回弹的特殊情形.
Wang等[13]和Lim等[14]研究了几种高强钢以及铝合金板材的单向拉伸滞后回弹以及拉弯滞后回弹, 通过调节弯曲半径及拉应力等工艺参数, 改变弯曲角的滞后回弹量, 认为在卸载后2 h内, 主要为黏弹性机理控制. 然而目前, 专门针对室温滞后回弹的预测模型还极少, 黏弹性理论的应用还主要针对于实验结果的被动拟合上.
Wang等[13]采用室温蠕变模型对室温滞后回弹进行模拟, 结果表明其滞后回弹量的准确性强烈地依赖于变形卸载之后的残余应力场. 而线黏弹性理论以蠕变和Boltzmann叠加原理为基础, 通过卷积计入历史效应对后期应变或应力的影响, 并且进一步计入其他非线性效应的修正也更加灵活[15]. 因而亟待开发基于黏弹性理论, 能够反映不同加载历史效应的滞后回弹预测模型. 预测金属滞后回弹的模型主要涉及2个方面: 一是对滞后回弹趋于平衡时的滞后回弹应变的预测; 二是对滞后回弹特征时间的预测, 例如弛豫时间.
单向拉伸实验有清晰的应力-应变对应关系, 便于研究滞后回弹规律, 同时也是研究多向应力状态下应变响应的重要基础. 然而目前, 对室温拉伸滞后回弹实验现象的研究还不够充分. 为了揭示不同的加载历史对DP600钢板滞后回弹的影响规律, 针对DP600钢板进行了单向拉伸和室温蠕变实验, 采用不同的加载预应变, 测试卸载后的室温滞后回弹响应, 提出了一种基于黏弹性理论的弹性后效修正公式, 重点预测DP600钢板室温滞后回弹应变.
1 实验方法
实验所用DP600钢板的主要化学成分(质量分数, %)为: C 0.009, Si 0.36, Mn 1.84, S 0.005, Al 0.05, Fe余量. 采用WDS-10T万能电子试验机进行室温滞后回弹和蠕变实验. 试样取样方向平行于轧制方向, 平行段长度70 mm, 标距长度50 mm, 宽度15 mm, 厚度1.6 mm. 引伸计分辨率为0.001 mm.
拉伸预应变为0.06%, 0.2%, 5%, 8%, 10%和15%的试样编号分别为EI-0.06, PI-0.2, PI-5, PI-8, PI-10和PI-15, 其中首字母E代表弹性加载, P代表塑性加载; 第2个字母若为I代表直接卸载的滞后回弹实验, 数字代表拉伸预应变; 若第2个字母为C代表蠕变实验, 数字代表蠕变过程的预应变. 蠕变恒应力取应力-应变曲线上预应变对应的应力. 对于DP600钢板宏观屈服应力以下PC-0.2, PC-0.3, PC-0.33和PC-0.4试样的蠕变实验采用恒载荷率500 N/s快速加载, 滞后回弹实验采用恒位移率1 mm/min方式加载, 各实验忽略弹性加载和蠕变过程的试样横截面尺寸变化, 以恒应力率和恒应力进行分析.
加载过程的数据采集方式采用实验设备既定采集频率1.85 s-1. 加载至预应变后, 立即卸载. 当试样与下夹头完全脱离时(卸载后20 s之内), 记录引伸计所示位移作为滞后回弹初始位移. 滞后回弹和蠕变回弹实验采用非等时间间隔采集数据, 以便完整记录数据变化细节. 具体方法如下: 在每次示数发生变化时, 若示数变化后稳定, 记录稳定值和变化瞬时时刻; 若示数波动, 取波动值的平均值, 并记录其瞬时时刻. 而滞后回弹和蠕变实验的加载阶段, 仍按实验设备设定的等时间间隔采集数据.
2 实验结果与讨论
2.1 单向拉伸实验
图1为DP600钢板单向拉伸实验的应力-应变曲线. 通过应力-应变曲线获得的DP600钢板的基本力学性能如下: 弹性模量为182 GPa, 屈服强度为345 MPa, 抗拉强度为628 MPa, 屈强比为0.549, 最大应力塑性延伸率为22.17%, 强度系数为1062.9, 加工硬化指数为0.207. 由于实际生产中, 板料拉深变形基本处于均匀塑性变形区, 因而将均匀塑性变形区作为研究重点.
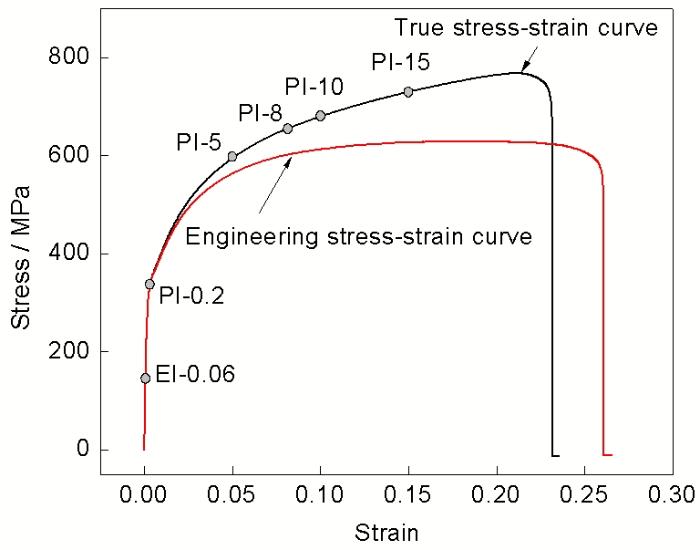
图1 DP600钢板单向拉伸应力-应变曲线
Fig.1 Stress-strain curves in uniaxial tensile test for DP600 steel sheet
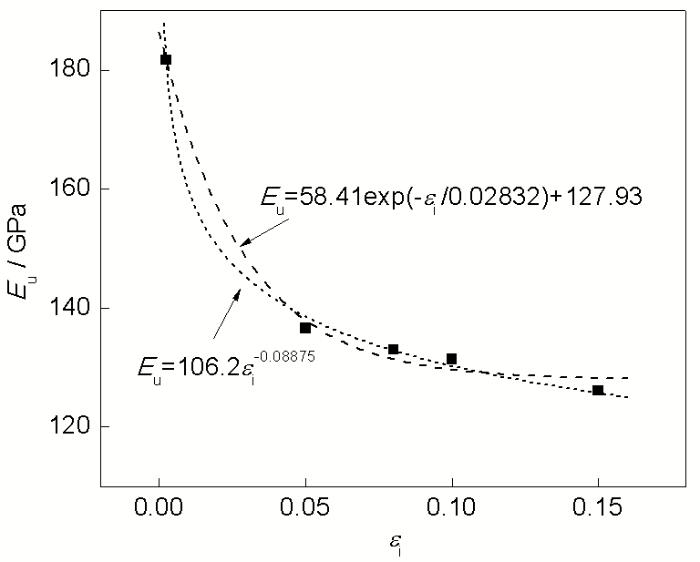
图2 滞后回弹瞬时模量Eu-预应变ei曲线
Fig.2 Eu varied with pre-strain εi under strain e=1.7×10-4
2.2 瞬时回弹
表1为EI-0.06, PI-0.2, PI-5, PI-8, PI-10和PI-15试样直接卸载后的瞬时回弹与滞后回弹数据. 可知, 随着预应变的提高, 卸载应力si增大, 同时瞬时回弹应变Δeis也增大. 定义si与Δeis的比值为滞后回弹瞬时模量Eu, 其物理含义为单位瞬时回弹应变所对应的卸载应力; si与滞后回弹应变Δer的比值为滞后回弹模量Ei, 其物理含义为单位滞后回弹应变所对应的卸载应力:
表1 试样经直接卸载后的瞬时回弹与滞后回弹
Table1 Initial springback and time-dependent springback without holding time
| Specimen | si / MPa | Δeis | Eu / GPa | Δer | Ei / GPa | etol | p / % |
|---|---|---|---|---|---|---|---|
| EI-0.06 | 116 | -0.00060 | 193.3 | - | - | -0.00060 | - |
| PI-0.2 | 309 | -0.00164 | 188.4 | -0.00006 | 5150 | -0.00170 | 3.53 |
| PI-5 | 593 | -0.00434 | 136.6 | -0.00020 | 2965 | -0.00454 | 4.41 |
| PI-8 | 653 | -0.00496 | 131.7 | -0.00028 | 2340 | -0.00524 | 5.32 |
| PI-10 | 678 | -0.00516 | 131.4 | -0.00030 | 2260 | -0.00546 | 5.49 |
| PI-15 | 729 | -0.00578 | 126.1 | -0.00042 | 1735 | -0.00620 | 6.77 |
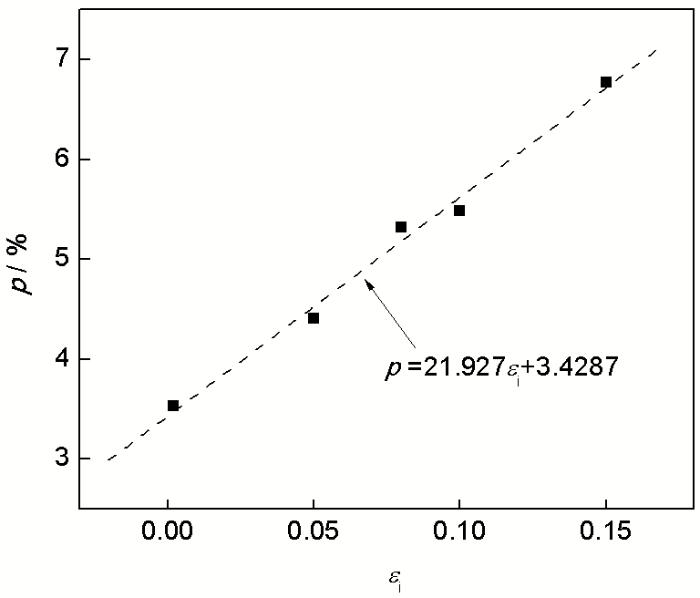
图3 滞后回弹占比p与ei关系曲线
Fig.3 Measured p as a function of ei
将表1的Eu数据绘于图2. 可知, Eu随预应变ei的提高而单调递减, 呈现滞后回弹瞬时模量软化现象[14,16] . 由于DP600钢板的Eu呈现指数衰减趋势, 因而对图2中数据, 分别采用指数与幂函数进行拟合, 结果为:
2.3 滞后回弹
从表1中可见, 对于弹性加载实验, 试样EI-0.06卸载后, DP600钢板的瞬时回弹应变等于其加载应变, 并且其滞后回弹量微小, 低于引伸计的分辨率, 说明室温下DP600钢板在弹性应力卸载后, 滞后回弹十分微弱. 当预应变ei增至0.2%时, PI-0.2试样的Δer的绝对值仅为0.006%, 仍十分微小. 表1中数据的负号, 代表与预应变的方向相反. 当ei达到5%时, DP600钢板经历了一定的塑性变形后, PI-5试样的Δer的绝对值达到0.02%, 比PI-0.2试样提高了近一个数量级, 滞后回弹现象较为明显. 随着ei的继续提高, Δer的绝对值也逐渐增大. 当ei为15%时, DP600钢板Δer的绝对值达到最高值0.042%, 比PI-5试样提高了一倍多. 定义Δer占总回弹(Δeis+Δer)的比例为滞后回弹占比p, 有:
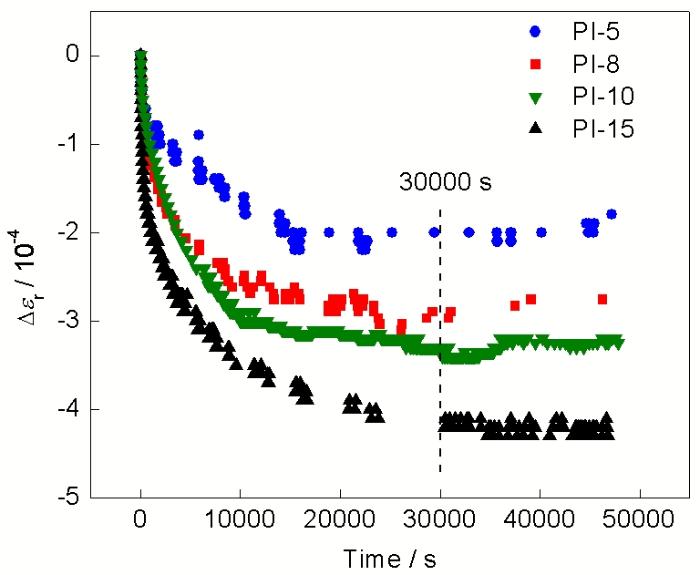
图4 滞后回弹应变Δer与时间的关系曲线
Fig.4 Measured time-dependent springback strain Δer varied with time
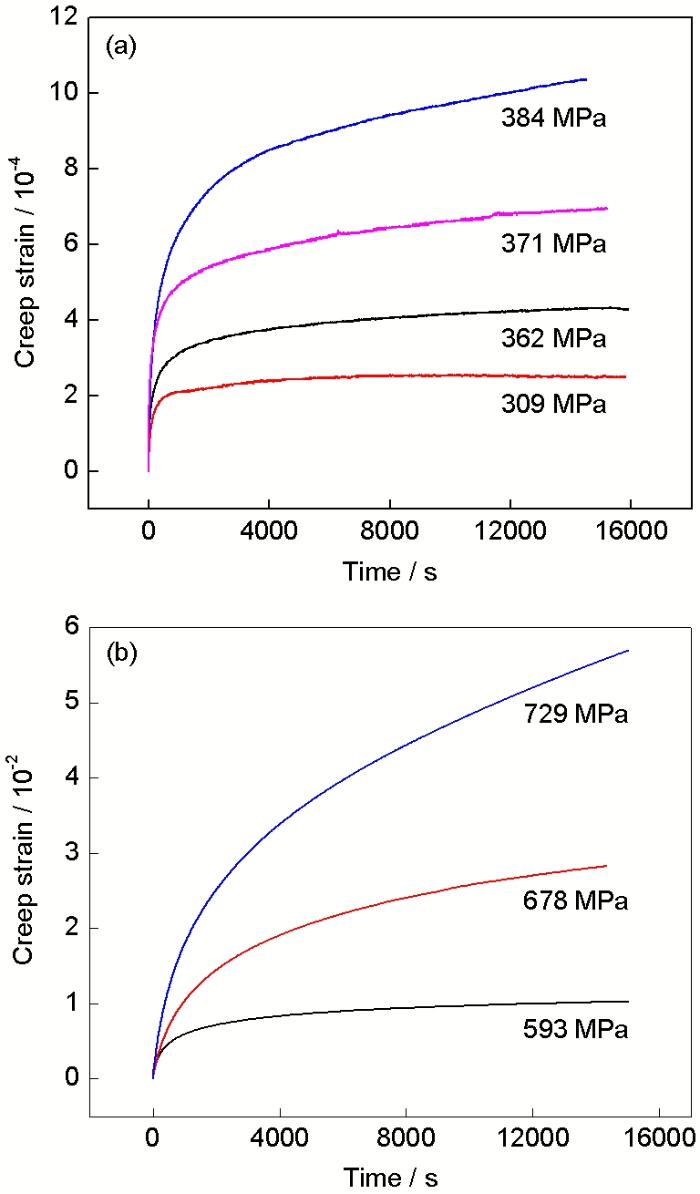
图5 DP600钢板在较低和较高恒应力下保压4 h的蠕变曲线
Fig.5 Creep curves of DP600 steel sheet under low (a) and high (b) stresses holding for 4 h
图3为DP600钢板p与ei的关系. 由图3可知, p随着ei的提高而增大, p由PI-0.2试样的3.53%增加到PI-15试样的6.77%, 其变化规律接近线性分布. 对其进行线性拟合为:
图4为PI-5, PI-8, PI-10和PI-15试样卸载后15 h内的Δer与时间的关系曲线. 由图4可知, 试样的Δer随时间增长呈现指数衰减. 在滞后回弹初期, 应变回弹速率较高, 随着时间的推移, 应变回弹速率逐渐降低. PI-5试样滞后回弹的弛豫饱和时间约为15000 s. 弛豫饱和时间随着ei的增加而逐渐增加, 各曲线基本达到回弹饱和时, 饱和弛豫时间约为30000 s.
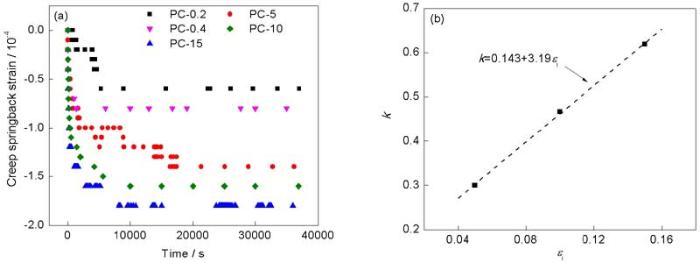
图6 DP600钢板蠕变保压4 h的蠕变回弹应变和蠕变回弹降幅占比k
Fig.6 Creep springback strain of DP600 steel sheet (a) and loss percentage k for creep springback (b)
2.4 室温蠕变与蠕变回弹
金属室温下的蠕变响应取决于金属内部组织成分与外部载荷条件. 室温蠕变可以理解为时间依赖性的塑性行为, 并且通常在低于宏观屈服应力Rp0.2下即可进行[17-20]. DP600钢板室温蠕变实验的目的有2个: 一是获得不同应力水平下材料的室温蠕变规律, 以获得黏弹性模型中的柔量函数构建预测模型[21]; 二是获得室温蠕变回弹随预应变的变化规律.
为获得蠕变柔量函数, 在较低应力下进行了不同恒应力蠕变实验. 恒应力分别为309, 362, 371和384 MPa, 其在图1中的真应力-应变曲线上, 分别对应应变0.20%, 0.29%, 0.35%和0.41%. DP600钢板在上述较低应力下保压4 h的室温蠕变曲线如图5a所示. 可见, 随着恒应力水平的提高, 蠕变应变逐渐升高. 各条曲线在流变初期即蠕变第一阶段, 应变增长较快, 应变率较高, 之后随时间的延长逐渐降低, 在保压4 h结束时应变率依次为0, 2.7×10-9, 5.1×10-9和1.4×10-8 s-1. 可见, 309 MPa下的蠕变应变在4 h内基本达到饱和, 这与蠕变柔量函数的变化规律比较符合. 同时, 蠕变应变的数量级与DP600滞后回弹应变均为10-4, 因而选取309 MPa下的蠕变曲线进行拟合, 以获得蠕变柔量. DP600钢板在较高应力下保压4 h的室温蠕变曲线如图5b所示. 恒应力选取图1中应变5%, 10%和15%所对应的真应力593, 678和729 MPa. 可见, 随着恒应力水平的提高, 蠕变应变也逐渐升高, 并且明显高于低应力水平下的蠕变应变. 在较高应力水平下蠕变实验保压4 h结束时的应变率依次为9.7×10-8, 5.8×10-7和1.6×10-6 s-1.
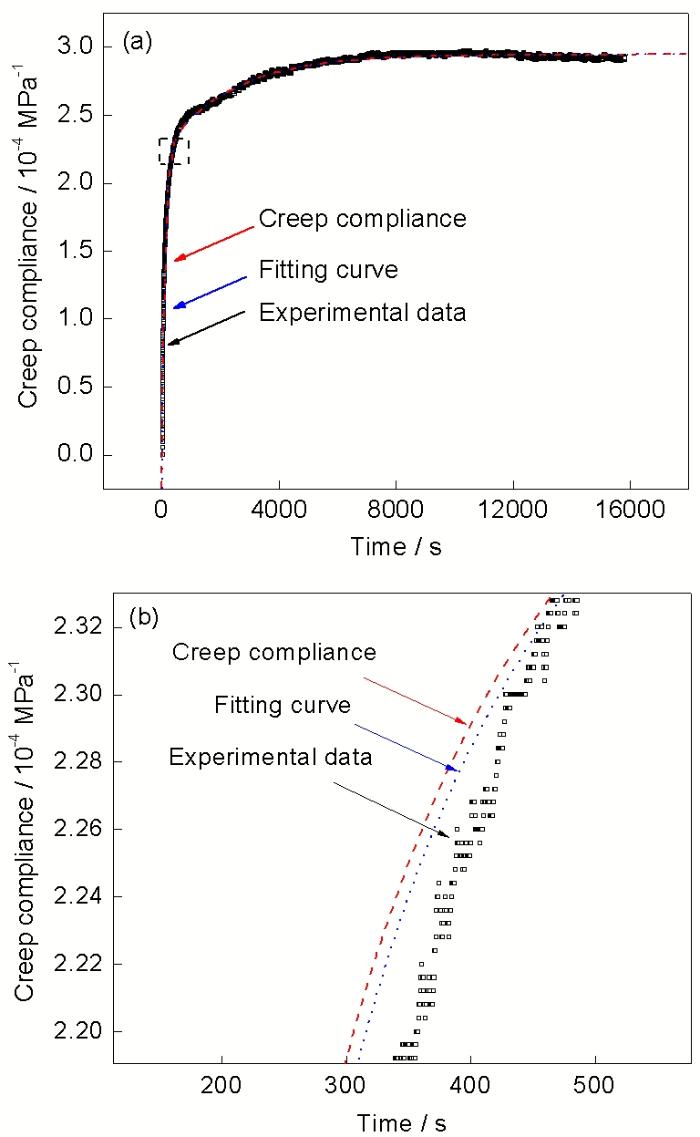
图7 DP600钢板柔量函数拟合及局部放大图
Fig.7 Fitting curve of creep compliance for DP600 (a) and detail view of marked area in Fig.7a (b)
表2 蠕变保压4 h后的蠕变瞬时回弹与蠕变回弹
Table 2 Initial springback for creep and creep springback after holding for 4 h
| Specimen | sic / MPa | Δeisc | Euc / GPa | Δerc | Eic / GPa | etol | v / % |
|---|---|---|---|---|---|---|---|
| PC-0.2 | 309 | -0.00178 | 167.4 | -0.00006 | 5150 | -0.00184 | 3.26 |
| PC-0.3 | 362 | -0.00216 | 166.6 | -0.00008 | 4525 | -0.00224 | 3.57 |
| PC-0.33 | 371 | -0.00224 | 165.1 | -0.00008 | 4637 | -0.00232 | 3.44 |
| PC-0.4 | 384 | -0.00232 | 163.7 | -0.00008 | 4800 | -0.00240 | 3.33 |
| PC-5 | 593 | -0.00446 | 132.9 | -0.00014 | 4235 | -0.00460 | 3.04 |
| PC-10 | 678 | -0.00544 | 124.6 | -0.00016 | 4237 | -0.00529 | 2.83 |
| PC-15 | 729 | -0.00618 | 117.9 | -0.00018 | 4050 | -0.00636 | 2.83 |
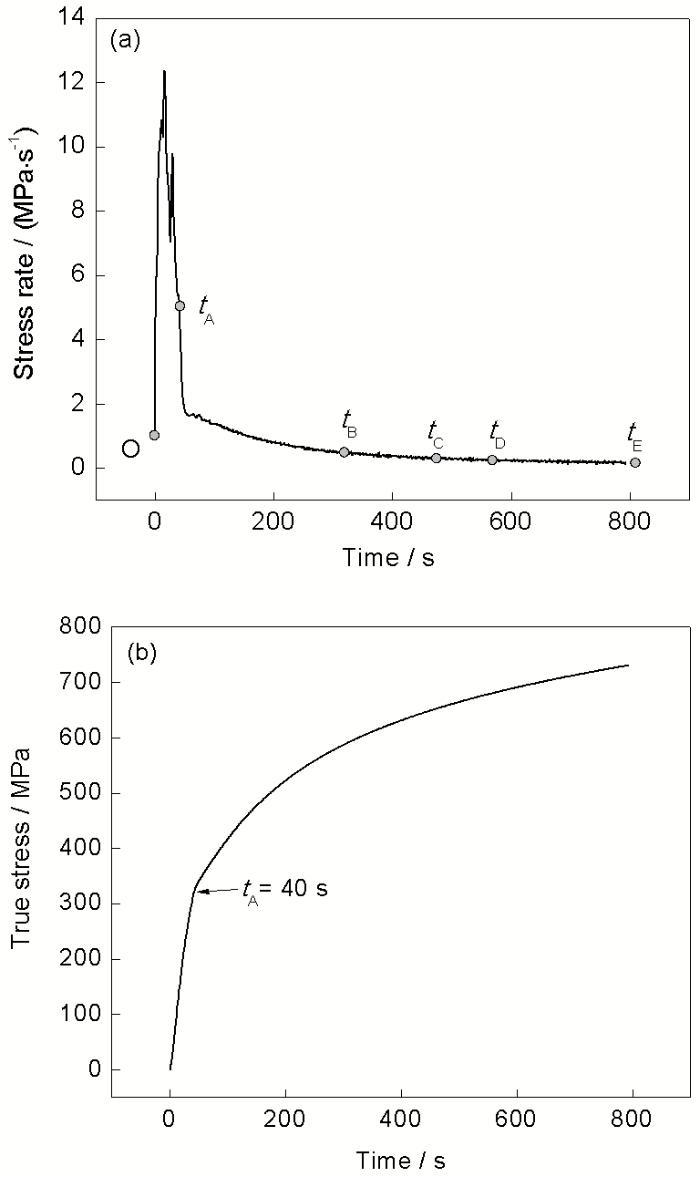
图8 应力率-时间曲线和应力-时间曲线
Fig.8 Stress rate-time curve (a) and stress-time curve (b) (tA is the starting point of stress rate function; tB, tC, tD and tE are the times of unloading for specimens PI-5, PI-8, PI-10 and PI-15)
图6a为DP600钢板在不同恒应力下的蠕变回弹曲线, 并将相关实验结果列于表2中. 可见, 随着蠕变恒应力sic的逐渐增大, 相同回弹时间内的蠕变瞬时回弹应变Δeisc和蠕变回弹应变Δerc的绝对值也逐渐增大. 定义sic与Δeisc的比值为蠕变回弹瞬时模量Euc, 其物理含义为单位瞬时回弹应变所对应的卸载应力; 而sic与Δerc的比值为蠕变回弹模量Eic, 其物理含义为单位蠕变回弹应变所对应的卸载应力; 定义Δerc占总回弹(Δeisc+Δerc)的比例为蠕变回弹占比ν. PC-0.3, PC-0.33, PC-0.4, PC-5, PC-10和PC-15试样的Euc与滞后回弹实验的Eu类似, 随着应力的提高, 逐渐降低; 而Eic与滞后回弹实验的Ei相比, 随着卸载应力的提高呈现良好的稳定性; 而ν与p相比, 随着卸载应力的提高略有降低, 整体变化较为稳定, 因而Eic和ν均呈现了一定的稳定性. 由图6a中的PI-5, PI-10和PI-15以及图4中的PC-5, PC-10和PC-15试样的实验曲线比较可知, 经过4 h的保压过程, Δerc的绝对值与Δer的绝对值相比明显降低. 将PC-5, PC-10和PC-15试样的Δerc以PI-5, PI-10和PI-15试样的Δer为标准, 定义蠕变回弹降幅占比k为Δerc的减少量与Δer的比值:
k与ei的关系如图6b所示. 可见, k与ei呈现良好的线性关系, 线性拟合结果为:
2.5 蠕变柔量
根据黏弹性理论, 蠕变柔量J(t)为材料在单位阶跃应力下的应变响应:
式中, s0为所加恒应力, e(t)为材料的应变响应. 由于在实验中不易实现瞬态加载, 不同加载条件下的蠕变实验均具有加载历史, 加载历史将影响黏性材料后续的应变变化[22,23]. 为获得不含有加载历史效应的蠕变柔量, 同时考虑到PC-0.2试样的恒应力率加载, 采用Prony级数的柔量拟合方法进行处理[24-26]. 一维黏弹性积分型本构方程如下[15]:
式中, z为积分变量; J(t-z)为经过时移和反转变换的蠕变柔量函数;
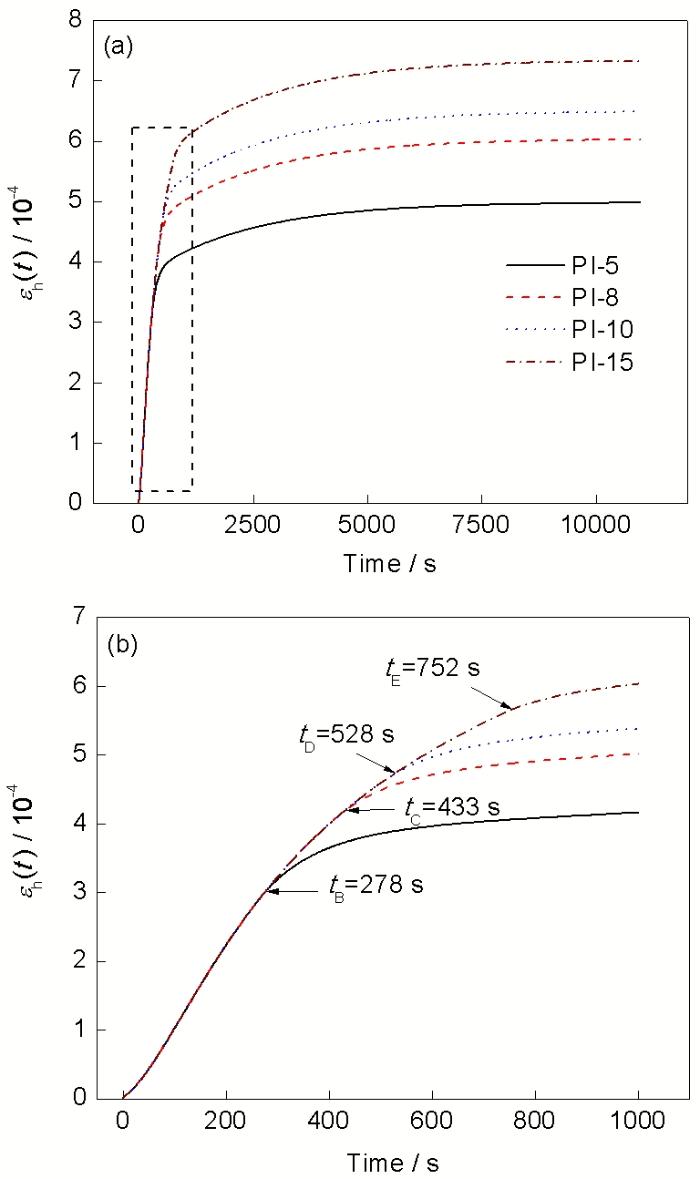
图9 不同预变形量的卷积拟合曲线及局部放大图
Fig.9 Convolutions of historical loading effect under different pre-strains (a) and detail view of marked area in Fig.9a (b)
以卸载时刻t1作为式(11)积分限的分界点, 式(11)可改写为:
注意到:
式(12)可简化为:
对于PC-0.2为恒应力率加载试样,
为了便于分析滞后回弹, 选取无冲击响应的4参数Kelvin链进行分析[15], 柔量函数可表示成:
式中,
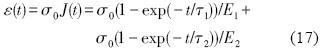
将式(16)代入式(15), 积分得计入恒应力率加载历史影响的应变函数:
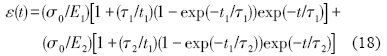
由于PC-0.2试样的t1=20 s, 将其代入式(18). 为简化拟合, 采用下式:
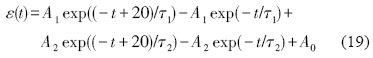
式中, A1和A2为指数项的待定系数, A0为常数项的待定系数. 采用式(19)对PC-0.2试样的蠕变曲线进行拟合, 拟合结果为A0=0.00029, A1=-0.00105, A2=-0.00826,
对比式(18)和(19), 可得:
将相关系数代入式(17), 可得DP600钢板在阶跃应力309 MPa下的应变响应为:
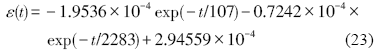
对应的蠕变柔量函数为:
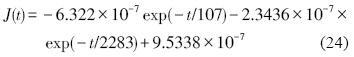
2.6 应力率函数
采用中心差分数值计算方法对实验数据进行处理, 得到的应力率-时间关系曲线如图8a所示, 对应的应力-时间曲线如图8b所示. 由图8a可知, 应力率与时间不再满足线性关系, 所以加载历史效应eh(t)对滞后回弹的影响应由应力率函数与柔量函数卷积而得, 即式(14). 由EI-0.06试样的实验结果可知, 在弹性加载阶段, 室温下DP600钢板的黏性行为十分微弱, 基本无滞后回弹过程. 所以依据图8b所示, 将计入历史效应的应力率起始时刻取为加载后第40 s, 如图8a和b中tA点所示, 对应应变约为0.2%. 对式(14)的积分下限修正为a, 有:
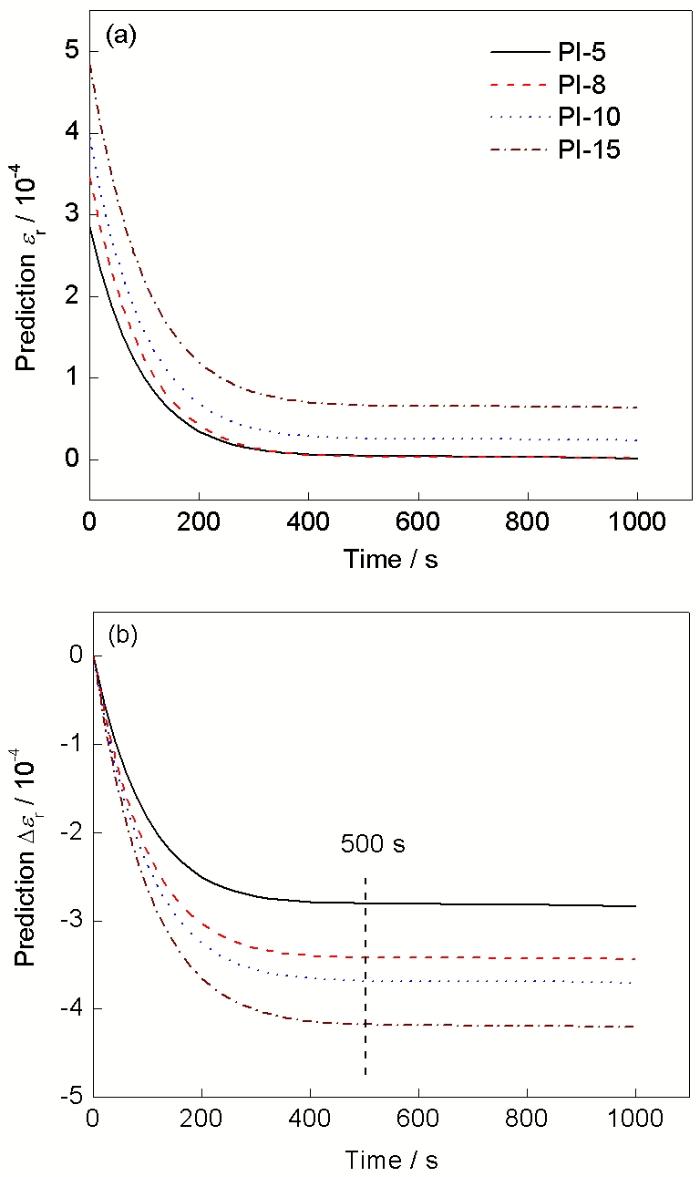
图10 弹性后效应变曲线和滞后回弹应变预测曲线
Fig.10 Elastic after effect strain curves (a) and time-dependent springback strain curves for prediction (b)
PI-5, PI-8, PI-10和 PI-15试样滞后回弹实验卸载时刻分别为tB, tC, tD和tE, 如图8a所示. 因而, 对于PI-5, PI-8, PI-10和PI-15试样滞后回弹实验, 影响滞后回弹过程的应力率时间曲线段分别为tA-tB段、tA-tC段、tA-tD段和tA-tE段.
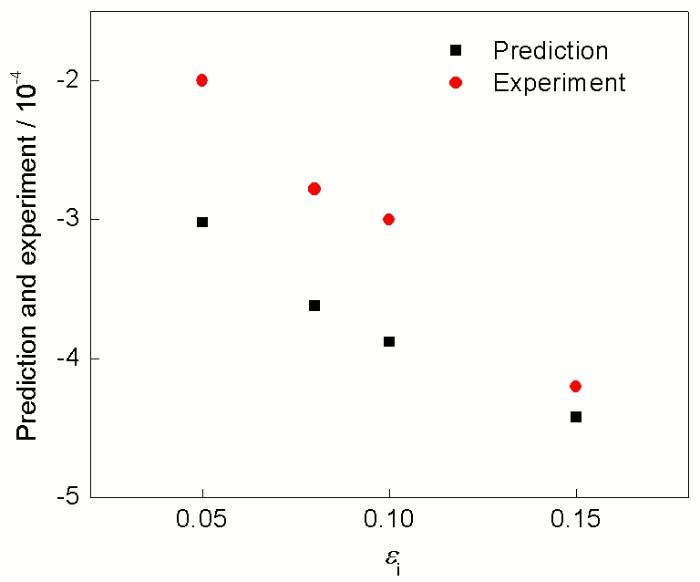
图11 滞后回弹实测应变与预测应变随预应变εi的变化规律
Fig.11 Experimental strain and predicted strain of time-dependent springback varied with pre-strain ei
2.7 不同预应变滞后回弹预测
依据式(25), 通过Matlab数值分析软件计算应力率函数与柔量函数离散序列的卷积和. 通过将卷积和拟合, 获得PI-5, PI-8, PI-10和PI-15试样的加载历史效应曲线eh(t), 如图9a所示, 前1000 s的放大图如图9b所示, 并在图9(b)中标出了PI-5, PI-8, PI-10和PI-15试样对应的卸载时刻tB, tC, tD和tE.
由以上讨论可知, t1在PI-5, PI-8, PI-10和PI-15试样的实验中分别为tB, tC, tD和tE. 根据式(9), 卸载脉冲效应函数-eu(t)可表示为:
式中, si为滞后回弹实验的卸载应力, 式(26)中的负号表示卸载过程的应力增量为负. 由Boltzmann叠加原理, 分别在图9b中所示的tB, tC, tD和tE时刻, 叠加卸载脉冲效应函数-eu(t), 那么弹性后效应变函数er(t)可表示为:
式中, eh(t+t1)为经过时移变换的加载历史效应函数. 将式(25)和(26)代入式(27), 有:
将图9a中的卷积函数和柔量函数式(24)分别代入式(28), 可得PI-5, PI-8, PI-10和PI-15试样的弹性后效应变曲线如图10a所示. 为便于比较不同试样的滞后回弹应变, 将弹性后效应变er(t)减去零时刻的初始应变er(0)可得滞后回弹应变Δer(t)的预测公式, 有:
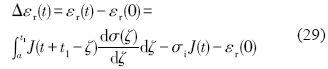
由式(29)所获得的各曲线滞后回弹应变波形如图10b所示. 可知, 式(29)较好地反映了图4中滞后回弹应变的绝对值随着ei增加而递增的趋势. 图11为滞后回弹应变预测值与实验值的比较. 可知, 滞后回弹应变预测值较为接近实验测量值, 并且随着ei的增加均呈现近似线性的变化规律. 各预测曲线基本达到弛豫饱和时, 饱和时间约为500 s, 如图10b所示, 约为图4所示曲线的1/60, 因而弛豫饱和时间的预测可由比值1/60近似估测.
考虑到蠕变保压过程对蠕变回弹的影响, 由式(8)可引入因子(1-k), 与式(29)相乘以使模型计入保压过程的影响, 有:
式中,
3 结论
(1) DP600钢板在滞后回弹实验中, 滞后回弹瞬时模量随着预应变的增加而呈现递减规律. 滞后回弹初期具有较高的回弹驱动力, 应变率较高; 随着时间的推移, 回弹驱动力减小, 应变率逐渐降低; 随着预应变的增加, 滞后回弹占总回弹比例逐渐增加.
(2) DP600钢板在蠕变实验中, 蠕变回弹瞬时模量随着预应变的增加也呈现递减规律. 在相同的回弹时间内, 蠕变回弹应变比直接卸载的滞后回弹应变明显减小; 经过4 h的蠕变保压过程, 蠕变回弹模量随预应变的增大变化较小, 接近线性关系, 而滞后回弹模量的变化规律呈现减小趋势.
(3) 通过对线黏弹性本构方程积分下限的修正, 构建了反映非线性效应的新型滞后回弹预测模型. 滞后回弹的预测方向与实测方向相同, 同时滞后回弹应变的预测值接近实测值; 滞后回弹应变预测值的绝对值随预应变的增加而单调递增, 呈线性分布, 较好地反映了滞后回弹实测应变的变化规律
来源--金属学报






 沪公网安备31011202020290号
沪公网安备31011202020290号
