分享:铁磁性三维Ising模型精确解及时间的自发产生
本文综述在三维Ising模型精确解方面取得的研究进展。首先介绍作者构建的拓扑量子统计物理学,包括时间平均、Jordan-von Neumann-Wigner框架、拓扑结构对热力学性质的贡献等学术思想。然后介绍用Clifford代数方法和Riemann-Hilbert问题的方法证明作者提出的两个猜想,证明在两个猜想基础上推定的三维Ising精确解的正确性。在此基础上,探究了时间的本源,得出三维多体相互作用体系中粒子(自旋)间相互作用自发产生时间的结论。
关键词:
Ising模型是一个非常重要的理论模型,可以用来描述在多体相互作用自旋体系的物理性能和相变过程[1]。Ising模型中的自旋具有2种可能的状态(向上或向下),通常仅考虑自旋之间存在最近邻相互作用。三维Ising模型可以被映射为许多物理模型,应用到物理、化学、生物、数学、计算机、经济、社会等学科领域。例如,Ising模型可以用来描述晶体的磁性、合金中的有序-无序转变、液氦到超流态的转变、液体的冻结和蒸发、晶格气体、玻璃物质的性质、森林火灾、城市交通、蛋白质分子的折叠、计算机的逻辑等。1925年,Ising[1]发表了一维Ising模型的精确解,模型由此命名。1944年,Onsager[2]求出了二维Ising模型自由能和比热容的精确解,被视为统计物理的重大进展。1952年,Yang[3]求出二维Ising模型的自发磁化强度精确解。三维Ising模型精确解是物理学著名的百年难题,由于存在拓扑学问题,许多著名科学家试图求解均未能成功。
2007年,作者[4]提出两个猜想,并且在两个猜想基础上推导出铁磁性三维Ising模型的精确解(张氏猜想)。两个猜想为:猜想一,可以用四维空间的旋转解决三维Ising模型的拓扑学问题;猜想二,在三维Ising模型的本征矢量上存在权重因子代表从四维到三维的投影。论文发表后在国际学术界引起强烈反响和学术争鸣。一些国际著名统计物理学家表示反对,主要认为与前期的高温展开、低温展开不吻合,还认为高温展开应是收敛的[5~10]。作者认为这些近似方法不能作为评价标准,因为这些展开方法没有考虑三维Ising模型的拓扑学问题,必然存在系统误差,而且在无限高温度处没有严格证明高温展开的收敛性[11~13]。一些国际著名物理学家和数学家支持作者的工作[14~19]。
2019年,作者与Suzuki、March[20]发展了一种三维Ising模型的Clifford代数方法。指出求解三维Ising模型的精确解存在三大困难:非局域性、非Gauss性、非对易性。证明了四个定理[20]:迹不变定理、线性化定理、局域变换定理、对易性定理。这四个定理解决了上述三大困难,严格地证明了作者提出的两个猜想,表明在猜想基础上提出的铁磁性三维Ising模型精确解是正确的。2021年,作者与Suzuki[21,22]用Riemann-Hilbert问题的方法再次证明了张氏猜想。通过建立配分函数中拓扑结构与代数的关系,在Riemann面上表示出拓扑结构,用Riemann-Hilbert问题的方法,利用单项(monoidal)变换去除奇异性,将非平庸的拓扑结构平庸化。再定义顶角算子和平坦矢量丛,应用Gauss-Bonnet-Chern定理解释拓扑相因子。
研究[4,11~13,20~22]认为,高温展开、低温展开、Monte Carlo、重整化群理论不是解决上述三大困难的方法,不可能获得精确的结果。尽管高温展开、低温展开等微扰展开方法在二维与Onsager[2]、Yang[3]的精确解一致,但是这些展开方法仅仅考虑自旋周围的局域排列、自旋局域排列的平面图形的周长等,没有考虑三维模型中自旋间长程纠缠、全局性的纽结。Monte Carlo、重整化群理论等计算机模拟方法通常需要构建一个L × L × L (L为大晶胞中一条边上晶格点的数目)大晶胞,应用周期性边界条件在三维空间重复这个大晶胞。由于计算机计算能力的限制通常L小于100。而三维Ising模型中沿着第三维度方向上2个最近邻自旋之间的相互作用涉及到二维平面内n个自旋间的长程量子纠缠(在热力学极限条件下n → ∞)。所以,Monte Carlo、重整化群理论等计算机模拟方法也没有考虑三维Ising模型中全局性的非平庸拓扑结构的贡献。由于这些近似方法都没有考虑非平庸拓扑结构对物理性质的贡献,它们都存在一个相同的系统误差。尽管计算精度很高,获得结果相互之间吻合得很好,但它们都不是正确的精确解。
本文重点综述在文献[23]发表后的相关研究进展。首先介绍作者建立的拓扑量子统计物理学以及其与拓扑量子场论的联系,然后介绍三维Ising模型精确解,主要是用Clifford代数和Riemann-Hilbert问题的方法证明作者提出的两个猜想。之后探究时间之本源,发现在多体相互作用体系自发产生时间。最后展望该研究方向今后的发展方向和可以研究的课题。
1 拓扑量子统计物理学
在探索三维Ising模型精确解的过程中,作者在深入理解多体相互作用体系的数学结构的基础上,提出了一系列创新的物理思想,从而创建了一种新的统计物理学──拓扑量子统计物理学。
1.1 统计物理学和量子统计物理学
经典物理学(如Newton力学)致力于研究物体之间的相互作用以及运动状态。原则上,Newton力学通过物体的运动方程可以确定性地研究其运动状态。但是,随着物体数目的增加,问题的复杂性不断增加,无法精确地求解多物体的运动方程。实际上,经典的三体问题已经是一个著名的不可精确求解的问题。当3个物体的质量(相互间的作用力)相当时,无法做微扰近似,其运动轨迹非常复杂,并敏感地依赖于初始条件,甚至可能呈现出混沌的运动状态。随着物体数目的增加,特别是在微观尺度的原子(粒子)数目是Avogadro常数量级时,问题变得异常复杂,因此急需发展出一种有效的工具,研究多粒子体系的运动状态。物质的宏观物理特性是由物质的微观结构和微观粒子间相互作用决定的。统计物理学应运而生。如何根据微观结构及微观粒子间相互作用确定物质的热力学性质是统计物理学的首要任务。统计物理学用概率统计的方法,对由性质和结构完全相同的、处于各种运动状态且各自独立的大量粒子组成系统的宏观物体的物理性质及宏观规律作出微观解释。当研究对象从少量个体变为由大量个体组成的群体时,物质的规律、性质和研究方法发生根本变化。大量粒子系统所遵循的统计规律是不能归结为力学规律的。统计物理是由微观到宏观的桥梁,它为各种材料的宏观理论提供依据,已成为气体、液体、固体和等离子体理论的基础,并广泛应用于数学、计算机、化学和生物学。
经典的统计物理学具有一些基本的假设[24~27],如遍历假设、系综。Gibbs把整个系统作为统计的个体,提出研究大量系统构成的系综在相宇中的分布,克服了气体动力学理论的困难,建立了统计物理学[24~27]。Boltzmann的基本假设是所有的微观状态等几率,属于时间系综和统计系综下的物理系统[24~27]。时间系综包含一个物理系统随时间进展的离散时间统计平均,而统计系综包含一个时间瞬间的许多系统的统计平均。在平衡态统计理论中,采用微正则系综研究能量和粒子数固定的孤立系统;采用正则系综研究可以和大热源交换能量但粒子数固定的系统;采用巨正则系综研究可以和大热源交换能量和粒子的系统。在遍历假设下,统计力学的系综是静态的,任何物理量f的系综平均是独立于时间的;对应地,它也等于f的系综平均的时间平均。原则上,时间平均和系综平均的过程是完全独立的,进行这些平均的次序是可以对调的。即,f的系综平均的时间平均等于f的时间平均的系综平均,也等于f的长时间平均(即实验值)。所以,在遍历假设下,任何物理量f的系综平均等价于一个给定系统的适当的实验测量值。系综概念的提出是建立在遍历假设基础上的。但是,仅仅在一些简单的相互作用体系严格地证明遍历假设成立,它并没有被普遍性地证明。这表明经典统计物理学的基础是不牢固的。
量子统计力学分为非平衡统计力学与平衡统计力学2大类。平衡统计力学研究平衡系统的统计规律。量子统计物理学的主要任务是从相互作用出发求出热力学函数。量子统计物理的情况比经典统计物理的情况复杂。需要引入量子力学的概念,例如波函数、概率幅、期望值等,来审视遍历假设[25]。需要用正则Hamilton重新表征量子系综,用波函数表征在系综中不同系统在某个时刻t的物理态am(t)。用概率幅表征在某个时刻测量在某个特定态下系综中找到第k系统的概率。用矩阵元素描述态密度算符,表征t时刻
1.2 拓扑量子统计物理学
如上所述,在应用量子统计物理解决三维Ising模型那样的多体相互作用体系时,出现了一系列的困难,表明在统计物理建立时提出的一些基本假设可能不再适用于这些体系。需要构建一个新的量子统计物理学,考虑到这些体系中存在的非平庸拓扑结构以及其对物理性质的贡献,定义这个新的量子统计物理学为拓扑量子统计物理学[28]。这是一个与量子力学、狭义相对论相容的统计物理学。拓扑量子统计物理学的模型有:三维Ising模型、三维Z2格点规范理论、Abelian U(1)格点规范理论、非Abelian SU(2)格点规范理论、非Abelian SU(3)格点规范理论。作者[28]证明了拓扑量子统计物理学的四个推论和一个定理,相关内容简述如下。拓扑量子统计物理学必须考虑多体相互作用体系中非平庸拓扑结构对物理性质的贡献。可以通过以下路径进行这种计算,一是在高一维空间进行规范变换来改变自旋的坐标,同时在系统的波函数(或场)上产生相因子;二是进行一个单项变换,导致带有一个单值性(monodromy)表示的平庸化映射。必须在Jordan-von Neumann-Wigner架构内构建拓扑量子统计物理学[29],利用Jordan代数进行量子算符的乘法,确保体系的可积性。拓扑量子统计物理学的有限温度下,遍历态假设被颠覆,需要进行时间平均。任何物理量f的系综平均和量子力学态平均的时间平均等于对拓扑量子统计物理体系的实验测量值,也等于物理量f的时间平均的系综平均和量子力学态平均。在拓扑量子统计物理学的模型中,在无限大温度附近产生一个拓扑相变,它经历一个时间反演对称性的对称性破缺,伴随无质量规范玻色子的产生[28]。
Klein和March[18]指出:“今后在这个领域主要的兴趣是回到张对维度D = 3的建议,建立两个猜想的精细形式,如作者指出的那样,这是文献[4]中建立的基本的统计力学的基础。”Wu等[6]指出:“(在足够高和足够低的温度)拒绝接受应用长期已知的展开到热力学极限下精确解的严格结果,这构成了对统计物理的数学基础的否定。”实际上,经典统计物理建立时就是针对动力学系统的,是有时间平均的[24~27],不过由于时间平均的复杂性,经典统计物理学就用系综平均代替了时间平均。作者认为,对于三维多体相互作用系统(包括三维Ising模型),由于三维空间与多体相互作用导致非平庸拓扑结构,在保留系综平均以及量子力学态平均的同时,必须同时进行时间平均。三维Ising模型等多体相互作用体系自发产生时间,这是对时间与空间关系的新认识,也是对统计物理学的一个贡献。作者的另外一个贡献就是发现了多体相互作用体系的拓扑相因子,这是一种新的拓扑相因子。也证明了时间平均的复杂性(不是简单地求和、求积分)。100多年前建立统计物理学时还没有量子力学的大发展,也不知道量子统计物理中三维Ising模型存在的拓扑学问题,更不清楚拓扑相因子,不可能用时间平均准确地描述动力学行为,就只能在遍历假设前提下用系综平均来描述。当然,系综平均能够成功地描述一些简单的统计物理体系,但无法准确地描述三维Ising模型这样的复杂体系。
1.3 拓扑量子场论
人们认识自然规律的途径是逐步深入的。通常经历了一个从片面到整体,从局部到全局的过程。例如,对力的认识,从万有引力、电磁力、弱力和强力,到追求4种相互作用力的统一。从对电和磁的认识,到电磁场的统一,引入场的概念。从对物质的粒子和波的属性争议,到量子力学建立波粒二象性。现代物理认为场的概念比波更基础。对于物质到底是由粒子还是由场构成的,学术界也经历了一个长期的认识过程。物理学中场论是从场的角度描述物理场和物质相互作用的物理理论。场论把某个物理量在空间一个区域内的分布称为场,包括引力场、电场、磁场、温度场、密度场等。也就是说,一个物理场可以看成在时空中某一点赋予一个(连续变化)物理量。经典场论倾向于在数学上用Lagrange量来表达,应用最小作用量原理,给出场方程和守恒定律。通常要求场论满足Lorentz协变性,以便与狭义相对论相容。量子场论是将场论与量子力学、狭义相对论相结合的物理理论,已被广泛地应用于粒子物理学和凝聚态物理学等学科中。量子场论包括量子电动力学、弱电理论、量子色动力学,分别描述电磁相互作用,电磁和弱相互作用、强相互作用。满足特定对称性的量子场论能够很好地描述除引力之外的3种相互作用。量子场论成为现代理论物理学的主流方法和工具。量子场论是高能物理和粒子物理领域的中心课题。量子场论为描述多自由度多体相互作用系统的相互作用和过程,尤其是包含粒子产生和湮灭过程,提供了有效的研究框架。弱作用和电磁相互作用实现了形式上的统一,通过Higgs机制产生质量,建立了弱电统一的量子规范理论(即Glashow-Weinberg-Salam模型)。弱电理论与量子色动力学相结合构成标准模型。
量子统计物理学与量子场论之间存在一个关键的联系[33,37,38]:实温度可以通过Wick旋转变换成虚时间。所以,(D + 1)维度的量子场论等价于D维度的量子统计物理学。根据统计物理学与量子场论的联系,作者[28]证明了拓扑量子场论的四个推论和一个定理,相关内容简述如下:拓扑量子场论必须考虑非平庸拓扑结构对物理性质的贡献,通过在高一维空间进行规范变换或者一个单项变换,同时在系统的场算符上产生拓扑相因子。注意,这里的高一维度意味着,原来的D维度的量子统计物理学变成(D + 1)维度的拓扑量子统计物理学;原来的(D + 1)维度的量子场论变成(D + 2)维的拓扑量子场论。必须在Jordan-von Neumann-Wigner架构内构建拓扑量子场论,利用Jordan代数进行场算符的乘法,确保体系的可积性。拓扑量子场论在有限温度下各态遍历假设不成立,需要进行时间平均。在拓扑量子场论中,必须用复时间(复温度)参数空间。一个函数的温度(或者虚时间)平均的实时间平均等于这个函数的实时间平均的温度(或者虚时间)平均。在拓扑量子场论的模型中,在无限大温度附近经历一个时间反演对称性的对称性破缺,产生一个拓扑相变,它对应着从虚时间(实温度)参数空间到复时间(复温度)参数空间的转变。
2 铁磁性三维Ising模型精确解
2.1 三大困难
通过对铁磁性三维Ising模型的配分函数进行分析,作者认为精确求解铁磁性三维Ising模型存在以下三大困难:非局域性、非Gauss性、非对易性[20]。
2.1.1 非局域性
通过Fermi-Γ矩阵变量,可证明在三维Ising模型中存在非局域性质的非平庸的拓扑结构。用自旋变量(σ)表达时也有拓扑效应,不过此时所有的表达式都是局域的。第3个转移矩阵 V3必须跟随前2个转移矩阵 V1和 V2中安排好的σ的顺序。按照这种顺序,一个自旋与其第三维方向上一个最紧邻自旋的相互作用,尽管是最近邻的,但它与平面中N个自旋的状态相关联。在三维Ising模型系统的确存在全局性的效应,所有的自旋都纠缠到一起。可以理解,由向上和向下自旋构成的不同的拓扑状态(例如纽结、链圈)也对三维Ising模型的配分函数、自由能以及其他物理性质有贡献。很显然,任何仅仅考虑自旋局域环境的方法,例如,普通的低温展开、普通的高温展开、Monte Carlo方法、重整化群理论,都不是精确的。
2.1.2 非Gauss性
每个Fermi-Gauss二次项对应一个旋转,它是旋转群(Lie群)的旋量表示。Lie代数的旋量表示对应于 Γ 矩阵的二次项表达式。 Γ 矩阵中高于二次项的表达式(例如ln V3)不是Lie代数的元素。所以,转移矩阵 V3中带有 Γ 矩阵高次项的e指数的元素(所谓的非线性项)不是Lie群的一个元素,从而使问题变成如何线性化高次项,使其成为可表示旋转的旋量的Lie群的一个元素。
2.1.3 非对易性
在二维可以应用Kaufman[39]的方法。因为仅仅有一个Fermi弦,所有 Γ 矩阵的乘积与转移矩阵都是可对易的,从而可以将体系投影成2个本征值分别为+1和-1的弦的子空间。对于三维Ising模型,转移矩阵 V3中有许多对j乘积因子,每个有一个内因子Wj。所以,必须同时对角化很多内因子,并且与整个 V3对易。即使每个内因子与 Γ2j 和 Γ2j + 2n - 1 ( Γ2j 和 Γ2j + 2n - 1为Pauli矩阵的直乘[4,13,20]) 2者都对易,但是2个 Γ 矩阵是反对易的,所以无法同时对角化内因子Wj, Γ2j 和 Γ2j + 2n - 1。对于一个j,用 Γ 矩阵的非线性变换,它仍与转移矩阵 V2和 V1混杂到一起。即使在转移矩阵 V3中的第j个因子对易,不同的j中的内因子Wj 与 V3中的其他因子不对易。当同时对角化不同j的所有内因子时,不同的 Γ2jΓ2j + 2n - 1在这个基下无法同时块状对角化。利用一些数学方法可重新定义2个 Γ 矩阵,成功地处理单个的j,但无法同时处理所有的j。
以上三大困难的根源是在转移矩阵中存在的内因子是非线性的,这是由于三维空间固有的非平面性和多体相互作用共同导致的长程量子纠缠所造成的。如何精确求解三维Ising模型,也就是如何解决上面的三大困难,这困扰了国际学术界近100年。为此作者提出了两个猜想,为解决这个世界难题指明了前进的方向。
2.2 两大原则
2.2.1 对称性原则
三维Ising模型的精确解必须满足系统的对称性[20]。首先,三维Ising模型的对称性要求转移矩阵 V2和 V3对精确解有相同的贡献。无论哪个晶体学方向被选择为第二或者第三维度,精确解必须保持不变。如果选择相互作用常数K'作为第二个晶体学方向,内因子(即非线性项)出现在转移矩阵 V3中。如果选择相互作用常数K"作为第二个晶体学方向,内因子将出现在转移矩阵 V2中。实际上,如果通过一个非线性变换
如果2个粒子相同(全同粒子),它们的物理量,如Hamilton量或者Lagrange量应该在交换粒子时保持不变。根据三维Ising模型的正交对称性,直角坐标系中3个轴是等价的,改变它们的顺序不改变体系的能量表达式。对称性原理广泛地应用于物理学理论的建立,如Einstein的广义相对论和Yang-Mills理论,并且被用来判断体系的产出(结果)的正确性,用对称性限制物理系统的精确解的存在形式。在三维Ising模型精确解的求解过程中,对称性原则起到一个指引作用。用最简洁的方法初步确定了精确解的表达式的基本元素,同时对证明猜想的过程也有启发性,对非线性项能量的贡献有了一个明确的限制(即无论转移矩阵中的内因子如何复杂,其贡献就是增加一个标量系数)。这再一次显示了对称性原则在解决物理学难题中不可替代的作用。
2.2.2 最大本征值原则
在热力学极限条件下,仅仅最大本征值对三维Ising模型的配分函数有决定性的贡献[20]。在求解过程还发现一个非常重要的性质——最大本征值的作用。因为配分函数正比于
用下面的例子来形象地说明最大本征值原则[20]:如果求解地球上所有山峰的高度之和,就需要在地球表面搜索所有的山峰,测量每个山峰的高度,进行求和。而如果求解地球上所有山峰的高度的m次方之和,并且m趋近于无限大,由于地球上其他山峰的高度的m次方之和都可以被忽略,所以仅仅需要测量出地球上的最高峰珠穆朗玛峰的高度即可,答案就是珠穆朗玛峰的高度的m次方。从这个例子可以看出,最大本征值原则可以极大地简化三维Ising模型精确求解的过程。实际上,在求解过程中如果不应用最大本征值原则,无法求解三维Ising模型的精确解。因为三维Ising模型的本征值有无限多个,对无限多个本征值的m次方求和,是一个不可能完成的任务。
2.3 Clifford代数方法
作者[20]发展了一个三维Ising模型的代数方法,证明了四个定理:迹不变定理、线性化定理、局域变换定理、对易性定理。这四个定理严格地证明了作者提出的两个猜想,表明在猜想基础上提出的精确解是正确的。
定理一(迹不变定理):当在三维Ising模型原始转移矩阵中的直乘增加k'项单位矩阵,三维Ising模型的配分函数改变一个因子2 k'。可以通过除法抵消这个2 k' 因子,以保持迹不变。调节单位矩阵与其他矩阵的次序可以分隔转移矩阵中不同的排的e指数因子(每排包含n个晶格点)。每排的e指数因子被单位矩阵隔离开来,以致可以将它们看成转移矩阵的分矩阵而被分别处理。定理一提供了一个方法,首先扩展三维Ising模型的维度为(3 + 1)维,然后将三维Ising模型化简,以致将Ising模型在二维流形(平面)隔离开来,成为可以精确求解的问题。与此同时,这个过程维持体系的物理性质(例如,转移矩阵的迹、配分函数、自由能和热力学性质)不变。这个方法使应用Onsager[2]和Kaufman[39]为二维Ising模型发展的一些方法成为可能。
定理二(线性化定理):可以对三维Ising模型每一排的分矩阵中的非线性项进行一个线性化过程。定理二提供了一个在二维流形(平面)处理三维Ising模型的方法。三维Ising模型全局的非线性转变成在子空间里的线性,但是仍然保持整体上的非线性特性。在整个空间无法进行的平面旋转,被分解成在一系列局部坐标(子空间)中的平面旋转。
对于一个非线性体系,不存在对应的Lie群结构,不支持一个平面内的旋转变换。而Lie群结构相关的平面旋转变换在求解二维Ising模型精确解的过程中至关重要。在证明定理一之后,获得的是一个Riemann球面。通过定理二的证明,将体系切割成许许多多的小的平面。在这些小平面内部,局部存在Lie群结构相关的旋转变换。就好像尽管地球的外表面是球面,但是在人们居住的地面可以看成是一个平地。许许多多的平面整合起来就构成了人们生活的具有弯曲表面的地球。可以想象,在一颗绕地球转动的人造卫星上,用照相机对地球表面拍照,每个照片拍到的地面区域可以看成是一个平面,将许许多多张照片组合到一起就可以构成地球的整体信息。这就是线性化定理的意义所在。
定理三(局域变换定理):可以对三维Ising模型的每一排的分转移矩阵进行一个局域变换。局域变换改变局部系统的规范,平庸化系统的非平庸拓扑结构,同时在三维Ising模型的本征矢量上产生拓扑相因子。定理三提供了一个方法,将三维Ising模型的非平庸拓扑结构平庸化,同时考虑非平庸拓扑结构对三维Ising模型的配分函数、自由能和热力学性质的贡献。三维Ising模型中产生的拓扑相因子源于复数投影Hilbert参数空间的非平庸性质,它等价于在参数空间的一个规范势,由路径的整体几何决定。
需要注意的是,线性化过程和局域变换可以被同步地或者按顺序地进行。在局域变换之后,在转移矩阵 V'中的所有因子仅仅包含 Γ 矩阵的二次项。即,具有 Γ 矩阵高次项的转移矩阵 V 被平庸化。所以,转移矩阵 V'仅仅包含Fermi-Gauss项,变成可对易矩阵。能够运用广义Yang-Baxter方程或者所谓的四面体方程对易转移矩阵 V'(U)和 V'(V)的所有因子,系统变成可积的。
定理四(对易性定理):在三维Ising模型线性化过程和局域变换过程中,算符的非对易性性质可以在Jordan-von Neumann-Wigner机制框架中应用Jordan代数处理成对易的,这可以通过对在时空中演化的三维Ising模型的t个系统进行时间平均来实现。
四个定理在引入新的一个维度方面是自洽的和互补的。在定理一、二和三中,三维Ising模型通过对原始的转移矩阵增加k'个单位矩阵的直乘以及在自旋表象中将本征矢量的维度扩展到(3 + 1)维。在定理四中,三维Ising模型通过对t个三维Ising模型的体系进行时间平均以及建立一个与Jordan-von Neumann-Wigner机制和Jordan代数相吻合的量子基被扩展到(3 + 1)维。定理四解决了在定理二和三中算符的不对易性问题并且保证了前者的正确性。至此,用四个定理严格地证明作者提出的两个猜想[20]。证明过程一直保持体系的物理性质不变(如转移矩阵的迹不变、作用量不变),将两个猜想的间隙进行了无缝连接。
总结这个工作的意义:发展了一种Clifford代数方法,证明了作者的两个猜想,从而求得了三维Ising模型的精确解,解决了这个物理学著名的百年难题。并且发展出一个新的拓扑量子统计理论。这个拓扑量子统计理论利用Jordan代数、时间平均,在(3 + 1)维度的Jordan-von Neumann-Wigner机制框架内,通过拓扑变换和规范变换来处理三维多体相互作用体系的非平庸拓扑学问题。
2.4 Riemann-Hilbert问题的方法
Riemann-Hilbert问题的方法的具体步骤如下[21,22]:通过证明三个定理来证明作者的猜想一[21]。将Clifford代数扩展为纽结/Clifford代数,其中原始的Clifford代数和它的共轭代数作为子代数,共同来描述三维Ising模型中的拓扑结构。同时,利用如下过程将三维Ising模型中纽结拓展为纽结/Clifford代数。用带有正常晶格纽结γ、2种基本纽结(圆和辫子)以及它们的交叉的纽结/Clifford代数来构建零磁场下三维铁磁性Ising模型的配分函数(见图1[21])。转移矩阵 V1和 V2贡献拓扑结构的平庸部分(圆),而转移矩阵 V3贡献体系的非平庸部分(辫子)。每一条辫子均代表平面内n个自旋之间的长程纠缠效应(转移矩阵中的非线性内因子)。对于零磁场下三维铁磁性Ising模型的配分函数的产生算符,转移矩阵 Vi (i = 1, 2, 3)可以有一个纽结γ。将纽结γ表示到Riemann面上,可以表示为:
图1
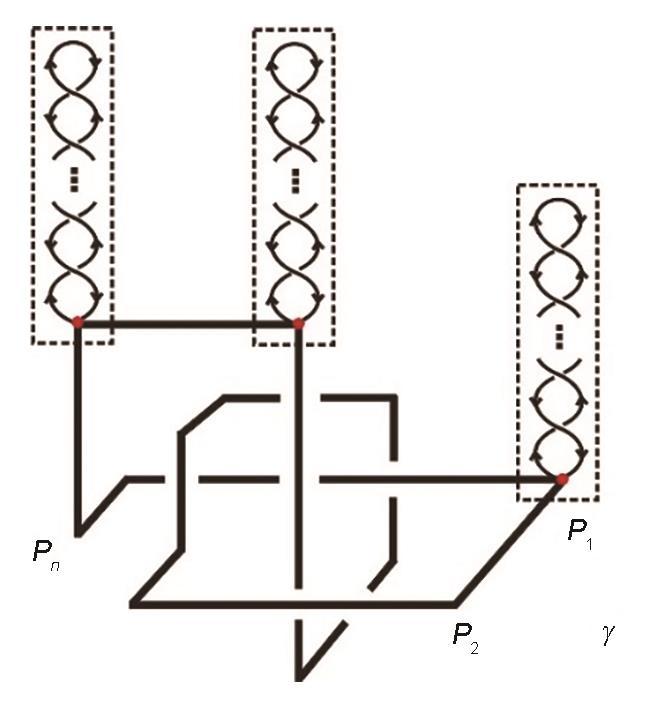
图1 与纽结γ的晶格点相连接的转移矩阵 V3 中辫子的3条举例[21]
Fig.1 Schemes illustrate three of the braids in the transfer matrix V3 connecting to the lattice points of the knot γ[21] (The circles of V1 and V2 are not shown for simplicity. Also for simplicity, the ends of the three braids are not shown to connect with the nearest neighboring lattice points along the third dimension, P1, P2, …, Pn are lattice points)
作者与Suzuki[22]通过证明另外三个定理来证明作者的猜想二。用顶角算符的乘积描述零磁场下三维铁磁性Ising模型的配分函数。用矩阵描述配分函数的磁场下三维铁磁性Ising模型的可积系统等价于平坦向量丛。用Gauu-Bonnet-Chern公式将零磁场下三维铁磁性Ising模型重整化为一个非平庸流形上的平庸模型,从而证明拓扑相因子的存在,确定了拓扑相因子。
关于Riemann-Hilbert问题的解决,再次证明作者两个猜想以及精确解的正确性。由于先后用Clifford代数方法[20]和Riemann-Hilbert问题的方法[21,22]证明了猜想,这充分表明三维Ising模型可以作为多体相互作用体系、代数、拓扑、几何等学科交叉的平台。在代数方面,应用了Clifford代数、Jordan代数、四元数代数、Lie代数、Riemann-Hilbert问题等构建数学基础;在拓扑方面,发现非平庸拓扑结构对配分函数和物理性质的贡献;在几何方面,利用单项变换去除奇异性,在三球面S3 (S代表不同维度的球面)上表示几何关系,获得几何相因子等。运用时间平均、增加单位矩阵、进行单项变换、自旋晶格与拓扑结构的映射等多种方法拓展维度。建立拓扑相因子与A-B效应、Berry相位、量子Hall效应等物理现象的联系。
2.5 铁磁性三维Ising模型精确解
式中,N为体系中自旋总数;ω'、ωx 、ωy 、ωz 为角度,数值在-π和π之间变化;
三维简单正交Ising晶格的自发磁化强度I为[4]:
式中,xi = exp(-2Ki ) (i = 1, 2, 3, 4),其中Ki = Ji / (kBT) (i =1, 2, 3) (其中Ji 为相互作用常数,kB为Boltzmann常数,T为温度,由KK* = KK' + KK" + K'K''决定简单正交Ising晶格的Curie温度[4])。对于一个简单立方Ising模型(K = K' = K''),从条件K* = 3K确定其Curie温度精确地存在于黄金点xc = exp(-2Kc) =
3 时间本源之探究
人们生来都会对大自然的奥妙产生好奇心,这种好奇心是科学研究的初心。日月星辰,春夏秋冬,动植物的生老病死,印证人们生活在一个三维空间和一维时间构成的宇宙之中。人们从哪里来?又到哪里去?是人们每个人想要知道的最基本的问题。而空间是什么?时间是什么?时空之间的关系是什么?是物理学家和哲学家感兴趣的问题。Newton提出绝对时空观,并且认为时空为背景(或者如舞台),物质以及物质间的相互作用为舞台上的演员。而Leibnitz则认为物质以及物质间的相互作用就是时空本身。如果没有了物质和物质间的相互作用,就没有了时空,根本不存在时空背景。Einstein扩展了Leibnitz的思想,提出了狭义相对论和广义相对论。狭义相对论建立了时间和空间的相对关系和质能关系。广义相对论发现了引力对时间和空间的影响。狭义相对论和广义相对论的一系列预言(如黑洞、引力波等)被实验验证,从而证明了其正确性。当然,Einstein的相对论理论并没有回答时间的本源这个问题。也就是说,时间是如何产生的仍然是一个未解之谜。这是本文试图探究的问题。
对于时间t,首先想到的是简单地对t个三维Ising模型的复制品进行加和,然后再除以t,这不改变体系的物理性质,但是也不能解决三维Ising模型问题,因为这个过程无法除去转移矩阵中的内因子,并且转移矩阵以及其中的算符仍然不对易。通过前期工作[20~22]发现,对于三维Ising模型等多体相互作用体系,可以用多种方法引入时间t,其结果是等价的。(1) 在文献[20]中定理一引入t的方法是通过在转移矩阵的直乘中引进单位矩阵并且调节其位置,保持迹不变。(2) 在(3 + 1)时空中叠放t个三维Ising模型的复制品(即t个片段),每个都具有在转移矩阵中的因子(或者算符)的位置的演化。从n个满足Jordan代数的矩阵的乘法方程很清楚地看出,在(3 + 1)时空中叠放t个三维Ising模型的复制品将导致转移矩阵(以及分转移矩阵)的Jordan代数的乘法运算成立,且互相对易[20]。(3) 构建纽结/Clifford代数,引入Riemann面从而引入时间维度,在高维度流形上求解Riemann-Hilbert问题,进行单项变换实现平庸化体系[21]。下面用图示的方法展示三维Ising模型中非平庸拓扑结构的存在、非平庸拓扑结构对热力学物理性质的贡献,并且展示时间维度是如何自发产生的[22]。这也是文献[22]中定理一的简要证明。
图2
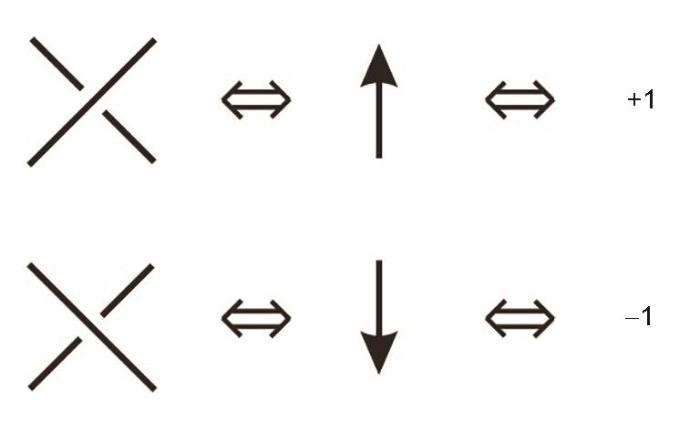
图3

图4
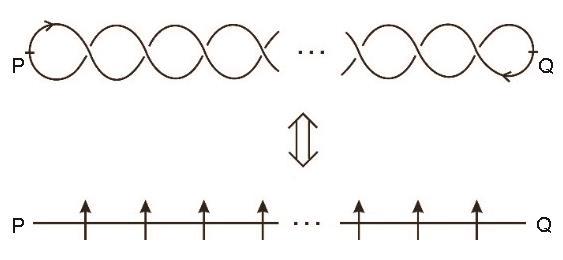
根据作者对三维Ising模型配分函数的分析,它有2种贡献,一种是自旋指向的局域贡献,一种是自旋之间长程纠缠的全局性贡献(图1[21])。可以将三维Ising模型描述成三维晶格格点上的自旋指向加上沿着第三维度方向自旋间的辫子(如图5a[22]),其中红色箭头代表局域自旋的贡献,而蓝色辫子代表非平庸的纽结结构对物理性质的贡献,属于平面内所有自旋间的长程量子纠缠。简单起见,考虑到沿着三维方向的平移对称性,在图5a[22]中仅仅给出一个晶胞。实际上,图5a[22]的表示与图1[21]的表示等价。应用图4[22]辫子与自旋链的映射关系,将图5a[22]映射为图5b[22]的结构,就可以为三维晶格格点上的自旋加上沿着第三维度方向自旋间的一条自旋链。可以看出,这一条附加的自旋链等效于在三维晶格上增加了一个新的维度,也就是说,时间维度自发产生了。
图5
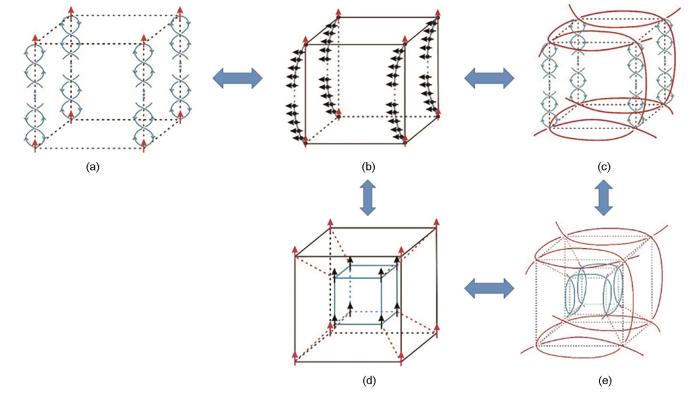
图5 三维Ising模型一个晶格单胞示意图[22]
Fig.5 Schemes illustrate a unit cell of the 3D cubic Ising lattice[22] (All the five figures can be mapped each other, in which there are two contributions to physical properties: one is local spin alignment, another is nonlocal effect of the braids)
(a) with spins (red arrows) located at every lattice site and braids (blue curves) attached to every pair of the two nearest neighboring lattice sites along the third dimension
(b) with spins (red arrows) located at every lattice site and spin chains (black arrows with blue curves) formed by the mapping from the nontrivial knots (nonlinear terms)
(c) with crossings (red curves) are mapped from spins in a unit cell of the 3D Ising lattice, and some crossings (blue curves) are attached braids from the nontrivial topological structure
(d) a unit cell of the (3 + 1)D hypercubic Ising lattice in which the spins on the original 3D Ising lattice (black lines) are represented by red arrows and the spins in the high dimensional lattice (blue lines) are represented by black arrows
(e) a example of knots with crossings located on a unit cell of the (3 + 1)D hypercubic Ising lattice.
应用图2[22]中的映射关系将图5a[22]中的局域自旋指向映射成纽结,获得图5c[22]中的拓扑结构,其中红色曲线为局域自旋指向映射的纽结结构,蓝色辫子代表自旋间长程纠缠效应。从图5b[22]可以清楚地看出,附加的自旋链等效于一个新的维度时间,可以进行一个变换,映射为如图5d[22]所示的(3 + 1)维度的时空晶格点阵,它包含局域自旋和非局域自旋链2种自旋指向的贡献。由于图5b[22]的所有晶格点(包括三维晶格点上自旋和自旋链)没有布满整个四维空间,所以图5d[22]的晶格点为(3 + 1)维度时空,并且具有一定的拓扑相因子作为从高维向三维的投影。同理,图5c[22]中的拓扑结构可以被映射为如图5e[22]所示的(3 + 1)维度的时空拓扑结构。根据拓扑学理论,在四维空间不存在非平庸的拓扑结构,所以这个映射自动将三维空间的非平庸拓扑结构平庸化。根据上述结果得出结论:由图1[21]表示的零磁场三维Ising模型的配分函数等价于由图5[22]表示的等价结构。在多体相互作用体系,由于存在自旋间的长程纠缠效应,平庸化拓扑结构的过程自发产生时间。
在统计物理中,遍历假设认为,对一个物理量在特定微观态的时间演化过程做时间平均等价于在固定时间相同的物理量对微观状态的一些统计系综的平均。接受遍历假设意味着使用统计系综是合理的,并且保证,与感兴趣的物理量的测量时间相比较,它的任意一个微观状态有效扫过系综所需要的时间足够地短。但是,如第1节所述,在三维Ising模型,在转移矩阵中存在内因子Wj 对遍历假设的合理性带来严峻的挑战。因为需要处理由那些内因子Wj 导致的非对易问题(对应于全局性效应或者非平庸的拓扑效应),不能在Ising模型的推导中忽视时间平均。作为时间平均所需要的时间必须是无限大,远长于与测量感兴趣的物理量的时间。所以,有必要对三维Ising模型的配分函数进行四重积分,去满足时间平均的要求[4]。通过这种途径,时间保留在量子统计物理的框架内,可以获得一个平衡态系统的时间平均的物理量。这个框架提供了一个构建Jordan代数的四元数序列的机会,可以应用Jordan-von Neumann-Wigner机制来处理三维Ising模型。三维Ising模型构建的四元数基是在S3球上复数四元数基[4,13]。为三维Ising模型构建的四元数基自然地表示为(3 + 1)维时空一个旋转。这个过程与一些已经非常成熟的理论紧密地联系在一起,例如:复数四元数、四元数量子力学、四元数与相对论[13]。
4 结论和展望
本文综述作者在铁磁性三维Ising模型精确解方面取得的研究进展。提出时间平均、Jordan-von Neumann-Wigner框架、拓扑结构对热力学性质的贡献等学术思想,构建了拓扑量子统计物理学。用Clifford代数方法和Riemann-Hilbert问题的方法证明作者提出的两个猜想,求出铁磁性三维Ising精确解。在此基础上,探究了时间的本源,发现三维多体相互作用体系中粒子(自旋)间相互作用自发产生时间。
由于三维Ising模型的精确解是一个学术界久攻不下的难题,这个研究方向从物理学的热点问题变成冷门。但是,蕴含在三维Ising模型的精确解中的物理本质没有随时间的改变而改变。三维Ising模型的精确解以及相关问题仍然是一个重大的物理学问题。2021年度诺贝尔奖和2022年度菲尔兹奖分别颁发给研究Ising模型的科学家[42,43],表明国际学术界对这个问题的重视。由于Ising模型是一个最基本的多体相互作用模型,获得其精确解以及求解的过程和方法必将对理解其他物理体系具有重要的指导意义。随着在求解铁磁性三维Ising模型精确解的过程中揭露出来这些体系中的共性问题,在拓扑学、代数学、几何学、凝聚态物理、统计物理、高能物理、计算机科学等领域的应用,三维Ising模型精确解的研究方向注定会从一个冷门转变成热门。建议从以下几个方面继续开展研究工作。
4.1 数学
4.2 计算机科学
在分析三维Ising模型中的拓扑学结构后,精确确定了自旋玻璃三维Ising模型的计算复杂度的下限为亚指数时间,超多项式时间[44]。这是通过物理思想解决数学和计算机领域问题的一个示范。自旋玻璃三维Ising模型可以被映射为6000多个其他的科学问题,所以这个结论可以直接推广应用,解决物理、化学、生物、数学、材料科学以及计算机领域一系列相关问题,特别是解决计算机领域的重大基础科学问题——NP (NP为非确定性多项式时间)完全问题。自旋玻璃三维Ising模型计算复杂度是6000多个NP完全问题之一。解决了一个NP完全问题就等于解决了所有的NP完全问题。最近,作者[45]将自旋玻璃三维Ising模型计算复杂度与计算机领域的Boolean可满足性(SAT)问题进行了联系。建议进行有关的研究,例如:对NP完全问题证明过程进行更严格的数学描述、在物理理论指导下对不同的计算问题进行算法优化等。另外,最近Ising计算机(或者称Ising机器)成为计算机领域的热点[46],作者在三维Ising模型精确解和计算复杂度的新突破将对这个热点问题有指导意义,并将促进不同学科的学科交叉。
4.3 理论物理、统计物理、高能物理、粒子物理
在铁磁性三维Ising模型精确解的基础上[4,20~22],作者[28]建立了拓扑量子统计物理学和拓扑量子场论的数学基础。利用Jordan代数、时间平均,在(3 + 1)维度的Jordan-von Neumann-Wigner机制框架内,通过拓扑变换和规范变换、Riemann-Hilbert问题的方法和单项变换等不同的方法来处理三维多体相互作用体系的非平庸拓扑学问题。发现了三维多体相互作用体系的拓扑相因子,发现在拓扑量子统计中遍历假设不成立,在无限大温度附近发生时间反演对称性破缺以及无质量玻色子的产生等。对理解物质之间的相互作用、拓扑学对物理性质的贡献、空间的本质、时间的自发产生等具有启发性的指导作用,并且求出三维Z2格点规范理论的精确解[47]。相关结果对理论物理、统计物理、高能物理、粒子物理等领域均有启发性指导意义。建议相关领域的研究者开展后续的理论和实验研究,特别是拓扑量子统计物理学和拓扑量子场论、无限大温度附近发生的拓扑相变以及时间反演对称性破缺和无质量玻色子的产生。
4.4 凝聚态物理
可以将获得的铁磁性三维Ising模型精确解的结果推广应用到其他物理模型体系,通过不同模型之间的映射直接应用铁磁性三维Ising模型的精确解。作者的前期工作[48]通过映射给出二维横场Ising模型的精确解,给三维经典相变和二维量子相变的研究带来新的启示。可以根据三维Ising模型、二维横场Ising模型等精确解的结果,深入研究块体磁性材料和二维磁性材料的临界温度、临界指数。通过比较三维和二维材料的临界点,获得交换作用常数以及从三维到二维的渡越。通过计算机模拟材料的临界性质(仅考虑局域贡献),与精确解(考虑了非局域的拓扑贡献)进行比较,其差值为非平庸的拓扑结构对物理性质和临界指数的贡献。或者构建考虑了非局域拓扑贡献的结构(如图5),通过计算机模拟直接计算三维Ising模型的物理性质和临界指数,并且与精确解做比较。在实验方面,系统地研究不同磁性材料的临界指数(包括比热容、自发磁化强度、低磁场下的磁化强度、磁化率、关联长度等),考虑到非平庸拓扑结构对Ising模型(以及Heisenberg模型)的临界性质的贡献,对实验结果(包括文献中的数据)进行重新分类。针对经典连续相变,还可以研究合金中的有序-无序相变、液体-液体两相共存、气-液共存、超导材料中的超导态-正常态相变、液氦中的超流-正常液体转变等。另外,通过改变磁场、电场、压力、掺杂量、有序度等物理量研究广泛存在于磁性材料、铁电材料、超导材料、金属-绝缘体转变体系、量子Hall效应体系等体系中在零温以及附近的量子相变。建议开展理论和实验研究,实验工作需要注意:保证样品质量,必须是单晶。测量温度必须精确控制,需要精确地测量相变温度以及临界磁场等物理量,特别是研究量子相变需要在极低温条件下施加外磁场、外电场、压力等,并且精确地控制和测量临界磁场、临界电场、临界压力等。







 沪公网安备31011202020290号
沪公网安备31011202020290号
