分享:Fe76Ga5Ge5B6P7Cu1 合金的非等温晶化动力学
郭璐1,2, 朱乾科 ,1,2, 陈哲1,2, 张克维
,1,2, 陈哲1,2, 张克维 ,1,2, 姜勇1,2
,1,2, 姜勇1,2
1.
2.
采用单辊旋淬法制备了Fe76Ga5Ge5B6P7Cu1带材,并研究了其晶化行为和机理。结果表明Fe76Ga5Ge5B6-P7Cu1合金的晶化过程分为2个阶段,第1个阶段为α-Fe(Ga, Ge)相的析出,第2个阶段为Fe(B, P)硬磁相的析出。在非等温加热的情况下,初始表观激活能大于晶化表观激活能。根据Johnson-Mehl-Avrami-Kolmogorov (JMAK)方程得出,对于非完全非晶结构的合金,其晶化过程为预先存在的晶核或团簇不断长大,同时伴随着新的晶核不断析出且形核率不断下降。此外,快速升温的退火工艺更适合形成均匀弥散的纳米晶组织。通过实验验证,退火时升温速率为100 K/min的合金软磁性能优于升温速率为10和50 K/min的合金,其最优起始磁导率为2.86 × 10-2 H/m,矫顽力为1.77 A/m。
关键词:
铁基非晶纳米晶软磁合金具有高磁导率、低矫顽力(Hc)、低损耗等优异的性能,可用作变压器、互感器和永磁电机等铁芯材料[1,2]。Fe73.5Si13.5Nb3B9Cu1合金(Finemet)的问世[3],使得铁基非晶纳米晶合金的研究进入高潮。但是,与硅钢相比,铁基非晶纳米晶的饱和磁感应强度(Bs)仍然较低,限制了其在电力电子行业的广泛应用。提高Bs的方法有2种:一是直接提高Fe的含量;二是添加可以提高Fe磁矩的元素(如Ga、Ge等)[4,5]。然而,这2种方法都会导致类金属元素含量的降低,从而在一定程度上降低合金的非晶形成能力,使得淬态合金为非完全非晶结构,即在非晶基体中镶嵌有细小晶粒以及团簇[6~8]。这种情况下,常规的退火工艺(慢速升温、长时间保温)会使得退火后的合金晶粒粗大且尺寸不均匀,无法获得均匀弥散的纳米晶颗粒,恶化纳米晶之间的铁磁交换耦合作用以及合金的软磁性能,如Fe85Si2B8P4Cu1 (Nanomet)合金[6]由于Fe含量高,淬态合金无法形成完全非晶结构,在退火过程中,升温速率较低(10 K/min)时析出的纳米晶尺寸较大且不均匀,矫顽力高达100 A/m,随着升温速率升高,纳米晶逐渐向细小均匀化转变,矫顽力逐渐降低,最终在升温速率为400 K/min时得到矫顽力小于10 A/m的合金;在非完全非晶结构的Fe85.5B10Si2P2C0.5合金[8]中,同样是利用极高的升温速率来获得均匀细小的纳米晶组织,该合金的矫顽力为12 A/m。由此可见,为了在提高合金Bs的同时保证较好的软磁性能,需要明确该类型合金退火过程中的晶化机制,以此为指导来调整退火工艺,这对新型材料的研发和应用具有重要的指导意义。在晶化动力学的研究过程中,Johnson-Mehl-Avrami-Kolmogorov (JMAK)方程经常被用于分析等温晶化动力学[9,10],研究[11~15]表明,如果整个形核过程发生在早期结晶过程中,那么JMAK方程也可以应用于非等温条件,因此可通过JMAK方程来分析和指导退火工艺,从而获得晶粒尺寸均匀的纳米晶结构,提高合金的软磁性能。
Zhu等[16]通过添加提高Fe磁矩的元素Ga,已经开发出Hc保持不变(0.24 A/m)、饱和磁感应强度提高11%的类Finemet合金(Fe73.5Si7.5Nb3B9Cu1Ga6)。通过进一步研究Fe77.5Si7.5Ga6B9合金发现[5],在合金晶化过程中,由于类金属Si固溶于α-Fe会导致合金在晶化体积分数较大时Bs的下降。基于此,本工作通过增加多种Fe磁矩增强元素(Ga、Ge)来提高合金的Bs,并试图通过添加不溶于α-Fe的类金属元素P,期望在保持Bs的同时提高合金的非晶形成能力和软磁性能,从而设计出Fe76Ga5Ge5B6P7Cu1合金。其中,Cu的添加可以为纳米晶的析出提供形核点、细化晶粒尺寸,起到进一步提高软磁性能的目的。本工作采用单辊旋淬法制备了Fe76Ga5Ge5B6P7Cu1带材,探讨了Fe76Ga5Ge5B6P7Cu1合金的晶化机理。为了验证计算结果,研究了升温速率对合金显微组织和软磁性能的影响。
1 实验方法
实验选用高纯(99.99%,质量分数)的Fe、Ga、Ge、B、P-Fe中间合金(P含量为25.23%,质量分数)、Cu原料,在Ar气氛围下,用真空电弧炉熔炼Fe76Ga5Ge5B6P7Cu1母合金,熔炼3次以确保成分均匀。采用单辊旋淬法制备了宽约2 mm、厚约20 μm的带材,辊轮的转速约为29.9 m/s。在N2氛围下,用NETZSCH-STA449C型差式扫描量热仪(DSC)测量了淬态合金非等温DSC曲线,加热速率β分别为5、15、25和35 K/min。在350~500℃对合金进行真空退火,升温速率分别为10、50和100 K/min,保温时间为1 min。淬态和退火后合金的结构由MiniFlex600型X射线衍射仪(XRD,CuKα 辐射源,波长0.15418 nm)检测。合金的起始磁导率(μi)和矫顽力用MATS-2010S软磁直流测量系统检测,样品尺寸为50 mm × 2 mm × 20 μm。合金退火后的显微组织用JEM 2100F透射电子显微镜(TEM)观察和分析。
2 实验结果与分析
图1a为淬态Fe76Ga5Ge5B6P7Cu1合金的XRD谱。可以看出,衍射角2θ = 45°左右处为漫散射峰,表明合金基体为非晶结构;2θ = 65°左右处为尖峰,对应于α-Fe的(200)面,表明合金已发生部分晶化。在铁基非晶态合金中当P含量增加到5%~6% (原子分数)时,容易形成表面晶化,因为晶化相晶粒的(200)面平行于带材表面,因此易于检测[17~19]。图1b为淬态Fe76Ga5Ge5B6P7Cu1合金在不同加热速率下的非等温DSC曲线。可以看出,所有的DSC曲线均有2个放热峰。第1个晶化放热峰对应一次晶化产物α-Fe软磁相从非晶基体中的析出[20,21];第2个晶化放热峰对应Fe(B, P)硬磁相从残余非晶相中的析出[21,22]。图中,Tx1和Tx2分别为2个放热峰的起始温度,Tp1和Tp2分别为峰值温度,具体数值如表1所示。可以看出,随着升温速率的升高,Tx和TP均增大,说明非晶合金的晶化表现出较明显的动力学效应,这种动力学效应表明非晶合金的晶化是一个热激活过程[15,23]。从图1b还可以看出,放热峰的形状与升温速率有关,随着升温速率的提高,放热峰的半峰宽增加,峰的不对称性加大,DSC曲线后端的圆弧拖拽现象更加明显。图1c为特征温度随lnβ的变化曲线拟合图。特征温度对加热速率的敏感性常用Lasocka经验关系式来计算[24]:
图1
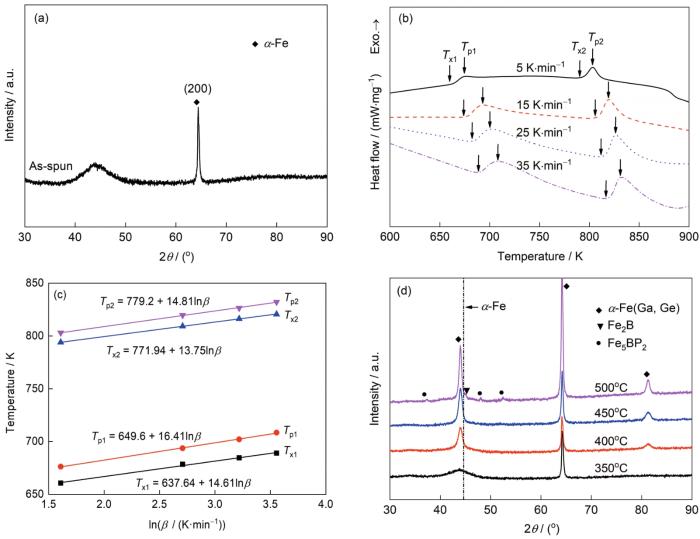
图1 淬态Fe76Ga5Ge5B6P7Cu1合金的XRD谱,在不同加热速率下的DSC曲线、特征温度(Tx1、Tp1、Tx2、Tp2)随lnβ (β为加热速率)变化的拟合曲线,以及Fe76Ga5Ge5B6P7Cu1合金不同温度退火后的XRD谱
Fig.1 XRD spectrum (a) and DSC curves (b), evolution of the characteristic crystallization temperatures (Tx1—initial exothermic temperature of the first peak, Tp1—peak temperature of the first peak, Tx2—initial exothermic temperature of the second peak, Tp2—peak temperature of the second peak) with the natural logarithm of the heating rate lnβ (β—heating rate) (c) of as-spun Fe76Ga5Ge5B6P7Cu1 ribbons, XRD spectra of Fe76Ga5Ge5B6P7Cu1 alloys annealed under different temperatures at heating rate of 100 K/min (d)
表1 淬态Fe76Ga5Ge5B6P7Cu1在不同加热速率下的特征温度 (K)
Table 1
| β / (K·min-1) | Tx1 | Tp1 | Tx2 | Tp2 |
|---|---|---|---|---|
| 5 | 660.65 | 676.23 | 793.98 | 803.09 |
| 15 | 678.44 | 693.66 | 809.30 | 819.64 |
| 25 | 684.49 | 702.11 | 816.33 | 826.43 |
| 35 | 689.04 | 708.41 | 820.63 | 832.22 |
式中,〈T〉为特征温度(Tx1、Tp1、Tx2、Tp2),β为加热速率,A和B为系数。B是衡量特征温度对加热速率敏感性的系数,因为B为拟合曲线的斜率,B值越大,代表特征温度对加热速率的改变越敏感,B值越小,特征温度对加热速率的敏感性越差。从图1c可以看出Tp1对加热速率的敏感性最大。
为了进一步证明DSC曲线所对应的2个放热峰的析出相,图1d所示为在350~500℃升温速率为100 K/min的Fe76Ga5Ge5B6P7Cu1合金XRD谱。在400℃时,合金已经开始晶化,纯α-Fe在XRD谱中第一个衍射峰的位置为2θ = 44.673°,图1d中α-Fe第1个衍射峰的角度均向左偏移。根据Bragg方程:
式中,d为晶面间距,θ为掠射角,N为反射级数,λ为X射线波长。
为了分析Fe76Ga5Ge5B6P7Cu1非晶合金的晶化行为和热稳定性,通过Kissinger方程[25]和Ozawa方程[26]计算了初始表观激活能(Ex)和晶化表观激活能(Ea),公式如下:
式中,E为表观激活能(Ex、Ea),R为气体常数(R = 8.314 J/(K·mol)),C为常数。以Kissinger方程为例,1 / T (T为温度)为X轴,ln(β / T2)为Y轴,将表1中不同升温速率对应的特征温度(如Tx1)代入可得到4个点,对这4个点进行线性拟合,根据斜率即可求出表观激活能(如第1个峰的初始表观激活能(Ex1)为(245.86 ± 3.9) kJ/mol),依此方法,根据Tp1、Tx2、Tp2分别对应求出第1个峰的晶化表观激活能(Ea1)为(230.62 ± 0.83) kJ/mol,第2个峰的初始表观激活能(Ex2)为(379.84 ± 2.77) kJ/mol,第2个峰的晶化表观激活能(Ea2)为(360.58 ± 3.384) kJ/mol。通过Ozawa方程计算得出,Ex1为(244.45 ± 14.7) kJ/mol,Ea1为(230.24 ± 6.45) kJ/mol,Ex2为(373.96 ± 21.68) kJ/mol,Ea2为(355.80 ± 26.68) kJ/mol。从图2可以看出,数据点几乎都在拟合的直线上,说明利用Kissinger方程和Ozawa方法计算Fe76Ga5Ge5B6P7Cu1非晶薄带的激活能是合理的。表观激活能代表原子间的相互作用,激活能越大,原子间的相互作用越强,即结晶过程中需要克服的能垒越高,说明热稳定性越高[15]。可以看出,利用上述2种方法计算的表观激活能均为Ex1 > Ea1,表明生成α-Fe(Ga, Ge)形核所需的能垒大于长大所需的能垒。这可能是由于Fe76Ga5Ge5B6P7Cu1中有Ga和Ge,由于Ga和Ge为大尺寸原子,形核过程中原子扩散受阻,导致形核过程需要克服更高的能垒。当Ga和Ge通过扩散与Fe形核后,在残余非晶相内留下较大的原子间隙,为后续原子的扩散提供通道,导致晶粒长大过程中的扩散阻力小于形核过程,宏观表现为长大激活能小于形核激活能。另外,Ea2 > Ea1,表明析出Fe(B, P)硬磁相所需克服的能垒大于生成α-Fe(Ga, Ge)所需克服的能垒。这可能是由于已经析出的α-Fe(Ga, Ge)相阻碍了原子的扩散,导致Fe(B, P)相的析出更加困难。
图2
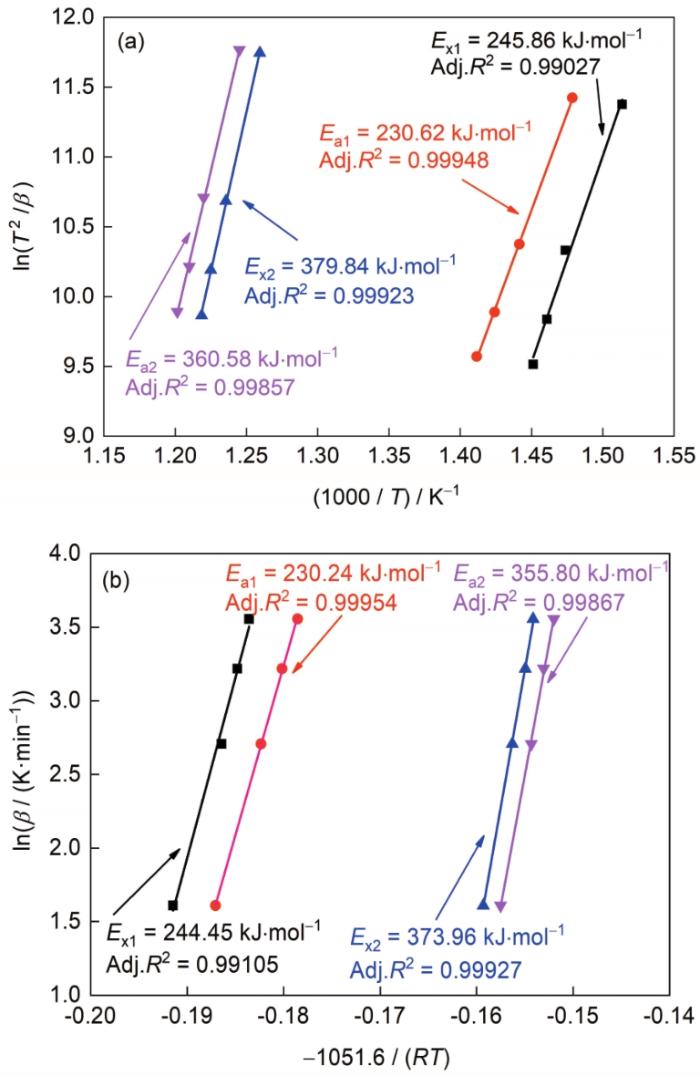
图2 淬态Fe76Ga5Ge5B6P7Cu1合金采用Kissinger和Ozawa方程的拟合图
Fig.2 Fitting plots by Kissinger (a) and Ozawa (b) equations in as-spun Fe76Ga5Ge5B6P7Cu1 ribbons (Ex1—initial activation energy of the first peak, Ea1—apparent activation energy of the first peak, Ex2—initial activation energy of the second peak, Ea2—apparent activation energy of the second peak; T—temperature, R—gas constant, Adj.R2—goodness of fit)
图3为在不同加热速率下DSC曲线中每个峰的晶化体积分数(α)随温度的变化图。α可以用以下公式来计算[27]:
图3
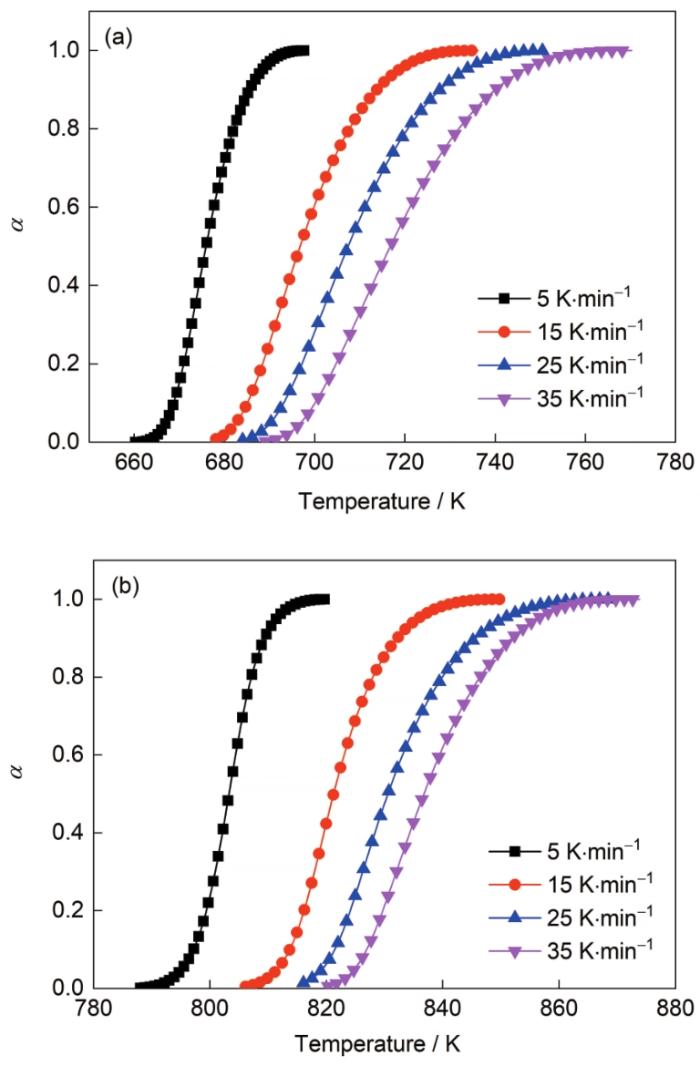
图3 在不同的加热速率下第1个峰和第2个峰晶化体积分数(α)随温度的变化
Fig.3 Evolutions of crystallization fraction (α) with temperature for the first peak (a) and the second peak (b) at different heating rates
式中,A(T)为温度为T时DSC曲线上放热峰的面积,A∞ 为整个放热峰的面积。从图3可以看出,在所有的加热速率下,随着温度的升高,晶化体积分数曲线均呈S型分布,表明Fe76Ga5Ge5B6P7Cu1合金的晶化过程可以分为3个阶段:第1阶段:α = 0,晶化反应还未进行,0 < α < 0.1,形核占主导地位,晶化转换很小;第2阶段:0.1≤ α ≤ 0.9,随着晶化体积的不断增加,体积自由能下降,晶态和非晶态之间的界面增加,使得界面自由能增加;第3阶段:0.9 < α < 1,晶态和非晶态之间的界面能减小,晶化逐渐停止,α = 1,晶化反应已经停止[12,14]。
晶化过程中局域的Avrami指数(n)常用来分析晶化机理。非晶等温晶化的JMAK方程[28]如下所示:
图4为Avrami指数随晶化体积分数的变化图。可以看出,第1个峰和第2个峰n值分布均在0~2.5之间(α逼近0和1的情况不考虑)。晶化过程中的形核和长大行为可以进一步用以下公式[14,29]来表示:
图4
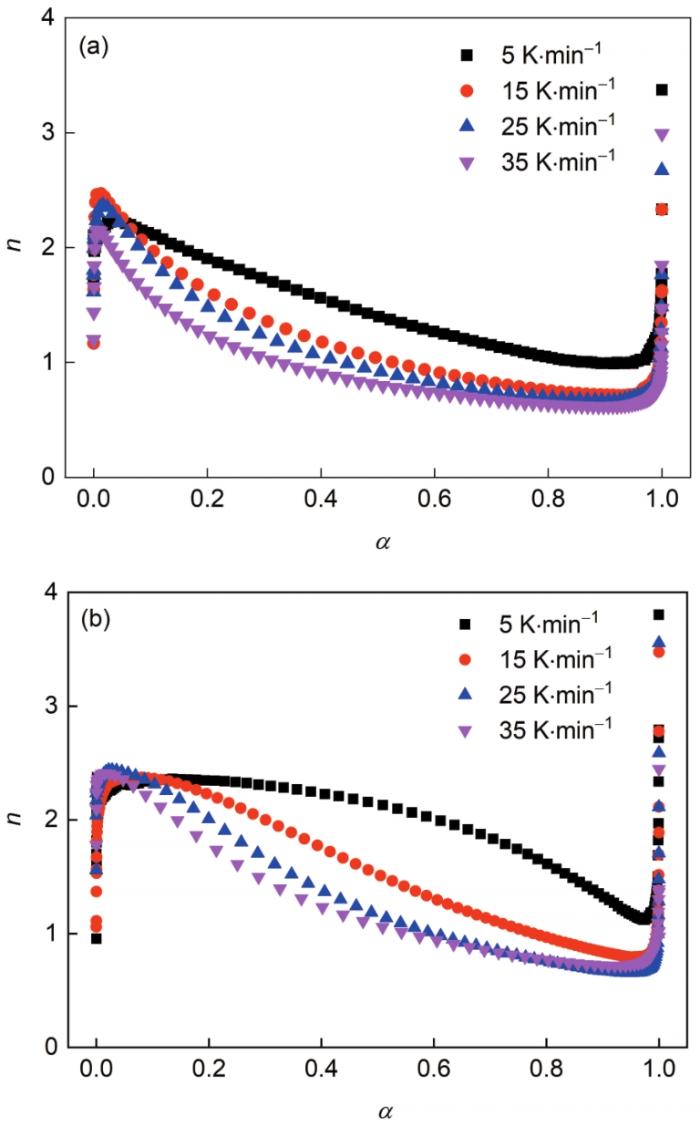
图4 第1个峰和第2个峰的Avrami指数(n)随α的变化
Fig.4 Evolutions of the Avrami exponent (n) as a function of α during crystallization for the first peak (a) and the second peak (b)
式中,a是与形核有关的参数,a = 0代表形核率为0,0 < a < 1代表形核率下降,a = 1代表形核率不变,a > 1代表形核率增加;b是与生长维度有关的参数,b可以取值1、2、3;p是与生长方式有关的参数,p = 0.5代表扩散型生长,p = 1代表界面型生长。已有研究[15,30]表明铁基非晶合金是通过扩散生长的,因此p = 0.5。总之,当1.5 < n < 2.5,代表合金在形核的同时在已有晶核的位置开始生长,且形核率下降。当n ≤ 1.5,形核率为0,晶体呈扩散型生长。
表2所示为DSC曲线中第1个峰的机理表征参数。当β = 5 K/min,0 ≤ α ≤ 0.4时,0 < a < 1,表明晶化初期,在形核的同时预先存在的晶核也在长大,且形核率不断下降;0.4 < α ≤ 1时, a = 0,表明合金已经不再形核。当β = 15和25 K/min,0 ≤ α ≤ 0.2时,0 < a < 1,形核率减小;0.2 < α ≤ 1时,a = 0,形核率为0。当β = 35 K/min,0 ≤ α ≤ 0.1时,0 < a < 1,形核率减小;0.1 < α ≤ 1时,a = 0,形核率为0。由此可见,升温速率较低时,形核过程跨越范围较大,而预先存在的晶核率先长大,这将导致合金中析出的纳米晶颗粒尺寸差别较大;当升温速率较高时,合金的形核过程集中在晶化体积分数较低时,随着晶化体积分数的增加,新形成的晶核和预先存在的晶核同时长大,最终形成尺寸均匀的纳米晶组织。因此对于非完全非晶结构的合金,较快的升温速率更利于形成均匀的纳米晶组织。
表2 第1个峰晶化机理的表征参数
Table 2
| β / (K·min-1) | α | n | a | b | p |
|---|---|---|---|---|---|
| 5 | 0 ≤ α ≤ 0.4 | 1.5 < n < 2.5 | 0 < a < 1 | 3 | 0.5 |
| 0.4 < α ≤ 1 | n ≤ 1.5 | a = 0 | 3 | 0.5 | |
| 15, 25 | 0 ≤ α ≤ 0.2 | 1.5 < n < 2.5 | 0 < a < 1 | 3 | 0.5 |
| 0.2 < α ≤ 1 | n ≤ 1.5 | a = 0 | 3 | 0.5 | |
| 35 | 0 ≤ α ≤ 0.1 | 1.5 < n < 2.5 | 0 < a < 1 | 3 | 0.5 |
| 0.1 < α ≤ 1 | n ≤ 1.5 | a = 0 | 3 | 0.5 |
表3所示为DSC曲线中第2个峰的机理表征参数。当β = 5 K/min,0 ≤ α ≤ 0.8时,形核率下降;0.8 < α ≤ 1时,形核率为0。当β = 15 K/min,0 ≤ α ≤ 0.5时,形核率减小;0.5 < α ≤ 1时,形核率为0;当β = 25和35 K/min,0 ≤ α ≤ 0.3时,形核率减小;0.3 < α ≤ 1时,形核率为0。可见升温速率较低时,第2个峰的形核过程跨度更大,这种持续性的边形核边长大的状态会导致晶粒尺寸不均匀,当升温速率升高时,形核过程跨度较小,晶化过程表现为先形核,然后预先存在的晶核和新形成的晶核同时长大,进一步说明对于非完全非晶合金,快速升温更有利于集中形核,晶核同时长大。
表3 第2个峰晶化机理的表征参数
Table 3
| β / (K·min-1) | α | n | a | b | p |
|---|---|---|---|---|---|
| 5 | 0 ≤ α ≤ 0.8 | 1.5 < n < 2.5 | 0 < a < 1 | 3 | 0.5 |
| 0.8 < α ≤ 1 | n ≤ 1.5 | a = 0 | 3 | 0.5 | |
| 15 | 0 ≤ α ≤ 0.5 | 1.5 < n < 2.5 | 0 < a < 1 | 3 | 0.5 |
| 0.5 < α ≤ 1 | n ≤ 1.5 | a = 0 | 3 | 0.5 | |
| 25, 35 | 0 ≤ α ≤ 0.3 | 1.5 < n < 2.5 | 0 < a < 1 | 3 | 0.5 |
| 0.3 < α ≤ 1 | n ≤ 1.5 | a = 0 | 3 | 0.5 |
μi和Hc是组织结构敏感参数,它们的大小取决于晶粒尺寸(D)及其分布情况,当晶粒尺寸小于铁磁耦合交换作用长度(Lex)时,晶粒均匀弥散分布,有利于提高纳米晶相间的磁交换耦合作用,进而改善合金的综合软磁性能[31]。图5显示不同升温速率和退火温度下μi和Hc的变化。可以看出,随着退火温度的增加,μi均呈先增加后降低的趋势,Hc均呈先下降后升高的趋势,这是因为随着退火温度的升高,合金中的应力得到释放,且逐渐析出纳米晶,由于Hc ∝ D6,μi ∝ D-6 [31],当晶粒尺寸较小时,合金的软磁性能最佳。退火温度继续升高,纳米晶的晶粒尺寸逐渐增大,因此μi减小,Hc增大。当升温速率为10 K/min时,μi较低,Hc较高,这是由于升温速率较低,预先存在的晶核在升温过程中先长大,与新形成的晶核长大不同步,导致晶粒尺寸不均匀,如图6a所示。根据图6a插图中的选区电子衍射(SAED)花样可知,合金以10 K/min的升温速率在400℃退火后的析出相为α-Fe,但由于升温速率较低,析出相结构出现了多个晶粒融合的现象,导致晶粒尺寸差更大,经Gauss拟合发现晶粒尺寸范围跨度大,恶化了纳米晶之间的磁交换耦合作用,使得软磁性能较差。当升温速率为100 K/min时,μi较大,Hc较小,在425℃时,软磁性能最优,μi为2.86 × 10-2 H/m、Hc为1.77 A/m,如图5所示。这是因为当升温速率较高时,合金在短时间内集中形核,新形成的晶核和预先存在的晶核同时长大,最终形成尺寸均匀的纳米晶组织,如图6b所示,经Gauss拟合,合金的晶粒尺寸集中在7~9 nm,细小均匀的纳米晶之间较强的磁交换耦合作用极大地改善了合金的软磁性能。这同时也验证了前面非等温晶化动力学的分析,即对于非完全非晶结构的合金,退火时升温速率越快,晶粒尺寸越均匀,软磁性能越好。
图5
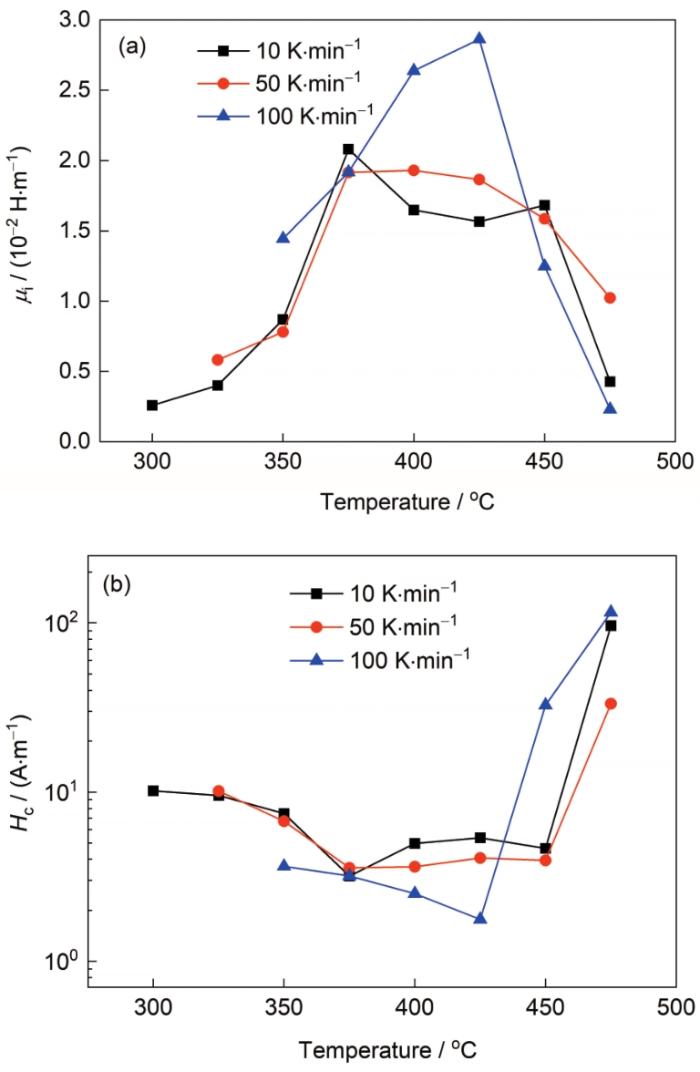
图5 不同升温速率下起始磁导率(μi)和矫顽力(Hc)随退火温度的变化
Fig.5 Initial permeability (μi) (a) and coercivity (Hc) (b) versus annealing temperature at different heating rates
图6
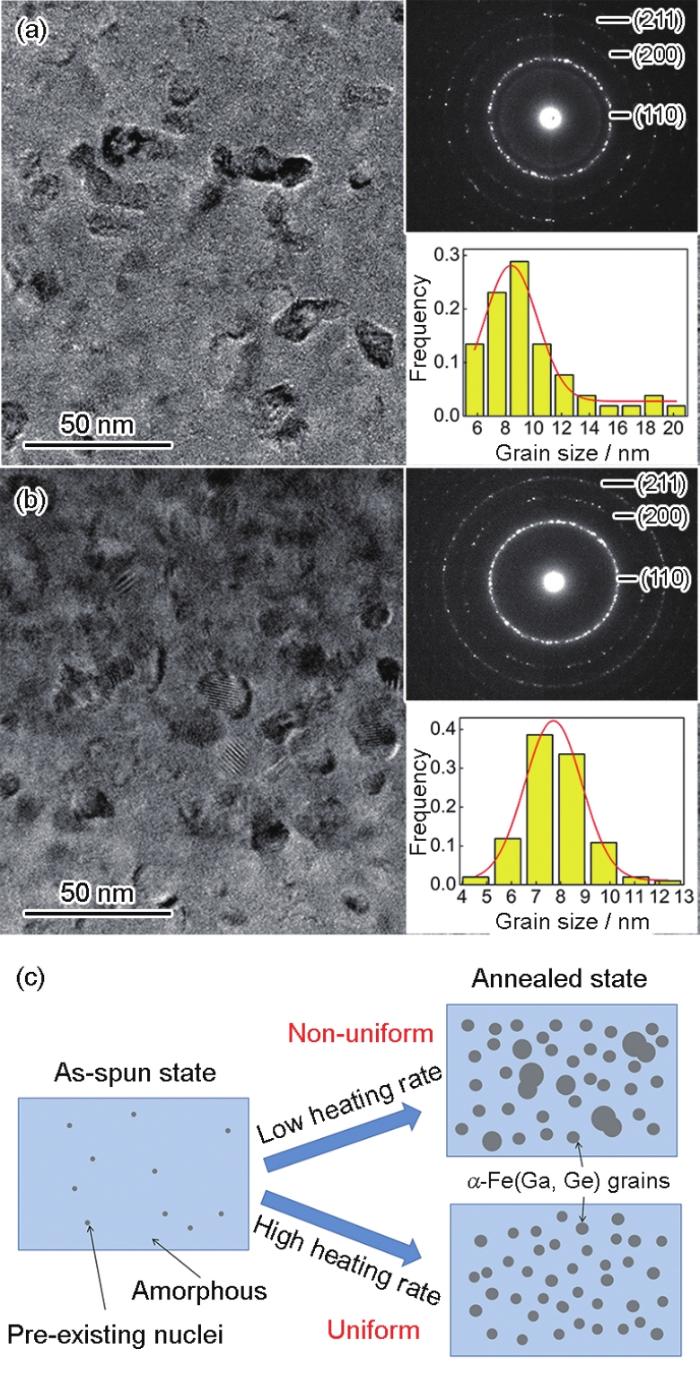
图6 升温速率10 K/min、退火温度400℃和升温速率100 K/min、退火温度425℃时Fe76Ga5Ge5B6P7Cu1合金退火后的TEM像、SAED花样和晶粒尺寸分布及晶化示意图
Fig.6 TEM images, SAED patterns, and grain size distributions of Fe76Ga5Ge5B6P7Cu1 ribbons annealed at 400oC with heating rate of 10 K/min (a) and 425oC with heating rate of 100 K/min (b), and schematic of the crystallization of Fe76Ga5Ge5B6P7Cu1 alloys (c)
基于以上分析,图6c给出了Fe76Ga5Ge5B6P7Cu1合金的晶化示意图。由于淬态合金中存在晶核或者团簇,当退火过程中升温速率较低时,合金的形核过程跨度较长,导致预先存在的晶核先长大,而新形成的晶核随后长大,这种长大不同步的现象,使得析出的纳米晶尺寸不均匀,并出现多个晶粒融合的现象,进一步增加晶粒尺寸。当升温速率较高时,合金在短时间内形核,且预先存在的晶核和新形成的晶核同时长大,形成致密均匀的纳米晶组织,提高了合金的软磁性能。可见,使用JMAK方程来分析合金的非等温晶化动力学并以此来指导合金的退火工艺是可行的。
3 结论
(1) Fe76Ga5Ge5B6P7Cu1合金非等温DSC曲线有2个放热峰,第1个峰的析出相为α-Fe(Ga, Ge),第2个峰的析出相为Fe2B和Fe5BP2。
(2) 初始表观激活能大于晶化表观激活能,这是由大尺寸原子Ga和Ge在形核和长大过程中的扩散规律导致的。
(3) 对于非完全非晶结构的合金,快速升温的退火工艺更容易得到均匀弥散的纳米晶组织,升温速率为100 K/min时,合金的μi为2.86 × 10-2 H/m,Hc为1.77 A/m。
来源-金属学报





 沪公网安备31011202020290号
沪公网安备31011202020290号
