分享:GH4169合金拘束相关的疲劳裂纹萌生寿命
1.
2.
3.
以GH4169镍基高温合金为研究对象,基于低周疲劳率相关的晶体塑性本构,引入累积能量耗散和累积塑性滑移2种疲劳指示因子作为疲劳裂纹萌生判据,对不同微缺口深度和长度下的疲劳裂纹萌生寿命进行研究。并基于统一拘束参数Ap,进一步考察拘束与疲劳裂纹萌生寿命的关联。结果表明:2种疲劳指示因子均可较好地预测疲劳裂纹萌生寿命。随着微缺口深度的增加,疲劳裂纹萌生寿命逐渐减少;随着微缺口长度的增加,疲劳裂纹萌生寿命逐渐增加。在不同的微缺口深度和长度下,疲劳裂纹萌生寿命均与
关键词:
在疲劳损伤行为方面,尚德广等[7,8]对GH4169合金在多轴载荷下的力学响应和疲劳损伤进行了研究,指出疲劳寿命和循环硬化或软化特性不仅取决于加载路径,还取决于加载顺序和加载参数。Sun等[9,10]提出了基于临界平面法的多轴疲劳损伤参数用于计算恒定高温下的纯疲劳损伤,并将循环稳定时最大等效应力的一半当量为蠕变应力,以评估多轴蠕变疲劳损伤。Prasad等[11]研究表明,加载波形对GH4169疲劳载荷下的损伤程度和滞后回线形态有显著影响,且在较低应变速率下GH4169合金存在应变时效现象。在疲劳寿命方面,Walz和Riesch-Oppermann[12]基于断裂力学理论和一阶可靠性分析方法,建立了考虑涡轮盘质量和寿命的随机模型。Wei和Yang[13]针对GH4169材料,发展了基于疲劳损伤参数的寿命预测模型,可以预测不同应变幅下的低周疲劳寿命,预测结果在± 2倍误差带范围内。Ayyappan等[14]给出了剩余寿命预测流程,并通过± 3σ (σ代表标准差)应力-应变曲线的统计分析得到了涡轮盘的概率剩余寿命。
然而,上述工作主要在宏观尺度下展开。随着研究的深入,人们发现仅凭宏观尺度下的研究还不足以完全理解疲劳行为,微观尺度下疲劳行为的研究工作相继出现。在实验方面,Krupp[15]研究表明第二相粒子的弹性模量和硬化模量与基体存在较大差异,在γ
无论在宏观尺度或微观尺度下,拘束均是影响材料疲劳行为的重要因素。拘束可以看作结构对裂尖区材料塑性变形的阻碍,与三轴应力状态密切相关。影响拘束的因素包括裂纹尺寸、试样或结构几何、材料性能失配等方面。通常将裂纹尺寸和试样或结构几何所引起的拘束效应称为几何拘束,将材料性能失配所引起的拘束效应称为材料拘束。拘束的变化会引起疲劳裂纹扩展行为的改变。在现有标准中,疲劳裂纹扩展速率往往采用标准试样在实验室测得,但是在相同应力水平下,工程结构实际工况与实验室条件往往并不一致,与此同时,不同拘束试样和结构的裂纹扩展速率也会存在差别。一些学者观察到高拘束会降低疲劳裂纹扩展速率[28~30],也有学者观察到了相反的现象[31]。一些学者发现拘束效应对Paris区和近门槛值区的疲劳裂纹扩展速率都有影响[29,32],也有研究[30]表明拘束效应的影响只存在于近门槛值区。Yang等[33]在最近研究中表明拘束对疲劳裂纹扩展速率的影响与加载方式有关。当用较快的疲劳裂纹扩展速率评定具有较慢疲劳裂纹扩展速率结构的完整性时会产生过于保守的评定结果,从而导致不必要的维修或报废,产生较大的经济损失;反之,当用其评定具有更快疲劳裂纹扩展速率结构的完整性时,可能得到非保守的结果,从而产生危险。
为了准确理解材料的疲劳行为,需要在研究中兼顾疲劳与拘束效应,但目前尚缺乏有关拘束效应对GH4169合金疲劳裂纹萌生寿命的影响研究。鉴于此,本工作基于晶体塑性有限元法,分别选用累积塑性滑移和累积能量耗散2种疲劳指示因子作为疲劳裂纹萌生判据,对不同微缺口深度和长度下(即不同拘束下)的GH4169合金疲劳裂纹萌生寿命进行研究。并基于统一拘束参数Ap,进一步探究疲劳裂纹萌生中的拘束效应,以建立拘束与疲劳裂纹萌生寿命的关联。
1 晶体塑性理论
式中, Fe为晶格畸变和刚性转动所产生的变形梯度,表征弹性部分; Fp为晶体沿着滑移方向的均匀剪切所产生的变形梯度,表征塑性部分。
对于由剪切产生的塑性变形,塑性速率梯度 Lp可以表示为与塑性滑移率
式中,
在经典唯象本构模型中,通常使用临界剪切应力
其中,剪切应力与当前应力状态相关[35]:
式中,S为第二类Piola-Kirchhoff应力。
在第α个滑移系中,
式中,
式中,q为潜硬化系数,通常取1~1.4,本工作中q取1[36];参数h0、
本模型通过引入背应力参量
式中,C代表直接硬化模量,D代表动态回复模量。
晶体塑性理论框架通过用户材料自定义子程序UMAT嵌入ABAQUS软件中,实现对材料疲劳行为的描述。此外,为了表征材料的损伤程度,并确定疲劳裂纹萌生寿命,引入2种疲劳指示因子——累积能量耗散W、累积塑性滑移P,作为微观疲劳裂纹萌生判据[37]。
W可通过
P可通过 Lp定义[37]:
W和P均与循环周次呈线性关系[37],根据测定的临界累积能量耗散Wcrit、临界累积塑性滑移Pcrit和单周循环能量耗散Wcyc、单周循环塑性滑移Pcyc,通过
2 方案设计和有限元建模
2.1 材料
2.2 代表体积单元建立
图1

图1 GH4169镍基高温合金的代表体积单元(RVE)
Fig.1 A representative volume element (RVE) of GH4169 nickel base superalloy
2.3 方案设计
图2
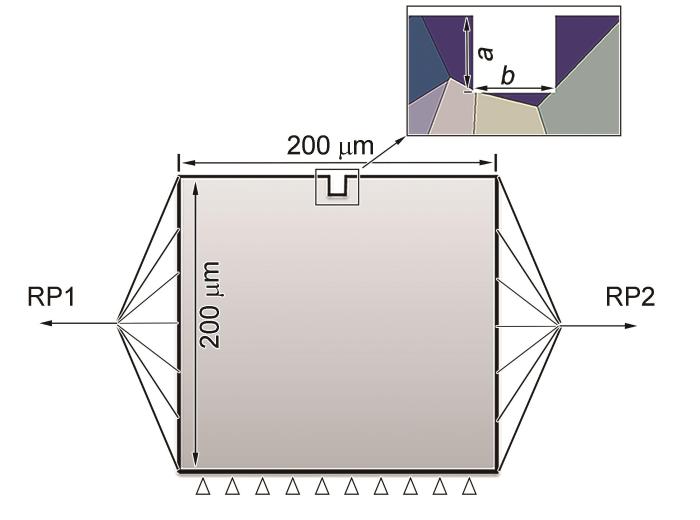
图2 模型加载与尺寸示意图
Fig.2 Schematic of model loading and geometry (a—micro-notch depth, b—micro-notch length, RP—reference point)
2.4 有限元建模
在RVE建立的基础上,通过Python语言读取其拓扑信息,并在ABAQUS软件中生成基于二维平面应变的多晶模型。分别读取每个晶粒的取向,随材料参数一起赋给每个晶粒。在模型左右两侧建立参考点,如图2所示,参考点分别与左右两边进行耦合,通过在参考点处施加位移载荷的方式控制加载,加载波形为三角波。为了消除刚体位移的影响,对底边沿y方向的位移进行约束,且允许其在x方向上自由移动。模型网格采用四节点平面应变单元(CPE4),为了避免网格尺寸对计算结果产生影响,分别对模型划分不同尺寸(2、1和0.5 μm)的网格进行网格无关性验证,如图3所示。由图可见,当网格尺寸降到1 μm时,计算结果不再随网格尺寸的变化而发生改变,故本工作所用的网格尺寸为1 μm。
图3
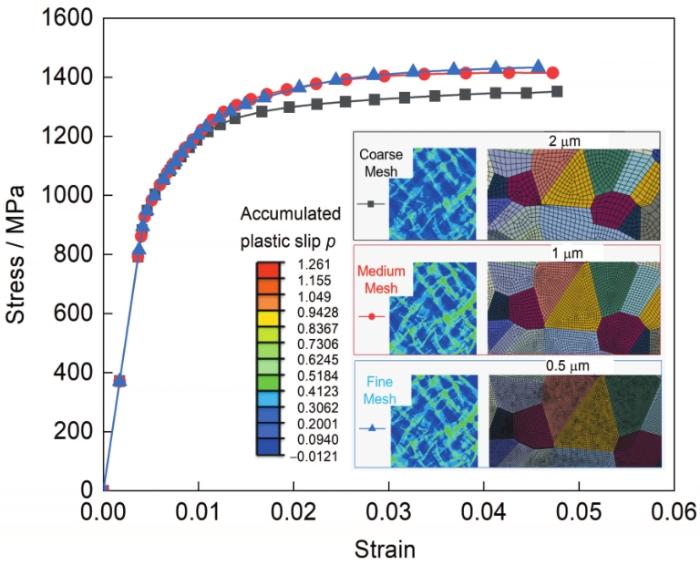
图3 基于3种不同网格尺寸所得到的应力-应变曲线和塑性滑移云图
Fig.3 Stress-strain curves and plastic slips based on three different mesh sizes
3 拘束对疲劳裂纹萌生的影响
3.1 不同微缺口深度
3.1.1 累积能量耗散
应变幅
图4

图4 应变幅为0.6%时不同微缺口深度模型在循环10 cyc后的累积能量耗散
Fig.4 Accumulated energy dissipation illustrations of models with different micro-notch depths when the strain amplitude
(a) a = 15 μm (b) a = 45 μm
(c) a = 75 μm (d) a = 105 μm
在3种应变幅(
图5
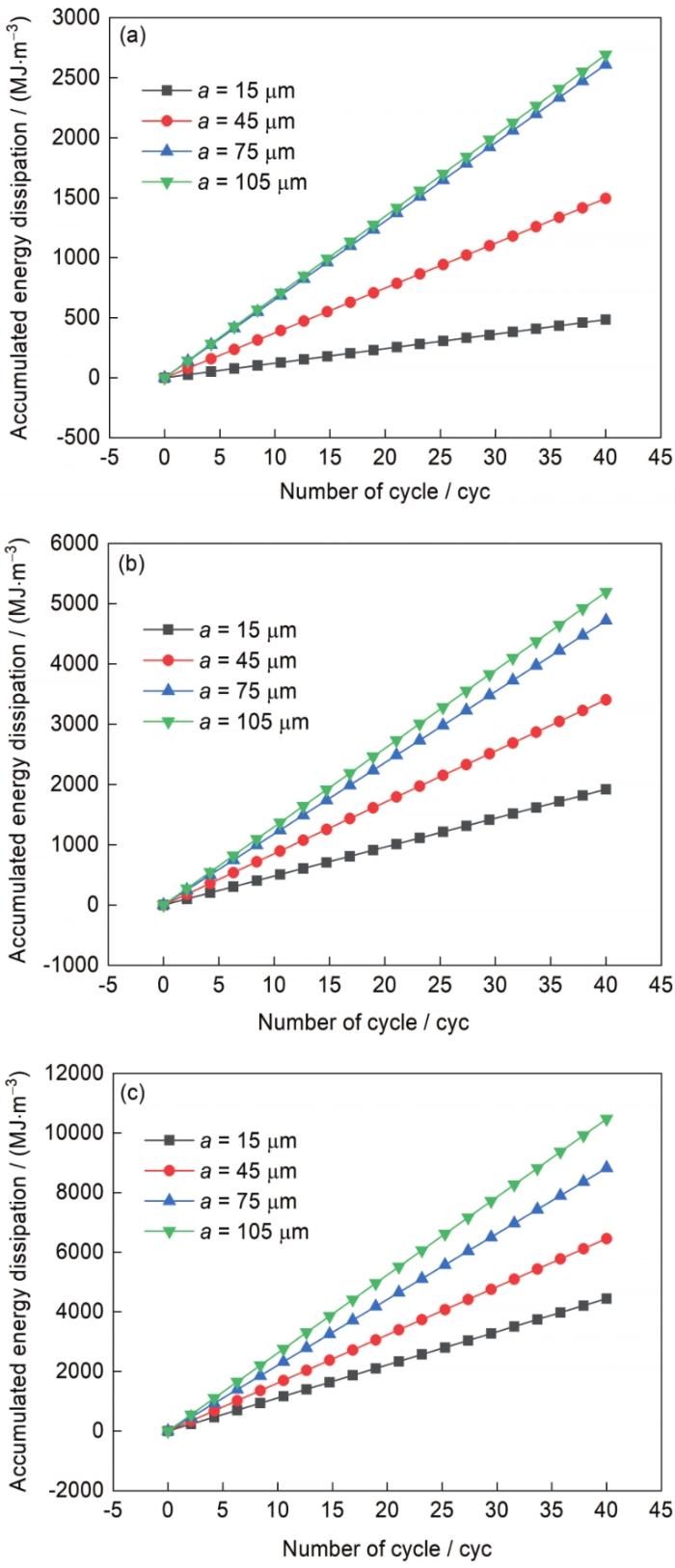
图5 累积能量耗散与循环周次间的关系
Fig.5 Relationships between accumulated energy dissipation and cycle number
(a)
以上结果可以从滞后回线的变化中得到很好的解释。选取微缺口左下角点,对其在应变幅0.6%、不同微缺口深度、循环第10 cyc时的滞后回线进行考察,如图6所示。由图可见,随着微缺口深度的增加,滞后回线的应力变化范围逐渐增大、应变变化范围基本一致,这与微缺口尺寸变化方向和加载方向有关。此时微缺口变化方向与加载方向垂直,随着微缺口深度增加,微缺口应变基本保持不变,但应力随拘束的增加越来越大。
图6
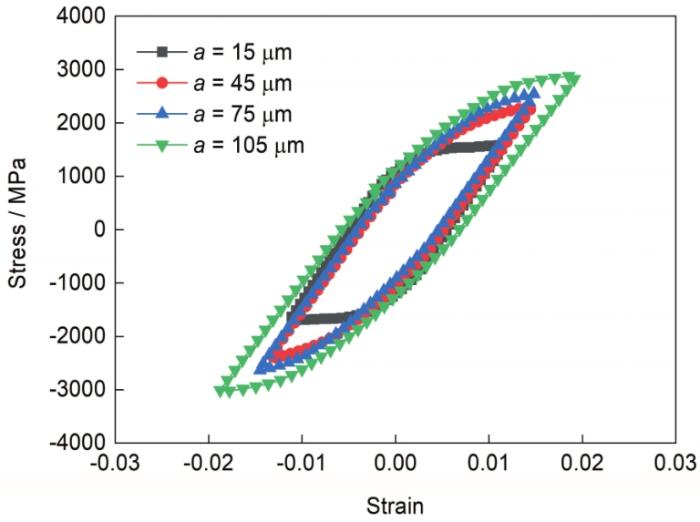
图6 应变幅为0.6%时微缺口左下角点在循环第10 cyc时的滞后回线
Fig.6 Hysteresis loops of the point at the lower left corner of the micro-notch at
3.1.2 累积塑性滑移
应变幅为0.6%时,4个微缺口深度模型在循环10 cyc后的累积塑性滑移如图7所示。由图可见,与累积能量耗散规律一致,在相同的循环周次下,随着微缺口深度的不断增加,累积塑性滑移不断增加。
图7
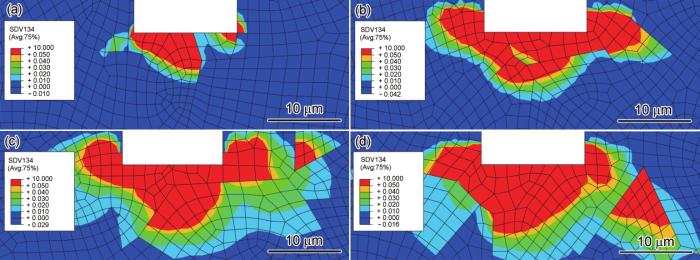
图7 应变幅为0.6%时不同微缺口深度模型在循环10 cyc后的累积塑性滑移
Fig.7 Accumulated plastic slip illustrations of models with different micro-notch depths when
(a) a = 15 μm (b) a = 45 μm (c) a = 75 μm (d) a = 105 μm
不同应变幅下,不同微缺口深度模型累积塑性滑移与循环周次间的关系如图8所示。由图可见,与累积能量耗散一致,累积塑性滑移与循环周次也呈线性关系,塑性滑移的累积速率也是恒定的。且随着微缺口深度的增加,塑性滑移的累积速率逐渐加快。与能量耗散相比,塑性滑移累积速率随着拘束的增加而趋于稳定的趋势不明显。应变幅的增加会显著提高累积塑性滑移和塑性滑移累积速率(以a = 105 μm微缺口深度为例,在循环40 cyc后,应变幅为0.6%时,累积塑性滑移为2.48,塑性滑移累积速率为0.062 cyc-1;应变幅为0.8%时,累积塑性滑移为4.67,塑性滑移累积速率为0.12 cyc-1;应变幅为1.0%时,累积塑性滑移为8.27,塑性滑移累积速率为0.21 cyc-1)。
图8
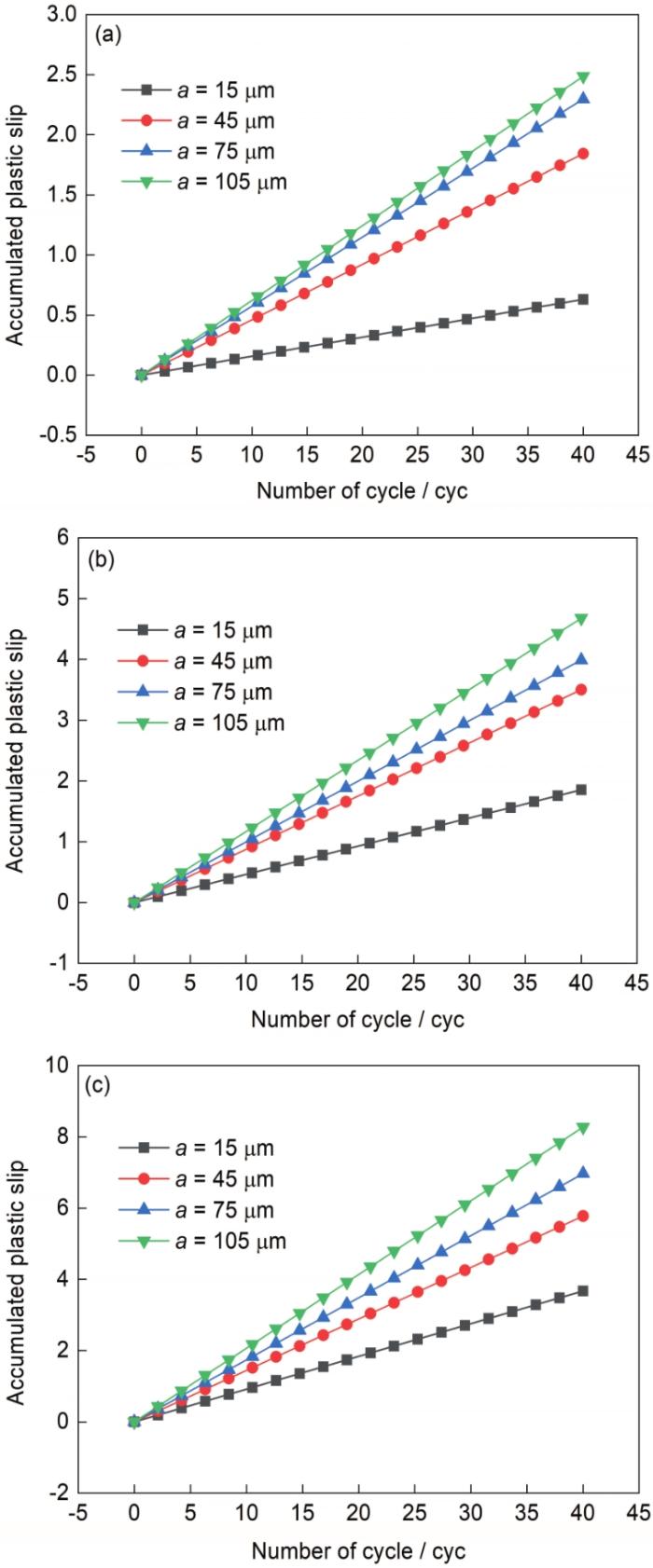
图8 累积塑性滑移与循环周次间的关系
Fig.8 Relationships between accumulated plastic slip and cycle number
(a)
3.1.3 寿命对比
分别基于累积能量耗散和累积塑性滑移,通过
图9
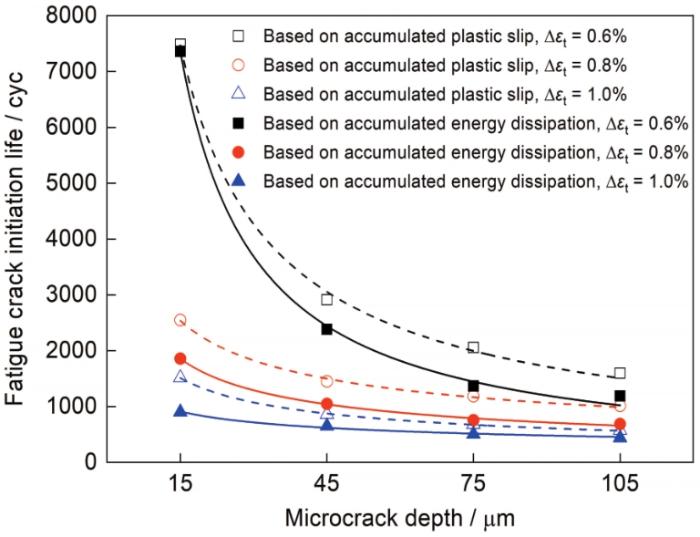
图9 基于累积能量耗散和累积塑性滑移疲劳裂纹萌生寿命预测对比
Fig.9 Comparisons of predicted fatigue crack initiation life based on accumulated energy dissipation and accumulated plastic slip
3.2 不同微缺口长度
3.2.1 累积能量耗散
应变幅为0.6%时,不同微缺口长度的模型(b = 15、45、75和105 μm)在循环10 cyc后的累积能量耗散如图10所示。由图可见,在相同的循环周次下,随着微缺口长度的不断增加,累积能量耗散不断减少,与微缺口深度变化所得趋势相反。
图10
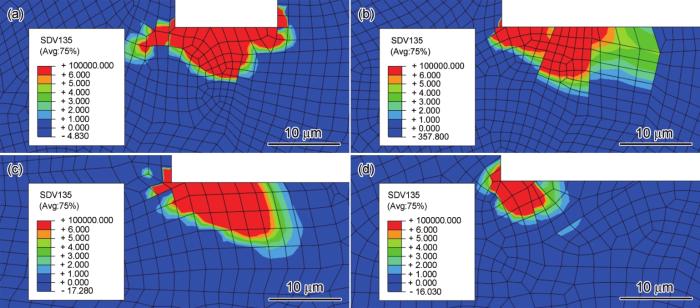
图10 应变幅为0.6%时不同微缺口长度模型在循环10 cyc后的累积能量耗散
Fig.10 Accumulated energy dissipation illustrations of models with different micro-notch lengths when
(a) b = 15 μm (b) b = 45 μm (c) b = 75 μm (d) b = 105 μm
3种应变幅下4个微缺口长度模型累积能量耗散与循环周次间的关系如图11所示。可见,与不同微缺口深度相同,对于具有特定微缺口尺寸的模型,在特定的应变幅加载下,随着循环周次的增加,累积能量耗散线性增加,能量耗散的累积速率恒定;应变幅对累积能量耗散和能量耗散累积速率的影响更大,随着应变幅增加,二者均逐渐增加。与不同微缺口深度时的情况不同,随着微缺口长度增加,能量耗散累积速率逐渐降低,且其趋于稳定的趋势不明显。如上结果可以从滞后回线的变化中得到解释。
图11
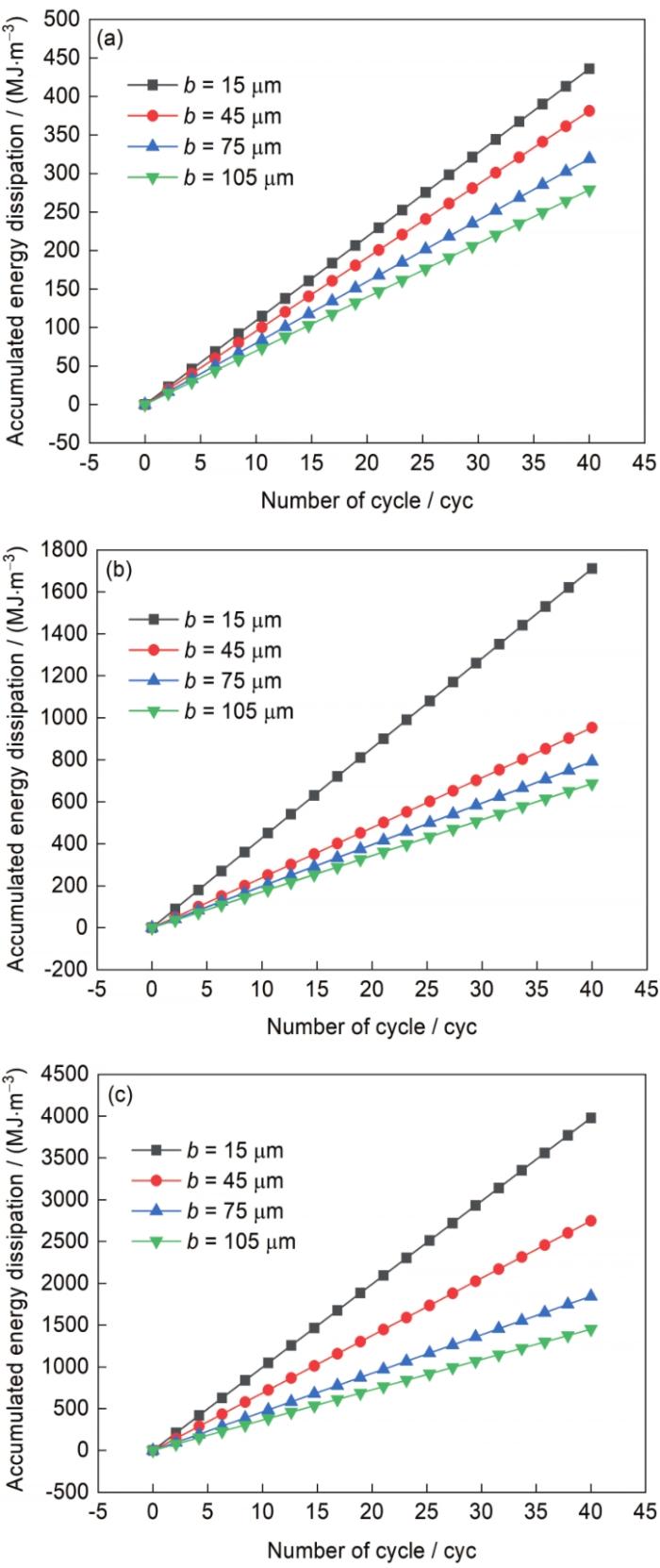
图11 累积能量耗散与循环周次间的关系
Fig.11 Relationships between accumulated energy dissipation and cycle number
(a)
微缺口左下角点在应变幅0.6%、不同微缺口长度、循环第10 cyc时的滞后回线如图12所示。可见,随着微缺口长度的增加,滞后回线的应变变化范围逐渐减小、应力变化范围基本一致(在b = 105 μm时有所降低),这与微缺口尺寸变化方向和加载方向一致有关。随着微缺口长度增加,沿加载方向应变被平均,应变变化范围均匀减小,应力变化范围基本不变。
图12

图12 应变幅0.6%时微缺口左下角点在循环第10 cyc后的滞后回线
Fig.12 Hysteresis loops of the point at the lower left corner of the micro-notch at
3.2.2 累积塑性滑移
应变幅为0.6%时,4个微缺口长度模型在循环10 cyc后的累积塑性滑移如图13所示。可见,与累积能量耗散规律一致,在相同的循环周次下,随着微缺口长度的不断增加,累积塑性滑移不断减少。
图13
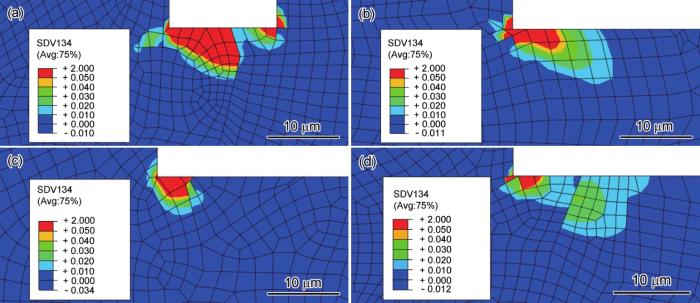
图13 应变幅为0.6%时不同微缺口长度模型在循环10 cyc后的累积塑性滑移
Fig.13 Accumulated plastic slip illustrations of models with different micro-notch lengths when
(a) a = 15 μm (b) a = 45 μm (c) a = 75 μm (d) a = 105 μm
不同应变幅下,不同微缺口长度模型累积塑性滑移与循环周次间的关系如图14所示。可见,累积塑性滑移与循环周次同样呈线性关系,塑性滑移的累积速率同样恒定。且随着微缺口长度的增加,塑性滑移的累积速率逐渐降低。应变幅的增加同样会显著提高累积塑性滑移和塑性滑移累积速率。
图14
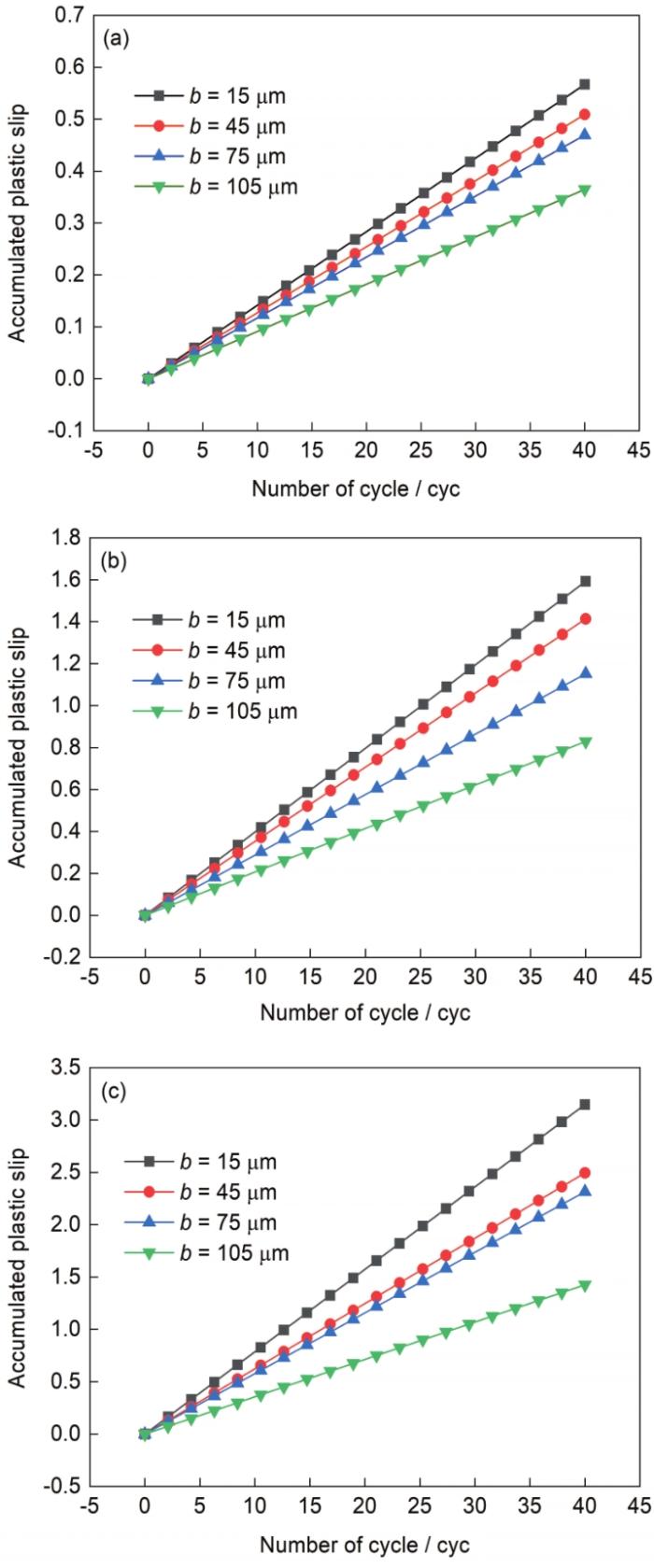
图14 累积塑性滑移与循环周次间的关系
Fig.14 Relationships between accumulated plastic slip and cycle number
(a)
3.2.3 寿命对比
分别基于累积能量耗散和累积塑性滑移计算得到不同微缺口长度、不同应变幅下的疲劳裂纹萌生寿命,如图15所示。与3.1.3节相同,在寿命计算时,为方便起见,分别用能量耗散和塑性滑移的累积速率代替Wcyc和Pcyc。由图可见,随着微缺口长度的增加,疲劳裂纹萌生寿命逐渐增加;随着应变幅的增加,疲劳裂纹萌生寿命显著降低。基于累积塑性滑移和累积能量耗散进行预测所得寿命相差不大。
图15
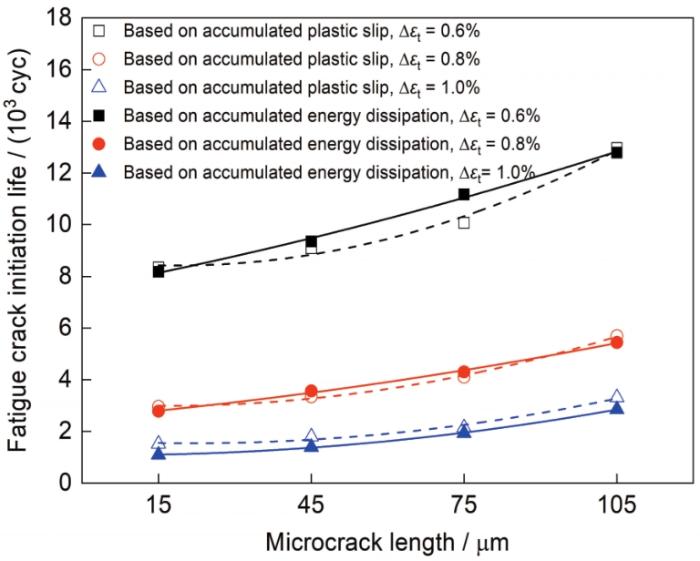
图15 基于累积能量耗散和累积塑性滑移疲劳裂纹萌生寿命预测对比
Fig.15 Comparisons of predicted fatigue crack initiation life based on accumulated energy dissipation and accumulated plastic slip
4 疲劳裂纹萌生寿命与拘束间的关联
可以发现,在不同的微缺口深度和长度(拘束)下,疲劳裂纹萌生寿命有很大的不同。为了对含缺口试样或结构进行准确的结构完整性评价,需建立疲劳裂纹萌生寿命与拘束间的关联,在评价中纳入拘束效应的影响。
图16
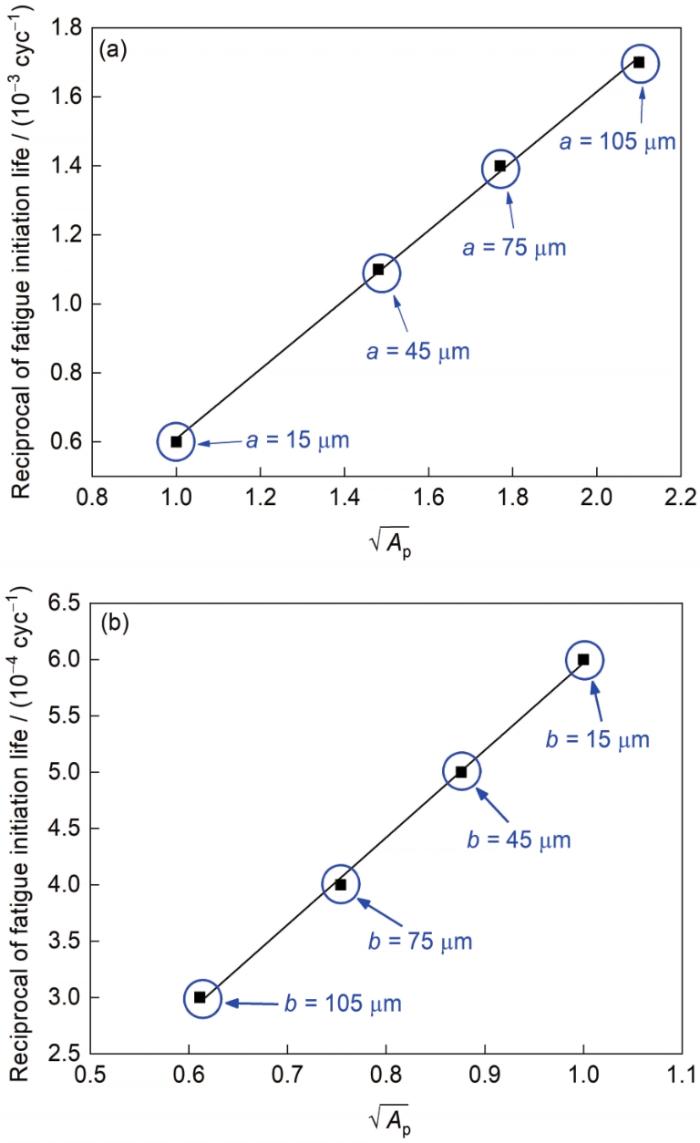
图16 疲劳裂纹萌生寿命与拘束间的关联
Fig.16 Relationships between fatigue crack initiation life and constraint
(a) different micro-notch depth
(b) different micro-notch length
图17
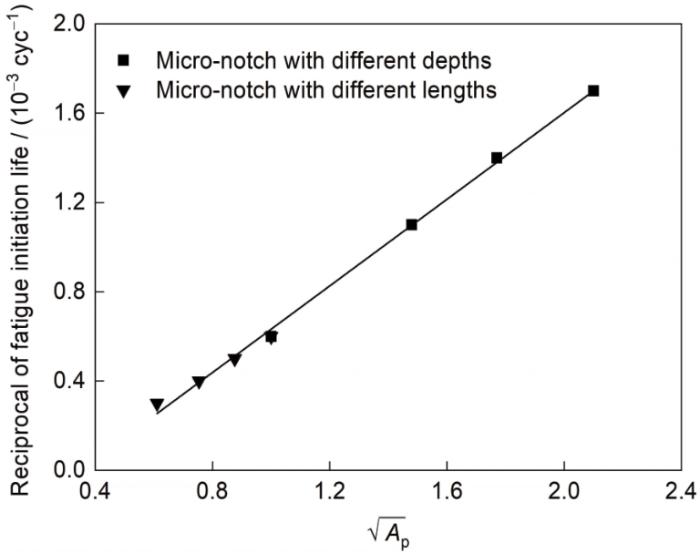
图17 所有模型疲劳裂纹萌生寿命与拘束间的关联
Fig.17 Relationship between fatigue crack initiation life and constraint of all models
这进一步表明Ap可以适用于疲劳领域,可以将其应用范围从准静态加载推广到疲劳加载。另一方面,结果表明疲劳裂纹萌生寿命在很大程度上取决于等效塑性应变等值线所围绕区域的面积。在之前的研究中,Chikh等[43]试图将塑性区尺寸作为一个力学参数引入疲劳裂纹失效准则,然而所使用的塑性区尺寸多指塑性区的长度,并非面积。从本工作结果来看,等效塑性应变等值线所围绕区域的面积或许可以作为一个合适的参数引入疲劳裂纹失效准则。此外,疲劳裂纹萌生寿命与
5 结论
(1) 随着微缺口深度的增加,能量耗散和塑性滑移的累积速率逐渐加快,累积能量耗散和累积塑性滑移逐渐增加,疲劳裂纹萌生寿命减少;随着微缺口长度的增加,变化趋势相反。这与微缺口尺寸变化方向和加载方向有关。
(2) 与微缺口深度和长度的改变相比,应变幅改变所带来的影响更大。随着应变幅的增加,累积能量耗散和累积塑性滑移均显著增加,疲劳裂纹萌生寿命显著减少。
(3) 在不同微缺口深度下,基于累积能量耗散进行预测所得寿命比基于累积塑性滑移进行预测所得寿命略低;在不同微缺口长度下,基于累积能量耗散和基于累积塑性滑移进行预测所得寿命相差不大。
(4) 在不同的微缺口深度和长度下,疲劳裂纹萌生寿命均与







 沪公网安备31011202020290号
沪公网安备31011202020290号
