分享：基于不同失稳理论的 DP780双相钢成形极限预测

摘 要:采用板材综合成形试验机对 DP780双相钢进行极限应变试验,分别基于 C-H 失稳理 论和 M-K 凹槽失稳理论搭载 Yld2000屈服准则和幂指数硬化模型对 DP780双相钢成形极限曲线 进行预测,并与试验结果进行对比。结果表明:基于 M-K 凹槽失稳理论和 C-H 失稳理论获得的成 形极限曲线对成形极限的预测精度分别为97.97%和95.82%;初始厚度不均匀度越大,钢板表面 越光滑,越有利于成形;当初始厚度不均匀度为0.992时,M-K 凹槽失稳理论对 DP780双相钢成形 极限的预测精度最高,相对误差为0.66%,在实际冲压生产中,当初始厚度不均匀度取0.992时,该 理论模型可作为获取 DP780双相钢成形极限曲线的一种可靠方法。 

关键词:双相高强钢;成形极限;失稳理论;初始厚度不均匀度 

中图分类号:TG381 文献标志码:A 文章编号:1000-3738(2022)05-0082-06

0 引 言 

近年来,汽车轻量化逐渐成为了汽车制造领域 的热点话题,而双相高强钢的广泛应用是实现汽车 轻量化的有效途径之一[1]。目前,DP780双相高强 钢在汽车上的使用越来越多;有关 DP780双相钢成 形极限的研究具有重要意义。成形极限是描述材料 变形能力的重要工艺参数和性能指标,其揭示了材 料在集中性失稳前的最大变形程度[2-3]。在预测成 形极限的方法中,通过失稳理论结合屈服准则以及 硬化模型计算的成形极限曲线是最为直观有效且广 泛 应 用 的 方 法。 目 前,常 用 的 失 稳 理 论 包 括 Considere失 稳 理 论[4]、Swfit分 散 性 失 稳 理 论[5]、 Hill集中性失稳理论[6]、M-K 凹槽失稳理论[7]和 CH 失稳理论[8]等,其中 M-K 凹槽失稳理论和 C-H 失稳 理 论 应 用 最 为 广 泛。 M-K 失 稳 理 论 是 由 Marciniak和 Kuczynski提出的,其核心是假设材料表面在与最大主应力垂直的方向上存在初始厚度不 均匀度[7]。C-H 失稳理论是由陈光南教授提出的, 也称平面应变漂移失稳准则;该理论认为大多数板 材的表面缺陷不会导致应变集中,导致板材发生集 中性失稳的主要因素为内部孔穴的尺寸与分布[8]。 已有许多学者针对板材的成形极限开展了广泛研 究。蔡旺等[9]将 M-K 失稳理论和耦合晶体塑性本 构关系相结合,建立了预测 TWIP590钢板塑性变 形的有限元模型,同时分析了初始织构、初始厚度不 均匀度和初始凹槽角度对成形极限的影响,发现初 始织构为铜型织构的成形性能较好,随初始厚度不 均匀度增大、初始凹槽角度减小,成形极限应变增 大。杜平梅等[10]基于 M-K 凹槽失稳理论结合常温 和高温下的修正Swift本构模型绘制了成形极限理 论预测曲线,并对 TRIP780高强钢板成形极限进行 了预测,试验数据与理论预测的相对误差在10%以 内。王建勋[11]通过胀形试验的有限元仿真验证了 板材变形过程中诱发厚向应力的存在,并将诱发厚 向应力引入到 C-H 失稳理论中,搭载 Hill'48屈服 准则得到成形极限预测曲线;分析了材料塑性应变 比r 值对成形极限曲线的影响,材料在变形过程中 的诱发厚向拉应力会降低r 值对成形极限曲线影响的敏感性。目前,关于材料成形极限预测的研究大 多以某一失稳理论为基础,研究模型本身参数对成 形极限的影响,而不同失稳理论对于成形极限的预 测精度不尽相同。适用的失稳理论是精确预测材料 成形极限的前提条件,也是实现其推广应用的重要 手段。为此,作者选用 C-H 失稳理论和 M-K 凹槽 失稳理论,结合 Yld2000屈服准则[12]和幂指数硬化 模型[13]预测了 DP780双相钢的成形极限曲线,并 与试验结 果 进 行 了 对 比,评 估 了 两 种 失 稳 理 论 对 DP780双相钢成形极限的预测能力。 

1 试样制备与试验方法

 试验材料选用首钢生产的厚度为1.6mm 的冷 轧 DP780双相高强钢板,采用 ARL4460型直读光谱 仪测定其化学成分,结果见表1。采用线切割法在 DP780双相钢板上截取尺寸为20 mm×20 mm× 1.6mm 的金相试样,经打磨、抛光,用体积分数4% 的硝酸酒精溶液腐蚀后,根据 GB/T13298-2015, 采用 Leicadmi5000m 型光学显微镜观察显微组织。 由图1可以看出,DP780双相钢的显微组织表现为 铁素体基体和基体中弥散分布的细小马氏体组织。 

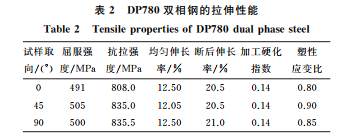
根 据GB/T228-2002,在 试 验 钢 板 上 沿 轧 制方向(0°方向)、与轧制方向成45°角方向和垂直轧制 方向(90°方向)分别截取标距为80mm 的“哑铃型” 拉伸试样,采用Zwick-Z100型万能试验机进行准静 态拉伸试验,应变速率为0.001s -1,共完成9次平 行试验并取平均值。由表2可以看出,不同加载方 向下 DP780双相钢的塑性应变比差异较大,说明其 具有显著的各向异性特性。

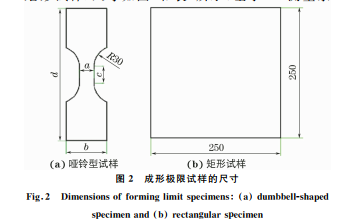
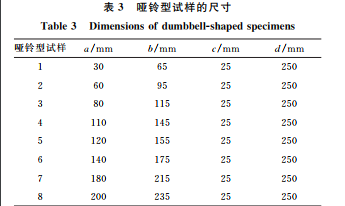
按照 GB/T15825.8-2008,采用首钢与北航合 作研发的 BSC-400型高强汽车板材综合成形试验 机进行成形极限试验,润滑剂采用二硫化钼锂基润 滑脂。DP780双相钢试样(8种哑铃型试样和1种 矩 形试样)尺寸如图2和表3所示,基于DIC测量系统完成应变的采集。成形极限试验后试样的宏观形 貌如图3所示。 

2 成形极限预测 

2.1 Yld2000屈服准则和幂指数硬化模型 

在预测材料成形极限的方法中,基于失稳理论 结合屈服准则以及硬化模型预测成形极限是最为有 效的方法。在主应力空间下,Yld2000屈服准则[12] 的表达式为σ- =[(c1σ1 +c2σ2 m + c3σ1 +c4σ2 m + c5σ1 +c6σ2 m )]1/m (1) c1 =L'11 -L'21 (2) c2 =L'12 -L'22 (3) c3 =2L″21 +L″11 (4) c4 =2L″22 +L″12 (5) c5 =2L″11 +L″21 (6) c6 =2L″12 +L″22 (7) L'11 L'12 L'21 L'22 L'66 ?? ?? ???????????????? ?? ?? ???????????????? = 2/3 0 0 -1/3 0 0 0 -1/3 0 0 2/3 0 0 0 1 ?? ?? ?????????????? ?? ?? ?????????????? · α1 α2 α7 ?? ?? ???????? ?? ?? ???????? (8) L″11 L″12 L″21 L″22 L″66 ?? ?? ???????????????? ?? ?? ???????????????? = 1 9 -2 2 8 -2 0 1 -4 -4 4 0 4 -4 -4 1 0 -2 8 2 -2 0 0 0 0 0 9 ?? ?? ?????????????? ?? ?? ?????????????? α3 α4 α5 α6 α8 ?? ?? ???????????????? ?? ?? ???????????????? (9) 式中:σ- 为等效应力;σ1 和σ2 分别为第一、第二主应 力;m,α1 ~α8 为材料参数;C1 ~C6 为由α1 ~α8 计 算得到的中间参数。 令应力比α=σ2/σ1,并设ψ=σ-/σ1,代入式(1) 中得: ψ=[(c1 +c2α m + c3 +c4α m + c5 +c6α)m )/2]1/m (10) 式中:α为第一主应力与第二主应力之比;ψ为等效 应力与第一主应力之比。 

幂指数硬化模型[13]的表达式为 σ- =K·ε-b (11) 式中:K 为材料强度系数;b 为硬化指数;ε- 为等效 塑性应变。 基于幂指数硬化模型,采用 First-OPT 软件对 DP780双相钢沿轧制方向的流动应力-应变曲线进行拟合,得到强度系数为1289,硬化指数为0.1489。根 据文献[12]中 Yld2000屈服准则的材料参数求解方 法,求得的材料参数列于表4。 

2.2 基于C-H失稳理论的成形极限预测

 C-H 失稳准则认为板料拉伸集中性失稳是一个 渐进过程,该过程的起点是分散性失稳,损伤的主要 贡献不是损伤量的变化而是其导致了板料应变状态 的漂移,这一过程的终点是宏观平面应变状态的实 现[8]。基于C-H 失稳理论结合 Yld2000屈服准则和 幂指数硬化模型的成形极限预测计算过程如下。 

材料稳定变形时,变形抗力等于应力增量,则有: b ε- ·σ-·dε- =ψ 1- αψ1 ψ m dσ1 +ψ 1-mψ1dσ2 (12) ψ={(c1 +c2α m + c3 +c4α m + c5 +c6α m )/2}1/m (13) ψ1 =(c2 c1 +c2α m-1 +c4 c3 +c4α m-1 + c6 c5 +c6α m-1)/2 (14) 式中:ψ1 为由α 和α1~α8 计算得到的中间变量。 若对板料进行比例加载,即α 为常数,可求得分 散性失稳阶段的极限应变为 ε1d = bψψ2 ψψ2(1-αψ1/ψ m )-ψ 2 1αψ 1-m (15) ε2d = bψψ1 ψψ2(1-αψ1/ψ m )-ψ 2 1αψ 1-m (16)ψ2 =(c1 c1 +c2α m-1 +c3 c3 +c4α m-1 + c5 c5 +c6α m-1)/2 (17) 式中:ε1d,ε2d 分别为分散性失稳阶段的第一和第二 主应变;ψ2 为由α和α1 ~α8 计算得到的中间变量。 根据C-H 失稳理论,当载荷在最大水平保持恒定 时,应变路径开始向平面应变状态漂移,即次应变逐渐 趋近于0,此时板料产生集中性失稳[8],表达式为dσ2 = ψ ψ 1-mψ1 b ε- - (ψ-αψψ1/ψ m )ψ2 ψ m ?? ?? ???? ?? ?? ???? σ1dε- (18) dσ1 =σ1dε1 = ψ2 ψ m-1σ1dε- (19) 式中:ε1 为第一主应变。 

在漂移 阶 段 用 迭 代 法 逐 步 积 分 式 (18)和 式 (19),即 可 求 出 集 中 性 失 稳 时 的 极 限 应 变 值。若 dε2 无限趋近于0(指定截断误差 dε2 ≤0.00001), 则终止运算,输出集中性失稳时的极限应变值为 ε * 1n =ε1d + ∑ N-1 i=1 dε1 (20) ε * 2n =ε2d + ∑ N-1 i=1 dε2 (21)

式中:ε2 为第二主应变;ε * 1n 和ε * 2n 分别为集中性失 稳时第 一 和 第 二 主 应 变 极 限 应 变 值;N 为 迭 代 次数。

2.3 基于 M-K 凹槽失稳理论的成形极限预测 

M-K 理论失稳理论模型如图4所示,该理论认 为板料表面粗糙度不一,存在较为薄弱的环节,即为 “凹槽”(图中b区),据此假设其表面在与最大主应 力垂直的方向上存在初始厚度不均匀度[7]。

在 M-K 凹槽失稳理论中,须满足 4 个必要条 件,即变形连续性条件、载荷平衡条件、能量守恒及 虚功原理条件、体积不变原理条件[14],每个必要条 件对应的不同平衡方程如下。

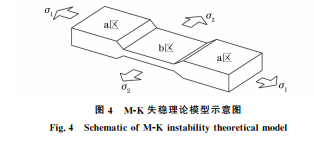
变形连续性条件,即非凹槽区(图4中a区)和 凹槽区(图4中b区)的第一主应变增量值相等,其 几何协调方程为 dε1a =dε1b (22) 式中:ε1a 为a区第一主应变;ε1b 为b区第一主应变。 载荷平衡条件,即平行凹槽方向与垂直凹槽方 向上,非凹槽区与凹槽区的载荷相等,其平衡方程为 taσ2a =tbσ2b (23) taσ3a =tbσ3b (24) 式中:σ2a 和σ2b 分别为a区和 b区的第二主应力; σ3a 和σ3b 分别为a区和b区的第三主应力;ta 和tb 分别为a区和b区的板材厚度。 

根据能量守恒及虚功原理条件可以得到: σ-dε- =σ2dε2 +σ1dε1 (25) 在平面应力状态下材料塑性变形满足体积不变原理条件,金属板料厚度方向的应变ε3 可表示为 dε3 =-dε1 -dε2 (26) 材料变形过程中瞬时厚度f 的表达式为 f=ta/tb =f0·exp ε3b -ε3a (27) 式中:f0 为初始厚度不均匀度;ε3a 和ε3b 分别为a区 和b区的第三主应变。 根据上述4个平衡方程,将图4中的a区和b区 联系起来,可得: σ-a φ a·exp(ε3a)=f0· σ-b φ b·exp(ε3b) (28) 式中:σ-a 和σ-b 分别为a区和b区 Yld2000屈服准则代表 的 等 效 应 力;φ a 和 φ b 分 别 为 a 区 和 b 区 Yld2000屈服准则代表的等效 应 力 与 第 一 主 应 力 的比。 

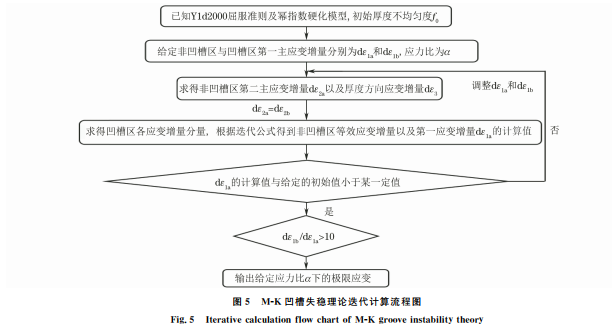
根据上述平衡方程,结合 Yld2000屈服准则和幂 指数硬化模型以及给定的非凹槽区和凹槽区第一主 应变增量dε1a,dε1b 和应力比α,即可计算求得凹槽区 的应力以及应变增量。采用 Newton-Raphson数值迭 代法[14]对式(28)进行迭代计算,获得应力比α下的极 限应变,迭代流程如图5所示。选取不同 的α 取值 (0≤α ≤1),重复迭代计算,即可求得不同应力比 下材料的极限应变,从而绘出成形极限曲线。

3 成形极限曲线 

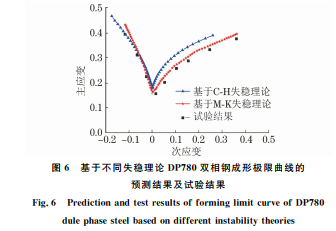
分别基于 C-H 失稳理论和 M-K 凹槽失稳理论 对 DP780双相钢的成形极限曲线进行预测,并与试 验结果进行对比。由图6可以看出:基于两种失稳 理论预测的成形极限曲线变化趋势与试验结果基本 一致;基于 C-H 失稳理论预测的成形极限曲线与成 形极限曲线左侧(单向拉伸)区域的试验结果吻合度 较高,但其高估了 DP780双相钢在单向拉伸加载状 态下的极限应变,同时对于成形极限曲线右侧(双向 等拉)区 域 的 预 测 精 度 较 差,整 体 预 测 精 度 为 95.82%;基于 M-K 凹槽失稳理论预测的成形极限 曲线与试验结果整体吻合效果明显优于基于 C-H 失稳理论,但对于成形极限曲线右侧区域的预测仍 存在一定误差,整体预测精度为97.97%。为此,后 续开展了 M-K 凹槽失稳理论中初始厚度不均匀度 对成形极限的影响研究。

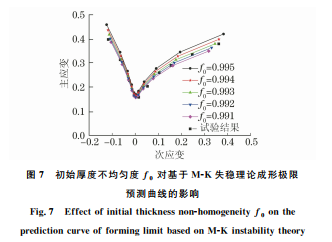
初始厚度不均匀度f0 是 M-K 凹槽失稳理论 中的重要参数,对成形极限结果具有重要影响[15]。 由图7可知:随着f0 的增大,成形极限曲线最低点 会随之提高,即平面应变点的极限应变增大,成形 极限曲线整体呈上升趋势,说明f0 越大,材料表 面越光滑,能达到更大的塑性变形;同时,随着f0的减小,成形极限曲线左右两部分缩短,即对于单 向拉伸和双向等拉两种加载状态下的极限应变预 测精度均变低。将不同初始厚度不均匀度下预测 的成形极限 曲 线 与 试 验 结 果 进 行 对 比 后 发 现,当 f0 = 0.992时,基于 M-K 凹槽失稳理论获得的成 形极限 曲 线 预 测 精 度 最 高,相 对 误 差 为 0.66%。 实际工 程 应 用 中,采 用 M-K 凹 槽 失 稳 理 论 预 测 DP780双相钢 成 形 极 限 时,建 议 初 始 厚 度 不 均 匀 度取为0.992。 

4 结 论 

(1)结合 Yld2000屈服 准 则 和 幂 指 数 硬 化 模 型,基于 C-H 失 稳 理 论 和 M-K 凹 槽 失 稳 理 论 对 DP780双相钢 的 成 形 极 限 曲 线 进 行 预 测,预 测 精 度分别为97.97%和95.82%,基于 M-K 凹槽失稳 理论预测的成形极限理论曲线与试验结果吻合度 更高。 (2)基于 M-K 凹槽失稳理论预测 DP780双相 钢的成形极限时,钢板的初始厚度不均匀度越大,钢 板表面越光滑,越有利于成形;当初始厚度不均匀度 为0.992时,M-K 凹槽失稳理论对 DP780双相钢成 形极限的预测精度最高,相对误差为0.66%,该理 论模型可作为获取 DP780双相钢成形极限曲线的 一种可靠方法。

参考文献: 

[1] 李小强,董红 瑞,于 长 旺,等.不 同 屈 服 准 则 与 硬 化 模 型 对 DP780双相高强钢拉延弯曲回弹预测影响规律研究[J].机械 工程学报,2020,56(12):42-55. LIXQ,DONG H R,YUC W,etal.Influenceofyieldcriteria andhardeningmodelondraw-bendingspringbackpredictionof DP780[J].JournalofMechanicalEngineering,2020,56(12): 42-55. [2] CHAIMONGKON T,PANICH S,UTHAISANGSUK V. Anisotropicfractureforminglimitcurveanditsapplicationsfor sheetmetalforming withcomplexstrainpathsofaluminum sheet [J ]. The International Journal of Advanced ManufacturingTechnology,2021,115(11/12):3553-3577. [3] PANDRES,MORCHHALEA,MAHALLEG,etal.Fracture limitanalysisofDP590steelusingsinglepointincremental forming:Experimental approach,theoretical modeling and microstructuralevolution[J].ArchivesofCivilandMechanical Engineering,2021,21(3):1-20. [4] CONSIDERE M. L'emoploi du fer et I'acier dans les constructions[J].AnnalesDesPontserChausse'es,1885,9 (6):574-574. [5] SWIFT H W.Plasticinstabilityunderplanestress[J].Journal oftheMechanicsandPhysicsofSolids,1952,1(1):1-18. [6] HILLR.Ondiscontinuousplasticstates,withspecialreference tolocalizedneckinginthinsheets[J].JournaloftheMechanics andPhysicsofSolids,1952,1(1):19-30. [7] MARCINIAK Z,KUCZY'NSKI K.Limit strains in the processesofstretch-forming sheet metal[J].International JournalofMechanicalSciences,1967,9(9):609-620. [8] 陈光南.板料拉伸变形损伤、失稳与成形极限研究[D].北京: 北京航空航天大学,1991. CHEN G N.Research on sheet metaltensile deformation damage,instabilityandforminglimit[D].Beijing:Beihang University,1991. [9] 蔡旺,钱凌云,孙朝阳,等.基于 CPFE-MK 模型的 TWIP钢板 成形极限预测[J].塑性工程学报,2021,28(6):53-60. CAIW,QIANLY,SUNCY,etal.Predictionofforminglimit ofTWIPsteelsheetbasedonCPFE-MK model[J].Journalof PlasticityEngineering,2021,28(6):53-60. [10] 杜平梅,郎利辉,刘宝胜,等.基于 M-K 模型的成形极限预测 及参数影响[J].塑性工程学报,2011,18(5):84-89. DUP M,LANG L H,LIU BS,etal.Theoreticalprediction andparameterinfluenceofFLDsbasedon M-K model[J]. JournalofPlasticityEngineering,2011,18(5):84-89. [11] 王建勋.涉及厚向应力的板料成形极限研究[D].北京:北方 工业大学,2019. WANGJX.Theinvestigationonforminglimitofsheetmetal involving thickness stress [D ].Beijing:North China UniversityofTechnology,2019. [12] 王海波.复杂加载路径下板料屈服强化行为及成形极限研究 [D].北京:北京航空航天大学,2009. WANG H B.Yieldingandhardeningbehaviorandforming limitforsheet metalundercomplexloading paths[D]. Beijing:BeihangUniversity,2009. [13] LIXQ,DONG H R,WANG H B,etal.Effectofstrainrate differencebetweeninsideandoutsidegrooveinM-Kmodelon predictionofforminglimitcurveof Ti6Al4V atelevated temperatures[J].TransactionsofNonferrousMetalsSociety ofChina,2020,30(2):405-416. steelat650℃[J].EngineeringFractureMechanics,2017,175: 57-71. [3] ZHANGSL,XUAN FZ.Interactionofcyclicsofteningand stressrelaxationof9%-12% Crsteelunderstrain-controlled fatigue-creep condition:Experimental and modeling [J]. InternationalJournalofPlasticity,2017,98:45-64. [4] JID M,REN JX,ZHANG L C.A novelcreep-fatiguelife prediction modelforP92steelonthebasisofcyclicstrain energy density[J].Journal of Materials Engineering and Performance,2016,25(11):4868-4874. [5] SAINI N,PANDEY C,MAHAPATRA M M,et al.A comparativestudy ofductile-brittletransition behaviorand fractographyofP91and P92steel[J].Engineering Failure Analysis,2017,81:245-253. [6] JIDM,ZHANGLC,RENJX,etal.Creep-fatigueinteraction andcyclicstrainanalysisinP92steelbasedontest[J].Journal ofMaterialsEngineeringandPerformance,2015,24(4):1441- 1451. [7] JID M,SHEN M H H,WANG DX,etal.Creep-fatiguelife predictionandreliabilityanalysisofP91steelbasedonapplied mechanicalworkdensity[J].JournalofMaterialsEngineering andPerformance,2015,24(1):194-201. [8] SKLENICKA V,KUCHAROVA K,SVOBODOVA M,etal. Theeffectofapriorshort-termageingonmechanicalandcreep propertiesofP92steel[J].MaterialsCharacterization,2018, 136:388-397. [9] BARBADIKAR D R,DESHMUKH G S,MADDIL,etal. Effect of normalizing and tempering temperatures on microstructureand mechanicalpropertiesofP92steel[J]. InternationalJournalofPressure Vesselsand Piping,2015, 132/133:97-105. [10] ALANG N A,DAVIES C M,NIKBIN K M.Low cycle fatigue behaviour of ex-service P92 steel at elevated temperature[J].ProcediaStructuralIntegrity,2016,2:3177- 3184. [11] WANG X W,ZHANG W,GONG J M,etal.Low cycle fatigueandcreepfatigueinteractionbehaviorof9Cr-0.5Mo[8] SKLENICKA V,KUCHAROVA K,SVOBODOVA M,etal. Theeffectofapriorshort-termageingonmechanicalandcreep propertiesofP92steel[J].MaterialsCharacterization,2018, 136:388-397. [9] BARBADIKAR D R,DESHMUKH G S,MADDIL,etal. Effect of normalizing and tempering temperatures on microstructureand mechanicalpropertiesofP92steel[J]. InternationalJournalofPressure Vesselsand Piping,2015, 132/133:97-105. [10] ALANG N A,DAVIES C M,NIKBIN K M.Low cycle fatigue behaviour of ex-service P92 steel at elevated temperature[J].ProcediaStructuralIntegrity,2016,2:3177- 3184. [11] WANG X W,ZHANG W,GONG J M,etal.Low cycle fatigueandcreepfatigueinteractionbehaviorof9Cr-0.5Mo[17] DUNDU M.Evolution ofstress-strain modelsofstainless steelinstructuralengineeringapplications[J].Construction andBuildingMaterials,2018,165:413-423. [18] SONGB,SANBORN B.Relationshipofcompressivestressstrainresponseofengineeringmaterialsobtainedatconstant engineeringandtruestrainrates[J].InternationalJournalof ImpactEngineering,2018,119:40-44. [19] CAIW Y,MOROVAT M A,ENGELHARDT M D.True stress-strain curves for ASTM A992 steel for fracture simulation at elevated temperatures [J].Journal of ConstructionalSteelResearch,2017,139:272-279. [20] 葛仁跃.基于损 伤 演 化 机 理 的 P92 钢 蠕 变-疲 劳 试 验 研 究 [D].杭州:浙江工业大学,2020. GE R Y.Creep-FatiguetestofP92steelbasedondamage evolutionmechanism[D].Hangzhou:ZhejiangUniversityof Technology,2020.