分享：颗粒增强金属基复合材料细观有限元建模方法的对比

摘 要:以原位生成法制备的 TiB2 颗粒增强铁基复合材料为研究对象,通过纳米压痕试验及有 限元反演分析确定基体的幂硬化模型参数,建立二维细观真实结构模型和颗粒随机分布的体胞模 型,然后模拟单轴拉伸试验,用等效宏观方法计算真应力-真应变曲线,对2种模型的模拟结果进行 对比,并探讨边界条件对模拟结果的影响。结果表明:边界条件对模拟单轴拉伸时的真应力-真应 变曲线影响较小;2种模型模拟得到单轴拉伸的真应力-真应变曲线差异较小,且与试验结果吻合, 相对误差小于5%;真实结构模型模拟得到的弹性模量与屈服强度的误差小于体胞模型;不同模型 模拟得到基体与颗粒的局部微观等效应力场及应变场有明显差异。

关键词:颗粒增强复合材料;细观模型;有限元模拟;应力-应变曲线

中图分类号:TG148 文献标志码:A 文章编号:1000-3738(2022)04-0082-07

0 引 言 

颗粒增强金属基复合材料具有较高的强度、弹 性模量、硬度以及良好的塑性,并且生产成本低廉, 应用前景广泛。颗粒增强金属基复合材料在承受载 荷时的变形与失效等行为是非常复杂的,与基体和 颗粒两相材料的性能以及二者之间的多种相互作用 密切相关。在研究微观及细观结构对复合材料力学 性能的影响中,采用有限元方法进行数值模拟是一 种非常有效的手段。想要进行有效的模拟,必须先要建立合理的细观有限元模型。目前,颗粒增强复 合材料的细观有限元模型主要有体胞模型和真实结 构模型2种。体胞模型的构建基于复合材料的结构 特征,可分为单颗粒模型及多颗粒模型[1-2]。单颗粒 模型由于其结构简单,常用其来揭示基体、颗粒及界 面之间的作用机理,但无法探究颗粒之间的相互关 系[3]。对于多颗粒模型,可以假设颗粒是均匀分布 的,也可以使用随机序列吸附法生成随机分布多颗粒 模型[4]。随机分布多颗粒模型相比于单颗粒模型虽 然考虑了颗粒间的相互作用,并且一定程度上考虑了 材料的不均匀性,但与复合材料的真实微观结构还有 一定差异[5]。研究[6]表明,颗粒形貌越接近实际情 况,模拟结果与试验结果的误差越小,因此有学者发 展了基于材料真实显微图像的建模方式,即真实结构 模型。真实结构模型一般使用连续切片法建立,其原 理是将试样分成很多层,取得每一层的平面结构图像 并输入计算机中,然后利用三维重构技术,还原出试 样的三维真实结构[7]。由于三维真实结构模型的建 立需要复杂的前期工作并且伴随着庞大的计算量,因 此有不少学者建立了二维真实结构模型进行模拟,得 到的模拟结果与试验结果吻合得较好[8-11]。 体胞模型和真实结构模型各有特点,在模拟颗 粒增强复合材料的力学行为时得到的结果也有差 异,为了探究这2种模型的异同及特点,作者以原位 生成法制备的 TiB2 颗粒增强铁基复合材料为研究 对象,通过纳米压痕试验及有限元反演分析确定了 铁素体基体的幂硬化模型参数,建立了二维的颗粒 随机分布的体胞模型和真实结构模型,模拟材料在 单轴拉伸时的力学行为,研究了2种模型有限元模 拟结果的异同,并进一步探究了边界条件对模拟结 果的影响,以期在一定程度上为颗粒增强铁基复合 材料微观结构的优化设计提供参考。 

1 有限元模型的建立 

1.1 材料参数的确定

在有限元建模的过程中,需要输入复合材料各 相的材料参数。在采用原位生成的方法制备的 TiB2 颗粒增强铁基复合材料中,铁素体晶粒尺寸与纯铁中 的铁素 体 晶 粒 尺 寸 不 同,而 且 晶 粒 中 会 有 位 错 产 生[12],这导致复合材料中的铁素体与纯铁中的铁素 体在未受载时的初始状态可能会有较大不同。若采 用纯铁进行单轴拉伸试验来获得复合材料铁素体基 体的参数不合理,因此采用纳米压痕和有限元反演分 析的方式获得铁素体基体的材料属性。将 TiB2 颗粒 视为弹性体,弹性模量为510GPa,泊松比为0.25。对 TiB2 颗粒增强铁基复合材料进行纳米压痕试验,测 得基体的弹性模量为214GPa,硬度为4.01GPa,然后 进一步采用 DAO 等[13]推导的量纲函数及有限元反 演分析,确定基体的单轴幂率硬化应力-应变响应曲 线。假设基体的应力σ、应变ε满足以下关系: σ= Eε (σ ≤σy) σy 1+σEyεp n (σ >σy) ?????? (1) εr = σrEεn-1 y n1 -εy (2) 式中:E 为基体的弹性模量;σy,εy 分别为名义屈服 强度与对应的名义屈服应变;εp 为总应变减去名义 屈服应变;n 为幂硬化指数;σr、εr 分别为特征应力 与特征应变。

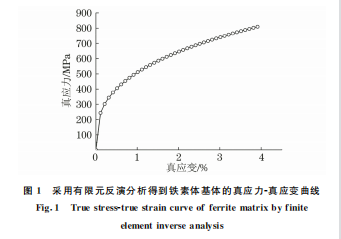
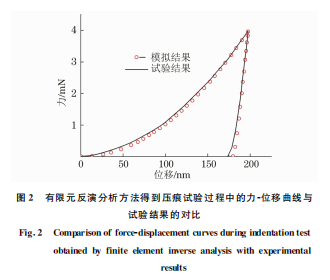
将纳米压痕试验中采用的 Berkvich压头等效 成140.6°的圆锥压头,建立轴对称纳米压痕有限元 模型[14]。参考 ANTUNES等[15]和 LEE 等[16]的研 究方法进行有限元反演,得到铁素体基体的单轴真 应力-真应变曲线如图1所示,铁素体基体的幂硬化 指数n 为0.34,屈服强度σy 为242.91 MPa,且由图 2可以看出,采用有限元反演分析方法得到压痕试 验过程中的力-位移曲线与试验结果相吻合,验证了 有限元反演分析方法的准确性。

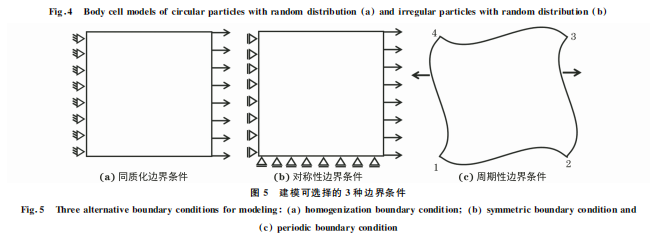
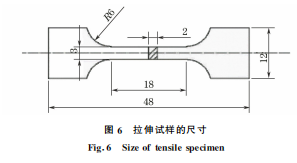
对体积分数20% TiB2 颗粒增强铁基复合材料 建立二维代表性体积元模型。研究[11]表明,当所选 取的代表性体积元尺寸大于某一临界值时,其所代 表的微结构能够反映材料微观组织的基本信息。所 选取的真实结构模型尺寸为 80μm×80μm。在 复 合 材 料 的 扫 描 电 镜(SEM)形 貌 中 选 择 尺 寸 为80μm×80μm 合适区域,经二值化处理转化为矢 量文件,然后导入 ABAQUS软件中进行建模,实现 基于微观组织的有限元模型的建立,如图3所示。 测得所选区域真实颗粒的平均尺寸为3μm。 体胞模型代表性体积元的建立则利用 ABAQUS 软件进行二次开发,采用Python语言编写程序,运行 程序建立同等颗粒尺寸、体积分数的随机分布圆形 颗粒及不规则颗粒的体胞模型,如图4所示。 在 ABAQUS软件中进行有限元模拟,将 TiB2 颗粒设为弹性体,采用 CPS4R 单元划分网格,平均 单元尺寸为0.4μm。代表性体积元模型一般可施 加3种边界条件[17],即同质化边界条件、对称性边 界条件和周期性边界条件,如图5所示。

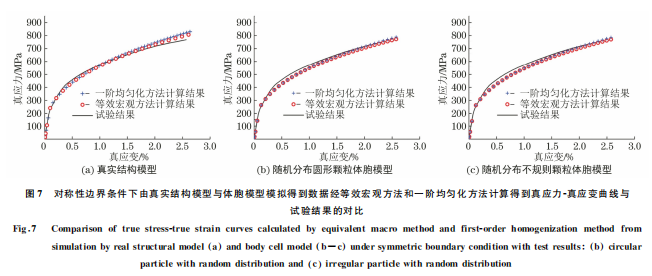
将用施加对称性边界条件的真实结构模型和体 胞模型模拟出的结果与单轴拉伸试验 结 果 进 行 对 比,结果如图7所示。由图7可以看出,采用2种 方法得到不同模型的真应力-真应变曲线与试验结 果较吻合,但 采 用 等 效 宏 观 方 法 计 算 得 到 的 真 应 力-真应变曲线与试验结果更加吻合,相对误差小 于5%,因此 后 面 采 用 等 效 宏 观 方 法 计 算 真 应 力- 真应变曲线,同 时 也 证 明 了 建 立 的 真 实 结 构 模 型 与体胞模型的合理性。 

2 结果与讨论 

2.1 边界条件对模拟结果的影响 

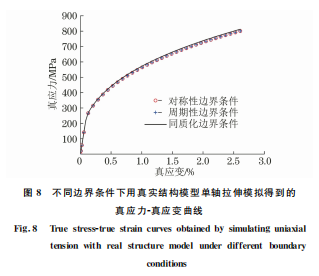
在3种边界条件下用真实结构模型进行沿水平 方向的单轴拉伸有限元模拟,得到的拉伸真应力-真 应变曲线如图8所示。由图8可以看出,不同边界 条件下模拟得到的真应力-真应变曲线基本重合,说 明边界条件对模拟结果影响较小。

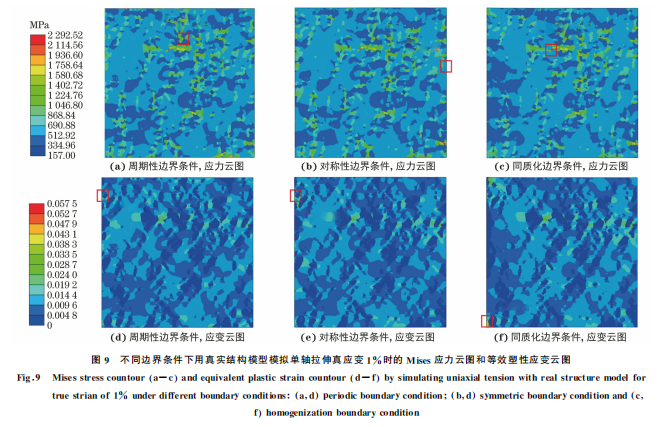
由图9可以看出,边界条件对约束位置的应力、 应变场具有一定影响,由于同质化边界条件和对称 性边界条件对垂直加载方向的约束能力弱,使模型 变形过程中沿垂直加载方向有一定的收缩,从而导 致模型的最大应力与最大等效塑性应变位置具有较 大的差异。周期性边界条件下模型变形均匀,在边 界位置应力场连续性较好,与复合材料内部实际情 况相吻合。对称性边界条件与周期性边界条件下的 应力与应变云图有较高的相似性,因此单轴拉伸试 验模拟时可用对称性边界条件代替周期性边界条件 施加载荷。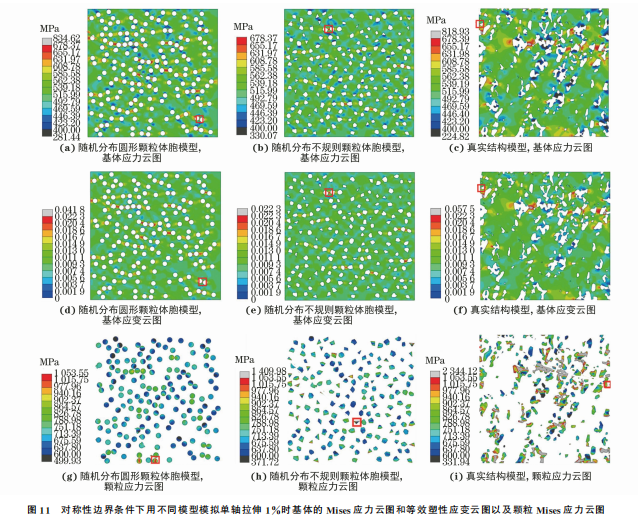

2.2 2种建模方法下模拟结果的对比 

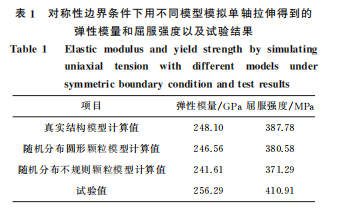
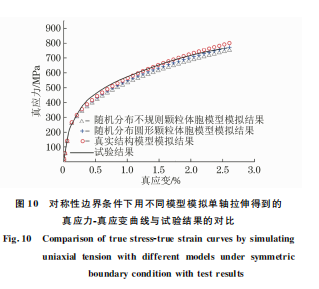
由图10可以看出,对2种模型模拟单轴拉伸得 到的真应力-真应变曲线间差异较小,且均与试验结 果吻合较好,相对误差小于5%。根据真应力-真应 变曲线计算得到的屈服强度及弹性模量如表1所示。

由表1可以看出,对2种模型模拟单轴拉伸后得到 的弹性模量及屈服强度与试验结果均相差较小,相 对误差小于10%。从工程应用的角度来看,这两种 模型都可以较好地模拟复合材料在单轴拉伸过程中 的应力-应变曲线。对真实结构模型模拟单轴拉伸 得到的弹性模量及屈服强度与试验结果间的相对误 差最小,分别为3.19%与5.63%,说明真实结构模 型在弹性模量及屈服强度模拟方面的可靠性更高。

由图11可以看出,颗粒分布与形状的不同导致 基体和颗粒的应力场和塑性应变场具有明显的差 异。体胞模型对颗粒的形状与分布进行了一定近似 处理,而真实结构模型中的颗粒具有更多的棱角, 颗粒与基体 之 间 有 较 多 的 接 触 面 积 ,因 此 相 比 于近似化的体胞模型其内部应力集中区域较多,这也是 导致真实结构模型下在相同应变时的应力略高于体 胞模型的原因。复合材料基体高应力区域多在沿加 载方向的颗粒之间,并且颗粒间距越小,其中间的基 体等效应力越大;不同模型中基体较大的等效塑性应 变主要集中在高应力区域,并且等效塑性应变云图与 各自的等效应力云图具有相似性;2种模型中颗粒的 高应力区域多位于颗粒的尖角处和颗粒间距较小处。 由表2可知:真实结构模型颗粒的最大等效应力分别 为随机分布圆形颗粒体胞模型和随机分布不规则颗 粒体胞模型的2.22倍和2.23倍;真实结构模型基体 的最大等效塑性应变分别为随机分布圆形颗粒体胞 模型和随机分布不规则颗粒体胞模型的1.38倍和2. 58倍。由此可见,2种模型模拟颗粒增强金属基复合 材料局部微观等效应力场及应变场的结果有明显差 异,这是由于在颗粒增强金属基复合材料实际服役过 程中,基体常因产生较大塑性变形而失效,而颗粒则 容易在其高应力区域的尖角处发生断裂。因此,在对 复合材料的断裂、失效等行为进行模拟时,真实结构 模型和体胞模型的模拟结果会存在较大的差异。 

3 结 论 

(1)对原位生成法制备的TiB2 颗粒增强铁基 复合材料建立了颗粒随机分布的体胞模型和真实结 构模型,采用 ABAQUS软件根据不同模型对单轴 拉伸进行有限元模拟后,采用等效宏观方法获取的 真 应力-真应变曲线与试验结果基本吻合,相对误差小于5%,验证了这2种模型的合理性。

(2)同质化边界条件、对称性边界条件和周期 性边界条件下用真实结构模型模拟拉伸得到的真应 力-真应变曲线基本重合,说明边界条件对模拟结果 影响较小;对称性边界条件下的应力与应变云图与 周期性边界条件相似,在单轴拉伸试验模拟时可用 对称性边界条件代替周期性边界条件施加载荷。

(3)用真实结构模型和体胞模型模拟单轴拉伸 得到的真应力-真应变曲线间差异较小,且均与试验 结果吻合较好,相对误差小于5%,得到的弹性模量 及屈服强度与试验结果均相差较小,相对误差小于 10%,且真实结构模型模拟单轴拉伸得到的弹性模量 与屈服强度的误差小于体胞模型,说明真实结构模型 在弹性模量及屈服强度模拟方面的可靠性更高。

(4)用不同模型模拟得到复合材料基体与颗粒 在单轴拉伸时的局部微观等效应力场及应变场有明 显差异,真实结构模型模拟颗粒的最大等效应力分 别为随机分布圆形颗粒体胞模型和随机分布不规则 颗粒体胞模型的2.22倍和2.23倍,基体的最大等 效塑性 应 变 分 别 为 这 2 种 体 胞 模 型 的 1.38 倍 和 2.58倍。

参考文献: 

[1] 陈少华.在材料研制中的连续介质细观力学有限元建模现状评 论[J].力学进展,2002,32(3):444-466. CHEN S H.Contimuum mesomechanical finite element modelingin materialsdevelopment:Astate-of-the-artreview [J].AdvancesinMechanics,2002,32(3):444-466. [2] 郑阳升,杨伟苓,郑顺奇,等.颗粒增强复合材料结构的有限元 建模研究现状[J].兵器材料科学与工程,2018,41(4):97-102. ZHENG YS,YANG W L,ZHENGSQ,etal.Researchstatus offiniteelement modelingofparticlereinforcedcomposites structure[J].Ordnance MaterialScienceand Engineering, 2018,41(4):97-102. [3] 信振洋,王悦,苗文成,等.颗粒增强金属基复合材料参数化建 模研究[J].矿业科学学报,2020,5(1):86-95. XINZY,WANGY,MIAO W C,etal.Parametricmodelingof particlereinforced metal matrixcomposites[J].Journalof MiningScienceandTechnology,2020,5(1):86-95. [4] BAILAKANAVAR M,LIU Y,FISH J,etal.Automated modelingofrandominclusioncomposites[J].EngineeringWith Computers,2014,30(4):609-625. [5] B?HM H J,RASOOL A.Effectsofparticleshapeonthe thermoelastoplasticbehaviorofparticlereinforcedcomposites [J].InternationalJournalofSolidsandStructures,2016,87: 90-101. [6] CHAWLA N,SIDHU RS,GANESH V V.Three-dimensional visualizationandmicrostructure-basedmodelingofdeformation inparticle-reinforcedcomposites[J].Acta Materialia,2006,54 (6):1541-1548. [7] 宋卫东,王静,刘海燕.颗粒增强复合材料真实结构有限元建模 [J].北京理工大学学报,2009,29(6):501-505. SONG W D,WANGJ,LIU H Y.Finiteelementmodelofreal structureforparticlereinforcedcomposites[J].Transactionsof BeijingInstituteofTechnology,2009,29(6):501-505. [8] 邵军超,刘越.颗粒增强金属基复合材料力学行为有限元模拟 研究现状[J].材料导报,2007,21(9):111-115. SHAOJC,LIU Y.Areviewoffiniteelementsimulationson themechanicalbehaviorforparticlesreinforced metalmatrix composites[J].MaterialsReview,2007,21(9):111-115. [9] LATYPOV M I,SHIN S,DE COOMAN B C,et al. Micromechanicalfiniteelementanalysisofstrainpartitioning inmultiphasemedium manganeseTWIP+TRIPsteel[J].Acta Materialia,2016,108:219-228. [10] 王骏思.铁素体/贝氏体双相钢在循环载荷作用下变形行为的 模拟研究[D].秦皇岛:燕山大学,2019:34-45. WANGJS.Simulationstudy on deformation behaviorof ferrite/bainitedual-phase steelundercyclicloading[D]. Qinhuangdao:YanshanUniversity,2019:34-45. [11] 申刚.双相钢连续退火过程组织演变的计算模拟[D].上海: 上海交通大学,2018:35-55. SHEN G.Simulation of microstructure evolution during intercriticalannealing ofcold-rolled dual-phasesteel[D]. Shanghai:ShanghaiJiaotongUniversity,2018:35-55. [12] WANGB X,QIU F,CUI W W,etal.Microstructureand tensilepropertiesofgraphiteductileironimprovedbyminor amountofdual-phasedTiC-TiB2 nanoparticles[J].Advanced EngineeringMaterials,2021,23(8):2100246. [13] DAO M,CHOLLACOOP N,VAN VLIET K J,et al. Computationalmodelingoftheforwardandreverseproblems ininstrumentedsharpindentation[J].ActaMaterialia,2001, 49(19):3899-3918

< 文章来源>材料与测试网 > 机械工程材料 > 46卷 >