分享:基于Bayesian采样主动机器学习模型的6061铝合金成分精细优化
1.
2.
3.
结合高通量材料制备实验与基于Bayesian优化采样策略的主动学习方法,开发了有效的机器学习模型来描述合金元素组成与硬度之间的关系,并分析关键微量元素含量对硬度的影响。研究发现,经过3轮迭代64个铝合金样品建模后,Bayesian取样策略方法的预测硬度误差为4.49 HV (7.23%),远低于应用人工经验采样法的机器学习模型误差9.73 HV (15.68%),且当铝合金中的Mg和Si比值Mg/Si在1.37~1.72时,具有较高的合金硬度。通过在6061铝合金标准名义成分范围内进行成分精细优化以及性能调控,为工业上提高产品质量提供了可实现的策略.
关键词:
6061铝合金具有强度高、塑性好、可焊性及耐腐蚀性能优异的特点,在航天固定装置、轨道运输、电器装置、通讯设备和精密加工等领域有着广泛的应用[1]。6061铝合金包含Mg、Si、Mn、Fe等9种合金成分,其细微的成分变化可对其力学性能产生显著影响。在铝合金生产实践中,利用真空熔炼和电磁搅拌技术能够将元素含量控制在比国标名义成分更精细的成分范围内。通过改变合金成分,优化微观组织,可以进一步提高材料的力学性能,扩展材料的工业应用范围。有效的合金成分设计方法可以低成本加速合金的性能优化,减少耗时费力的盲目试错。多元合金的成分组合复杂,合金成分的理性设计在理论上极具挑战。在标准合金名义成分范围内进行成分精细优化,可实现性能精准调控,深入挖掘材料潜在性能,提高产品稳定性,具有重要的科学意义和应用价值。
传统的材料设计主要基于经验知识与实验试错法[2]。以6061铝合金为例,已有研究表明合金中的Mg与Si在熔炼过程中形成Mg2Si共晶组织,可以显著提高合金强度[3~5];Mn与Cr可以中和Fe的副作用[6,7];少量Cu和Zn可以提高硬度[8];Ti能控制细化晶粒,防止再结晶晶粒长大[9]。但像6061铝合金这样组成成分极其复杂,具有巨大的未知成分组合空间,基于传统认知还很难理解其精准性能调控规律,这使得新材料的研发及性能优化周期变得十分漫长[10~12]。因此除了传统的定性认识,还需要定量化或半定量化地描述模型指导实验设计[13]。
随着材料基因组计划的提出,高通量实验与计算模拟、机器学习结合的主动学习框架被广泛应用于新材料设计研发[14~16]。其中高通量材料制备和表征方法具有自动化、多工位、并发式的特点,能够实现大批量样品的快速合成和结构性能表征,从而可以低成本加速整个材料研发流程,成为快速高效获取高质量实验数据的重要手段[17]。利用统计模型[18~20]和机器学习手段[21~25],尤其是基于飞跃性发展的深度神经网络方法[26~28]的数据驱动研究能够依据已有实验数据,快速建立材料成分、结构与性能之间的定量化关系模型从而加速设计预测新材料[29]。当实验数据不充足时,经验采样、综合过采样和贪婪采样等统计经验采样方法及粒子群算法、遗传算法和Bayesian优化算法等自适应采样策略能够在未知组成空间中选取包含丰富信息量的高质量实验点填充数据集,减少实验次数,提高模型的预测能力[30~33]。近年来,机器学习模型的解释工具不断更新,使得材料性能预测模型中各输入特征的贡献程度可视化,能够定量化地解释成分、结构与材料性能之间的关系,从而加速指导目标性能材料的优化设计[34,35]。
基于此思想,本工作应用主动学习与模型解释相结合的材料优化设计框架,进一步实现了国家标准范围内6061铝合金微量元素成分的定量调控与精细优化。最终Bayesian优化采样数据填充的机器学习模型预测误差为4.49 HV (6.12%),接近测试样品实验误差4.05 HV。该成分-硬度机器学习模型能够提供优化6061铝合金成分配比。此外,结合Shapley解释法(Shapley additive explanations,简称SHAP)及部分关系依赖图 (partial dependence plot,简称PDP)分析等模型解释策略分析可得6061铝合金成分与硬度间的定量关系及组合影响[36],为企业生产工艺流程的“窄窗口”设计提供指导建议。同时,该材料优化设计框架也可为其他多元合金材料设计及性能优化提供可行的解决方案。
本工作中的主动学习与模型解释相结合的材料优化设计框架如图1所示。采用高通量实验获得硬度数据作为初始训练集,并引入具有物理意义的复合性质,对其进行重要性及相关性检验,选取可以提高模型效果的性质与成分一同作为输入特征,建立机器学习模型。每轮依据差异性准则(diversity)和不确定性准则(uncertainty),采用人工经验统计采样及Bayesian优化采样策略,选取数据点进行高通量实验,迭代更新机器学习模型,直至模型精度满足评估标准后,对最终的预测模型进行解释分析。
图1 主动学习合金设计框架
Fig.1 Active-learning framework of alloy design
本工作采用全流程高通量合金制备和表征系统,批量制备6061铝合金国标成分范围内系列铝合金样品。首先通过配粉、混合和压制过程,将高纯金属粉(99.99%)按预设的合金成分制备成圆柱块体,然后在Ar气保护气氛下使用EQ-SP-MAM-32TA高通量电弧熔炼系统制备铝合金样品。高通量电弧熔炼系统一次流程可自动炼制最多32个不同成分配比的样品。为改善样品成分均匀性,每个样品反复熔炼5次。合金样品镶嵌在树脂中后进行磨抛。最后使用MH-5L自动显微Vickers硬度计测试不同成分样品的Vickers显微硬度,检测力为0.98 N,保载时间为5 s。对每个样品不同区域测试10个点,计算平均硬度和标准均方根误差作为后续统计分析的原始数据。
为了保证初始输入训练集在全局名义成分范围内的分散性和代表性,首批合金成分设计在MgaCubMncCrdZneTifFegSihAl(1 - a - b - c - d - e - f - g - h) (质量分数,%)铝合金中各合金元素的国家标准范围(Si 0.4~0.8,Fe
如果对6061铝合金国家标准名义成分范围区间内各微量元素进行0.1% (质量分数)等间隔划分并排列组合,理论上可产生33600个符合国家标准合金组分的铝合金成分配比,这些潜在合金成分的合金硬度未知,作为本工作中搜索采样的无标签未知成分空间(unlabeled)。
根据文献调研及经验总结,单纯使用化学成分配比信息作为机器学习模型的输入特征效果是不理想的。通过在基础性质上结合成分信息构建复合性质特征,可以提高机器学习模型拟合精度。因此,本工作除使用9种化学成分特征外,以XenonPy材料信息API作为材料数据库的接口[37],通过elements_completed命令获取94个元素(从H到Pu)的58个基础性质,计算获得290个以化学成分摩尔比为权重复合性质。并与从文献中收集得到的19个基于合金专业知识构建的复合性质一同作为机器学习初始性质特征。在特征选择阶段,利用过滤法(filter)、嵌入法(embedding)和包裹法(wrapper) 3类特征选择方法对初始性质特征空间进行筛选降维,确定最终与目标性质独立相关的重要性质特征子集。
铝合金“成分-硬度”映射关系属于非线性相关的复杂问题。本研究在模型方法测试阶段选取5种经典的适用于非线性回归问题的机器学习算法进行性能评估。① 梯度提升回归(gradient boosted regression,简称gbr):应用Boosting集成算法进行非线性拟合;② 随机森林回归(random forest regression,简称rfr):基于决策树的改进Bagging回归;③ 具有多项式核函数的支持向量回归(polynomial kernel functions for support vector regression,简称svr.poly):通过添加多项式项使数据线性可分;④ 具有径向基核函数的支持向量回归(radial basis function support vector regression,简称svr.rbf):应用类Gaussian函数依靠升维实现非线性映射;⑤ 反向传播神经元网络(back propagation neural network,简称bpnn):使用误差信号回传算法的多层感知机。以上机器学习算法中均采用网格搜索及学习曲线评价的方式选取确定最优超参数。
本工作引入5种回归模型评价函数评估机器学习模型的预测准确性及泛化能力,包括用平均绝对误差 (mean absolute error,简称MAE)、均方误差(mean square error,简称MSE)和均方根误差(root mean square error,简称RMSE)作为误差统计量评估模型损失,可释方差得分(explained variance score,简称EVS)和中值绝对误差(median absolute error,简称MedAE)评估模型预测能力。EVS结合MedAE可以在解释变异与衡量模型信息捕捉能力的同时减弱实验值中存在误差异常值的影响。5个评价函数的计算分别由式(
式中,y为实验硬度;
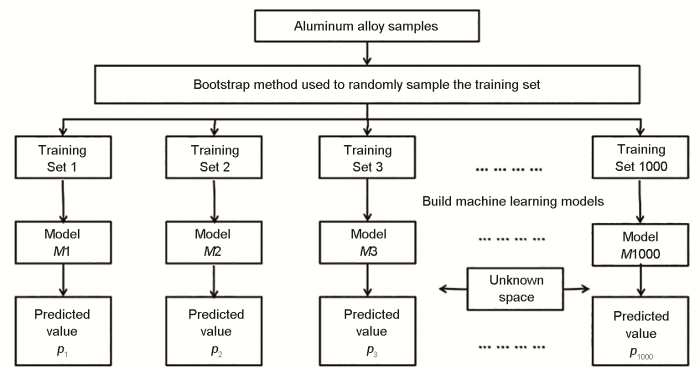
首先采用Bootstrap方法(如图2所示)对32个正交设计的初始数据进行有放回的随机抽样,产生1000个含有32个样品的训练数据集,训练获得1000个对应的机器学习模型(M1, M2,
图2 Bootstrap 随机抽样建模法
Fig.2 Bootstrap random sampling modeling method
式中,pi为1000次取样建模中,模型Mi对未知空间的预测值。
材料性能测试通常昂贵耗时,这使得高质量材料性能数据较少。针对材料科学中常见的小数据集问题,数据采样策略对提高机器学习模型预测精度至关重要。本工作采取下面2种数据采样策略选取下一步的实验合金成分,以期用较少的实验数据获得更准确的预测模型,使得成分设计迭代过程尽快收敛,达到加速材料成分设计流程的目的。
(1) 人工经验采样(manual empirical sampling,简称ME):传统机器学习指导实验中专家利用专业知识和传统经验对数据样本进行人工标记。每轮实验迭代优化根据机器学习模型预测结果及标记样本的数据结构特点,针对硬度分布不均的特点,在数据分布较少的区域内人工选取16个可能有价值的采样点。观察发现初始样本中高硬度区间(硬度> 70 HV)数据稀缺,约占所有数据的1/3。故前几轮人工经验取样偏向在高硬度预测区域,结合已有微量元素作用专业知识,选取一定量成分配比差异化的样本来填补数据集,这样可以有效避免数据重采样,使得数据点在各硬度区间的数量分布尽量均匀,提高对高硬度值预测的可信度。
(2) Bayesian优化采样(Bayesian optimization sampling,简称BO):基于Bayesian优化算法对数据样本进行自动标记。Bayesian优化算法是利用先验知识逼近未知目标函数的后验分布,自动采样策略基本思想是平衡“探索”(exploration)和“开发”(exploitation)的需求。“开发”意味着倾向于高均值,根据后验分布,在最可能出现最优解,即高硬度对应的区域进行采样。“探索”意味着倾向于高方差,模型稳定性不佳,不确定性和误差大时,通常是在取样密度小的区域获取采样点以提高模型的预测精度,减少预测值的波动。在实验迭代优化过程初期数据不完备时,首先倾向“探索”策略,重点是完善模型预测精度。随着数据逐渐增多,模型预测精度提高,逐渐转向“开发”策略,重点是寻找最优的目标值。
Bayesian优化包括2个核心过程,均需选用先验函数(prior function,简称PF)与采集函数(acquisition function,简称AC)。常见的采集函数包括上置信界(upper confidence bound,简称UCB)、改善概率(probability of improvement,简称PI)和预期改善(expected improvement,简称EI)。本工作选用EI方法作为采集函数,假定目标函数模型f(x)服从Gaussian过程,在第t轮迭代中,样本点D{(x1:t, y1:t)}对于f(x)进行估计和更新,更新后ft + 1的后验概率分布P(ft + 1?D1:t, xt + 1)~N(μ, σ2),采集函数E(I)可定义如下:
式中,ψ(z)为概率密度函数,Φ(z)为累计分布函数,σ' = σ - err。fbest为预期改善最佳采样位置,当fbest =ymax (ymax为实验硬度最大值)时,采样策略被称作高效全局优化(efficient global optimization,简称EGO);当fbest = μmax (μmax为预测硬度最大值)时,采样策略称作知识梯度(knowledge gradient,简称KG)。由于在σ'→∞时,E(I)→σ';σ'→0时E(I)→(fbest - μ),故当模型不确定度偏大时,采集函数偏向于选取减小模型不确定度的数据点,即“探索”;当模型不确定度偏小时,采集函数偏向于选取高硬度区域的数据点,即“开发”。因而Bayesian优化采样策略根据预测分布及模型不确定性,合理地平衡“探索”和“开发”2方面的需求,以少量的采样数据点提供更多样化的信息,以构建更准确的映射关系模型。
本工作中的BO采样策略具体采用EGO算法、KG算法、最大硬度布点法和最大误差布点法4种方法,每种方法各取4个数据点,每步设计一共16个实验合金成分进行下一轮实验。
建立“黑盒子”暗箱预测模型通常不能够帮助深入了解模型决策以及各合金元素作用机制。为建立6061铝合金的成分精细优化设计准则,需要发展模型解释策略。模型解释不仅可以确认模型的信任度,还可以阐明数据内在规律、指导新数据采集以及总结新的专业知识规律。本工作中应用SHAP法探究特征在给定范围内对目标变量的相对影响及重要性程度分析,并应用PDP探究特征对目标变量均值及其变化范围的绝对影响。
Shapley值常被用来解释机器学习的预测,其中“总支出”就是数据集单个实例的模型预测值,“玩家”是实例的特征值,“收益”是该实例的实际预测目标值减去所有实例的平均预测值。SHAP方法由下式定义[38]:
式中,
PDP是一个直观的模型全局解释分析图。PDP分析描述机器学习模型中1个或2个特征的边际效应,适用于探索某个特征x与目标变量y的直接关系。由PDP可以判断x与y之间的关系是线性、单调还是更复杂的非线性关系。PDP通过
PDP的计算假设所有的特征两两不相关,xs为PDP所需要绘制的特征,xc为模型中使用的其他特征。
特征工程中的特征选择对机器学习模型的预测精度具有重要影响。选取合适的特征不仅可以减少预测过拟合、提高信噪比、防止维度灾难、提高预测泛化能力,还可以使模型获得更好的可解释性。本工作首先选用过滤法(filter)按照发散性的统计检验及相关性指标来选择特征。由于低方差的特征预测效果往往不好,计算并移除309个初始性质特征中所有具有零方差的特征,剩余185个特征。将32个正交设计的铝合金样品从上到下按硬度递增顺序,排列并绘制相对于185个特征的硬度相关性热图,其中部分描述符的色阶没有特定的规律模式,与硬度测量值之间相互独立,相关性较弱,无法提供有效的信息共享。为进一步进行特征选择,使用互信息法捕获特征与硬度间的线性与非线性关系,通过
式中,p(x)为x的概率,p(y)为y的概率,p(x, y)为x、y的联合分布概率。
然后进一步根据权值系数对83个特征采用嵌入法(embedding)进行筛选,通过模型给出的特征优劣性评分,保留其中高于平均权重(1 / 83 = 0.12)的22个重要特征(表1)。
表1 22个重要性质特征描述符的索引及对应含义
Table 1
由于剩余22个重要特征之间可能存在高度线性相关:在其中1个特征提供了足够的信息之后,与之高度相关的其他特征往往无法提供额外的信息。为防止预测模型的性能受到“多重共线性”问题的影响,计算Pearson相关系数矩阵对其进行相关性筛选,结果如图3所示。相关系数在±0.9以上的特征被归成同类,共划分为5组。对每组特征进行Xgboost模型特征重要性评分获得每组中评分最高的特征(分别为F_1、F_5、F_16、F_17、F_18)。并与其他9个独立不相关特征(F_6、F_7、F_8、F_9、F_12、F_13、F_14、F_19、F_20)一起被保留(14个特征)进行下一步筛选。
图3 Pearson相关性特征筛选结果
Fig.3 Pearson correlation feature selection results (Features in black are those selected from five groups with higher feature importance. Features in red are those not selected)
由于剩余搜索空间中共存在16383种特征子集组合,为进一步缩小特征空间,综合考虑精度及效率,采用2种启发式包裹特征选择方法(wrapper)对剩余14个特征进行建模及最终比较筛选,将特征子集搜索范围降低至210种,其中100次建模模型的10折交叉验证RMSE均值作为特征子集的评价指标。
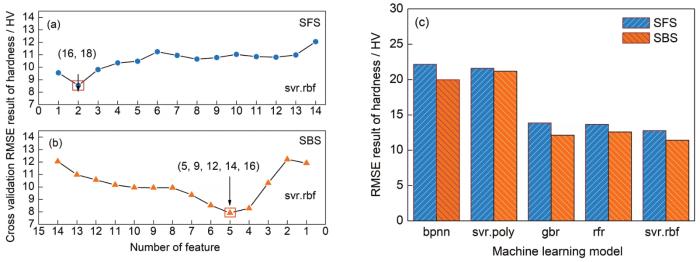
(1) 序列前向选择(sequential forward selection,简称SFS),从空集开始,每次选择一个特征x加入特征子集X1使得预测误差最小。如图4a箭头所示,特征子集X1 = (F_16, F_18)具有最小的RMSE均值。
图4 序列前向选择(SFS)与序列后向选择(SBS)特征选择方法与结果对比
(a) subset building results of SFS (RMSE—root mean square error, svr.rbf—radial basis function support vector regression)
(b) subset filtering results of SBS
(c) comparisons of modeling results between the two feature subsets (bpnn—back propagation neural network, svr.poly—polynomial kernel functions for support vector regression, gbr—gradient boosted regression, rfr—random forest regression)
Fig.4 Feature selection method and result comparisons between sequential forward selection (SFS) and sequential backward selection (SBS)
(2) 序列后向选择(sequential backward selection,简称SBS),从特征全集开始,每次剔除一个特征x构成子集X2使得模型精度最优。如图4b所示,特征子集X2 = (F_5, F_9, F_12, F_14, F_16)具有最小的RMSE均值。
为确定最终建模特征子集,按照训练集和测试集比例9∶1划分初始数据集。图4c显示X1和X2在rfr、svr.poly、svr.rbf、bpnn和gbr 5种回归模型对测试集预测的RMSE结果。在各模型上特征子集X2表现均优于X1,故首轮建模将采用SBS法筛选的性质特征子集X2与铝合金成分摩尔比组合作为机器学习模型特征空间。在后续迭代建模的过程中,针对不同的训练样本,重新根据上述特征选择方法流程,选择该轮适用的特征子集。
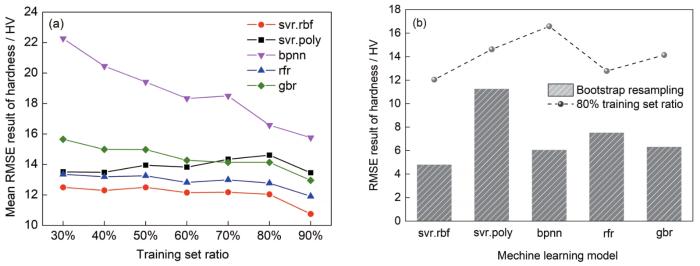
首先,在30%~90%间按照10%间隔随机划分训练数据集,使用5个回归模型对数据分别进行100次重复建模。图5a为测试集RMSE预测硬度均值结果。可见,svr.rbf 和rfr误差较低,总体表现较好。为进一步评估各模型的稳定性与泛化能力,计算5种回归模型应用Bootstrap方法随机抽样100次的全样本空间预测结果。图5b为Bootstrap采样的全样本建模预测的RMSE均值与前述训练集比例为80%时测试集预测的RMSE均值在5种算法中的预测行为对比结果。可见,2种RMSE误差均在svr.rbf模型处达到最小值。该结果的产生是由于svr.rbf适用于小样本数据集的模型特点,使其在首轮模型选择结果中展现了综合优势,最终将其选为第1轮建模实际应用算法,后续迭代建模时采取类似方式确定每轮最佳机器学习算法。
图5 机器学习模型预测结果对比
(a) RMSE results with the training data divided randomly at the ratio of 30%~90%
(b) evaluation results of Bootstrap random sampling model (histogram) and model performance with 80% training data split ratio (point and line plot)
Fig.5 Comparisons among machine learning models
鉴于建立能够精准预测成分对应硬度模型的研究目标,每轮测试集的RMSE将作为首要的预测结果评价指标,MAE和MSE作为辅助误差统计量参与评估。由于数据的非线性及部分预测样本硬度区间相对集中,EVS和MedAE也将作为重要模型行为评估指标。表2给出了首轮未采样模型及每轮以人工经验采样数据填充的机器学习模型(mME)和以Bayesian优化采样数据填充的机器学习模型(mBO)对新一轮采样点的预测评估结果。
表2 回归模型评估结果
Table 2
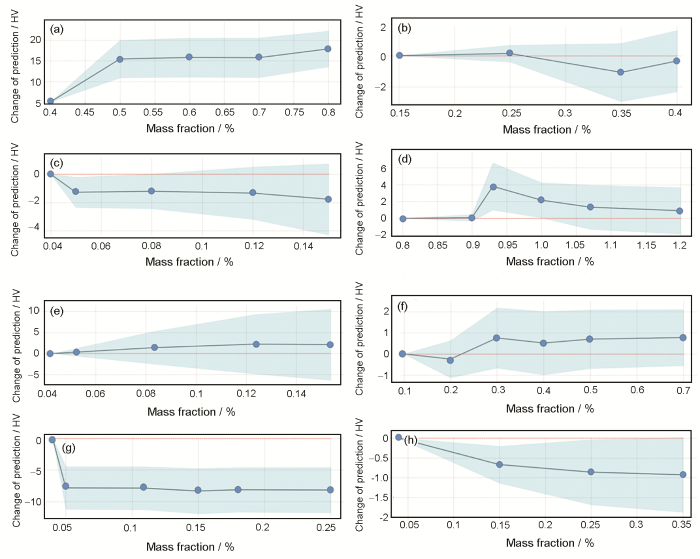
BO采样策略每轮均按照EGO、KG、最大硬度布点法和最大误差布点法4种方式,每种方式取4个点共取16个样本。首轮ME采样策略根据预测值在原始数据中样本分布较少(> 60 HV)的偏高硬度区间选取Mg和Si含量相对较高的样本点12个及随机4个实验点,但由于基础训练数据集不足,由图6a及表2预测结果所示,未进行数据补充前,使用原始数据训练的模型对于首轮Bayesian优化采样实验点(sBO)和人工经验采样实验点(sME)的预测普遍偏高,误差较大且EVS为负值,呈欠拟合状态。第2轮迭代中,为丰富数据结构并避免重采样,ME采样策略选取硬度预测值由高到低(80~50 HV)均匀分布且Mg、Cu、Si、Fe含量组合差异性较大的16个样本,由图6b及表2结果所示,预测偏高问题得到一定缓解,mME和mBO模型的MedAE均显著降低,预测效果较第1轮呈优化态势。相比之下,mBO模型EVS增至0.31且RMSE降至6.21 HV。各评估指标结果均优于同期mME模型,BO采样策略在提高模型效果上展现了初步优势。经过2轮数据填充后,第3轮建模结果如图6c及表2所示,mME预测值分散度及不稳定性在该轮得到进一步改善,EVS变为正值,但RMSE等误差统计量依然相对较高,且MedAE仍在0.03左右,模型预测存在偏差。第3轮建模结果(图6c中插图)及两模型对于未参与训练的样本的预测结果中,mBO的预测样本点大部分分散在对角线周围,与真实值基本吻合。mBO的EVS趋于0.50且MedAE降至0.007,模型的可解释性进一步增强,样本点预测大部分分散在对角线周围,与真实值基本吻合。如图6d所示,mBO模型预测硬度的RMSE由第1轮的17.31 HV降到了第3轮的4.49 HV (7.23%),比较接近该轮实验的平均误差值4.05 HV,远低于应用人工经验采样法的机器学习模型误差9.73 HV (15.68%)。用BO采样策略填充数据集并建模的优势得到进一步认可。综上可知,仅经过3轮迭代后,用64个铝合金样品建模,mBO模型对硬度预测准确度已经接近实验误差。与第3轮mME模型的预测相比,mBO模型预测结果的EVS升高212.5%,MAE降低63.03%,MSE降低78.71%,RMSE降低53.85%,MedAE降低66.67%。上述结果比较说明BO采样策略可以更有效地选取数据,对数据分布不均导致模型不确定性大的区域进行数据填充,在主动学习加速优化成分-硬度映射模型问题上占据优势,而ME采样策略初期根据还不成熟的模型预测值进行筛选,明显忽略了模型不确定性导致的误差负面影响。
图6 以人工经验采样数据填充的机器学习模型(mME)和以Bayesian优化采样数据填充的机器学习模型(mBO)建模结果对比
Fig.6 Prediction results of mME and mBO models in the first iteration (sBO—sampling based on BO, sME—sampling based on ME) (a), second iteration (b), third iteration (c), and comparisons of model error RMSE (The error bars are the mean standard deviation of the experiments) (d)
由于实验本身存在测量误差,Tian等[33]在BO采样算法的EI采集函数中引入实验误差项err,在采样阶段考虑观测噪声,有助于缩小不确定性采样空间搜索范围,减少迭代次数,加速模型优化。本工作探索建模阶段考虑观测噪声对模型预测精度的影响。首先将原始特征及硬度作为输入,实验测量误差err作为输出进行建模学习,并对33600个未知样本实验误差进行预测估计,将上述机器学习预测的实验误差作为一列独立特征量加入到原始特征空间中进行机器学习,图7及表2给出加入实验误差特征的第3轮mBO模型(记为mBOe)对未参与建模样本点的硬度预测结果。结果表明,引入实验误差并没有达到提高精度的目标,预测RMSE反而降低至6.51 HV (10.49%),且EVS变为负值。该效应的产生存在以下3种可能:误差特征引入与预测精度间可能存在负相关;机器学习预测的实验误差特征本身存在一定的不确定性;实验误差特征干扰了基础数据的规律性。基于以上分析与探索,实验误差是否适合作为建模阶段的特征量及其有效性,仍有待进一步更系统深入的考察验证。
图7 mBO与包含实验误差特征的mBO机器学习模型(mBOe)建模预测结果对比
Fig.7 Comparisons between prediction results of mBO and mBOe models
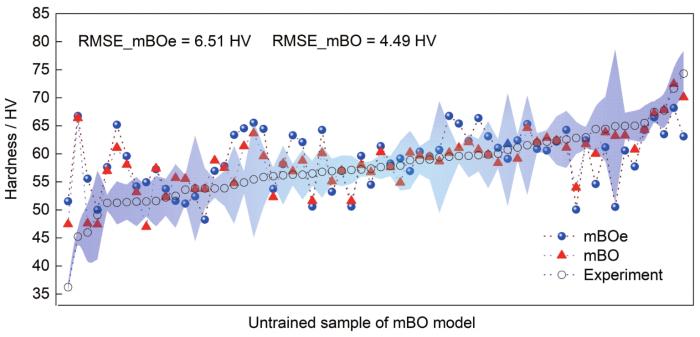
为了增强机器学习模型的可解释性和物理意义,基于SHAP与PDP等可视化模型解释工具探究分析特征对铝合金硬度的贡献程度及影响趋势。SHAP结果由图8a所示,色散变化代表特征值的高低,Y方向从上到下为特征重要性程度排序,X方向为特征SHAP值大小,SHAP值等于0对应中值样本,某点处SHAP值大于0则说明特征对于该样本点硬度预测值起到提升作用,反之减小。PDP结果如图9所示,Y值表示模型预测值相较于基线值的变化大小,折线及网格点表示特征对预测结果的影响趋势变化,阴影部分表示置信区间,置信区间越大代表该特征受其他特征变化影响较大,对硬度预测的决定性权重较小。
图8 基于Shapley解释法(SHAP)的特征重要性分析及Mg和Si相互作用关系依赖图
(a) feature importance sorting
(b) basic dependence plot of Mg
(c) basic dependence plot of Si
Fig.8 Features importance analyses and relational dependence plots of Mg and Si based on Shapley additive explanations (SHAP)
图9 微量元素特征与硬度之间的绝对变化规律及贡献性分析
(a) Si (b) Cu (c) Mn (d) Mg (e) Ti (f) Fe (g) Zn (h) Cr
Fig.9 Absolute influence of trace element features on hardness (blue shade—confidence interval, red line—baseline value)
综合上述2种机器学习模型解释策略对mBO模型预测结果进行分析发现,Si元素的影响最为显著,样本中Si含量增加对应SHAP值增大,其含量与铝合金硬度呈正相关。当Si元素质量分数在小于0.5%的区间内,其硬度估值随Si含量的增加大幅度提升,当Si质量分数在0.5%~0.7%区间内时曲线持平,其含量变化对硬度没有明显影响,直至大于0.7%后硬度再次有小幅度的提升。Cu和Mn元素重要性程度略小于Si,其含量与铝合金硬度呈负相关,当Cu的质量分数在0.25%~0.35%内时合金硬度出现明显减小,随后出现小幅度回升。而Mn的质量分数大于0.07%时硬度有降低趋势。文献[39]报道少量Mn能改善含有Cu与Si元素铝合金的高温强度,但是超过一定量后形成Al-Si-Fe-Mn四元化合物,反而起到负作用,这与本工作的机器学习预测分析一致。Mg和Ti元素质量分数与合金硬度呈正相关,且当Mg元素含量约为0.93%时积极作用最为明显,合金硬度随Ti含量缓慢增加最终至0.14%时趋于平稳。文献[39]研究表明,增加1%Mg,抗拉强度大约升高34 MPa,Ti在临界含量约为0.15%内,与Al形成TiAl2相,成为结晶时的非自发核心,起细化铸造组织和焊缝组织的作用,对提高硬度具有较好的效果。Fe、Zn和Cr元素影响远小于其他微量元素,且均呈负相关。少量的Cr元素及质量分数小于0.5%的Zn均会降低硬度预测值。已有经验表明,铝合金中若含有微量Zn,高温会使铝合金脆性增大,铸件易产生裂纹导致合金硬度及强度降低。同时需要注意铝合金热处理后合金元素的存在状态和作用也会改变。本工作针对铸态铝合金的研究主要聚焦其化学成分的本征“基因”作用和初步快速成分筛选。后续的热处理和压力加工工艺的影响和优化有待进一步研究。
图8a结果表明,最后一轮mBO机器学习模型所选择的4个性质:特征晶格畸变能、内聚能、构型熵及剪切模量,均与硬度呈正相关。材料发生晶格畸变时,原子离开平衡位置,诱发的微观应力场可阻碍位错滑移和材料变形,从而使材料强度和硬度提高。晶体的内聚能大时,金属键合较强,抵抗塑性变形能力变强,硬度会变大。构型熵增大代表微量元素含量尽可能均匀一致,也可导致硬度增加。剪切模量表示材料剪切变形的难易程度,表征材料抵抗切应变的能力,也会导致硬度变大[40]。
边际效应是在保持所有其他协变量不变的情况下,以某一解释变量变化的函数来衡量因变量的预期瞬时变化。铝合金中Mg和Si元素对铝合金性能的影响存在相关性。本工作基于SHAP计算Mg和Si元素的协同边际效应并给出相关性分析,其中垂直方向上的色散变化表示元素影响的相关性。由Mg为基础的相关性依赖图8b所示。在国标范围内,当Mg元素质量分数小于0.94%时,Si含量越低,Mg/Si越大时,SHAP贡献值越大,对应于更高的预测硬度。SHAP值大于0时,Mg/Si大于1.37。而Mg元素质量分数大于0.94%,Mg/Si比越小时。硬度预测值越高。SHAP值小于0时,Mg/Si大于1.72。类似的Si为基础的相关性依赖图如图8c所示,当Si质量分数小于0.58%时,Mg/Si越小,硬度越高,反之越低。当Mg/Si = 1.15 / 0.75 = 1.53左右时硬度预测值到达峰值,贡献效益最大化。
根据上述分析,mBO模型提供的Mg和Si协同影响结果为:当1.37 < Mg/Si < 1.72时有助于提高合金硬度及力学性能,而超出该范围时试样的力学性能骤降。当Mg/Si = 1.15/0.75 = 1.53时,合金硬度预测值达到峰值,对合金硬度及性能的贡献效益最大化。高爱华等[41]对6063铝合金的实验结果表明,合金抗拉强度、硬度和塑性都处于较优状态的Mg/Si作用范围为1.5 < Mg/Si < 1.7。而叶於龙等[5]对6101铝合金的实验结果表明,铝合金名义成分的Mg/Si = 0.53% / 0.35% = 1.514时,抗拉强度达到最佳。以上文献结果与本工作中机器学习模型分析所得结果吻合。
综上所述,基于mBO模型解释的分析可知,本工作对铝合金各微量元素及性质对硬度的影响趋势预测与实际经验吻合较好,验证了mBO机器学习模型对铝合金各微量掺杂成分与硬度等性能的关系具有良好的学习预测能力。同时获得了各元素对合金性能的影响范围及高硬度对应的最佳Mg/Si比值范围,可为6061铝合金成分定量调控及精细优化设计提供依据。
(1) 相较于根据机器学习结果及专业知识的人工经验采样策略,基于Bayesian优化算法的自适应采样策略可以更有效地指导实验。其中mBO相较同期mME的预测EVS升高212.5%、MAE降低63.03%、MSE降低78.71%,RMSE降低53.85%、MedAE降低66.67%。最终mBO模型硬度预测RMSE为4.49 HV (7.23%),与测试样品实验误差(4.05 HV)接近,初步满足成分-硬度映射模型的应用精度标准。
(2) 国家标准范围内,6061铝合金硬度随Si、Mg和Ti的含量增大而升高,随Cu、Mn、Fe、Zn和Cr含量的减小而降低,且影响程度依次下降。晶格畸变能、内聚能、构型熵和剪切模量等复合性质均与硬度呈正相关。Mg/Si对提高合金硬度及力学性能的最佳作用范围为1.37 < Mg/Si < 1.72,当Mg/Si = 1.53时达到峰值,且上述定量分析均与文献及实验结果吻合。
(3) 基于自适应Bayesian采样优化后的机器学习模型经过解释及验证,能够为在6061铝合金标准名义成分范围内进行成分优化以及性能调控提供策略指导,以提高6061铝合金产品质量的性能和稳定性。高通量实验与机器学习结合的方法可以有效加速建立一个能够对材料未知成分空间实现性能预测的机器学习模型,为后续多元合金成分精细优化设计和性能调控提供通用策略和可参考的定量化指导意见。
1 实验方法
图1

1.1 高通量实验方法
1.2 数据集构建
1.3 特征空间构建
1.4 机器学习算法及其模型评价函数
1.5 数据采样策略
图2
1.6 模型解释策略
1.6.1 SHAP
1.6.2 PDP
2 实验结果
2.1 特征选择结果
Feature index
Feature name
Feature index
Feature name
F_0
Ave: electron_affinity
F_1
Ave: hhi_r
F_2
Var: covalent_radius
F_3
Sum: atomic_weight
F_4
Var: gs_est_fcc_latcnt
F_5
Var: atomic_radius
F_6
Modulus mismatch
F_7
Var: atomic_radius_rahm
F_8
Shear modulus
F_9
Lattice distortion energy
F_10
Mixing enthalpy
F_11
Parameter omiga
F_12
Ave: dipole_polarizability
F_13
Sum: c6_gb
F_14
Cohesive energy
F_15
Var: molar_volume
F_16
Var: first_ion_en
F_17
Ave: covalent_radius_pykko_triple
F_18
Ave: boiling_point
F_19
Sum: heat_of_formation
F_20
Configurational entropy
F_21
Ave: electron_negativity
图3
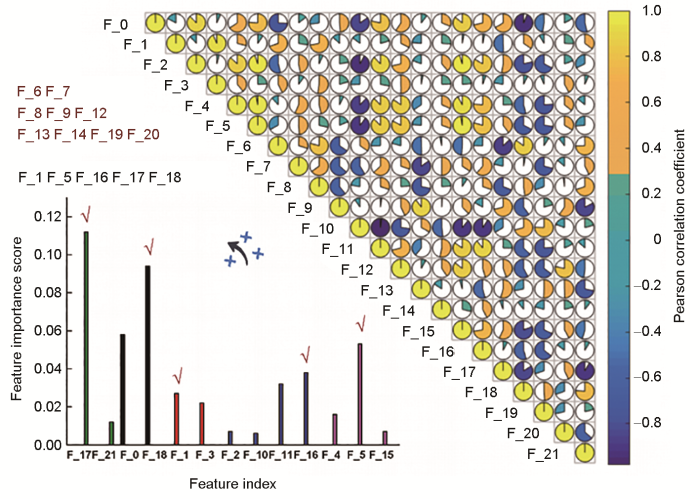
图4
2.2 回归模型选择结果
图5
2.3 采样建模结果
Round
EVS
MAE / HV
MSE / HV
RMSE / HV
MedAE / HV
First round
-0.10
14.60
301.80
17.31
0.09
The second round of mME
-0.11
10.06
138.10
11.75
0.04
The second round of mBO
0.31
5.57
38.56
6.21
0.01
The third round of mME
0.16
7.79
94.59
9.73
0.03
The third round of mBO
0.50
2.88
20.13
4.49
< 0.01
The third round of mBOe
-0.06
4.85
42.41
6.51
0.01
图6
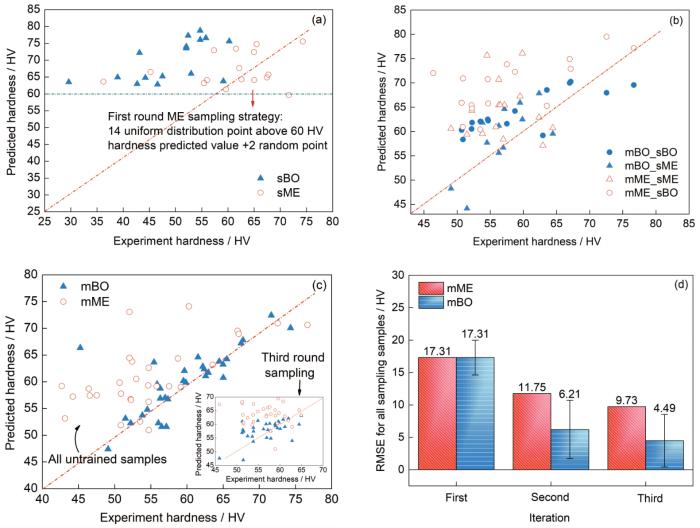
图7
3 分析讨论
图8
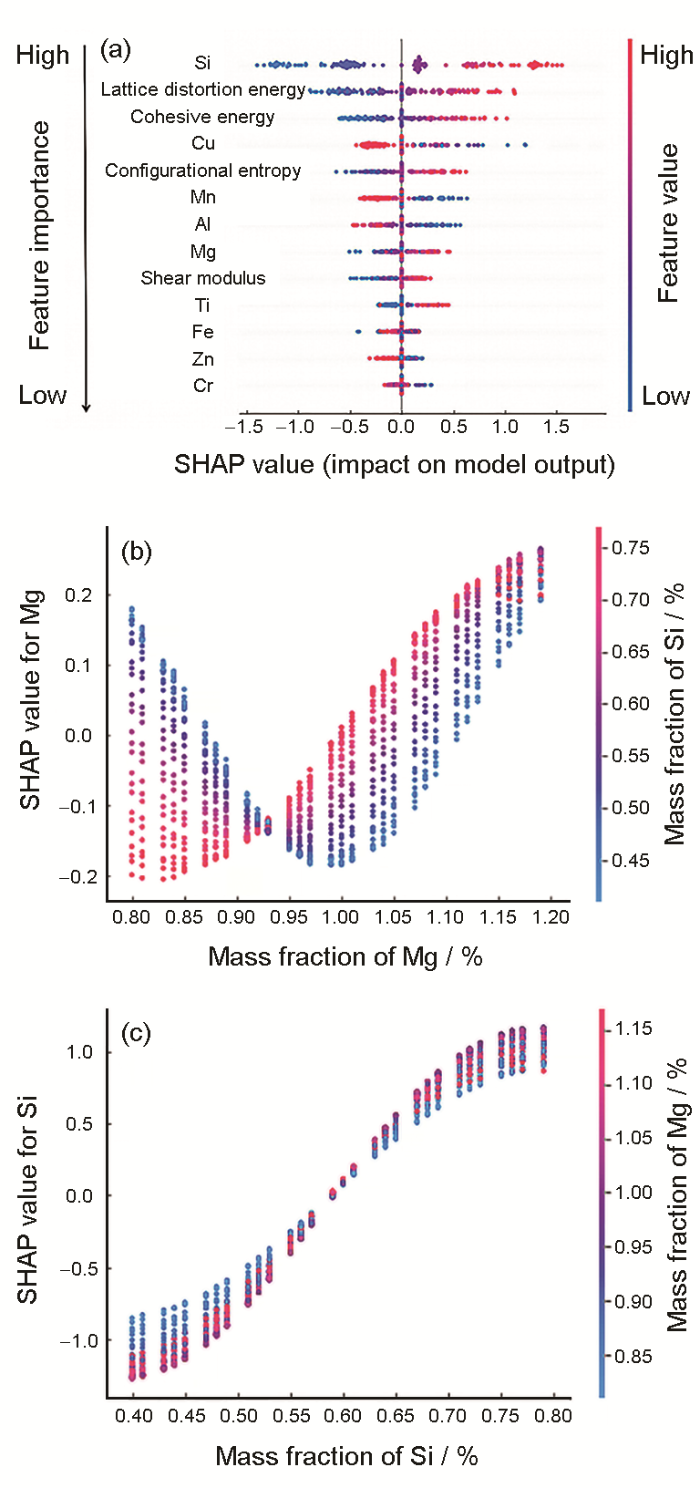
图9
4 结论
来源--金属学报







 沪公网安备31011202020290号
沪公网安备31011202020290号
