当前位置：首页 » 国检检测新闻中心 » 检测百科 » 分享：立方晶体弹性常数和EAM/FS势函数的关系

分享：立方晶体弹性常数和EAM/FS势函数的关系

来源：国检检测查看手机网址

扫一扫!

扫一扫!

浏览：- 发布日期：2024-12-31 09:26:09【大中小】

段灵杰, 刘永长,

天津大学材料科学与工程学院水利安全与仿真国家重点实验室　天津 300354

摘要

为了确定bcc和fcc晶体的EAM/FS势函数参数，研究了EAM/FS势函数与弹性常数的关系。对bcc和fcc结构晶体，分别导出压强(P)和体积弹性模量(B)、弹性常数(C44)和剪切弹性模量(Cp=(C11-C12)/2)的利用嵌入函数、对势函数和电子密度分布函数的表达式。发现C44和Cp的大小不仅取决于所考虑的原子和周围原子的距离，还受近邻原子排列状况的影响。将关于结合能(utot)和P、B、C44、Cp的5个拟合方程转化为求最小值的优化模型，给出了5种典型bcc结构晶体(V、Mo、Nb、Ta、W)和3种典型fcc结构晶体(Cu、γ-Fe、Ni)的结合能中待定参数的值。采用上述参数计算得到的最小结合能与实验结果一致，此时所对应的原子间距与晶格常数相同，表明了方法的有效性。

关键词：立方晶体 ; 弹性常数 ; EAM势 ; FS势

势函数被广泛应用于金属体系的分子动力学模拟，是计算过程中重要的基本参数之一[1,2,3,4,5,6]。为了弥补对势在过渡金属建模时的不足，人们提出了一些多体势模型。Daw和Baskes[7]基于经验和量子力学模型提出了嵌入原子方法 (embedded atom method，EAM)。同时，Finnis和Sinclair[8]根据密度泛函理论提出了Finnis-Sinclair势(FS势)。这些模型得到了广泛的应用，Zhang等[9,10]将EAM用于原子尺度的材料设计理论，并提出了修正的EAM，用以研究bcc结构过渡金属。Johnson[11,12]研究了EAM参数和空位形成能的关系，并将EAM用于合金的研究。Wang等[13,14]应用EAM计算出液态镍基718合金的密度数据，并用分子动力学模拟了单相固溶合金的热膨胀和相变。Zou等[15]用修正的EAM研究了Ti-Ni合金密度的温度依赖性。EAM模型常用于计算bcc结构过渡金属二元合金的热、动力学性质[16]，也有学者用FS势研究了Ni62Nb38合金的结构[17]和过冷Ni-Zr合金的热物理性质[18]。

EAM势和FS势基于不同的假设，但在数学上有相同的形式[19,20,21,22,23,24]。通常，EAM/FS势由2部分组成：一部分是位于晶格点阵上的原子之间的相互作用对势；另一部分是镶嵌原子在电子云中所引起的多体相互作用的嵌入势能。根据经验量子论，先对对势函数、嵌入函数和电子密度分布函数进行基本假设，而具体参数则需要实验数据拟合来确定。要通过拟合宏观弹性模量的实验结果来确定EAM/FS势函数，必须先确定弹性模量与EAM/FS势的数学关系。

对于立方晶体，有3个独立的弹性常数C11、C12和C44。广义Hooke定律可写成[25]：

\{\begin{matrix} ?_{11} = ?_{11} ?_{11} + ?_{12} ?_{22} + ?_{12} ?_{33} \\ ?_{22} = ?_{12} ?_{11} + ?_{11} ?_{22} + ?_{12} ?_{33} \\ ?_{33} = ?_{12} ?_{11} + ?_{12} ?_{22} + ?_{11} ?_{33} \\ ?_{23} = 2 ?_{44} ?_{23} \\ ?_{13} = 2 ?_{44} ?_{13} \\ ?_{12} = 2 ?_{44} ?_{12} \end{matrix}

(1)

式中，σij为应力分量，εij为应变分量(i, j=1, 2, 3)。C11和C12可以通过体积弹性模量(B)和剪切弹性模量(Cp)表示：

? = \frac{1}{3} (?_{11} + 2 ?_{12}), ?_{p} = \frac{1}{2} (?_{11} - ?_{12})

(2)

B和Cp是便于计算的[26,27]。对于C44和Cp，考虑应变能密度 $? = \frac{1}{2} \overset{}{∑_{?, ?}} ?_{? ?} ?_{? ?}$ ，由广义Hook定律，有如下表达式：

? = \frac{1}{2} ?_{11} (?_{11}^{2} + ?_{22}^{2} + ?_{33}^{2}) + ?_{12} (?_{11} ?_{22} +

?_{11} ?_{33} + ?_{22} ?_{33}) + 2 ?_{44} (?_{23}^{2} + ?_{13}^{2} + ?_{12}^{2})

(3)

应用应变张量 $? = (\begin{array}{l} 0 & ?_{12} & 0 \\ ?_{12} & 0 & 0 \\ 0 & 0 & 0 \end{array})$ ，W可简化为：W=2C44ε $_{12}^{2}$ 。因此：

?_{44} = \frac{1}{4} \frac{∂^{2} ?}{∂ ?_{12}^{2}}

(4)

应用 $? = (\begin{array}{l} ?_{11} & 0 & 0 \\ 0 & - ?_{11} & 0 \\ 0 & 0 & 0 \end{array})$ ，则W可简化为：W=(C11-C12) $?_{11}^{2}$ 。故有：

?_{p} = \frac{1}{4} \frac{∂^{2} ?}{∂ ?_{11}^{2}}

(5)

本工作先推导出弹性模量和EAM/FS势函数之间的数学关系，即确定了C44和Cp与EAM/FS势的数学表达式，随后确定了bcc和fcc结构金属中与压强(P)、B、C44和Cp有关的嵌入函数以及对势函数和电子密度分布函数的表达式，最后分析讨论了势参数的拟合中应注意的问题，并通过拟合5种典型bcc结构金属和3种典型fcc结构金属的实验数据，确定出它们的结合能参数。

已往文献[8,20,28,29]中只列出势参数的最后拟合结果，很少具体给出势函数与弹性模量之间的数学表达式，导致势函数的可靠性很难验证，也缺乏普适性。

1 弹性常数和EAM/FS势

考虑bcc或fcc结构的理想晶体，其中所有原子是等价的。因此，一个原子的结合能(utot)可写成：

\{\begin{matrix} ?_{t o t} = ?_{P} + ?_{M} \\ ?_{P} = \frac{1}{2} ∑ ? (?_{?}) \\ ?_{M} = ? (?), ? = ∑ ? (?_{?}) \end{matrix}

(6)

式中，uP是对势的贡献，uM是多体势的贡献，Σ表示对原点原子所有周围的相关原子求和，ri是所考虑的原点处的原子与周围的第i个原子间的距离，V(ri)是描述排斥的核-核作用的对势函数，?(ri)是电子密度分布函数，f(ρ)是嵌入函数，ρ表示原点原子周围的相关原子在原点处产生的电子云密度之和。

用a表示晶格常数。对于bcc结构晶体，第一层有8个原子，它们与原点处的原子有相同的距离 $?_{?} = \frac{\sqrt[]{3} ?}{2}$ (i=1, 2, $?$ , 8)；第二层有6个原子，与原点原子的距离是ri=a (i=9, 10, $?$ , 14) $。$ 同理，对于fcc结构晶体，第一层有12个原子， $?_{?} = \frac{\sqrt[]{2} ?}{2}$ (i=1, 2, $?$ , 12)；第二层有6个原子，ri=a (i=13, 14, $?$ , 18) $。$

P定义为：

? = - \frac{d ?_{t o t}}{d ?}

(7)

而B可写成：

? = - ? \frac{d ?}{d ?}

(8)

式中，Ω=a3/k是原子体积，对于bcc结构晶体，k=2；对于fcc结构晶体，k=4。

由式(6)得到W为：

? = \frac{?_{t o t}}{?} = ?_{P} + ?_{M}

(9)

这里引入了符号：

?_{P} = \frac{?}{2 ?^{3}} ∑ ? (?_{?}), ?_{M} = \frac{?}{?^{3}} ? (?)

(10)

由式(4)和(5)可导出C44和Cp的表达式。为导出C44，引入位移：

? ? = (\begin{array}{l} 0 & ?_{12} & 0 \\ ?_{12} & 0 & 0 \\ 0 & 0 & 0 \end{array}) (\begin{array}{l} ? \\ ? \\ ? \end{array})

(11)

这里x、y、z表示空间位置，ε12是小量，故有[30]：

\frac{∂ ?}{∂ ?_{12}} = ?, \frac{∂ ?}{∂ ?_{12}} = ?, \frac{∂ ?}{∂ ?_{12}} = 0

(12)

对于距离 $? = \sqrt[]{?^{2} + ?^{2} + ?^{2}}$ ，偏导数可写成：

\frac{∂ ?}{∂ ?_{12}} = \frac{∂ ?}{∂ ?} \frac{∂ ?}{∂ ?_{12}} + \frac{∂ ?}{∂ ?} \frac{∂ ?}{∂ ?_{12}} = \frac{2 ? ?}{?}

(13)

对于对势项，计算得：

\frac{∂}{∂ ?_{12}} ∑ ? (?_{?}) = ∑ ?' (?_{?}) \frac{2 ?_{?} ?_{?}}{?_{?}}

(14)

\frac{∂^{2}}{∂ ?_{12}^{2}} ∑ ? (?_{?}) = ∑ [(?_{?} ? ″ (?_{?}) - ?' (?_{?})) \frac{4 ?_{?}^{2} ?_{?}^{2}}{?_{?}^{3}} +

2 ?' (?_{?}) \frac{?_{?}^{2} + ?_{?}^{2}}{?_{?}}]

(15)

这里(xi, yi)是第i个原子的坐标。对于多体项，得到：

\frac{∂}{∂ ?_{12}} ? (?) = ?' (?) \frac{∂}{∂ ?_{12}} ∑ ? (?_{?})

(16)

\frac{∂^{2}}{∂ ?_{12}^{2}} ? (?) = ? ″ (?) {(\frac{∂}{∂ ?_{12}} ∑ ? (?_{?}))}^{2} +

?' (?) \frac{∂^{2}}{∂ ?_{12}^{2}} ∑ ? (?_{?})

(17)

用类似于式(14)和(15)的方法可得：

\frac{∂^{2}}{∂ ?_{12}^{2}} ? (?) = ? ″ (?) {(∑ ?' (?_{?}) \frac{2 ?_{?} ?_{?}}{?_{?}})}^{2} +

?' (?) ∑ [(?_{?} ? ″ (?_{?}) - ?' (?_{?})) \frac{4 ?_{?}^{2} ?_{?}^{2}}{?_{?}^{3}} +

2 ?' (?_{?}) \frac{?_{?}^{2} + ?_{?}^{2}}{?_{?}}]

(18)

利用式( $4$ )中的C44，可导出对势和多体势的贡献(C44P和C44M)分别为：

?_{44 P} = \frac{1}{4} \frac{∂^{2} ?_{P}}{∂ ?_{12}^{2}} = \frac{?}{8 ?^{3}} \sum [(?_{?} ? ″ (?_{?}) - ?' (?_{?})) \frac{4 ?_{?}^{2} ?_{?}^{2}}{?_{?}^{3}} +

2 ?' (?_{?}) \frac{?_{?}^{2} + ?_{?}^{2}}{?_{?}}]

(19)

?_{44 M} = \frac{1}{4} \frac{∂^{2} ?_{M}}{∂ ?_{12}^{2}} = \frac{?}{4 ?^{3}} [? ″ (?) {(∑ ?' (?_{?}) \frac{2 ?_{?} ?_{?}}{?_{?}})}^{2} +

?' (?) ∑ [(?_{?} ? ″ (?_{?}) - ?' (?_{?})) \frac{4 ?_{?}^{2} ?_{?}^{2}}{?_{?}^{3}} +

2 ?' (?_{?}) \frac{?_{?}^{2} + ?_{?}^{2}}{?_{?}}]]

(20)

这样C44为：

?_{44} = ?_{44 P} + ?_{44 M}

(21)

对于Cp，

? ? = (\begin{array}{l} ?_{11} & 0 & 0 \\ 0 & - ?_{11} & 0 \\ 0 & 0 & 0 \end{array}) (\begin{array}{l} ? \\ ? \\ ? \end{array})

(22)

这里ε11是小量，可得：

\frac{∂ ?}{∂ ?_{11}} = ?, \frac{∂ ?}{∂ ?_{11}} = - ?, \frac{∂ ?}{∂ ?_{11}} = 0

(23)

以及

\frac{∂ ?}{∂ ?_{11}} = \frac{?^{2} - ?^{2}}{?}

(24)

类似于C44的导出，对势和多体势对Cp的贡献(CpP和CpM)分别为：

?_{p P} = \frac{1}{4} \frac{∂^{2} ?_{P}}{∂ ?_{11}^{2}} = \frac{?}{8 ?^{3}} \sum [(?_{?} ? ″ (?_{?}) - ?' (?_{?})) ⋅

\frac{(?_{?}^{2} - ?_{?}^{2})^{2}}{?_{?}^{3}} + 2 ?' (?_{?}) \frac{?_{?}^{2} + ?_{?}^{2}}{?_{?}}]

(25)

以及

?_{p M} = \frac{1}{4} \frac{∂^{2} ?_{M}}{∂ ?_{11}^{2}} = \frac{?}{4 ?^{3}} [? ″ (?) {(∑ ?' (?_{?}) \frac{?_{?}^{2} - ?_{?}^{2}}{?_{?}})}^{2} +

?' (?) ∑ [(?_{?} ? ″ (?_{?}) - ?' (?_{?})) \frac{(?_{?}^{2} - ?_{?}^{2})^{2}}{?_{?}^{3}} +

2 ?' (?_{?}) \frac{?_{?}^{2} + ?_{?}^{2}}{?_{?}}]]

(26)

Cp为：

?_{p} = ?_{p P} + ?_{p M}

(27)

可见，Cp和C44依赖于周围原子的坐标。

2 bcc和fcc结构晶体的弹性模量

在前文讨论的基础上，分别对bcc和fcc结构晶体考虑周围的两层原子来推导弹性模量的表达式。

2.1 bcc结构晶体(k=2)

对于bcc结构晶体，第一层的8个原子有坐标： $(± \frac{?}{2}, \frac{?}{2}, \frac{?}{2})$ ， $(± \frac{?}{2}, - \frac{?}{2}, \frac{?}{2})$ ， $(± \frac{?}{2}, \frac{?}{2}, - \frac{?}{2})$ ， $(± \frac{?}{2}, - \frac{?}{2}, - \frac{?}{2})$ ，与原点原子的距离为 $?_{?} = \frac{\sqrt[]{3} ?}{2}$ ；第二层中的6个原子有坐标：(±a, 0, 0)，(0, ±a, 0)，(0, 0, ±a)，与原点原子的距离为ri=a；Ω=a3/2。在式(6)中，此时ρ= $8 ? (\frac{\sqrt[]{3} ?}{2}) + 6 ? (?)$ ，utot= $4 ? (\frac{\sqrt[]{3} ?}{2}) + 3 ? (?) + ? (?)$ 。

式(7)和(8)可写成：

? = - \frac{2}{3 ?^{2}} [2 \sqrt[]{3} ?' (\frac{\sqrt[]{3} ?}{2}) + 3 ?' (?) +

?' (?) (4 \sqrt[]{3} ?' (\frac{\sqrt[]{3} ?}{2}) + 6 ?' (?))]

(28)

? = - \frac{2}{9 ?^{2}} [4 \sqrt[]{3} ?' (\frac{\sqrt[]{3} ?}{2}) + 6 ?' (?) - 3 ? ? ″ (\frac{\sqrt[]{3} ?}{2}) -

- 3 ? ? ″ (?) + ?' (?) (8 \sqrt[]{3} ?' (\frac{\sqrt[]{3} ?}{2}) +

12 ?' (?) - 6 ? ? ″ (\frac{\sqrt[]{3} ?}{2}) - 6 ? ? ″ (?)) -

4 ? ? ″ (?) {(2 \sqrt[]{3} ?' (\frac{\sqrt[]{3} ?}{2}) + 3 ?' (?))}^{2}]

(29)

从式(19)~(21)以及(25)~(27)，计算C44和Cp，得：

?_{44} = \frac{2}{9 ?^{2}} (4 \sqrt[]{3} ?' (\frac{\sqrt[]{3} ?}{2}) + 3 ? ? ″ (\frac{\sqrt[]{3} ?}{2}) + 9 ?' (?)) +

\frac{4}{9 ?^{2}} (4 \sqrt[]{3} ?' (\frac{\sqrt[]{3} ?}{2}) + 3 ? ? ″ (\frac{\sqrt[]{3} ?}{2}) + 9 ?' (?)) ?' (?)

(30)

?_{p} = \frac{1}{3 ?^{2}} (4 \sqrt[]{3} ?' (\frac{\sqrt[]{3} ?}{2}) + 3 ?' (?) + 3 ? ? ″ (?)) +

\frac{2}{3 ?^{2}} (4 \sqrt[]{3} ?' (\frac{\sqrt[]{3} ?}{2}) + 3 ?' (?) + 3 ? ? ″ (?)) ?' (?)

(31)

2.2 fcc结构晶体(k=4)

对于fcc结构晶体，第一层中的12个原子有坐标： $(± \frac{?}{2}, \frac{?}{2}, 0)$ ， $(± \frac{?}{2}, - \frac{?}{2}, 0)$ ， $(± \frac{?}{2}, 0, \frac{?}{2})$ ， $(± \frac{?}{2}, 0,$ $- \frac{?}{2})$ ， $(0, ± \frac{?}{2}, \frac{?}{2})$ ， $(0, ± \frac{?}{2}, - \frac{?}{2})$ ，与原点的距离为 $?_{?} = \frac{\sqrt[]{2} ?}{2}$ ；第二层中的6个原子有坐标：(±a, 0, 0)，(0, ±a, 0)，(0, 0, ±a)，与原点的距离为ri=a；Ω=a3/4。在式(6)中，此时 $? = 12 ? (\frac{\sqrt[]{2} ?}{2}) + 6 ? (?)$ ，utot= $6 ? (\frac{\sqrt[]{2} ?}{2}) +$ $3 ? (?) + ? (?)$ 。

由式(7)、(8)、(21)和(27)得到：

? = - \frac{4}{?^{2}} [\sqrt[]{2} ?' (\frac{\sqrt[]{2} ?}{2}) + ?' (?) + 2 ?' (?) ⋅ (\sqrt[]{2} ?' (\frac{\sqrt[]{2} ?}{2}) + ?' (?))]

(32)

? = - \frac{4}{3 ?^{2}} [2 \sqrt[]{2} ?' (\frac{\sqrt[]{2} ?}{2}) + 2 ?' (?) - ? ? ″ (\frac{\sqrt[]{2} ?}{2}) -

? ? ″ (?) + 4 ?' (?) (\sqrt[]{2} ?' (\frac{\sqrt[]{2} ?}{2}) + ?' (?)) -

2 ? ?' (?) (? ″ (\frac{\sqrt[]{2} ?}{2}) + ? ″ (?)) - 12 ? ? ″ (?) ⋅

{(\sqrt[]{2} ?' (\frac{\sqrt[]{2} ?}{2}) + ?' (?))}^{2}]

(33)

\begin{array}{l} ?_{44} = \frac{1}{?^{2}} (3 \sqrt[]{2} ?' (\frac{\sqrt[]{2} ?}{2}) + ? ? ″ (\frac{\sqrt[]{2} ?}{2}) + 4 ?' (?)) + \\ \frac{2}{?^{2}} (3 \sqrt[]{2} ?' (\frac{\sqrt[]{2} ?}{2}) + ? ? ″ (\frac{\sqrt[]{2} ?}{2}) + 4 ?' (?)) ?' (?) \end{array}

(34)

?_{p} = \frac{1}{2 ?^{2}} (7 \sqrt[]{2} ?' (\frac{\sqrt[]{2} ?}{2}) + ? ? ″ (\frac{\sqrt[]{2} ?}{2}) + 4 ?' (?) + 4 ? ? ″ (?)) + \frac{1}{?^{2}} (7 \sqrt[]{2} ?' (\frac{\sqrt[]{2} ?}{2}) +

? ? ″ (\frac{\sqrt[]{2} ?}{2}) + 4 ?' (?) + 4 ? ? ″ (?)) ?' (?)

(35)

3 势参数的数值拟合

为完成数值拟合，首先需要确定嵌入函数、对势函数和电子密度分布函数的形式，按照紧束缚理论的经典模型，取 $? (?) = - ? \sqrt[]{?}$ ，这里A>0是待定常数。假设对势函数和电子密度分布函数为经验模型：

? (?) = \{\begin{array}{l} {(? - ?)}^{3} (?_{0} + ?_{1} ? + ?_{2} ?^{2}) & (? ≤ ?) \\ 0 & (? > ?) \end{array}

(36)

? (?) = \{\begin{array}{l} {(? - ?)}^{3} & (? ≤ ?) \\ 0 & (? > ?) \end{array}

(37)

式中，常数c和d分别表示位于第二层和第三层之间的待定的与原点原子的距离，c0、c1和c2为待定系数。对于bcc结构晶体， $? < ? < \sqrt[]{2} ?$ ， $? < ? < \sqrt[]{2} ?$ ；而对于fcc结构晶体， $? < ? < \sqrt[]{1.5} ?$ ， $? < ? < \sqrt[]{1.5} ?$ 。这样假设的对势函数和电子密度分布函数，在分界点c和d处都有连续的二阶导数。

6个待定常数A、c、d、c0、c1和c2的值，需要通过拟合utot、B、C44和Cp的实验结果以及利用平衡条件P=0来确定。对bcc结构，在A>0， $? < ? < \sqrt[]{2} ?$ ， $? < ? < \sqrt[]{2} ?$ 范围内；对fcc结构，在A>0， $? < ? < \sqrt[]{1.5} ?$ ， $? < ? < \sqrt[]{1.5} ?$ 范围内，确定6个常数，优化下式以使拟合误差最小：

? ? = (?_{t o t} - {\overset{?}{?}}_{t o t})^{2} + ?^{2} + {(? - \overset{?}{?})}^{2} +

(?_{44} - {\overset{?}{?}}_{44})^{2} + (?_{p} - {\overset{?}{?}}_{p})^{2}

(38)

式中， ${\overset{?}{?}}_{t o t} 、 \overset{?}{?} 、 {\overset{?}{?}}_{44} 和 {\overset{?}{?}}_{p}$ 分别表示utot、B、C44和Cp的实验值，ER表示拟合误差。这里仅考虑了5种典型bcc结构晶体和3种典型fcc结构晶体，利用符号计算软件MATHEMATICA解决优化问题。这些晶体的实验数据和势参数的拟合值列在表1,2,3,4中，其中在表2和4的最后一列给出了较为理想的拟合误差。表1[8]中除W之外的4种晶体，随晶格常数增大，结合能绝对值也增大。而表3[17,31]中的3种fcc晶体，随晶格常数增大，结合能绝对值减小。从表2和4的拟合误差可知，对势函数和电子密度分布函数模型(36)和(37)更适合bcc结构晶体。

表1 5种典型bcc结构晶体的实验数据(弹性常数的量纲为1011 Pa)[8]

Table 1 Experimental data for the five typical bcc structure crystals (elastic constants with dimension 1011 Pa)[8]

Crystal	a / nm	utot / eV	B	C44	Cp
V	0.30399	-5.31	1.551	0.426	0.546
Mo	0.31472	-6.82	2.626	1.089	1.516
Nb	0.33008	-7.57	1.710	0.281	0.567
Ta	0.33058	-8.10	1.961	0.824	0.524
W	0.31652	-8.90	3.104	1.606	1.590

Note: a—crystal lattice constant, utot—cohesive energy, B—bulk modulus, C44—elastic constant, Cp—shear elastic modulus

新窗口打开| 下载CSV

表2 5种典型bcc结构晶体的势参数的拟合值

Table 2 Fitted values of potential parameters for the five typical bcc structure crystals

Crystal	c	d	A	c0	c1	c2	ER
V	3.1628	3.8799	1.7110	18.83	-16.25	3.972	5.125×10-11
Mo	3.2317	4.3625	1.3678	262.85	-200.70	38.880	9.408×10-10
Nb	3.3927	4.0949	2.5909	26.30	-22.68	5.405	1.103×10-10
Ta	3.4863	4.2968	2.0498	25.13	-17.98	3.584	9.312×10-12
W	3.2601	4.4763	1.5395	275.77	-207.67	39.655	2.896×10-3

Note: A—constant in the embedding function; d—constant in the electron density distribution function; c, c0, c1 and c2—constants in the pair potential function; ER—fitting error

新窗口打开| 下载CSV

表3 3种典型fcc结构晶体的实验数据(弹性常数的量纲为1011 Pa)[17,31]

Table 3 Experimental data for the three typical fcc structure crystals (elastic constants with dimension 1011 Pa)[17,31]

Crystal	a / nm	utot / eV	B	C44	Cp
Cu	0.3615	-3.54	1.420	0.818	0.257
γ-Fe	0.3591	-4.29	1.670	1.170	0.475
Ni	0.3518	-4.45	1.876	1.317	0.552

新窗口打开| 下载CSV

表4 3种典型fcc结构晶体的势参数的拟合值

Table 4 Fitted values of potential parameters for the three typical fcc structure crystals

Crystal	c	d	A	c0	c1	c2	ER
Cu	4.0205	4.0186	0.75371	2.1130	-1.4471	0.25140	0.001806
γ-Fe	3.9921	3.9972	0.71778	3.1839	-2.3086	0.41589	0.002837
Ni	3.9107	3.9166	0.76407	3.6419	-2.7079	0.50041	0.013935

新窗口打开| 下载CSV

将参数的拟合值以及嵌入函数、对势函数和电子密度分布函数代入2.1和2.2节中的utot的表达式，将a记作R。得到utot关于R的解析表达式。图1和2分别给出了5种典型bcc结构晶体和3种典型fcc结构晶体的utot-R曲线。这些曲线中utot的最小值与utot的实验值是一致的，这个最小值所对应的R值与晶格常数一致。

图1

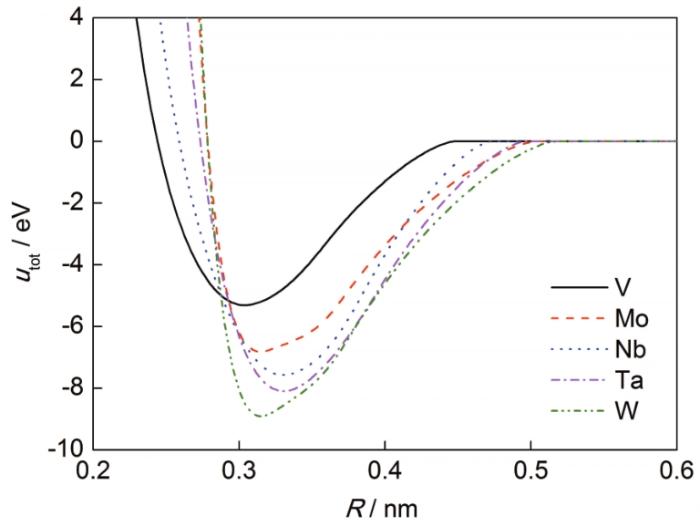
图1 5种典型bcc结构晶体的结合能随原子间距(utot-R)的变化曲线

Fig.1 utot-R curves for five typical bcc structure crystals (R—measurement of atomic spacing)

图2

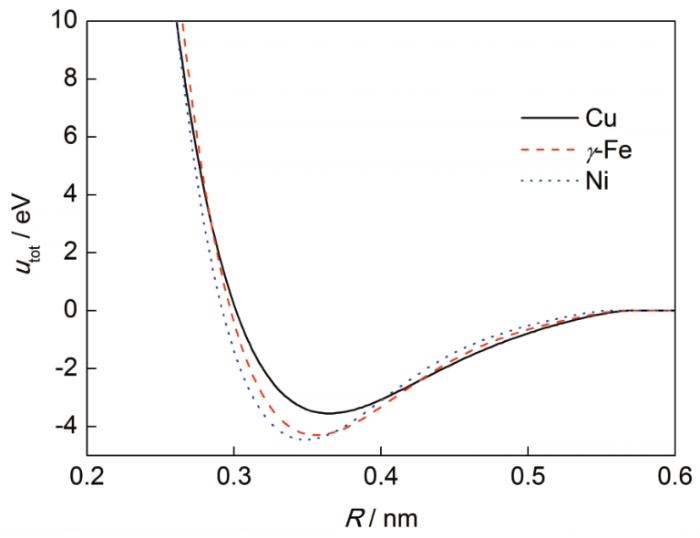
图2 3种典型fcc结构晶体的结合能随原子间距(utot-R)的变化曲线

Fig.2 utot-R curves for three typical fcc structure crystals

需要说明的是，本工作的主要研究内容仅涉及弹性模量用势函数的导出问题，由于对势函数和电子密度分布函数采用了分段函数形式，忽略了截断距离外的势能，从而不可避免地会引起R偏离a时，utot的数值误差加大。

4 结论

(1) 给出bcc和fcc结构晶体适用的EAM/FS势函数和弹性常数之间的数学关系，其中C44和Cp=(C11-C12)/2不仅依赖于所考虑的原点原子和周围原子的距离，还取决于近邻原子的排列状况。

(2) 对bcc和fcc结构晶体，利用嵌入函数、对势函数和电子密度分布函数导出了P、B、C44和Cp的表达式。推导过程中，未定义嵌入函数、对势函数和电子密度分布函数的具体函数形式，具有普适性。

(3) 使用本工作提出的方法，验证了5种典型bcc结构晶体(V、Mo、Nb、Ta、W)和3种典型fcc结构晶体(Cu、γ-Fe、Ni)的结合能。在假设含待定常数的嵌入函数、对势函数和电子密度分布函数具体表达式的基础上，将关于utot、P、B、C44和Cp的5个拟合方程转化为求最小值的优化问题，从而准确地确定了结合能中的待定参数。

来源--金属学报

下一篇：已经是最后一篇了上一篇：分享：外延膜的高分辨X射线衍射分析

“推荐阅读”

国检检测新闻中心 News Center

分享：立方晶体弹性常数和EAM/FS势函数的关系

1 弹性常数和EAM/FS势

2 bcc和fcc结构晶体的弹性模量

2.1 bcc结构晶体(k=2)

2.2 fcc结构晶体(k=4)

3 势参数的数值拟合

图1

图2

4 结论

“推荐阅读”

国检动态

检测百科

行业资讯

社会关注

公告声明

最新资讯文章