分享:含水条件下单晶Cu的应力松弛及弹性恢复
采用分子动力学方法研究了不同含水条件下单晶Cu纳米压入过程中的应力松弛和弹性恢复行为。结果表明,恒定变形量下单晶Cu承受的应力减小,发生应力松弛现象,水膜存在时单晶Cu的应力松弛量大于无水情况。纳米压入过程中Cu原子间距随压入深度增加而快速减小,应力松弛阶段Cu原子间的最邻近距离未有明显变化,卸载初期Cu原子间距因变形区域弹性能及位错能的释放而迅速增大。含水条件下单晶Cu内部形成的位错明显多于无水情况,说明不可恢复性变形量因水膜的出现而加剧;卸载结束时部分变形得以释放,促进了部分位错消失,水膜的存在阻碍了弹性恢复和塑性变形的释放。
关键词:
在维持恒定变形的材料中,应力会随时间的增加而减小,这种现象为应力松弛[1]。材料承受载荷过程中,在应力极大值处发生局部塑性变形,使材料内部的应力分布发生变化,则原先弹性分布的应力极值得以下降便体现出松弛效应,进而促使应力分布的不均匀性得以改善[1,2,3]。材料的弹性恢复反映了弹性变形原子在外力作用消失或去除后恢复到其初始位置的能力,它与材料自身属性(如弹性模量)相关。弹性变形不仅受外力影响,而且与晶体内部畸变有关,如空位、位错等缺陷周围原子排列不规则而存在弹性变形[4,5]。对于金属晶体材料而言,应力松弛和弹性恢复对材料力学、机械、电学等性能具有非常重要的影响,甚至在一定条件下会造成极大的危害。
应力松弛在狭义上不同于蠕变行为,但是可以理解为一种广义的蠕变。蠕变过程中材料在某瞬时的应力状态,一般不仅与该瞬时的变形有关,而且与该瞬时以前的变形过程有关[6,7]。同样地,应力松弛也与材料变形前后瞬时状态密切相关。在纳米尺度下,金属晶体的应力松弛现象是固体材料热散发过程的宏观表现。Torres和Voorwald[8]在研究AISI 4340钢的实验中指出,应力松弛与施加的应力大小密切相关。值得注意的是,应力松弛过程中材料的形状不会发生变化,并且直到加载去除应力松弛都是不可见的[9],这为应力松弛的理解带来困难。然而,分子动力学模拟方法的发展为材料性能的研究提供了新的视角[10,11,12]。1997年,Dong等[13]采用二维分子动力学模拟研究了错配纳米膜的低温生长和应力松弛行为。Lau等[14]采用新的方法研究了纳米晶体在宏观时间尺度上的应力应变行为,结果表明,金属材料受到外力作用而产生内应力的同时,伴随着材料内部或者微小片层滑移,材料结构发生转变。Brostow和Kubát[15]采用分子动力学模拟方法研究了理想晶体的应力松弛行为,结果表明,应力松弛主要由缺陷附近发生的变形引起,因此应力松弛过程与缺陷浓度和自由体积有关。李启楷等[16]模拟了Ni压头在Al基体上的纳米压入全过程,指出纳米压入伴随着应力弛豫过程,该过程中位错组态不断发生变化。
当材料的变形量小于其临界应变量或者所受应力小于屈服强度时,材料仅发生弹性变形,外力卸载后变形能够完全恢复。微纳尺度下,分子动力学模拟正在逐渐填补材料塑性变形过程中的弹性恢复机制研究的空缺。朱瑛等[17]在基于分子动力学的金属Ti纳米切削过程研究中表明,已加工表面原子的弹性恢复能够减缓加工过程总势能和温度不断增加的趋势。Wang等[18]对NiAl合金纳米压痕过程中的弹塑性行为进行了研究,给出了纳米单晶的弹性恢复系数的2种计算方法,并发现在NiAl合金发生塑性变形后,其弹性恢复系数随着Ni的含量变化而发生变化。Fang等[19]通过单晶Cu的纳米压痕模拟研究发现,压头卸载后,由于压头对单晶Cu的作用力减小,单晶Cu内部缺陷向基体表面运动并逐渐减少甚至完全消失,导致单晶Cu的弹性恢复发生变化。
材料的应力松弛和弹性恢复不仅取决于材料的显微结构,而且受到应力、温度、环境介质等因素的影响,其中材料所处环境或者工况条件下的润湿性或含水条件是影响材料性能的重要因素[20,21,22,23,24,25]。宏观尺度下润湿性或含水条件对材料力学性能的影响通常被忽略,然而,纳米尺度下水条件的影响随着尺度效应增强而急剧增大。含水条件下金属晶体材料的弹塑性变形是非常复杂的过程,应力松弛和弹性恢复行为的研究非常有限,特别是纳米或原子尺度下的塑性变形过程所伴随的应力松弛和弹性恢复规律及机理尚不清晰,因此有必要从原子角度对此现象深入研究,以进一步加深此方面的理解,并弥补实验研究的不足。
本工作采用分子动力学模拟方法,针对含水条件下单晶Cu的纳米压痕过程,通过设定压入变形量考察了单晶Cu基体的应力松弛现象,分析了原子间最邻近距离的变化和压头卸载过程中单晶Cu表面原子的弹性恢复行为,揭示了水膜(厚度)对应力松弛和弹性恢复的影响。从原子尺度上为纳米单晶金属材料的弹塑性变形机制的研究提供理论依据。
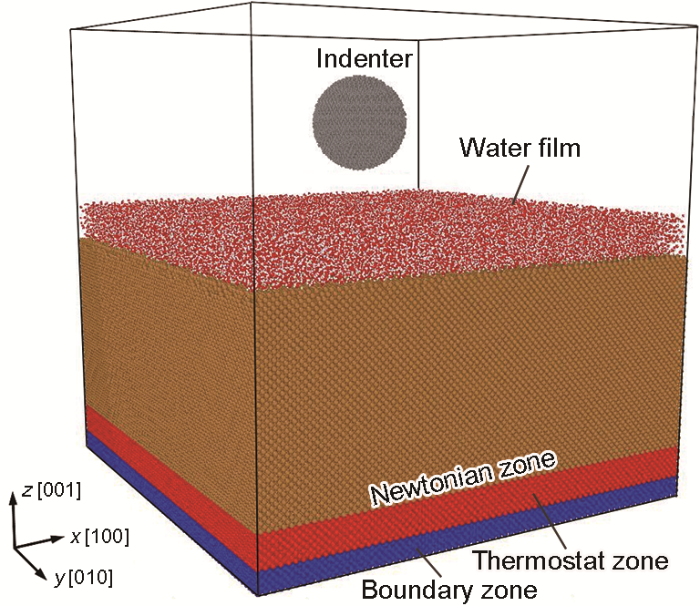
采用开源的LAMMPS软件模拟含水条件下单晶Cu的应力松弛及弹性恢复行为。初始模型如图1所示,该模型包括球形金刚石纳米压头、水膜和无缺陷的单晶Cu基体。基于金刚石结构的纳米压头半径为2.53 nm,由11954个C原子组成。单晶Cu基体沿着x [100]、y [010]和z [001] 3个晶向的尺寸分别为68a、68a和35a (其中,a=0.3615 nm,为单晶Cu的晶格常数)。单晶Cu基体由边界(boundary)层、热浴(thermostat)层和Newtonian层组成,模拟过程中边界层固定不动用以降低边界效应,热浴层用来控制体系温度,热浴层和Newtonian层的Cu原子服从经典的Newton运动规律。为研究水膜厚度对应力松弛及弹性恢复的影响,建立了3个不同厚度的水膜,其z方向的尺寸(H)分别为1.0、2.0和3.0 nm,x和y方向的尺寸与单晶Cu基体基本一致,水膜的初始密度为1.0 g/cm3。
图1 含水条件下的单晶Cu纳米压入初始模型
Fig.1 The initial model of nanoindentation of monocrystalline copper under water environment
Color online
势函数控制着原子间的相互作用形式,对模拟结果起重要作用,从根本上决定着材料的所有性能。本工作中Cu原子之间的相互作用采用金属体系最常用的势函数——嵌入原子(EAM)势,EAM势能很好地描述金属结合能的形成[26,27]。Cu原子与C原子之间的相互作用采用Morse势函数[28]:
式中,E为相互作用能,势函数极小值与解离能差D0=0.1 eV,常数α=17 nm-1,原子间平衡距离r0=0.22 nm,截断半径r=0.4 nm。本模拟中金刚石压头设为刚体,因此省略了C原子之间的相互作用。水分子之间的相互作用采用TIP4P模型[29],由于H原子对于体系的热力学性能的影响非常微小,因此H原子之间以及H原子与Cu原子、C原子之间的相互作用亦被忽略,Cu—O和C—O之间采用Lennard-Jones势函数,相关参数由Lorentz-Berthelot混合规则[24,29]计算得到,见表1[30,31,32]。
表1 TIP4P和Lennard-Jones势函数参数[30,31,32]
Table 1
Atom pair
ε
kJ·mol-1
δ
nm
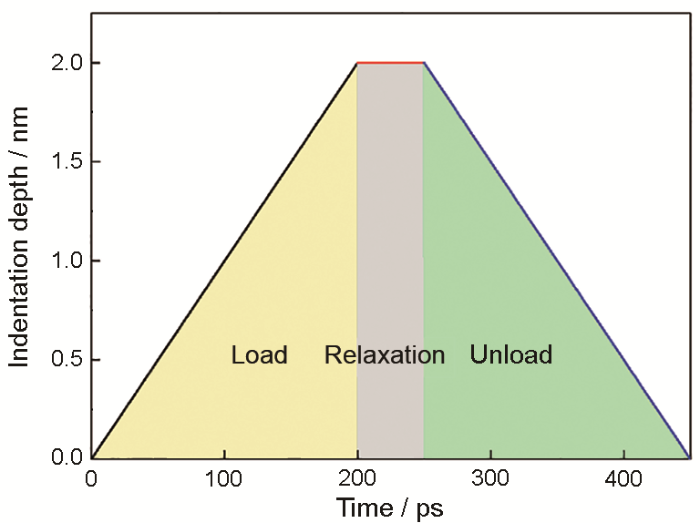
本模拟中速度积分采用Velocity-Verlet算法,模拟时间步长为1.0 fs。模型沿x和y方向设置为周期性边界条件,单晶Cu热浴层的温度采用Langevin热浴方法控制在300 K。动力学模拟之前,研究体系在正则(NVT)系综下进行50 ps的弛豫过程,使体系达到平衡。随后进行非平衡动力学模拟,包括纳米压入(load)、应力松弛(relaxation)和卸载(unload)过程,压入和卸载过程采用恒位移控制方法实现,压头运动速率和时间分别为0.01 nm/ps和200 ps (即压入深度为2.0 nm),应力松弛过程中保持压头压入结束时所处的位置不变并维持50 ps,如图2所示。模拟结果的可视化采用Ovito软件实现。
图2 纳米压痕位移控制示意图
Fig.2 Schematic of displacement-controlled nano-indentation
作者[24]在前期的工作中已经对不同润湿条件下单晶Cu的纳米压入行为进行了深入研究,结果表明,水膜的存在促进了单晶Cu初始位错的长大与扩展,而无水压入过程中大量的初始位错扩展受限,压入过程中压头与单晶Cu基体之间的水分子具有明显的力传递作用。
图3是不同含水条件下的单晶Cu的载荷-压深曲线。由该图可知,不同的水膜厚度(H)时单晶Cu基体在应力松弛过程中的载荷变化和卸载曲线存在明显的差异。卸载过程中,载荷的负值意味着压头离开单晶Cu基体时与单晶Cu原子之间存在强烈的引力作用。无水膜时引力作用最强,最大值接近90 nN,水膜存在时引力减小,这意味着水膜的存在阻碍了卸载过程中压头与单晶Cu的直接作用,与纳米压入过程类似[24,29]。
图3 无水膜及水膜厚度为1.0、2.0、3.0 nm时单晶Cu的载荷-压深曲线
Fig.3 Load-indentation depth curves of without (a), and with H=1.0 nm (b), 2.0 nm (c) and 3.0 nm (d) water films (H—water film thickness)
由图3载荷-压深曲线中应力松弛过程中载荷的变化可知,应力松弛阶段作用于压头上的载荷明显减小,即单晶Cu发生应力松弛现象,载荷的变化值随润湿条件不同而存在差异。计算发现,无水膜时单晶Cu的应力松弛量明显小于含水的情况;水膜出现时单晶Cu的应力松弛量快速增大,水膜厚度为1.0和2.0 nm时,应力松弛增长率依次达到44.0%和8.2%,而当水膜厚度为3.0 nm时应力松弛降低。显然,水膜对应力松弛的影响并非单一变化趋势。
为深入探讨水膜厚度对加载、应力松弛和卸载过程中单晶Cu的弹塑性变形的影响,计算了压头作用的截断半径内的Cu原子之间的最小距离,如图4所示,其中单晶Cu无变形时原子之间的平均距离约为2.44 nm。无水条件下,随着压头压入单晶Cu基体,接触范围内的Cu原子受压头挤压相互靠近,因此Cu原子间的距离快速减小(前50 ps),该过程中单晶Cu开始发生塑性变形并且有大量位错开始成核;随着压头不断深入基体,尽管接触范围内的Cu原子间的平均距离不断减小,但是压头周围Cu原子间的最小距离不再减小(50~200 ps),这是因为该过程中位错开始大量扩展但是并未发生位错或缺陷形式的转变,同时单晶Cu基体受到的载荷也未有明显的增大,因此原子间最小距离继续减小变得非常困难。但是,该过程中变形原子的数量随压头的持续压入而不断增多,所以塑性变形区域Cu原子间的平均距离持续减小。应力松弛阶段(200~250 ps),初期Cu原子间的最小距离略微增大,这源于位错扩展时释放的部分能量作用于被压缩原子的结果,随后最小距离未有明显的变化。卸载过程中(250~450 ps),初期由于载荷的快速释放,变形区域的弹性能快速释放,Cu原子间距迅速增大;随着卸载过程中压头不断远离单晶Cu基体和表面,Cu原子间的距离不再有明显的变化。值得注意的是,卸载过程中Cu原子间距增大主要由2个方面原因引起:(1) 压头对单晶Cu的下压力降低,促使塑性变形原子的位错能得以释放,为原子间距增大提供了动力;(2) 压头对单晶Cu的挤压力减小导致前期发生弹性变形的原子间的弹性能得以释放,原子发生弹性恢复,引起原子间距增大。
图4 不同水环境下单晶Cu的纳米压入区域最邻近Cu原子间距变化
Fig.4 The nearest interatomic separation among Cu atoms in indenting region under different water environments
有水膜存在时,单晶Cu原子最邻近距离随时间的变化与无水膜时的变化趋势基本相似。事实上,当压头与水膜初始接触时,压头下方的水膜被挤压变形并向压头四周溢出。随着压头持续下降,压头正下方的水膜在变薄的同时将压头的部分下压力传递至单晶Cu表面[24,25],导致Cu原子间距提前减小,并且相同压深下的Cu原子间距小于无水情况。当外加载荷增大到某一值时,压坑内的水分子会呈现“刚性”特征,即水分子强的H—O键和分子之间的强斥力作用使其无法继续靠近。因此,压入后期,压坑内的水分子会被压入Cu原子之间,部分Cu原子在刚性水分子的挤压下被分散开[24,25],进而引起Cu原子最邻近间距略微增大。整个压入过程中水膜厚度对单晶Cu原子最邻近间距的影响并无明显规律。应力松弛阶段,水膜厚度为1.0 nm时最邻近Cu原子间距处于压入后期原子间距波动的范围内,并且小于无水情况;水膜厚度为2.0 和3.0 nm时,最邻近Cu原子间距增大,与无水情况几乎一致。这说明较厚的水膜促进了单晶Cu的应力松弛行为。卸载阶段,压坑内水分子之间存储的弹性能非常有限,不会对单晶Cu的弹性恢复产生明显的贡献;相反,这些水分子还会吸收变形Cu原子的弹性恢复能,阻碍其弹性恢复。由图4也会发现,水膜厚度为1.0 和2.0 nm时,最邻近Cu原子间距呈现相似的趋势,并且最终稳定阶段的原子间距基本一致;水膜厚度为3.0 nm时,最邻近Cu原子间距小于前二者,说明较厚的水膜对变形原子的弹性恢复和塑性变形能量释放具有更明显的阻碍作用。
图5展示了不同润湿条件下压头卸载前后单晶Cu压坑的切片构型。可以看出,压头卸载后压坑的深度和宽度均发生了不同程度的减小,其中无水膜时的变化最明显。另外,由构型图也可以看出,压坑内Cu原子之间存在一些空洞,这些空洞是纳米压入过程中被压入的水分子占据的空间[25],这也是压入后期Cu原子最邻近间距增大的原因。
图5 无水膜及水膜厚度为1.0、2.0、3.0 nm时压头卸载前(橙色)后(蓝色)单晶Cu切片构型图
Fig.5 The slice configurations of monocrystalline copper before (orange) and after (blue) unloading of without (a), and with H=1.0 nm (b), 2.0 nm (c) and 3.0 nm (d) water films
Color online
图6展示了不同润湿条件下纳米压入过程刚结束(左)、应力松弛后(中)和卸载结束(右)时单晶Cu基体内部的位错构型和压入区域的弹性变化。可以看出,含水条件下加载结束时压入区域下方形成的位错、层错等缺陷数量明显多于无水的情况,这与作者前期研究结果[24]一致。压入结束到卸载开始前为应力松弛阶段,通过比较可以发现,压入引起的内部缺陷在应力松弛后略有减少,如部分层错原子(绿色)消失后留下局部的空位。卸载结束时,随着压头对基体的压力的去除,基体变形引起的部分能量得以释放,促进了部分位错、层错等缺陷的消失或向其它缺陷转变,因此图6中无水及水膜厚度为1.0和2.0 nm时几乎无法观察到位错和层错,水膜厚度为3.0 nm时有少许残留。另外,图中箭头显示了压痕高度的变化,卸载结束时的压痕深度和体积明显减小,说明压头卸载后压痕区域内或周围的原子发生了强烈的弹性恢复行为。
图6 无水膜及水膜厚度为1.0、2.0、3.0 nm时纳米压入过程结束(左)、应力松弛后(中)及卸载结束后(右)压痕区域的缺陷构型
Fig.6 Default configurations within monocrystalline copper after loading (left), after stress relaxation (middle), and after unloading (right) of without (a), and with H=1.0 nm (b), 2.0 nm (c) and 3.0 nm (d) water films (blue—undeformed atom, red—surface and partial dislocation atom, green—stacking fault atom)
Color online
通过计算压头从卸载开始到结束的过程中单晶Cu的最大弹性恢复量可以发现,相比于无水膜的弹性恢复,当水膜厚度增加到1.0和2.0 nm时,单晶Cu的弹性恢复量明显减小,减小幅度分别达到了18%和51%。当水膜厚度增大到3.0 nm时,弹性恢复量略有增加,但仍然明显小于无水膜的情况。显然,单晶Cu的弹性恢复量随水膜的变化规律与压头卸载过程中最邻近原子间距的变化趋势(图4)有差别。但整体而言,水膜存在时引起的原子间最邻近间距以及卸载后的弹性恢复量均减小,这说明,纳米压入过程以及应力松弛阶段引起的压痕内的不可恢复性变形因为水膜的存在而增大,卸载过程中单晶Cu基体的弹性恢复受到水膜的阻碍。这是因为在纳米压入阶段水膜存在于压头与单晶Cu表面之间,压痕较深时水分子(具有极强的O—H键)被压入Cu原子之间(形成如图5中Cu原子间的空洞)[24,25],进而对邻近的Cu原子形成更大的挤压,增大了单晶Cu的塑性变形;在应力松弛阶段,压入阶段产生的部分应力集中得到短暂的释放,因此缺陷略有减少;而在卸载阶段,当单晶Cu基体内部积聚的大量的应力或能量(包括位错能、弹性能等)得以释放时,存在于压头和单晶Cu之间的水分子又为弹性恢复和应力松弛提供了阻力。
(1) 压头悬停阶段作用于压头上的载荷明显减小,即发生应力松弛现象。无水膜时单晶Cu的应力松弛量明显小于含水情况,水膜厚度为1.0和2.0 nm时,应力松弛增长率达到44.0%和8.2%。
(2) 纳米压入过程中,Cu原子间距随压入深度增加而快速减小;应力松弛阶段,Cu原子间的最邻近距离先增大后保持不变;卸载过程中,初期Cu原子间距因变形区域弹性能及位错能的释放而迅速增大,后期基本恒定。
(3) 含水条件下加载结束时,单晶Cu内部的位错、层错等缺陷数量明显多于无水情况,说明压痕内的不可恢复性变形因为水膜的存在而加剧;卸载结束时单晶Cu的变形能量得到释放,促进了部分位错、层错等缺陷的消失或向其它缺陷的转变,但是水膜对弹性恢复和塑性变形能量的释放行为具有一定的阻碍作用。
1 模拟方法
图1
Cutoff distance
nm
O—O
0.6505[32]
0.31655[30]
0.6
Cu—O
1.1335[30,31]
0.28877[30,31]
0.5
C—O
0.4186[32]
0.32750[32]
0.5
图2
2 结果与讨论
图3
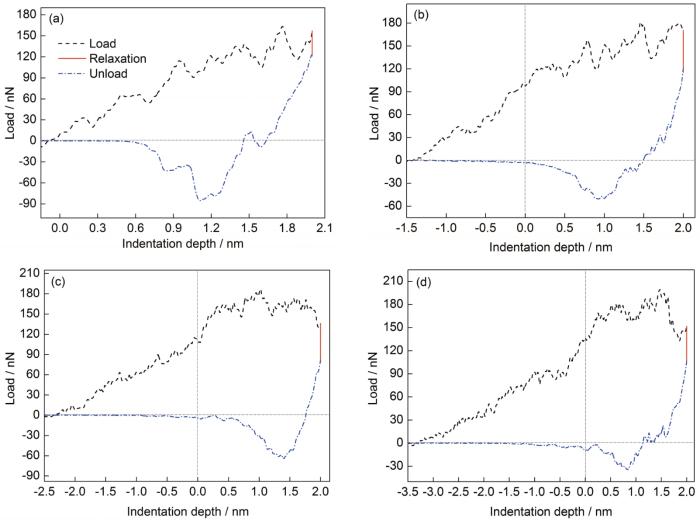
图4
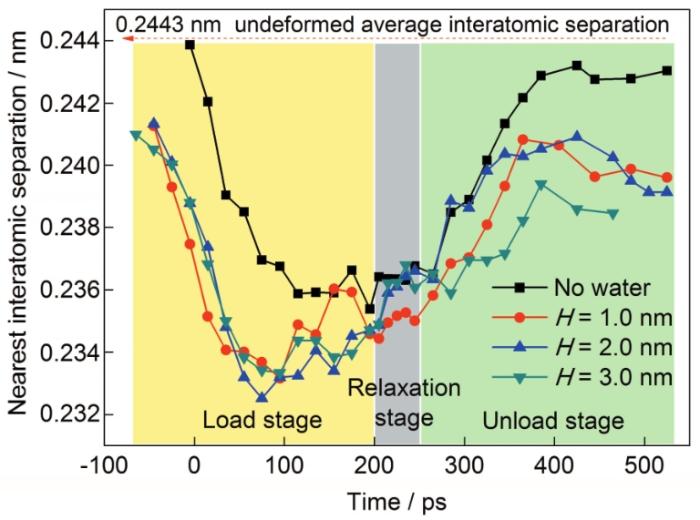
图5

图6

3 结论
来源--金属学报







 沪公网安备31011202020290号
沪公网安备31011202020290号
