周丽1, 张鹏飞1, 王全兆,2, 肖伯律2, 马宗义2, 于涛1

B4C/Al复合材料除具有高比强度、高比刚度、良好的耐磨性能及低的热膨胀系数等金属基复合材料的优点外[1,2]，由于B4C具有良好的中子吸收能力, 是近几年来备受关注的一种中子吸收材料，已经被成功运用在乏燃料水池和燃料运输容器中[3,4]。

B4C/Al复合材料的制备方法主要有挤压铸造、搅拌铸造、熔体浸渗和粉末冶金等[5,6,7]。为了提高复合材料的致密度、改善微观组织均匀性、增加材料的力学性能并形成最终产品，需要对复合材料进行塑性变形加工，如轧制、锻压或挤压等。由于大量硬脆陶瓷颗粒的加入严重阻碍了基体的塑性流动，而且提高了变形抗力，使B4C/Al复合材料的变形加工非常困难。若加工工艺参数控制不当，挤压和轧制条件下很容易导致型材的边缘开裂或内部损伤[8]。

对一种材料可加工性的完整描述，需要了解变形过程中加工参数(如温度、应变速率和应变)对流动应力的影响、材料的失效行为以及组织演化机制的转变。已有文献[9,10,11,12,13]研究了B4C/Al复合材料热变形中的流变行为及相应的微观结构变化，分析了温度和应变速率对流变应力的影响[9]。通过对高应变率下的流变应力修正，修正后的Arrhenius双曲正弦本构模型可以很好地预测B4C/6061Al复合材料的热变形行为[11]。贺玮等[12]采用不同的二次加工方法获得了抗拉强度高、组织分布均匀的B4C/Al复合材料。李德富等[13]研究了B4C/2009Al 复合材料热加工变形中发生动态再结晶的临界条件。但关于B4C/Al复合材料热变形中材料的断裂行为还少有研究。Li等[14]和Opelt等[15]分别对陶瓷和聚合物基复合材料热压缩条件下的断裂机理进行了研究。不同复合材料具有不同的细观结构，但研究结果表明，在热压缩条件下，变形温度对基体内的微孔洞、微裂纹和界面的演化等有显著影响，而且宏观上表现出的断裂形貌是由其细观组织决定的。

B4C/6061Al复合材料热变形应力、应变及损伤存在多尺度和多相性的特点，宏观尺度上(毫米级别以上)可视为均匀连续介质；细观尺度上(微米级别)则区分为性能差异巨大的合金基体和增强相两相材料。多尺度有限元法是一种既能在大尺度上求解问题、又能反映小尺度信息的方法，可以显著提高计算精度并在宏观和细观尺度上较好地预测非均质材料的力学特性。文献[16,17]采用单向多尺度方法建立了局部细观模型，利用子模型方法将宏观响应量传递给细观模型进行应力及损伤分析，可用较小的计算量获得较高精度的局部应力。

本工作运用实验和模拟计算分析了31%B4C/6061Al (质量分数)复合材料热压缩过程中的断裂损伤模型，考虑了温度和应变率对裂纹开裂的影响，确定了GTN (Gurson-Tvergaard-Needleman)损伤模型中的材料常数，并采用单向多尺度有限元法分析了裂纹开裂的细观机制。

1 损伤模型

通过模拟仿真方法研究材料的断裂损伤行为时，损伤模型的选取是至关重要的，只有恰当地选取损伤模型，才能保证材料断裂后计算结果的正确性。通常情况下，材料压缩过程中的断裂模型主要有剪切断裂(shear fracture)[18,19,20,21]、J-C (Johnson-Cook) 断裂[22]和GTN断裂[23,24]模型。J-C损伤模型适用于高应变率切削仿真，因此，本工作主要考虑剪切损伤和GTN损伤模型。

1.1 剪切损伤模型

剪切损伤是由材料变形过程中内部剪切带的滑移引起的，因此剪切损伤模型在热压缩模拟过程中是值得考虑的。塑性变形单调递增的状态变量(WD)表示为[25]：

${?}_{\mathrm{D}}=\frac{{\overline{?}}_0^{\mathrm{p}}+\sum \mathrm{\Delta }{\overline{?}}^{\mathrm{p}}}{\mathrm{\Delta }{\overline{?}}_{\mathrm{f}}^{\mathrm{p}}}$(1)${?}_{\mathrm{s}}=\frac{\overline{?}+{?}_{\mathrm{s}}\times ?}{{?}_{\mathrm{m}\mathrm{a}\mathrm{x}}}$(2)

式中，${\overline{?}}^{\mathrm{p}}$为等效塑性应变；${\overline{?}}_0^{\mathrm{p}}$为等效塑性应变的初始值；$\sum \mathrm{\Delta }{\overline{?}}^{\mathrm{p}}$为等效塑性应变增量；${\overline{?}}_{\mathrm{f}}^{\mathrm{p}}$为失效应变；$\overline{?}$为von Mises应力；p 为静水压力；τmax为最大剪应力；Ks为材料系数，通常为0.3[20]；θs为剪应力比。当WD≥1时，材料就会出现损伤[25]。

1.2 GTN损伤模型

GTN损伤模型是基于Gurson[26]提出的多孔材料理论演变而来的。Gurson[26]提出，在塑性变形过程中，材料的微观组织会出现很多随机分布的小孔洞，在材料加工变形中，这些小孔洞会不断的生长、变大，最后聚集形成大孔洞直到材料断裂。Needleman和Tvergaard[27]考虑了材料变形过程中孔洞之间的相互作用对材料断裂的影响，改进了多孔材料理论，从而形成了GTN损伤模型。其中材料的屈服函数(Φ)如下[27]：

$?={(\frac{\overline{?}}{{?}_{\mathrm{y}}})}^2+2{?}_1{?}^{\mathrm{*}}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}(-\frac{3{?}_2{?}_{\mathrm{m}}}{2{?}_{\mathrm{y}}})-1-{?}_3({?}^{\mathrm{*}}{)}^2=0$(3)

式中，σy为材料的屈服应力，q1、q2和q3为反映孔洞相互作用的常数，σm为平均应力，f *为孔洞合并时失去应力承载能力的函数，是关于孔洞体积分数(f)来进行定义：

${?}^{\mathrm{*}}=\left\{\begin{array}{l}?\\ {?}_{\mathrm{c}}+\frac{{?}_{\mathrm{u}}-{?}_{\mathrm{c}}}{{?}_{\mathrm{f}}-{?}_{\mathrm{c}}}(?-{?}_{\mathrm{c}})\\ {?}_{\mathrm{f}}\end{array}\right.$$\begin{array}{l}(?\le {?}_{\mathrm{c}})\\ ({?}_{\mathrm{c}}<?<{?}_{\mathrm{f}})\\ (?\ge {?}_{\mathrm{f}})\end{array}$(4)

式中，fc为临界孔洞体积分数，ff为完全失效时的孔洞体积分数，fu为平衡系数。

在塑性变形过程中，$?$的改变是由于孔洞的增长和新孔洞的形成共同导致的，具体演化过程如下式所示：

$\dot{?}={\dot{?}}_{\mathrm{g}}+{\dot{?}}_{\mathrm{n}}$(5)${\dot{?}}_{\mathrm{g}}=(1-?){\dot{?}}_{\mathrm{k}\mathrm{k}}^{\mathrm{p}}:\mathit{?}$(6)${\dot{?}}_{\mathrm{n}}=\frac{{?}_{\mathrm{N}}}{{?}_{\mathrm{N}}\sqrt[]{2\mathrm{\pi }}}\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{1}{2}{(\frac{{\overline{?}}^{\mathrm{p}}-{?}_{\mathrm{N}}}{{?}_{\mathrm{N}}})}^2\right]{\dot{\overline{?}}}^{\mathrm{p}}$(7)

式中，$\dot{?}$为孔洞体积分数的变化率，${\dot{?}}_{\mathrm{g}}$为孔洞增长和控制塑性应变增量张量引起的孔洞体积分数增量，${\dot{?}}_{\mathrm{n}}$为孔洞形核所引起的孔洞体积分数增量，${\dot{?}}_{\mathrm{k}\mathrm{k}}^{\mathrm{p}}$为基体等效塑性应变率，${\dot{\overline{?}}}^{\mathrm{p}}$为等效塑性应变率，I为二阶单位张量，fN为空洞形核的体积分数，SN为应变的标准偏差，εN为材料的平均应变。

2 热压缩实验

实验材料为粉末冶金方法制备的31%B4C/6061Al复合材料，B4C颗粒平均尺寸为5~20 μm，其初始显微组织如图1所示。6061Al合金的主要化学成分(质量分数，%)为：Fe 0.70，Si 0.80，Mn 0.15，Cr 0.35，Mg 1.20，Zn0.25，Al 余量。热压缩实验试样尺寸为直径8 mm×12 mm的圆柱体，实验温度分别为375、425、475和525 ℃，应变率为0.01、0.1、1和10 s-1。压缩实验在Gleeble 3800 热力模拟试验机上进行，在压缩实验过程中，Gleeble 3800热模拟机微处理器利用标准的方程自动采集实验数据和曲线。热压缩后在线切割机上将试样沿垂直加载轴方向切割，并利用MEF4A型万能光学显微镜(OM)观察并测量裂纹长度。

图1

图1   31%B4C/6061Al 复合材料的初始显微组织的OM像

Fig.1   OM image of initial microstructure of 31%B4C/6061Al composite

3 有限元模拟

为保证有限元仿真与实验结果的一致性，在ABAQUS有限元软件中建立了与实验试样尺寸相同的三维非线性热力耦合有限元模型，如图2所示。模型中上下模具定义成解析刚体，仿真计算选用动态显式(ABAQUS/Explicit)求解器，网格类型采用三维八节点六面体减缩积分单元C3D8RT。热压缩模拟试样的材料常数见表1，本构关系见文献[11]，上下模具与试样之间的摩擦系数为0.3[28]。解析刚体的约束和载荷通过参考点(reference point)定义。由于在实验中采用的是单向压缩，因此，将下模具采用完全固定的约束，而在上模具施加不同应变率所对应的速率(v)为：

图2

图2   热压缩有限元模型

Fig.2   Finite element model for hot compression

表1   31%B4C/6061Al复合材料热物理性能

Table 1  Thermo-physical properties of 31%B4C/6061Al composite

Thermo-physical parameter	Value	Unit
Young's modulus (E)	136	GPa
Shear modulus of elasticity (G)	52.3	GPa
Specific heat (cp)	1.381	J·g−1·K−1
Thermal diffusivity	31.42	m2·s−1
Coefficient of thermal expansion (φ)	16.9×10−6	K−1
Poisson's ratio (μ)	0.3
Density (ρ)	2.64	g·m−3

新窗口打开| 下载CSV

$?=\frac{?}{?}=\frac{?}{?/\dot{?}}$(8)

式中，S为试样的压缩量，t为压缩时间，ε和$\dot{?}$为试样的应变和应变率。

4 结果与分析

4.1 裂纹形貌分析

图3所示为31%B4C/6061Al复合材料在应变率10 s-1、压下量为75%时，不同温度下的热压缩实验所得的裂纹形貌。从图中可以看出，热压缩后的试样出现了不同深度和宽度的裂纹，而且裂纹都是沿着平行于加载方向分布的。随着实验温度的升高，裂纹的深度和宽度有所下降，这也进一步验证了随着热变形温度的升高，31%B4C/6061Al复合材料的可加工性提高。

图3

图3   应变率10 s-1、压下量为75%时，31%B4C/6061Al复合材料热压缩后不同温度下的裂纹形貌

Fig.3   Crack morphologies of 31%B4C/6061Al composite after hot compression at 375 ℃ (a), 425 ℃ (b), 475 ℃ (c) and 525 ℃ (d) under strain rate of 10 s-1 and reduction of 75%

图4所示为采用剪切损伤模型模拟计算得到的应变率为10 s-1、压下量为27%时，不同温度下31%B4C/6061Al复合材料热压缩后的裂纹形貌。可以看出，当热压温度为375 ℃时，圆柱试样上出现了2条约45°方向的斜裂纹。由于上下模具与试样的摩擦作用，试样在压缩过程中除了受与加载方向成45°方向的剪应力外，还有较小的正压力，因此，试样出现了沿45°方向的剪切断裂和沿压缩方向的局部断裂。通过与图3的实验结果比较，可以发现剪切损伤模型计算所得的裂纹形貌与实验完全不符，说明剪切损伤模型不能预测31%B4C/6061Al复合材料热压过程的断裂。

图4

图4   应变率10 s-1、压下量为27%时，由剪切损伤模型计算所得不同温度下31%B4C/6061Al复合材料的裂纹形貌

Fig.4   Crack morphologies of 31%B4C/6061Al composite calculated by shear fracture model at 375 ℃ (a), 425 ℃ (b), 475 ℃ (c) and 525 ℃ (d) under strain rate of 10 s-1 and reduction of 27%

图5所示为采用GTN损伤模型计算得到的应变率为10 s-1时，不同温度下31%B4C/6061Al复合材料热压缩后的裂纹形貌。可以看出，模拟计算所得裂纹形貌与实验结果相同。模拟中发现，采用GTN损伤模型，在压下量较小时，试样表面并没有出现裂纹，这与实验观测到的现象一致。除此之外，可以明显地发现，随着热压温度的升高，试样表面的裂纹变浅、宽度变窄，这也与实验所得结果相吻合。因此，GTN损伤模型可以很好地预测31%B4C/6061Al复合材料热压缩过程的断裂行为。

图5

图5   应变率10 s-1时由GTN损伤模型计算所得不同温度下31%B4C/6061Al复合材料的裂纹形貌

Fig.5   Crack morphologies of 31%B4C/6061Al composite calculated by GTN model at 375 ℃ (a), 425 ℃ (b), 475 ℃ (c) and 525 ℃ (d) under strain rate of 10 s-1

4.2 GTN损伤模型参数的确定

为了准确预测31%B4C/6061Al复合材料热压缩过程的断裂特性，经过多次试算发现GTN模型中损伤参数εN、SN、fN、fc和ff对裂纹特性影响较大。f0为复合材料内部的初始孔洞体积分数，由于基体和增强相之间界面及基体内部的材料缺陷会使初始孔洞体积分数不为零。因此，比较不同压缩条件下实验与模拟结果，通过对这些损伤参数的多次调整，最终确定了31%B4C/6061Al复合材料的GTN损伤模型参数为q1=1.5，q2=1，q3=2.25，f0=0.0025，fc=0.0065，ff=0.0098，fN=0.005，εN=0.3，SN=0.08，其中q1、q2、q3值采用Abendroth等[29]和Benseddiq等[30]的研究结果，f0值采用文献[23]的研究结果。

图6显示了应变率为10 s-1时不同温度下GTN损伤模型计算与实验裂纹深度对比。GTN损伤模型的裂纹形貌通过ABAQUS软件的视图切面功能获得，每一个图形都是从热压缩试样中间切开，并用测量工具测出裂纹深度，如图6a~d所示。实验所得的裂纹是将试样沿垂直加载方向切开，在OM下测量裂纹深度，如图6e~h所示。可以看出，GTN损伤模型计算与实验裂纹形貌和深度非常相似，而且，随着热压温度的升高，裂纹的深度都逐渐减小，模拟的误差在15%之内。

图6

图6   应变率为10 s-1时不同温度下GTN损伤模型计算与实验裂纹深度对比

Fig.6   Comparisons of crack depth calculated by GTN model (a~d) and experimental results (e~h) at 375 ℃ (a, e), 425 ℃ (b, f), 475 ℃ (c, g) and 525 ℃ (d, h) under strain rate of 10 s-1

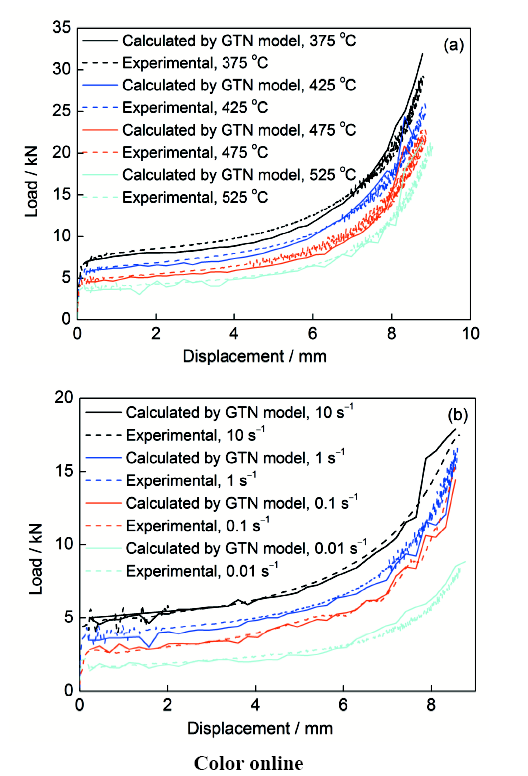
图7a给出了31%B4C/6061Al复合材料在应变率为10 s-1时，不同温度下GTN损伤模型计算与实验载荷-位移曲线的比较，图7b显示了525 ℃时不同应变率下GTN损伤模型计算与实验载荷-位移曲线的比较。可以看出，随着温度的升高和应变率的降低，材料的流变应力逐渐下降，模拟曲线和实验曲线吻合很好。在不同热压缩条件下, 31%B4C/6061Al复合材料的载荷-位移曲线变化规律相似。在变形的初始阶段，即弹性阶段，载荷随位移的增加而急剧升高；变形中期，载荷曲线随位移的增加变化很平缓；当位移为6 mm左右(压下量为试样高度的二分之一)时，载荷随位移的增加又快速增大。变形中期载荷变化平缓是由于热变形过程中，硬化机理(如应变硬化)以及软化机理(如动态回复、动态再结晶)同时产生且相互作用[31]。

图7

图7   不同温度和应变率下GTN损伤模型与实验所得热压缩过程中载荷-位移曲线的比较

Fig.7   Comparisons of load-displacement curves be-tween experimental and calculated by GTN model during hot compression at strain rate of 10 s-1 (a) and 425 ℃ (b)

通过比较可以发现，采用GTN损伤模型计算的31%B4C/6061Al复合材料热压裂纹形貌、尺寸及载荷-位移曲线与实验所得结果高度吻合。因此，本工作所求解的31%B4C/6061Al复合材料GTN损伤模型参数是准确可靠的，并且可以应用到该材料有限元数值模拟中。

4.3 多尺度法分析细观裂纹形成原因

采用单向多尺度有限元法分析31%B4C/6061Al复合材料的细观断裂特性时，由于热压缩实验的轴对称特性，选取如图8所示的9个位置。然后建立包含颗粒和基体的二维细观有限元模型，如图9所示。将上面宏观模拟得到的有效集合1~9的位移值提取出来输入到细观有限元模型中。

图8

图8   有限元模拟中特征位置的选取

Fig.8   Selections of feature positions in finite element simulation

图9

图9   31%B4C/6061Al复合材料二维细观有限元模型的建立

Fig.9   Establishment of 2D mesoscopic finite element model of 31%B4C/6061Al

(a) microstructure (b) local zooming (c) finite element model

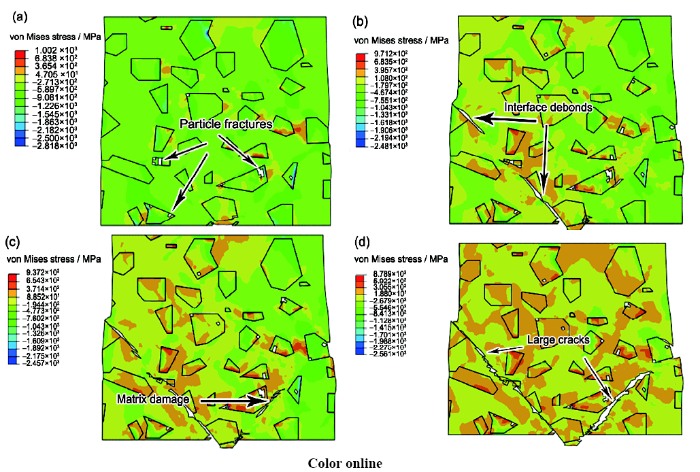
通过细观子模型的计算发现，随着计算时间的延长，只有集合6和9二维细观有限元模型中出现了裂纹，其它位置只是发生了不同程度的变形。图10显示了沿压缩方向不同时刻的等效应力图。从图10a可以看出，随着压下量的增加，B4C颗粒发生了脆性断裂，而且断裂的位置一般出现在颗粒的尖角处，这是由于应力集中的缘故。随着压下量的增加，基体和颗粒的界面出现了脱黏，如图10b所示，然后基体也出现了不同程度的损伤，如图10c所示。小裂纹继续扩展、合并，最后形成2条长裂纹，如图10d所示。这也说明了31%B4C/6061Al复合材料热压缩过程中出现的裂纹是由细观结构中颗粒的脆性断裂、基体和界面的脱黏以及基体损伤导致的。

图10

图10   随压缩时间的延长，细观模型中裂纹的形成过程

Fig.10   Crack formation in mesoscopic model at time of 0.06 s (a), 0.062 s (b), 0.065 s (c) and 0.068 s (d)

5 结论

(1) 通过有限元分析与实验对比，剪切损伤模型不能预测31%B4C/6061Al复合材料热压缩开裂行为，GTN损伤模型能准确预测31%B4C/6061Al复合材料热压缩断裂行为。

(2) 通过比较不同压缩条件下实验与模拟结果，分析了压缩裂纹深度与载荷-位移曲线，确定了31%B4C/6061Al复合材料的GTN损伤参数，从而为该材料断裂模拟计算提供了可靠数据。

(3) 运用单向多尺度有限元法分析了B4C/6061Al复合材料热压缩过程的细观损伤机理，热压缩过程中出现的宏观裂纹是由细观结构中颗粒的脆性断裂、基体和界面的脱黏以及基体损伤导致的。

来源--金属学报