分享:UN核燃料烧结致密化过程的相场模拟
戚晓勇1,2, 柳文波 ,1,2, 何宗倍3, 王一帆3, 恽迪1,2
,1,2, 何宗倍3, 王一帆3, 恽迪1,2
1.
2.
3.
引入了平移和旋转等作用过程,建立了烧结致密化过程的相场模型,分析了平流通量刚体运动对烧结颈的形成、平衡二面角和烧结致密化过程的影响。模拟结果表明,引入平流通量刚体运动在烧结初期加快了烧结颈的形成,而在烧结后期作用不明显;烧结相场模型中是否引入平流通量不影响晶界平衡二面角的取值;致密化过程的气孔收缩分为3个阶段,分别是烧结初期的表面扩散主导阶段、平流通量取代表面扩散的阶段和致密化完成阶段;增大平移迁移率能加快致密化过程、增加致密化程度,但超过一定阈值后其作用达到饱和;颗粒完成致密化收缩后会形成稳定的三叉晶界(夹角120°),多晶UN烧结模拟形貌演化中三叉晶界的形成和气孔收缩致密化的行为与实验结果一致。
关键词:
UN燃料具有密度高、导热系数高、熔点高、辐照稳定性好、裂变气体释放率低和具有较高的事故容错率等优点,是轻水反应堆、快堆的候选燃料。UN的U密度为13.55 g/cm3 [1],显著高于UO2的U密度(9.75 g/cm3)[2],采用燃料组件较小的UN燃料可以使得轻水反应堆的功率显著提高。室温下UN的导热系数为20.6 W/(m·K),显著高于UO2的导热系数(3.5 W/(m·K)),采用高导热系数的UN燃料可以显著降低燃料温度,使得在过渡条件下拥有较大的安全裕度[3]。然而,目前UN燃料芯块烧结制造工艺仍不成熟,其中一个重要原因是UN中的共价键比例高,烧结致密化较为困难[4]。由于UN在高温下易分解,烧结温度提高和添加剂引入的限制,导致传统的烧结方法难以使芯块达到较高的致密度。此外,不同温度和燃耗的反应堆设计需要不同密度、孔隙率和几何形状的UN球团,孔隙率较低的高致密化UN颗粒可以强化燃料结构和延缓裂变气体释放[3]。因此,研究UN球团烧结特性、微观组织对于指导UN烧结具有重要的意义。
近年来,国内外学者做了许多不同温度、不同时间、多种烧结方式下的UN烧结致密化实验[3~9]。实验结果主要集中在烧结后晶粒尺寸、致密化球团的孔隙率以及显微组织控制方面。尹邦跃和屈哲昊[4]的热压烧结实验结果表明,1550℃烧结温度和2 h烧结时间下真空热压烧结UN芯块的致密度很高,晶粒细小均匀,平均尺寸≤ 10 μm。Muta等[6]对比了传统热压烧结与放电等离子体烧结(SPS)制备的样品扫描电镜(SEM)像,结果表明,传统烧结方法制备的样品具有较大的孔隙率,大部分气孔存在于晶界;SPS方法制备的样品中仅观察到很小的晶内孔隙,较低的烧结温度抑制了晶粒和气孔的生长,气孔的尺寸和分布与烧结条件无关。Malkki等[7]采用SPS方法在1650℃烧结温度和3 min烧结时间下得到孔隙率为0.17%的球团密度,并与Muta等[6]的数据进行比较得出结论:在颗粒尺寸接近的条件下,烧结温度是决定最终密度的因素。烧结在实质上是颗粒表面自由能减少的固态扩散过程,其扩散机制主要分为表面扩散(空位和原子沿颗粒表面)、晶界扩散、体积扩散(晶格扩散)等,以及它们之间的耦合作用[10~12]。烧结过程的物质迁移包括表面迁移和颗粒平移旋转的刚体运动[13],2种迁移机制的区别在于能否完成烧结气孔致密化。表面迁移机制的物质迁移只存在于表面,主要表现为烧结颈的形成与生长,不涉及空位的传输;颗粒刚体运动的物质迁移存在于表面和晶界,主要表现为促进烧结颈增长,颗粒靠拢气孔致密化,涉及到空位的传输。然而,由于现有实验条件的局限性,难以对烧结微观组织致密化过程进行观测,这也间接导致了无法很好解释烧结致密化过程的机理。因此,采用计算机模拟UN烧结过程的孔隙演化与致密化过程具有十分重要的现实意义。
最近,Chen和Zhao[14]总结了利用相场法设计材料以获得最佳性能的热力学基础和研究进展。Ishii等[15]提出了一种新的数据同化方法来估算固相烧结材料的参数。陶瓷烧结过程的相场研究方面已经取得了一些成果[16~20]。Ahmed等[16]开发出一种考虑曲率驱动晶界运动和表面扩散引起孔隙迁移的新型相场模型,研究了孔隙度对UO2中晶粒长大动力学的影响。Kundin等[17]提出了2种类型的模型描述孔隙与晶界的相互作用,研究了孔隙动力学对陶瓷材料晶粒尺寸演化的影响。H?tzer等[18]提出了一种考虑表面扩散和晶界扩散的相场模型描述Al2O3固态烧结过程。然而,表面扩散模型并不能模拟UN烧结后期的致密化过程,烧结致密化的机理有待进一步澄清。气孔致密化过程包含平移旋转刚体运动与晶界扩散,刚体运动的驱动力来源于晶界吸收作用,过饱和的空位被晶界吸收产生局部驱动力,将相邻颗粒通过平移旋转刚体运动相互靠拢[13,19]。颗粒的平移和旋转直接减小颗粒之间的距离,促进气孔完成致密化。因此,考虑颗粒之间的平移旋转刚体运动对晶界和致密化的影响,可以更好地了解烧结过程的物质传输机理,为烧结过程提供指导。
本工作在表面扩散相场模型[16]的基础上对扩散方程进行了修正,添加了含有平移旋转刚体运动的相互作用项,采用相场理论模拟了UN粉末在表面扩散与平移旋转刚体运动共同作用下颗粒间烧结颈的长大以及气孔的演化过程,研究了UN粉末烧结颈的形成过程、气孔收缩致密化的过程、形成稳定三叉晶界的过程以及多晶粒烧结过程,模拟结果与实验观察结果符合较好。
1 相场模型
1.1 相场变量
本模型通过引入与结构相关的一系列取向场变量η1( r, t), η2( r, t), …, ηp ( r, t)和浓度场变量ρ( r, t)来表述不同取向的晶粒相和气孔相,它们是空间坐标( r )与时间(t)的连续函数。其中,ηi (i = 1, 2, …, p)为非保守型相场变量,用来描述多晶中不同晶粒的取向,第i个晶粒内部ηi 的取值为1,其余p - 1个取值为0;ρ( r, t)为保守型相场变量,在晶粒相取值为1,在气孔相取值为0。已有研究[20]表明,当晶粒个数p > 32时,晶粒组织演变对p取值的依赖性可以忽略。
1.2 自由能密度泛函数
本工作烧结相场模型的总自由能泛函数F采用以下形式[21]:
式中,第1项f表示局部自由能密度函数;第2项和第3项为梯度自由能,分别表示气孔表面和晶界处的额外自由能;κρ 和κη 代表梯度能系数,取决于材料气孔表面和晶界处的能量和宽度,J/m;V为空间体积。
本工作采取的f表达式如下[22]:
式中,A和B为与材料气孔表面和晶界处能量和宽度有关的物理参数,J/m3;方程右侧第1项为双势阱函数,在晶粒内部与气孔内部取得平衡值;方程右侧方括号中为多势阱函数,在晶粒内部取得平衡值。本工作所采用的自由能泛函数能够保证在各个晶粒内部和气孔相的内部取得p + 1个极小值。
F中各常数与材料的物理参数之间的关系为[23]:
式中,γgb和γs分别为材料的比晶界能和比表面能,J/m2;δ为扩散界面的宽度,m。
1.3 动力学演化方程
假设烧结过程的质量是守恒的,为了描述烧结过程的气孔收缩和致密化,在演化动力学Cahn-Hilliard方程[21]中引入平流通量项。因此,ρ的演化方程为:
式中, vadv( r )为平流速度场,描述了通过刚体局部体积元素运动进行的质量传输。在 vadv( r )计算中,假设空位是系统中唯一存在的点缺陷类型,晶界和自由表面充当空位的有效源和汇。图1为烧结模拟中空位扩散示意图,表示烧结过程中空位从凹面区域扩散到凸面区域。
图1
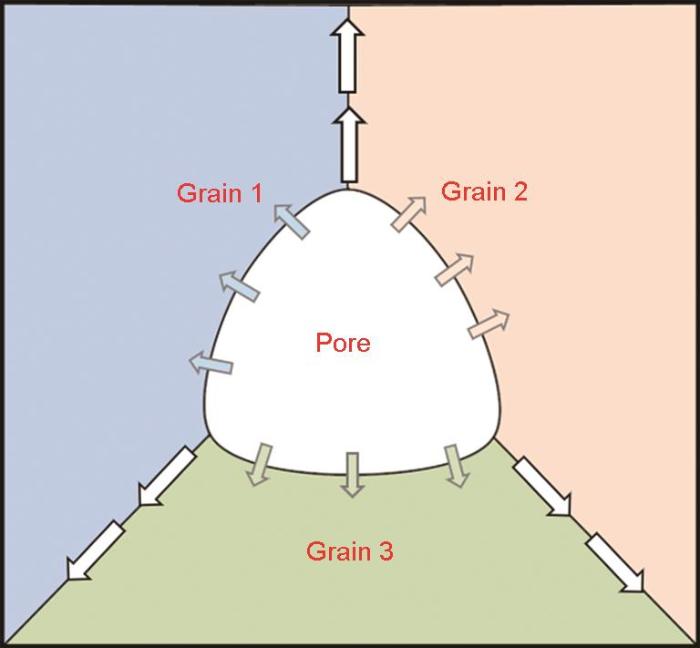
图1 烧结模拟中空位扩散示意图
Fig.1 Schematic of vacancy diffusion simulated in sintering simulation (Arrows show the paths of vacancy diffusion along free surfaces and grain boundaries)
M 为迁移率张量函数,表达形式为[23]:
式中,νm为摩尔体积;R为气体常数;T为温度; Ds为表面扩散系数张量;Ds为表面扩散率,取决于材料的性质; T s为表面投影张量,保证表面扩散在晶粒与气孔接触的表面切线方向; I 为单位张量;符号⊗为张量积; ns为垂直于曲面的单位法向量。
ηi 的演化动力学方程由Allen-Cahn方程[21]引入平流通量项后表示为:
式中, vadvi ( r )为 r 位置处晶粒i的平流速度;L为表征晶界迁移率的系数,在各向同性假设下为常数,与材料的具体性质关系如下[24]:
式中,Mb为晶界迁移率;Dgb为晶界扩散率,取决于材料的性质。
根据
为了直观地表征烧结过程,本工作中可视化变量φ为[20]:
1.4 平流速度场 vadv(r)
烧结过程中粒子的刚体运动由平移和转动2部分组成, vadv( r )表示为[22]:
式中, vti ( r )为在 r 位置处晶粒i的平移速度,表达式为[22]:
式中,mt为平移迁移率,m2/s;Vi 为晶粒i的体积;积分项为作用在晶粒i质心上的合力;κF为质量密度相对于在晶界平衡值变化的刚度系数,本工作取κF = 100;常数ρ0为晶界质量密度的平衡值,本工作取ρ0 = 0.98;r为空间位置;函数fV 用来识别2颗粒晶界之间的区域,表达式为:
式中,c*为晶界阈值。
vri ( r )为在 r 位置处晶粒i的旋转速度,表达式为[22]:
式中,mr为转动迁移率,m2/s; Ti 为作用在晶粒i的扭矩,表达式为:
式中, rci 为晶粒i质心的位置,表达式为:
2 无量纲化处理
无量纲化后的动力学方程与量纲控制方程具有相同的形式,可以在不改变驱动力的情况下缩放模型参数,将模拟的数量级统一,减小计算误差。本工作相场模型的变量与参数采用无量纲形式进行描述。
根据
由此可得无量纲迁移率张量
根据
由此可得无量纲化迁移系数
本工作取t* = 1 / (Lε*),ε* = B;则
根据所选取的参考物理量,无量纲迁移率张量
本工作利用相场模型对UN陶瓷粉末在1823 K温度下的烧结过程进行了数值模拟,模拟中用到的UN物理参数如表1[26,27]所示。
Table 1
| Parameter | Value | Unit | Ref. |
|---|---|---|---|
| Ds | 7.5 × 10-12 | m2·s-1 | [26] |
| Dgb | 0.01Ds | m2·s-1 | |
| γs | 1.6 | J·m-2 | [27] |
| γgb | 0.8 | J·m-2 | [27] |
| δ | 6 | nm | [27] |
将UN的物理参数代入上述方程中,求得各无量纲参数的具体数值如表2所示。
表2 模拟中的无量纲参数
Table 2
| Parameter | Value | Parameter | Value |
|---|---|---|---|
|
|
17 |
|
30-100 |
|
|
1 |
|
1 |
|
|
6.75 |
|
1 |
|
|
20.25 | Δx = Δy | 1 |
|
|
6750 | Δt | 2 × 10-5 |
3 结果与讨论
3.1 2个颗粒烧结
本工作采用相场模型,模拟了双晶粒结构中UN陶瓷粉末烧结过程,将该相场模型的模拟结果与未加平流通量相场模型的模拟结果进行对比分析。所选模拟区域差分网格尺寸为150 × 150,选取周期性边界条件。分析平流通量对UN陶瓷粉末烧结组织演变过程、烧结颈形成、平衡二面角和致密化的影响。
3.1.1 烧结颈的形成
图2为未引入平流通量和引入平流通量2个等尺寸的圆形颗粒在烧结过程中的组织演变。其中颗粒的半径R = 30,与平流通量模型模拟相关的参数mt = 30,c* = 0.05,κF = 100,ρ0 = 0.98。从图2a~c与d~f对比可以看出,未引入平流通量的模拟烧结颈形成较慢,颗粒位置无明显移动;含有平流通量的模拟烧结颈的形成明显更快,颗粒位置发生移动,且稳态时烧结颈的长度更长。这与文献[19]给出的致密化特征十分吻合。烧结致密化取决于颗粒-孔隙相互作用,表面扩散主导的未加平流通量模型对烧结过程孔隙收缩没有贡献,所以烧结颈形成较慢;引入平流通量模型含有颗粒刚体运动过程,空位可以被晶界吸收湮灭,所以不仅促进烧结颈增长,且随着烧结颈生长,颗粒彼此接近。
图2
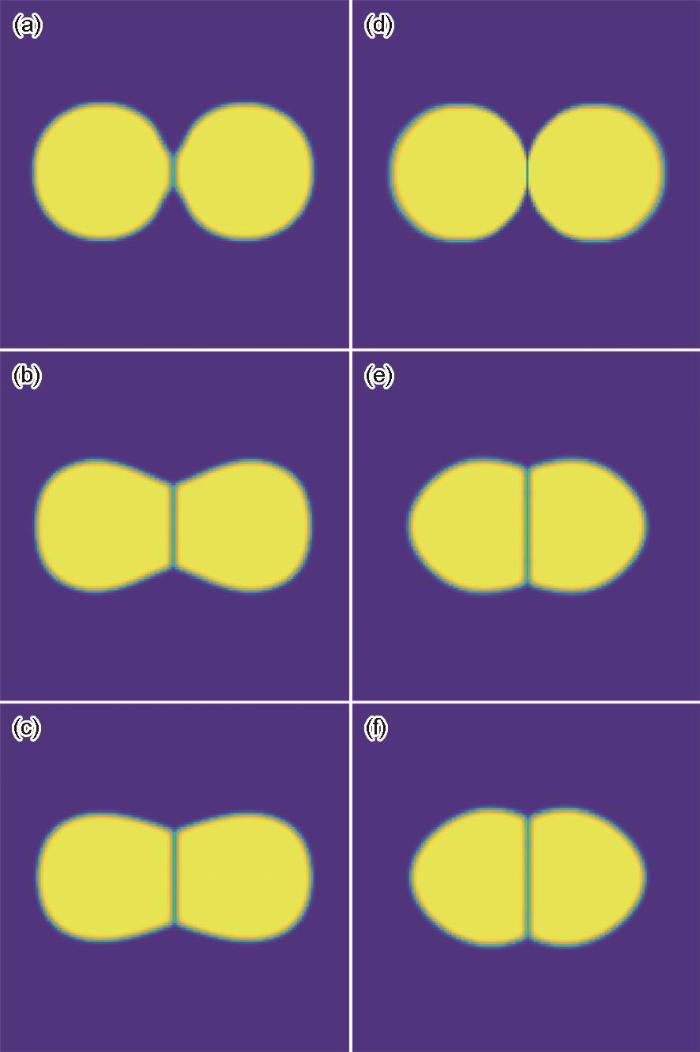
图2 平流通量对2个晶粒烧结形貌演化的影响
Fig.2 Simulated effects of advection flux on morphologies of two grains with the boundary between them by the phase-field methods of without (a-c) and with (d-f) advection flux (a, d) 2 × 104 step (b, e) 50 × 104 step (c, f) 100 × 104 step
图3为未引入平流通量与引入平流通量2种模拟数据的烧结颈对数增长曲线。可以看出,未引入平流通量模拟的烧结颈增长曲线近似为一条直线,斜率为0.21左右,满足烧结颈曲线增长规律[11]。引入平流通量模拟的烧结颈曲线分为3个时期:烧结前期,烧结颈的增长较快,斜率为0.68左右,这是因为颗粒的致密化移动使得烧结颈更快增长,从A点到B点平流通量起主要作用导致晶界宽度变窄;烧结中期,从B点到C点平流通量作用减弱,晶界宽度恢复,导致烧结颈长度下降;烧结后期,烧结颈不再增长且相比于未引入平流通量模型提前达到稳态,斜率为0.06左右。引入平流通量模型对烧结颈的形成在烧结前期作用较强,后期作用不明显。
图3

图3 平流通量对2个颗粒烧结颈增长曲线的影响
Fig.3 Logarithmic growth curves of particle sintered neck methods for without and with advection flux (l—neck length, t'—time step)
3.1.2 平衡二面角
界面性质在烧结过程中的气孔收缩、致密化和粗化过程中起关键作用。相邻的2个粒子在相界处由于表面能和晶界能形成一个平衡二面角(Ψ),在各向同性条件下,晶界处平衡二面角方程为[28]:
图4分别为未引入平流通量与引入平流通量2种烧结模型的平衡二面角,演化的总时间为2 × 106 step。本工作UN烧结晶界能与界面能的比值为γgb / γs = 0.5,对应计算值为Ψ = 150°。从图4可以看出,未引入平流通量模拟平衡二面角与理论计算值吻合较好,引入平流通量模拟最终平衡二面角与理论计算值有较小误差。证明了平流通量的引入会加快烧结颈的形成,但最终平衡二面角仍然不变,只由材料的特性所决定。这与只考虑表面扩散[29]的结论一致,平衡二面角与晶界能和界面能的比值保持一致。
图4
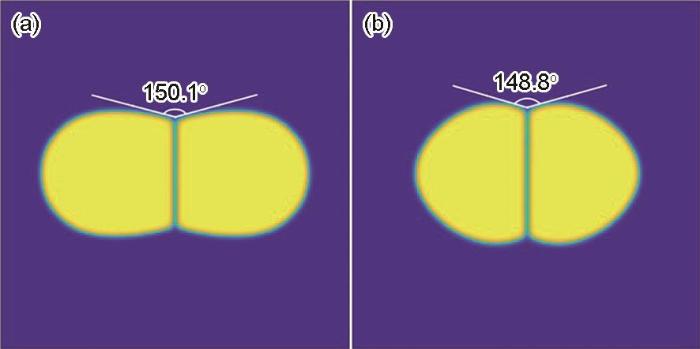
图4 平流通量对平衡二面角的影响
Fig.4 Simulated equilibrium dihedral angles by two sintering models
(a) without advection flux (b) with advection flux
3.1.3 晶界处气孔的收缩
图5为模拟双晶粒结构中晶界上含有气孔的致密化过程,将引入平流通量相场模型的模拟结果与未引入平流通量相场模型的模拟结果对比分析。从演化图像中可以看出,未引入平流通量模型晶界上的气孔稳定存在,引入平流通量模型晶界上的气孔逐渐收缩最终致密化。这与模型预期完全符合,表面扩散对致密化气孔收缩没有贡献。引入平流通量模型时2个颗粒晶界上气孔收缩随时间演化的曲线如图6所示。从曲线可以看出,平流通量作用分为2个阶段,演化前期由表面扩散主导,平流通量致密化气孔收缩作用较小,气孔收缩较慢;演化后期平流通量致密化主导,致密化气孔收缩较快。
图5
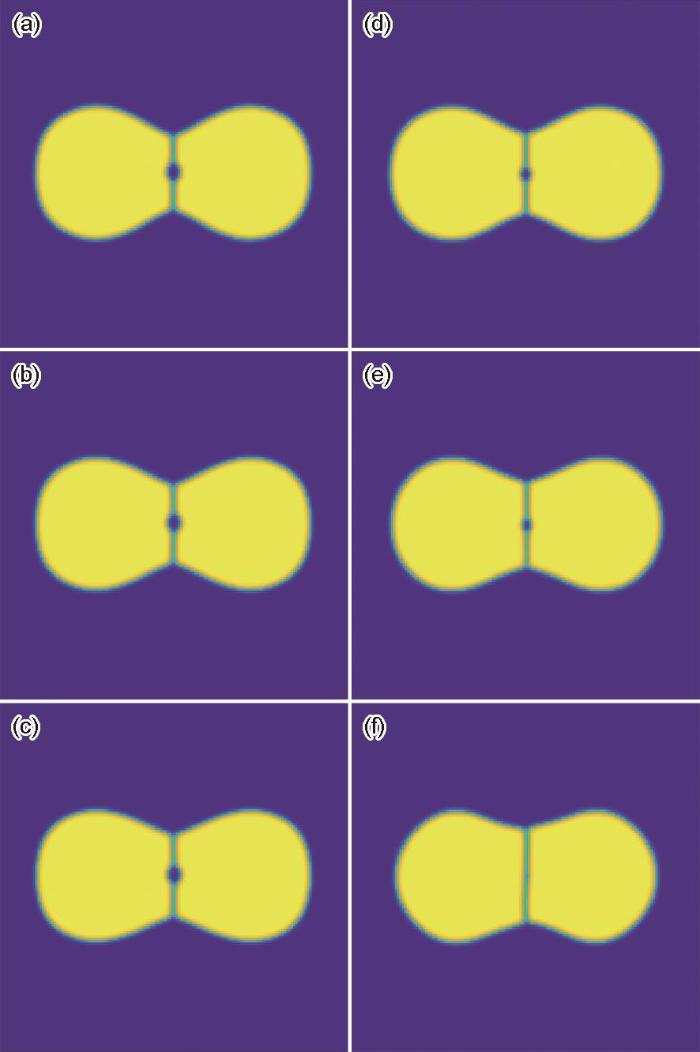
图5 平流通量对2个颗粒烧结过程中晶界气孔演化的影响
Fig.5 Simulated evolutions of a pore in the grain boundary between two particles by the phase-field methods of without (a-c) and with (d-f) advection flux (a, d) 10 × 104 step (b, e) 20 × 104 step (c, f) 30 × 104 step
图6
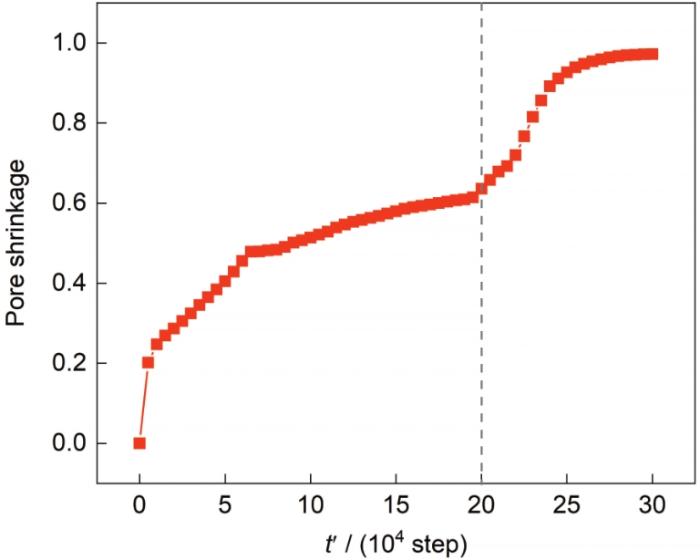
图6 平流通量作用下2个颗粒烧结过程中晶界的气孔收缩率
Fig.6 Simulated pore shrinkage curve of grain boundary between two particles by the advection flux model
3.2 致密化烧结
3.2.1 三叉晶界处的气孔收缩
图7为引入平流通量后,3个颗粒烧结的相场模拟结果。从图7b~d可以看出,颗粒发生了平移,逐渐完成致密化收缩。为了更加清楚直观地理解平流通量的作用,图8给出了与图7对应的平流通量的空间分布和时间演变,其中蓝绿色的部分表示平流通量的作用,越接近蓝色表示平流通量的作用越强。从图8b~d可以看出,平流通量作用于晶界与自由表面上,气孔收缩时平流通量逐渐增强,致密化完成后平流通量迅速减弱。
图7
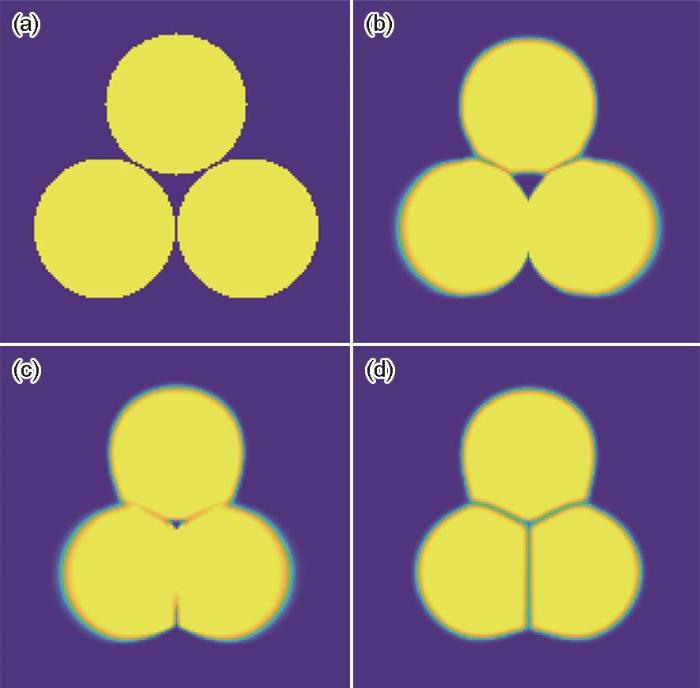
图7 引入平流通量后3个颗粒烧结时的形貌演化过程
Fig.7 Simulated evolutions of three particles by the phase-field methods of advection flux
(a) 0 step (b) 2 × 104 step
(c) 4 × 104 step (d) 6 × 104 step
图8

图8 3个颗粒烧结时形貌演化过程所对应的平流通量
Fig.8 Simulated evolutions of advection flux on morphologies of three particles (The blue-green part shows the effect of the advective flux, and the closer to the blue, the stronger the effect of the advective flux)
(a) 0 step (b) 2 × 104 step
(c) 4 × 104 step (d) 6 × 104 step
引入平流通量模型3个颗粒气孔收缩随时间演化的曲线如图9所示。结合图8平流通量的空间分布与时间演变,气孔收缩过程存在2个斜率的变化,可以将3个颗粒平流通量气孔收缩分为3个阶段:第1阶段,颗粒间形成颈缩;第2阶段,相邻颗粒通过平移运动导致粒子中心相互靠近;第3阶段,气孔完成收缩。在烧结过程中,涉及到2种机制:表面扩散机制和致密化平流通量机制。烧结初期,物质通过表面扩散主导传输,形成烧结颈;烧结中期烧结颈形成后,平流通量机制开始逐渐取代表面扩散主导,空位沿着晶界迁移,逐渐完成致密化过程;烧结后期最终致密化完成,达到稳态,平流通量迅速减弱。3个阶段斜率逐渐减小,表明随着烧结进行,烧结动力学逐渐减弱,平流通量随着烧结进行作用降低。
图9
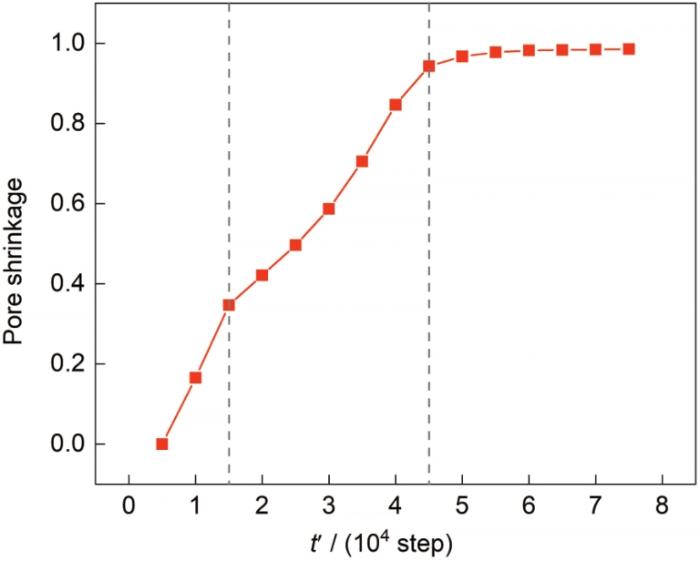
图9 平流通量作用下3个颗粒烧结时晶界上封闭气孔的收缩率
Fig.9 Simulated pore shrinkage curve of grain boundary among three particles by the advection flux model
3.2.2 平流通量平移分量对气孔收缩的影响
为进一步探究颗粒平移和旋转对致密化气孔收缩的影响,图10比较了不同平移迁移率下3个颗粒的气孔收缩。从图10可以明显看出,颗粒平移对致密化气孔收缩具有显著促进作用,随着mt的增大,致密化的速率增加,最终致密化的程度增加;当mt超过80时,致密化程度相对不变,最终完成致密化;当mt超过100时,致密化速率相对不变。与多相场(MPF)模型[30]的结果对比发现,本工作模拟颗粒平移迁移率对致密化影响更加明显。
图10
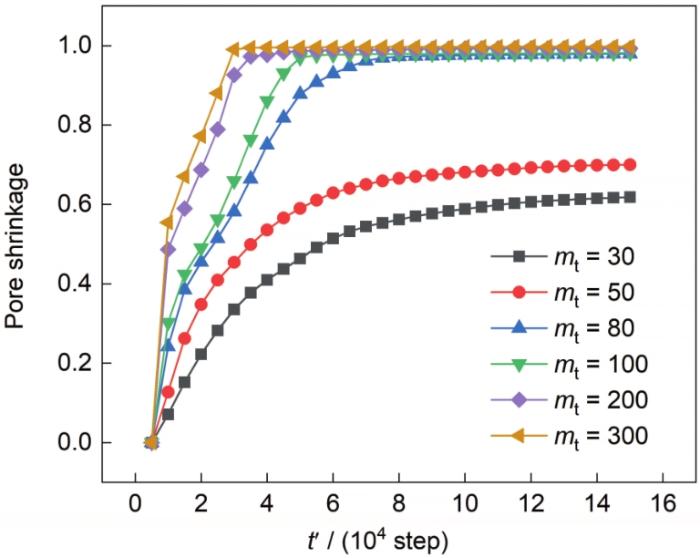
图10 不同平移迁移率下的气孔收缩率
Fig.10 Pore shrinkage curves for different translation mobilities (mt)
3.3 稳定三叉晶界的形成
图11为直径为60个格点的4个圆形颗粒形貌演变的相场模拟。可以看出,在演化初期,颗粒逐渐靠拢,气孔收缩完成致密化,形成角度为90°的四叉晶界;之后随着演化的进行,晶界发生变化,颗粒发生偏移,形成稳定的120°三叉晶界,这与大量的UN烧结实验[3~6,8,9]结果相吻合。这是因为演化中期晶界为不稳定状态(相邻晶界间的夹角处于90°),当相邻晶界演化至夹角为120°时,三叉晶界形状保持稳定。结合图7中3个颗粒烧结相场模拟结果,可以得出致密化气孔收缩完成趋向于形成稳定的120°三叉晶界。
图11
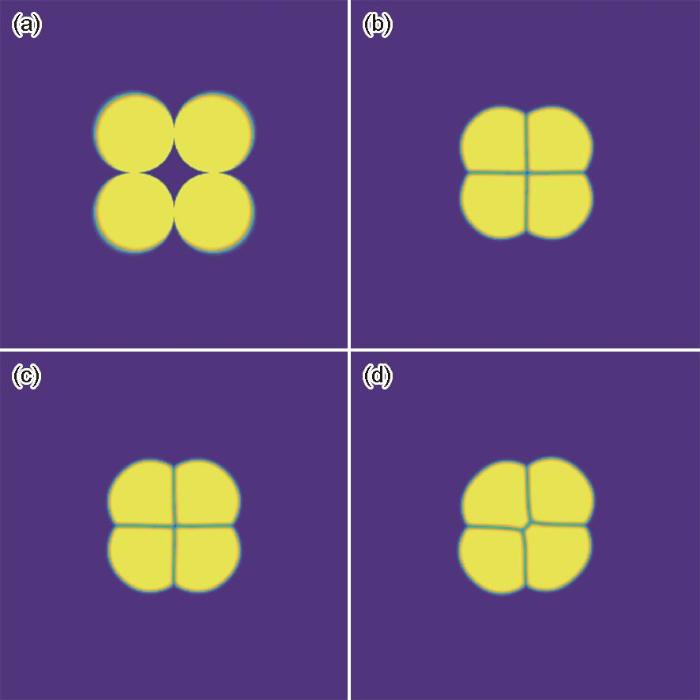
图11 引入平流通量后4个颗粒烧结时的形貌演化过程
Fig.11 Simulated evolutions of four particles by the phase-field methods of advection flux
(a) 1 × 104 step (b) 25 × 104 step
(c) 50 × 104 step (d) 100 × 104 step
3.4 多晶烧结过程
图12为颗粒尺寸单峰分布的多晶烧结相场模拟,模拟所采用的组织为30个不同尺寸的颗粒(图12a)。为与实验条件一致,选择颗粒的平均半径为150 nm,整个模拟区域的网格尺寸为256 × 256,采用耦合平流通量的致密化模型进行相场模拟。从图12可以看出,气孔对晶界移动起阻碍作用[31],气孔越大阻碍作用越强;相邻颗粒之间先形成烧结颈;颗粒之间形成气孔,气孔逐渐收缩,小气孔处晶界曲率较大、驱动力较强,优先完成致密化;致密化完成的部分逐渐形成稳定的120°三叉晶界。将本工作的演化模拟结果与真空热压烧结2 h的实验观察结果[4]进行对比可得,UN烧结形貌演化形成三叉晶界、气孔收缩致密化的行为与实验结果趋势一致。
图12
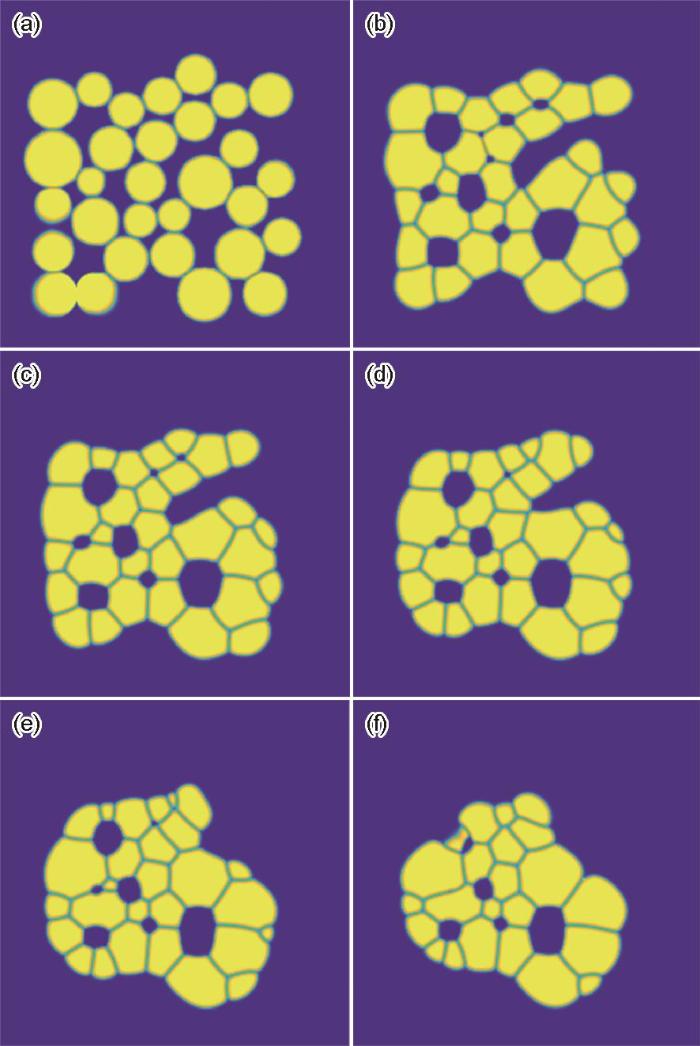
图12 多晶烧结形貌演化的相场模拟
Fig.12 Simulated evolutions of multi-grain by the phase-field methods with unimodal particle size distribution
(a) 1 × 104 step (b) 40 × 104 step
(c) 80 × 104 step (d) 120 × 104 step
(e) 160 × 104 step (f) 200 × 104 step
4 结论
(1) 引入了描述粒子刚体运动的平流通量作用项,建立了固相烧结致密化过程的相场模型,动态再现了UN晶粒烧结过程中内部气孔完成收缩的全过程。研究发现:引入平流通量模型对烧结颈的形成,在烧结前期作用较强,后期作用不明显;平流通量刚体运动的加入会加快烧结颈的形成,但最终平衡二面角的取值仍然不变,只由晶界能和界面能的比值所决定。
(2) 烧结过程中气孔的收缩分为3个阶段:初始阶段由于表面扩散占主导地位,颗粒间形成颈缩;中间阶段,平流通量刚体运动引起的致密化逐渐占据主导地位,相邻晶粒通过平移运动导致粒子中心相互靠近;最终阶段,气孔完成收缩,即致密化完成阶段。随着烧结进行,烧结动力学逐渐减弱,平流通量刚体运动随着烧结进行作用降低。随着平移迁移率(mt)的增大,致密化速率逐渐增加,最终致密化程度增加;mt超过100时致密化速率相对不变。
(3) 烧结相场模拟结果验证了相交120°的三叉晶界是能量上稳定的晶界,4个颗粒组成的晶界最终也演变成了稳定的三叉晶界;多晶UN颗粒烧结经历了烧结颈形成生长、气孔收缩致密化、稳定的三叉晶界形成等一系列微观过程;多晶烧结形成稳定的三叉晶界和气孔收缩致密化的现象与实验结果一致。
来源--金属学报





 沪公网安备31011202020290号
沪公网安备31011202020290号
