分享:铁素体晶间变形协调与硬化行为模拟研究
鉴于晶体塑性有限元法(CPFEM)在晶粒模型构造、取向设置和边界条件施加上的自由,对典型的铁素体-铁素体对称倾斜和扭转双晶模型实施不同应力状态下的变形模拟,分析应力状态和晶粒相对取向对晶界区应变分布和硬化行为的影响。结果表明,晶界区应变均匀程度由晶间滑移传递因子和滑移分切应力因子共同决定,晶粒的晶界区变形均匀程度与滑移传递因子正相关,主要由滑移传递因子控制晶间变形协调行为。然而,软取向晶粒(由应力状态和取向决定)的晶界区变形均匀,滑移传递因子对晶界区的应变协调不造成影响。此外,当滑移传递因子和滑移分切应力因子都很小时,易造成晶界区应变集中,使得晶间变形协调困难。因此,将滑移传递因子和滑移分切应力因子结合的晶间变形协调预测结果更为合理。双晶模型的流动应力与滑移分切应力因子负相关,晶界区非均匀变形易引发几何必需位错增殖,促进晶界处强化。
关键词:
晶界是晶粒间应力与应变的过渡区,也是晶粒变形协调的关键,决定着微孔洞和裂纹的形成与生长,对材料宏/微观力学性能有着重要影响。晶界也是位错运动的重要阻碍,位错在晶界区域的塞积会提高该区域的变形抗力,促使晶界区强化[1];当晶粒取向合适或者应力增大到一定程度时,位错可以穿过晶界,在另一侧晶粒形成新的位错。因而,晶界在实现晶粒变形协调以及促进材料强化方面起着重要作用。
Soer等[2,3]在纳米多晶的压痕实验中发现,加载曲线存在应变突跳现象,认为该现象与晶界屈服有关。位错在界面处塞积导致的高应力不断推动位错穿透晶界,当晶界处具备位错形核条件且应力达到临界值时界面屈服,该理论解释了纳米尺度的反Hall-Petch效应[4]。
晶界对位错的阻碍体现了其边界效应,Gurtin[5]在其所提出的单晶黏塑性梯度理论模型中给出了2种晶界处理方法,即夹持条件和自由条件。Okumura等[6]基于单晶黏塑性梯度理论进行了有限元模拟,获得了夹持条件和自由条件下均匀化的二维多晶模型的拉伸曲线,结果显示晶粒尺寸越小,材料硬化效应越强。针对理想晶界条件,Onho等[7]通过有限元法计算了拉伸和压缩载荷下的加载曲线,得到了二维多晶模型的Bauschinger特征。Ma等[8,9]改进了位错与晶界作用的有限元模型,认为单纯考虑微观扭转作用下的位错与晶界作用是不充分的,还需要考虑晶界处位错的热激活效应,且晶界处的强化与几何必需位错(geometrically necessary dislocation,GND)的动态效应紧密相关。Schiotz[10]模拟了多晶材料在拉伸作用下的变形情况,结果显示位错不断地从晶粒内部形核扩展,并在晶界处塞积,位错塞积提高了材料强度。
在晶间变形方面,Guo等[11]指出多晶体变形是非连续的,滑移线在晶界处停止传播,且存在大量的GND聚集。Livingston和Chalmers[12]研究了双晶铝晶界处的变形连续问题,并提出了晶界处位错堆积模型以预测变形所需附加滑移系。随后,基于对不锈钢的透射电镜(TEM)实验观察,Clark等[13]给出了经典的晶间滑移传递控制参数;基于类似的思路,Luster和Morris[14]定义了一个不依赖晶界面位向,可根据晶粒表层取向直接计算得到滑移传递控制参数。Sun等[15]对镁合金的研究也表明,晶界区域发生了明显的应变局部化,由Schmid因子与相邻晶粒的几何相容因子乘积构成的新判据与应变局部化的相关性最强,该值最能表征晶界附近的应变调节。Haouala等[16]基于实验和晶体塑性有限元法(CPFEM)分析了晶界在铝双晶强化中的作用,结果显示,晶界透明度的降低会使得应力响应提高,铝多晶材料拉伸时的晶间滑移传递依赖于晶界处开启的滑移系数目。
上述研究表明,将晶界视为绝对的可穿透或者不可穿透都是不准确的,相邻晶粒之间变形的传递(协调)是与其取向直接相关的。在取向适宜时,滑移系在晶界处可以很好地衔接,应变在晶界处易于协调,此时晶界趋向于一个透明或者可穿透界面;当取向不适于滑移传递时,此时滑移线在晶界处终止,界面倾向于一个不可穿透界面,且在界面处形成位错堆积,包括形成高密度的GND。然而,滑移系的激活同时取决于晶粒取向和应力状态,仅从晶粒取向不能准确描述晶间变形的协调性;晶界区变形由应力状态、取向和边界条件共同决定,各因素间彼此关联。此外,在实验中很难测量晶界的完整边界条件,难以控制晶界微区域所处应力状态,使得实验观测结果与理论预测[17]之间存在显著的离散性。
本工作以晶体塑性模型为基础,借助有限元法在晶粒取向定义和边界条件加载上的自由,对具有简单应力状态的铁素体-铁素体对称倾斜和扭转双晶模型进行变形模拟,探究多种应力状态下晶粒取向对晶界区变形的影响,揭示晶间变形协调和晶粒强化的内在控制因素。
1 研究方法
1.1 力学模型
本工作以Hutchinson[18]给出的指数形式的滑移剪切应变率(
式中,
式中,
式中,
式中,∇γ(β)为β滑移系的应变梯度向量; t (α)和 t (β)分别为滑移系α和β的滑移面法向向量,s(αβ) = d (α)· d (β),其中 d (α)和 d (β)为各自滑移方向。
1.2 双晶模型构建
本工作基于重位点阵(coincidence site lattice,CSL)[26]构建薄板状双晶有限元模型,并以垂直于晶界面的方向为长度方向以施加剪切、单轴拉伸和平面应变边界条件,如图1所示,图中O-xyz坐标系为加载坐标系。铁素体晶粒为bcc结构,分别以<100>、<110>和<111>为旋转轴构建符合CSL的对称倾斜晶界和扭转晶界的双晶模型,表1~3[27]为拥有较高重合点的3种对称倾斜/扭转晶界的晶体取向参数,双晶模型各应力状态对应的加载边界条件示意如图2所示,图中U示意位移加载的方向和位置。在晶体硬化方面,基于文献数据[21,22,28,29],模型硬化参数设定为:τc0 = 150 MPa;b = 2.5 × 10-10 m;μ = 80 GPa;
图1
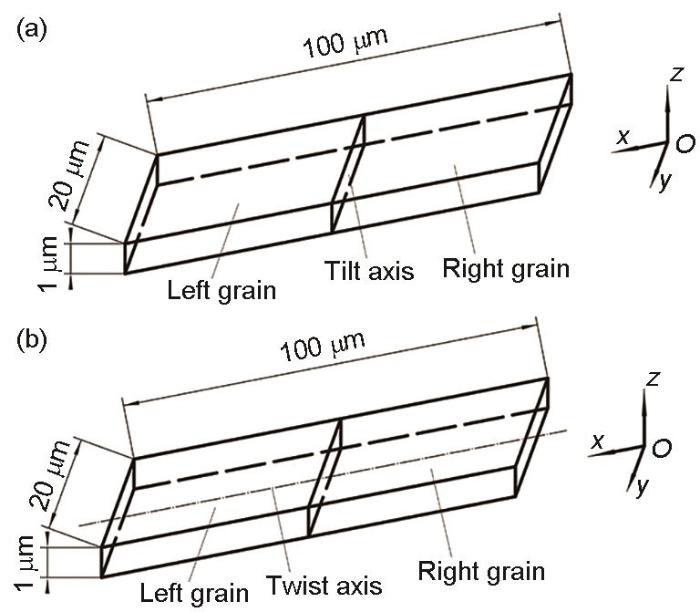
图1 双晶模型:对称倾斜晶界的双晶模型及扭转晶界的双晶模型
Fig.1 Symmetrically tilt bicrystal model (a) and twist bicrystal model (b)
表1 <100>对称倾斜/扭转晶界双晶模型晶粒取向[27]
Table 1
| Angle | Σ | Euler angle / (o) | |
|---|---|---|---|
| (axis: <100>) | Right grain | Left grain | |
| 0.00 | 1 | (0 0 0) | (0 0 0) |
| 16.26 | 25 | (180 8.13 180) | (0 8.13 0) |
| 22.62 | 13 | (180 11.31 180) | (0 11.31 0) |
| 28.07 | 17 | (180 14.04 180) | (0 14.04 0) |
| 36.87 | 5 | (180 18.44 180) | (0 18.44 0) |
| 53.13 | 5 | (180 26.57 180) | (0 26.57 0) |
| 61.93 | 17 | (180 30.97 180) | (0 30.97 0) |
| 67.38 | 13 | (180 33.69 180) | (0 33.69 0) |
| 73.74 | 25 | (180 36.87 180) | (0 36.87 0) |
| 90.00 | 1 | (180 45 180) | (0 45 0) |
表2 <110>对称倾斜/扭转晶界双晶模型取向[27]
Table 2
| Angle | Σ | Euler angle / (o) | |
|---|---|---|---|
| (axis: <110>) | Right grain | Left grain | |
| 0.00 | 1 | (0 0 0) | (0 0 0) |
| 26.53 | 19 | (-135 13.26 135) | (45 13.26 -45) |
| 31.59 | 27 | (-135 15.79 135) | (45 15.79 -45) |
| 38.94 | 9 | (-135 19.47 135) | (45 19.47 -45) |
| 50.48 | 11 | (-135 25.24 135) | (45 25.24 -45) |
| 70.53 | 3 | (-135 35.26 135) | (45 35.26 -45) |
| 109.47 | 3 | (-135 54.74 135) | (45 54.74 -45) |
| 129.52 | 11 | (-135 64.76 135) | (45 64.76 -45) |
| 141.06 | 9 | (-45 70.53 135) | (45 70.53 -45) |
| 148.41 | 27 | (-135 74.21 135) | (45 74.21 -45) |
| 180.00 | 1 | (-135 90 135) | (45 90 -45) |
表3 <111>对称倾斜/扭转晶界双晶模型取向[27]
Table 3
| Angle | Σ | Euler angle / (o) | |
|---|---|---|---|
| (axis: <111>) | Right grain | Left grain | |
| 0.00 | 1 | (0 0 0) | (0 0 0) |
| 13.17 | 19 | (-136.9 5.37 133.1) | (46.9 5.37 -43.1) |
| 21.79 | 7 | (-138.1 8.89 131.8) | (48.1 8.89 -41.8) |
| 27.80 | 13 | (-139.0 11.34 131.0) | (49.0 11.34 -41.0) |
| 32.20 | 13 | (-139.7 13.13 130.3) | (49.7 13.1 -40.3) |
| 38.21 | 7 | (-140.5 15.6 129.5) | (50.5 15.6 -39.5) |
| 46.82 | 19 | (-141.8 19.1 128.2) | (51.8 19.1 -38.2) |
| 60.00 | 1 | (-143.8 24.4 126.2) | (53.8 24.4 -36.2) |
图2

图2 双晶模型不同应力状态加载示意图
Fig.2 Schematics of bicrystal model loading in various stress states (U marks the displacement loading of the model)
(a) shear condition
(b) uniaxial tension condition
(c) plane strain condition
1.3 晶间变形协调参数计算
晶体的塑性变形以位错滑移为主要机制,因而晶界对晶粒变形的作用可归结于对滑移系开启以及滑移系与晶界作用的影响。Clark等[13]和Luster等[14]定义了由晶间滑移系几何位向表征的滑移传递因子m和m*,具体表达式为[17]:
式中,滑移系与晶界之间的关系定义为3组矢量之间的夹角,分别为:κ,两侧晶粒滑移系滑移方向间的夹角;
由晶体变形的运动学和动力学方程可知,各滑移系的剪切应变率与该滑移系的分切应力正相关,实际塑性变形过程中仅有少数处于优势取向的滑移系开启。取左右两侧晶粒滑移分切应力最大的4个滑移系计算滑移系间的滑移传递因子,并取大值表征晶界对变形传递的影响,m和m*的计算过程如下。
(1) 定义双晶模型的单位加载应力张量。滑移系的分切应力决定滑移应变率,且与取向和应力张量有关;由于Schmid因子会随着应力张量 σ 不同而发生变化,为确保不同应力状态下的最大切应力相同,本工作以单轴拉伸时最大切应力为拉伸应力1/2为基准,定义剪切、单轴拉伸和平面应变状态的单位应力张量,设定如下,剪切:
(2) 依据宏观加载状态和各晶粒取向,计算得到滑移系的分切应力
式中, P(α) = 0.5 × ( d (α)⊗t (α) + t (α) ⊗d (α))。
(3) 选择分切应力最大的4个滑移系作为激活滑移系参与计算,获得优势滑移系之间的m和m*。对于由单位应力张量计算得到的滑移分切应力,本工作称为滑移分切应力因子(resolve shear stress factor)。
2 结果与讨论
本节以晶界附近为关注区,以“距离晶界的距离”(后文简称“距离”)和“倾转角度”为变量,讨论晶界对晶粒变形、强化和位错密度变化的影响规律。以距晶界不同距离的各区域应变与模型施加应变的比值(应变比)描述晶界区的变形均匀程度,各区域的“应变比”越接近于1,晶界区变形越均匀。如图1所示模型,以晶界面为0点,分别取距离为1、2、3、5、8和10 μm对应区域的平均应变比来讨论晶界的影响范围。为分析应力状态的影响,不同应力状态双晶模型的等效加载应变均为0.12。本节首先以<110>对称倾斜双晶模型为例,对晶界区的变形与硬化特征予以详细分析;随后,汇总所有模型结果,揭示影响晶界区力学行为的内在因素。
以晶间倾转角度为变量,剪切、单轴拉伸和平面应变状态的应变比分布曲线如图3a1~c1所示,晶格完全重合的0°和180°取向各区域变形是均匀的,此时晶界不影响晶间变形协调;中间取向时的应变分布则体现出了显著的应力状态相关性。
图3
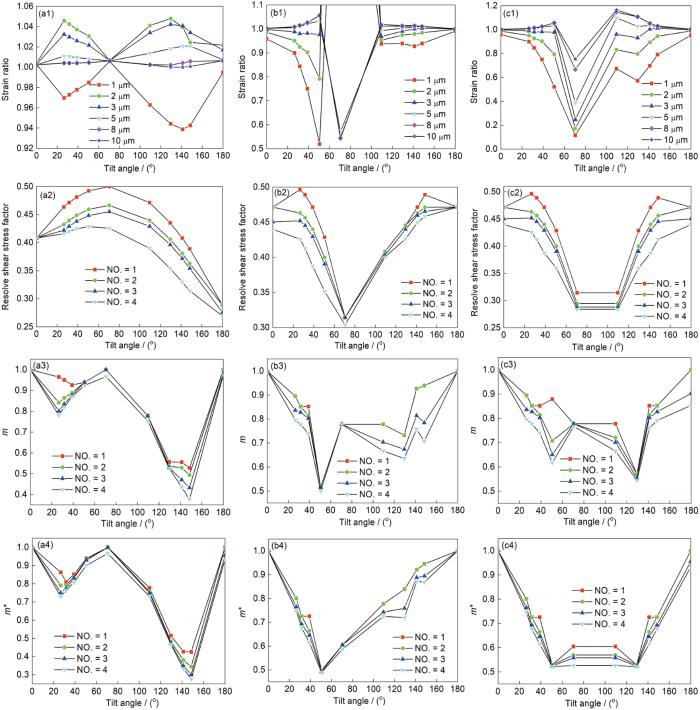
图3 不同应力状态下晶界区变形及其控制因素随倾转角度演化曲线
Fig.3 Grain boundary strain ratios (a1-c1), resolve shear stress factors (a2-c2), and slip transfer factors m (a3-c3) and m* (a4-c4) curves with tilt angle (NO. represents the number of participants in the average after sorting the corresponding parameters from largest to smallest)
(a1-a4) shear condition (b1-b4) uniaxial tension condition (c1-c4) plane strain condition
由图3a1可知,剪切状态下晶界区应变比曲线呈现W形,在倾转角度为0°、70.53°和180°时各区域应变比趋于1,晶界对两晶粒间的变形不产生影响;其开启滑移系的滑移分切应力因子呈先增大后减小趋势,且在70.53°时达到最大,如图3a2所示(图中NO.表示对应参数由大到小排序后,参与平均的数目)。另一方面,由开启滑移系相对位向关系计算的m和m*呈现了与应变分布相似的“W”形规律,如图3a3和a4所示。单轴拉伸状态下,晶界区应变比随倾角增大表现为先降低后升高的规律,并在50.48°和70.53°夹角时出现严重的应变集中现象(图4),此时晶界附近应变出现极大值,引起图3b1对应数据异常。对比滑移分切应力演化曲线(图3b2)可知,70.53°时晶粒取向陡然转为硬取向,晶粒变形困难,且此时滑移传递因子也处于较低数值(图3b3和b4),造成了该倾角时的应变集中。当倾角为50.48°时,晶粒处于滑移传递因子最低点(图3b3和b4),造成该倾角时出现应变集中现象。平面应力状态时,晶界附近(< 3 μm)应变比呈现先降低后上升现象,在70.53°附近时,滑移分切应力因子较低,仅为0.3左右,且滑移传递因子也处于低值区域(图3c3和c4),此时的晶界区应变仅为平均施加应变的20%左右,如图3c1所示。
图4
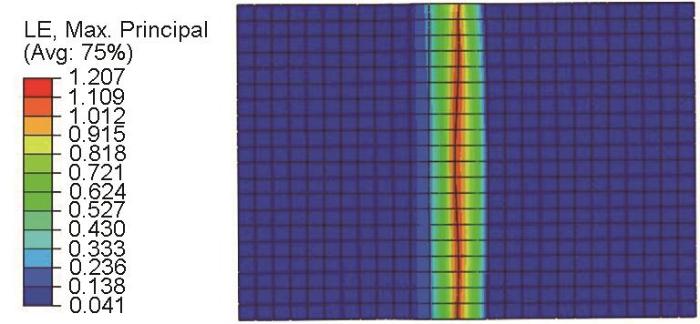
图4 <110>对称倾斜晶界(70.53°,(111)<110>Σ3)单轴拉伸时晶界区应变云图
Fig.4 Strain map of <110> axis symmetric tilt grain boundary with tilt angle is 70.53° (LE indicates logarithmic strain)
上述双晶变形的模拟结果与理论预测模型之间存在显著的相关性,当晶格重叠时(Σ = 1),不论何种应力状态,晶界区的变形都是均匀的,晶界的存在不产生任何影响。其他情况下,晶界区的变形行为与应力状态相关,晶界区变形均匀程度由滑移分切应力因子和滑移传递因子共同决定,2者中有1个处于显著低值时即可导致晶界区的应变集中现象;在滑移分切应力因子相近时,晶界区应变比与滑移传递因子正相关,如图3a1~a4中26.53°和141.06°的滑移传递系数和应变比均处于波谷位置。
晶体取向差异引起了晶界附近的非均匀变形,并以GND增殖的形式促进硬化,图5为晶界区GND密度随距离和倾转角度的演化曲线。
图5

图5 晶界区几何必需位错(GND)密度随距离和倾转角演化曲线
Fig.5 Geometrically necessary dislocation (GND) density curves with distance (a1-c1) and tilt angle (a2-c2) at grain boundary (a1, a2) shear condition (b1, b2) uniaxial tension condition (c1, c2) plane strain condition
以距离为变量时,各应力状态下晶界区的GND密度均随着距离的增大而迅速下降,其中剪切时靠近晶界的GND密度最高,随距离的下降速率也最大,如图5a1所示。上述现象是由剪切状态下晶界附近区域剧烈的应变梯度引起的(随着距离增大,应变比先迅速增大而后迅速减小,如图3a1所示)。另外,剪切时GND密度达到稳定所需的距离最短,为2~3 μm,单轴拉伸和平面应变则在5 μm以后才趋于稳定,小的过渡区进一步促使该区域产生更严重的应变梯度和高密度GND。单轴拉伸时(图5b1),倾转角度为70.53°时GND密度变化曲线严重偏离且远高于其他倾角,原因在于此时晶界附近出现应变集中(图4)使得该区域的应变梯度激增,导致GND密度计算结果过高。
对比图3a1和图5a2可知,剪切时的GND密度曲线呈现明显的“M”形,其对应的应变比曲线则呈“W”形,小应变比区域对应着高的GND密度,2者恰好相反。图3b1和图5b2显示(排除70.53°数据的影响),单轴拉伸时,倾角在0°~50.48°时,晶界区应变比逐渐下降,相应的GND密度逐渐升高;倾角在109.47°~180°时,应变比逐渐升高,相应的GND密度逐渐降低,2者仍然表现出显著的负相关特征。平面应变状态下,图5c2所示的GND密度与倾转角度的关系显示,在倾角为50.48°和109.47°时达到GND密度曲线的波峰,且倾角在109.47°~148.41°均有高密度的GND,对应着图3c1中的小应变比区域。特殊的是,倾角为70.53°时,尽管3 μm范围内的应变比最小,然而该范围内不同距离处的应变比接近(1、2和3 μm处均为0.2左右,如图3c3所示),应变比梯度小,因而GND密度较小。上述结果表明,GND密度的变化与应变比高度负相关,应变非均匀性严重的模型,GND密度高。
由上分析可知,晶间滑移传递因子和滑移分切应力因子共同影响晶界区变形。针对所有双晶模型,图6汇总了滑移传递因子和滑移分切应力因子与晶界区应变比关系的散点图,所示应变比为3 μm内平均值;图7为3 μm内流动应力与各晶粒滑移分切应力因子关系散点图。
图6

图6 晶界区应变比与滑移传递因子m、m*以及滑移分切应力因子散点图
Fig.6 Scatter maps of strain ratio with m (a1-c1), m* (a2-c2), and resolve shear stress factor (a3-c3)
(a1-a3) shear condition (b1-b3) uniaxial tension condition (c1-c3) plane strain condition
图7
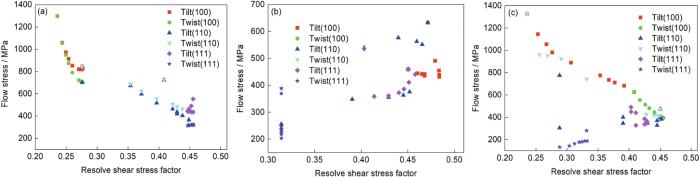
图7 晶界区流动应力与滑移分切应力因子关系
Fig.7 Flow stress vs resolve shear stress factor scatter maps of bicrystal model
(a) shear condition (b) uniaxial tension condition (c) plane strain condition
由图6a1和a2可知,剪切应力状态下,各模型晶界区应变差异与m和m*呈现显著的相关性。在m (m*) ≥ 0.5范围,晶界区应变比随着滑移传递因子的增大而近似线性增大,表明滑移传递因子大的模型(晶粒),其晶间变形易于协调,晶界区变形均匀。对于m (m*) < 0.5的区域,应变差异与滑移传递因子之间的相关性有所降低,该现象是由于滑移传递因子小的模型,晶粒一般处于硬取向(滑移分切应力因子较小,如图6a3所示),此时晶粒开启的滑移系较多,理论计算仅选择了4个优先开启的滑移系,因而得到的滑移传递因子不能完全准确地表征晶界区域的应变协调能力。另一方面,当滑移传递因子和滑移分切应力因子均很高时,晶界对两晶粒之间的变形传递几乎没有影响,晶界区应变均匀,例如Twist(111)和Tilt(111),如图6a1和a2所示。
单轴拉伸时的晶界区应变差异显著大于剪切状态(图6b1和a1),其变化范围分别为0.55~1和0.88~1,表明单轴拉伸时晶界区非均匀变形更为严重。由图6b1和b2可知,在不发生严重应变集中情况下,晶界区应变比与滑移传递因子存在正的相关性,随着滑移传递因子增大,晶界区应变比增大,变形非均匀性改善。但是,当晶粒处于软取向时,晶界区应变比与滑移传递因子无关,此时晶粒均易于变形,晶界区应变接近平均应变,例如Tilt(100)模型的应变比接近1,如图6b1~b3所示。
平面应变时,晶界区应变比同样与滑移传递因子正相关,如图6c1~c2所示。此外,滑移分切应力因子也显著影响晶界区变形(图6c3),较高的滑移分切应力因子可促进晶界区趋于均匀变形,例如Twist(100)模型拥有较高的滑移分切应力因子(> 0.4),此时滑移传递因子对晶界区应变非均匀性的影响降低,2者之间的关系不再单调。
在晶界区强化方面,剪切时的晶界区流动应力与滑移分切应力直接相关,随着滑移分切应力因子的增大,流动应力近乎单调降低,如图7a所示。由于单轴拉伸时晶粒滑移分切应力因子多大于0.4,因而各模型间的流动应力差异较小(变化范围多在350~550 MPa,图7b),滑移分切应力对流动应力的影响不明显。另一方面,单轴拉伸时晶粒应变差异大,当滑移分切应力因子过低时易出现严重的应变集中,使得采集到的流动应力极低,如图7b所示的Twist(111)模型。平面应变约束时,除发生严重应变集中的模型(如Twist(111)模型)外,流动应力随滑移分切应力因子的提高而单调降低,如图7c所示。
3 结论
(1) 晶间变形协调行为由晶间滑移传递因子和滑移分切应力因子共同决定,2个参数中任意一项占绝对优势时,晶间变形协调即趋于均匀;相反,2者中有一个处于显著低值时即可能导致晶界区的应变集中现象。
(2) 相邻晶粒的滑移传递因子对晶界区变形有着直接影响,晶界区域(< 3 μm)的应变比与滑移传递因子正相关,滑移传递因子越大,晶界区变形越均匀。
(3) 晶粒滑移分切应力因子由晶粒取向和应力状态决定。滑移分切应力因子的大小表征晶粒取向的软硬,软取向晶粒的晶界区变形趋于均匀,与晶界的滑移传递因子无关。
(4) 双晶模型的流动应力与滑移分切应力因子近似线性负相关;晶界区GND密度与该区域变形均匀程度相关,高的局部应变梯度(应变均匀性差)会引发高密度的GND,进而促进区域强化。低的滑移分切应力因子会加剧晶界区非均匀变形,进而导致GND密度提高。
来源--金属学报






 沪公网安备31011202020290号
沪公网安备31011202020290号
