分享:FeMnCoCrNi高熵合金双晶微柱变形机制的分子动力学模拟
1
2
为了揭示高熵合金中晶界对塑性变形机制的影响,利用分子动力学模拟方法研究了具有不同初始取向组合的等主元FeMnCoCrNi高熵合金双晶在单轴拉伸变形中的力学性能与变形系统演化,并揭示了晶界与拉伸方向的位向关系对高熵合金力学行为的影响。结果表明,对研究的所有双晶模型而言,位错优先在晶界处形核并向两侧的晶粒内滑移。在变形过程中,晶界发生了不同程度的宽化和弯曲。当晶界与拉伸方向垂直时,颈缩易于在晶界处发生,这导致双晶的流变应力随外加载荷增大而降低。而当晶界平行于拉伸方向时,在整个塑性变形过程中模型保持1 GPa以上的流变应力。相对于其他双晶而言,[111]与[110]取向组合的双晶流变应力波动幅度最大,同时呈现出最强的加工硬化能力。其中应力的下降归因于大量的位错发生了滑移,而高的硬化能力则是由较多的ε-马氏体、层错以及孪晶形成所致。此外,还对比了FeMnCoCrNi、FeCuCoCrNi和纯Cu 3种材料的变形行为。与Cu相比,FeMnCoCrNi和FeCuCoCrNi高熵合金中的晶格畸变使晶界更加粗糙,这使得外加载荷作用下位错易于形核,且层错能较低的FeMnCoCrNi中形成的ε-马氏体最多。
关键词:
为了满足飞速发展的现代工业和科技的需求,多主元素合金(高熵合金)的设计理念应运而生[1]。高熵合金自问世以来,由于其高强度/硬度[2,3]、优异的断裂韧性[4]、较好的耐磨性与抗腐蚀性[5,6],以及甚至打破了强度与塑性倒置关系等特性[7~9]而引起材料学者的广泛关注。与传统合金相比,高熵合金独特的结构和性能归因于四大效应,即高熵效应、迟滞扩散效应、晶格畸变效应和“鸡尾酒”效应[10,11]。其中晶格畸变效应与高熵合金的宏观力学性能及微观变形机制密切相关[11]。
由3d过渡族金属元素构成的中、高熵合金通常是以fcc结构为主的单相或双相固溶体[12],例如,CoCrNi[13,14]、CoVNi[15]、FeCoCrNi[16]、FeMnCoCr[7,8,17~19]、FeMnCoCrNi[4,20~22]和FeCuCoCrNi[23]等。当这些合金发生塑性变形时,由于多种变形机制协同作用,在强度提升的同时还保持较高的塑性[8,17,24]。目前这类高熵合金在变形过程中的位错滑移、孪生以及相变等微观变形机制已被广泛研究[4,7,8,25]。但多晶材料中广泛存在的面缺陷(即晶界)对此类合金微观变形的影响却鲜有报道。
晶界对材料的力学行为和塑性变形机制具有显著的影响。当晶粒尺寸大于100 nm时,晶界阻碍位错运动,这导致位错在界面处塞积从而起到强化作用。当晶粒尺寸在数十纳米时,晶界对位错滑移的阻碍减弱,变形机制从位错塞积转变为非相关位错滑移,即Orowan-type或Whisker-type机制[26]。随着晶粒尺寸继续降低至10 nm以下时,塑性变形由晶界迁移和晶粒转动主导,这导致反Hall-Petch关系出现[27]。对纳米晶材料而言,晶界占有较高的体积分数。例如,当晶粒尺寸为10 nm时,晶界处的原子数占总原子的14%~27%。在外加载荷作用下晶界可以发射或吸收位错,且晶界的滑移也会释放应力,从而影响材料的力学性能[28]。然而,高熵合金较高的结构熵和晶格畸变导致其晶界的结构和力学行为与传统金属材料存在较大差异[11]。因此,有必要研究纳米晶高熵合金中晶界对宏观力学性能和微观变形机制的影响。
在纳米尺度下,分子动力学模拟可对各种变形系统进行准确、高效地追踪[14,25,29~32]。借助这一模拟方法,Yuasa等[29,30]对Cu/Cu双晶和Co/Cu双晶晶界处的位错发射和晶界滑移行为进行了系统研究,在Co/Cu双晶中,位错由界面处的层错产生。与Cu/Cu双晶相比,Co/Cu双晶中层错的形成并未促进位错发射,且晶界的滑动和迁移行为与自由体积的关系较小。Tan等[31]研究了熵值对FeCuCoCrNi高熵合金中晶界的结构和迁移机制的影响。随着熵值增加,晶界发生粗化,且晶界的迁移机制由集体迁移转变为分散迁移。Lee等[32]模拟了沿<110>和<111>方向单轴拉伸时具有不同对称扭转晶界的FeMnCoCrNi高熵双晶的微观力学行为,结果表明,Schokley不全位错优先在晶界处形核,然后向晶内滑移并留下层错,且位错形核所需的临界剪切应力随着双晶晶界角度的不同而发生变化。
为了揭示晶界对不同取向的高熵合金双晶塑性变形的影响,本工作借助分子动力学方法对具有不同初始取向组合的等原子比FeMnCoCrNi双晶微柱进行了拉伸变形模拟。模拟结果将阐释以下3个问题:(1) 不同取向的高熵双晶如何协调变形;(2) 双晶模型中晶界与变形方向的位向关系(平行或垂直)对材料的宏观性能和微观变形的影响;(3) 具有不同层错能和晶格畸变的高、低熵双晶材料塑性变形机制的差异。以上研究结果将有助于深入理解晶界对高熵合金塑性变形的影响,从而为设计高强韧性的高熵合金材料提供指导。
1 模型与方法
对等主元FeMnCoCrNi高熵合金的拉伸模拟结果表明,[001]和[123]取向单晶微柱的主要变形机制分别为层错的开动和ε-马氏体相变。且与其他取向相比,[110]取向单晶中的孪生行为最为显著,而[111]取向单晶中位错开动的临界应力最大[25]。因此,本工作选取[001]、[110]、[111]和[123] 4种单晶取向进行两两组合来构建双晶模型,即模拟涉及[001] + [110]、[001] + [111]、[001] + [123]、[111] + [110]、[123] + [110]和[111] + [123] 6种取向组合。为了研究晶界与加载方向的位向关系对材料变形的影响,在固定单轴拉伸方向的前提下改变相邻晶粒的相对位置,如图1所示,即分别为拉伸方向与晶界垂直和拉伸方向与晶界平行。图中A和B分别代表具有不同初始取向的单晶,尺寸均为15 nm (X) × 15 nm (Y) × 15 nm (Z)。值得注意的是,改变不同取向晶粒的相对位置后,晶界的粗糙程度虽然存在细微差异,但晶界的宽度均仅为2~3层原子间距,且不同双晶模型在变形前均未发现晶界附近有明显的位错,因此忽略了晶界微观结构的细微差异对大变形量下微观变形机制的影响。
图1
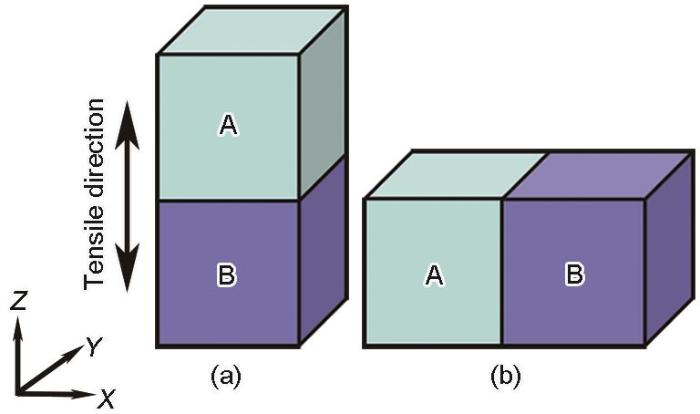
图1 单轴拉伸载荷下的双晶微柱模型示意图
Fig.1 Schematics of the bicrystal micropillar models deformed under uniaxial tension (A and B represent the single crystals with different initial orientations and sizes of 15 nm (X) × 15 nm (Y) × 15 nm (Z))
(a) grain boundary is perpendicular to the deformation direction
(b) grain boundary is parallel to the deformation direction
为研究晶粒尺寸对变形系统演化的影响,选取取向为[110],尺寸分别为5 nm (X) × 5 nm (Y) × 10 nm (Z)和15 nm (X) × 15 nm (Y) × 30 nm (Z)的FeMnCoCrNi单晶进行单轴拉伸变形的模拟对比。
为了揭示层错能和晶格畸变对双晶模型变形机制的影响,选取具有相同几何尺寸和拉伸方向的等原子比FeCuCoCrNi高熵合金和纯Cu进行了对比研究。采用MEAM (modified embedded atom method)势描述FeMnCoCrNi和Cu模型内原子的相互作用[33,34]。对FeCuCoCrNi高熵合金则选取EAM (embedded atom method)势[23],基于此势函数FeCuCoCrNi的平均点阵位移约为0.0027 nm,即晶格畸变程度约为0.7%,与采用第一性原理计算得到的FeMnCoCrNi晶格畸变程度相近[23]。上述势函数被广泛用来描述合金的力学行为和塑性变形机制。经计算,FeMnCoCrNi、FeCuCoCrNi和纯Cu的晶格常数依次为0.3595、0.3552和0.3615 nm,层错能分别为-45、62和41 mJ/m2,这些模拟结果与文献[23,33~35]报道一致。
分子动力学计算采用LAMMPS (large-scale atomic/molecular massively parallel simulator)软件包[36]模拟实现。对所有模型均进行300 K下的单轴拉伸变形模拟,变形方向(Z)为周期性边界条件,其他2个正交方向(X、Y)为自由边界条件。为了获得大塑性变形下不同变形系统的演化及其对力学性能的影响,施加的最大应变(工程应变ε)为100%。变形前,先对模型进行能量最小化处理,然后在300 K下进行模拟退火处理,以消除不合理的原子配置并释放内应力,使Z方向上的压力为0。最后对模型进行单轴拉伸模拟,模拟时间步长为5 fs。选取的应变速率为108 s-1。模拟结果的可视化通过OVITO (open visualization tool)实现[37],不同种类的原子结构和位错类型分别采用CNA (common neighbor analysis)[38]和DXA (dislocation analysis)[39]算法进行分析。
2 结果与讨论
2.1 不同晶粒尺寸单晶的力学行为
[110]取向下2种晶粒尺寸单晶的应力-应变曲线以及相应不同变形系统体积分数的演化如图2所示。在整个变形过程中,2个模型的应力-应变曲线形状相似(图2a和c),即晶粒尺寸对力学行为无明显影响。在塑性变形初期(5% < ε < 30%),2个模型中层错、孪晶和ε-马氏体体积分数随应变的增加而增加(图2b和d),且均贡献于加工硬化(图2a和c)。随加载的继续,2个模型中ε-马氏体的体积分数均降低(图2b和d)。模拟结果表明,纳米尺度下,晶粒尺寸对FeMnCoCrNi高熵合金微观变形机制无显著影响。
图2

图2 [110]取向下不同晶粒尺寸FeMnCoCrNi单晶的应力-应变曲线和相应不同形变系统的体积分数随应变的演化
Fig.2 Stress-strain curves (a, c) and corresponding volume fraction evolutions (b, d) of the [110]-oriented FeMnCoCrNi single crystals with domain sizes of 5 nm (X) × 5 nm (Y) × 10 nm (Z) (a, b) and 15 nm (X) × 15 nm (Y) × 30 nm (Z) (c, d) (SF—stacking fault, TB—twin boundary)
2.2 晶界垂直于拉伸方向时双晶模型的力学行为
当晶界垂直于拉伸变形方向时,不同FeMnCoCrNi双晶模型的应力-应变曲线和弹塑性转变点处的应力分别如图3和表1所示。在弹性变形阶段,随着应变增加,各模型的应力均近似呈线性增大直至达到弹塑性转变点。之后,应力便呈现出不同程度的下降,模型进入塑性变形阶段(图3)。在弹塑性转变点处,各模型的应力从大到小依次为[001] + [111]、[111] + [123]、[001] + [123]、[123] + [110]、[001] + [110]和[111] + [110]双晶。此时,双晶模型的应力均小于其组成单晶的应力(表1)。在塑性变形阶段,随着载荷增大,除[001] + [111]模型外,其余各模型呈现出不同程度的加工硬化,如图3中阴影区域所示,这归因于模型内形成了层错、孪晶和ε-马氏体等多种变形系统。由于[001] + [111]模型中较早发生了颈缩,因此其应力随应变的增加呈逐渐下降的趋势。当工程应变达到45%后,各模型的应力均随应变的增加而快速下降,直至断裂。值得注意的是,在应变为2%~5%时,[111] + [110]模型的应力呈现急剧下降的趋势,随后在应变为5%~20%时呈现出最为显著的加工硬化(图3)。
图3
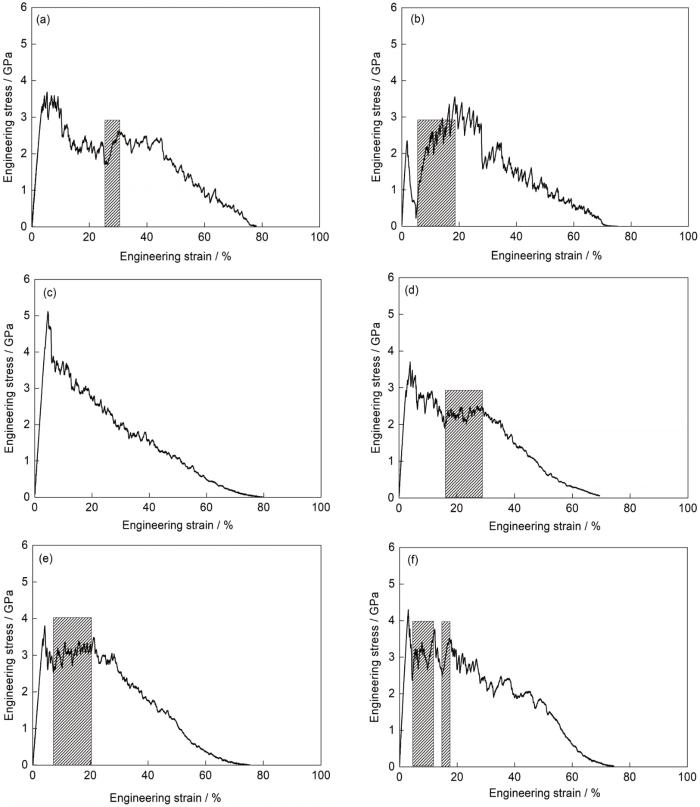
图3 晶界与拉伸方向垂直时不同取向组合双晶的应力-应变曲线
Fig.3 Stress-strain curves of the bicrystals with different orientation combinations when the grain boundary is perpendicular to the tensile direction (The shaded areas indicating work hardening)
(a) [001] + [110] (b) [111] + [110]
(c) [001] + [111] (d) [123] + [110]
(e) [001] + [123] (f) [111] + [123]
表1 晶界与拉伸方向垂直时单晶与双晶在弹塑性转变点处的应力
Table 1
| Crystal type | Orientation | Stress / GPa |
|---|---|---|
| Single crystal | [001] | 5.13 |
| [110] | 4.11 | |
| [111] | 7.43 | |
| [123] | 4.43 | |
| Bicrystal | [001] + [110] | 3.59 |
| [001] + [111] | 5.12 | |
| [001] + [123] | 3.80 | |
| [111] + [110] | 2.33 | |
| [123] + [110] | 3.70 | |
| [111] + [123] | 4.30 |
为了揭示单轴拉伸过程中微观变形系统的演化,各模型在弹塑性转变点处的原子结构和位错线分布分别如图4a~f和a1~f1所示。在所有模型中,Schockley不全位错优先在晶界处形核并随着变形量增大向晶粒内部滑移,且位错滑移后形成层错。由于晶体结构的差异,不同相之间的界面处通常存在失配位错结构[29]。由于FeMnCoCrNi双晶晶界两侧晶粒的取向不同,因此晶界处存在失配应变,进而导致位错在外加载荷作用下更易形核并向晶内滑移,即晶界处位错的形核由失配应变和变形共同导致。位错的滑移面和滑移方向与由Schmidt定律计算得到的优先开动的滑移系统一致。在[001] + [110]、[001] + [111]、[001] + [123]和[123] + [110]双晶模型中仅有少量位错在自由表面处形核(图4a1、b1、c1和e1)。对单晶模型的模拟结果表明,位错优先在自由表面形核[25,33]。与单晶相比,双晶模型中位错形核的临界应力较小,即晶界处更易促进位错形核。弹塑性转变点处[001] + [110]、[001] + [111]、[001] + [123]、[111] + [110]、[123] + [110]和[111] + [123]双晶的位错密度分别为1.003 × 1016、3.132 × 1016、0.975 × 1016、8.722 × 1016、0.997 × 1016和5.239 × 1016 m-2。与其他模型相比,[111] + [110]模型晶界处的位错密度最高。随着载荷增加,此模型中被激发出大量的位错且位错滑移方向指向[111]晶粒(图4d1)。这导致材料的应力迅速下降(图3)。当应变增加至约20%时,[111]和[110]晶粒内形成的层错、ε-马氏体和孪晶(图5)共同导致此双晶模型呈现较为显著的加工硬化。
图4

图4 晶界与拉伸方向垂直时不同取向组合的FeMnCoCrNi双晶在弹塑性转变点处的原子结构和位错线分布
Fig.4 Atomic structures (a-f) and corresponding dislocation line distributions (a1-f1) for the FeMnCoCrNi bicrystals with different orientation combinations at elastic-to-plastic transition point when the grain boundary is perpendicular to the tensile direction (a, a1) [001] + [110], engineering strain ε = 4.4% (b, b1) [001] + [111], ε = 4.6% (c, c1) [001] + [123], ε = 4.2% (d, d1) [111] + [110], ε = 1.9% (e, e1) [123] + [110], ε = 3.9% (f, f1) [111] + [123], ε = 3.0%
图5
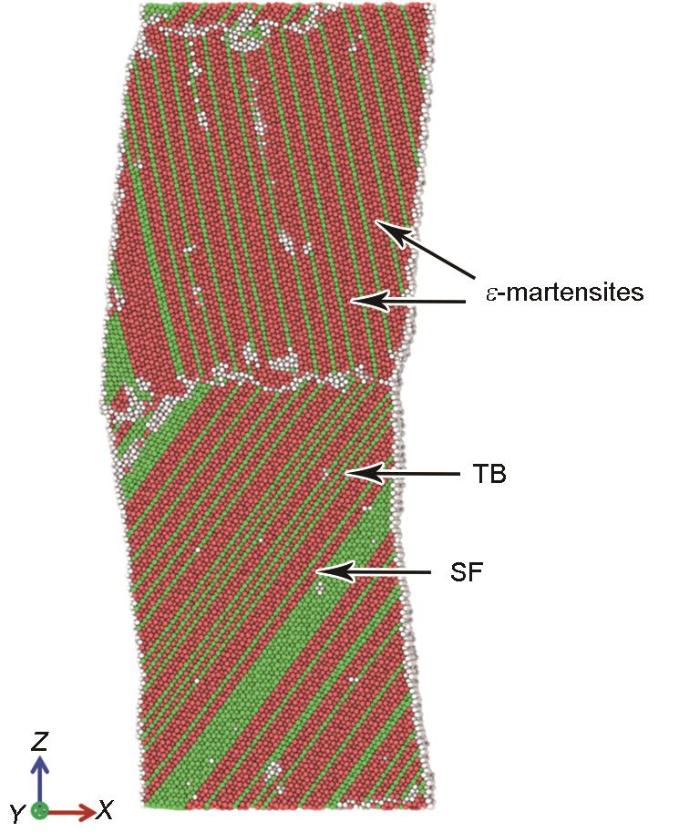
图5 应变为20%时[111] + [110]双晶模型的原子结构
Fig.5 Atomic structure for the [111] + [110] bicrystal at ε = 20%
当外加应变达到45%时,各模型的原子结构和位错线分布分别如图6a~f和a1~f1所示。所有模型均呈现出不同程度的颈缩,同时晶粒内部的变形不均匀。此外,晶界还呈现出宽化和弯曲的特征。除[001] + [111]和[111] + [110]双晶模型的颈缩发生在非晶界处外,其余模型的颈缩均在晶界发生,且颈缩位置的部分原子呈现非晶态,这表明当晶界与变形方向垂直时,颈缩更倾向于在晶界发生。双晶模型中各晶粒变形系统的开动与相同取向单晶的模拟结果[25]一致。其中,与[001]取向的晶粒相比,[110]、[111]和[123]取向的晶粒中开动了较多的ε-马氏体,且在这4种不同取向的晶粒中[110]晶粒内的位错密度最低。在[111] + [110]模型中,[111]晶粒内的位错密度与其他双晶模型中该取向晶粒相比较低(图6d1),这归因于[111]取向的晶粒内开动了较多的层错和ε-马氏体(图6d)。由此可见,[111] + [110]双晶模型中的晶界促进了[111]晶粒中层错和马氏体相变的发生,进而抑制了位错滑移。
图6

图6 晶界与拉伸方向垂直时不同取向组合的FeMnCoCrNi双晶在45%工程应变时的原子结构和位错线分布
Fig.6 Atomic structures (a-f) and corresponding dislocation line distributions (a1-f1) for the FeMnCoCrNi bicrystals with different orientation combinations at ε = 45% when the grain boundary is perpendicular to the tensile direction (a, a1) [001] + [110] (b, b1) [001] + [111] (c, c1) [001] + [123] (d, d1) [111] + [110] (e, e1) [123] + [110] (f, f1) [111] + [123]
2.3 晶界平行于拉伸方向时双晶模型的力学行为
当双晶模型的晶界与变形方向平行时,单轴拉伸载荷下各模型的应力-应变曲线和弹塑性转变点处的应力分别如图7和表2所示。在弹性变形阶段,模型的应力随应变的增加呈线性上升的趋势(图7)。当应力达到弹塑性转变点时,各模型的应力按由高到低排列依次为[001] + [111]、[111] + [123]、[111] + [110]、[001] + [123]、[123] + [110]和[001] + [110] (表2)。进入塑性变形阶段后,随着应变增加,由于[111] + [110]模型中形成了大量的ε-马氏体,因此呈现出最为显著的加工硬化,这将在下文详细描述。其次为[123] + [110]和[001] + [110]模型,如图7中阴影区域所示,其他模型的应力随变形增加总体呈现下降的趋势。当应变达到100%时,所有模型的应力仍保持在1 GPa以上。与晶界垂直于应力轴的模拟相比,晶界平行于变形方向时模型在弹塑性转变点处的应力水平略高,且在塑性变形阶段的流变应力随变形的演化更加平稳,这归因于模拟中晶界的位向和模型几何形状的差异。
图7
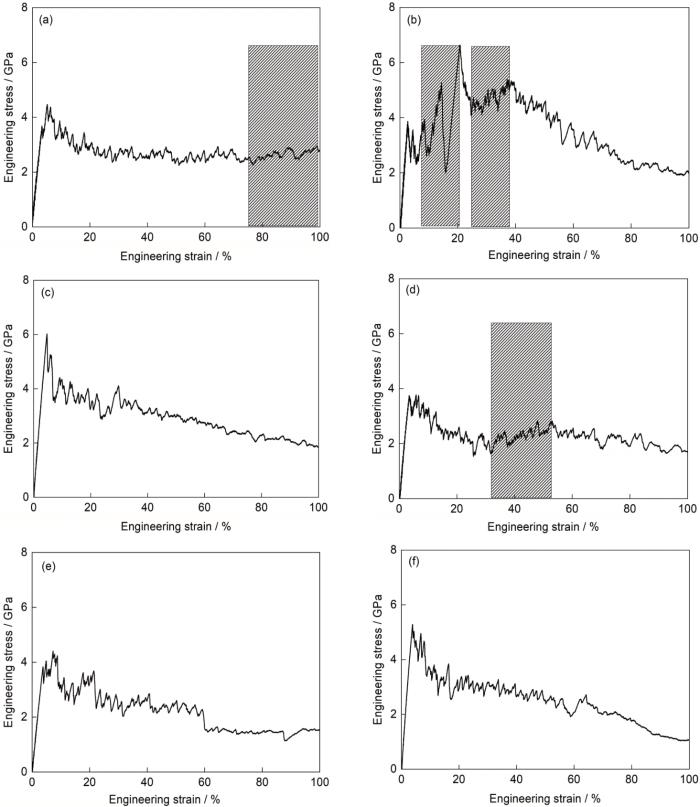
图7 当晶界与拉伸方向平行时不同取向组合双晶的应力-应变曲线
Fig.7 Stress-strain curves of the bicrystals with different orientation combinations when the grain boundary is parallel to the tensile direction (The shaded areas indicating work hardening)
(a) [001] + [110] (b) [111] + [110]
(c) [001] + [111] (d) [123] + [110]
(e) [001] + [123] (f) [111] + [123]
表2 当晶界与拉伸方向平行时单晶与双晶在弹塑性转变点处的应力
Table 2
| Crystal type | Orientation | Stress / GPa |
|---|---|---|
| Single crystal | [001] | 5.13 |
| [110] | 4.11 | |
| [111] | 7.43 | |
| [123] | 4.43 | |
| Bicrystal | [001] + [110] | 3.62 |
| [001] + [111] | 6.03 | |
| [001] + [123] | 3.83 | |
| [111] + [110] | 3.87 | |
| [123] + [110] | 3.72 | |
| [111] + [123] | 5.28 |
当外加载荷达到弹塑性转变点时,位错开始形核,如图8所示,此时,晶界仍为位错优先形核的位置(图8a1~f1),此外,在[001] + [110]、[001] + [111]、[001] + [123]和[111] + [123]双晶模型中也可观察到少量位错在自由表面处形核(图8a1~c1、f1)。与晶界垂直于拉伸方向的情形(图4)相似,位错滑移后会在晶粒内留下层错。在双晶模型中,位错优先向易于开动位错的晶粒内部滑移(图8a~f)。
图8
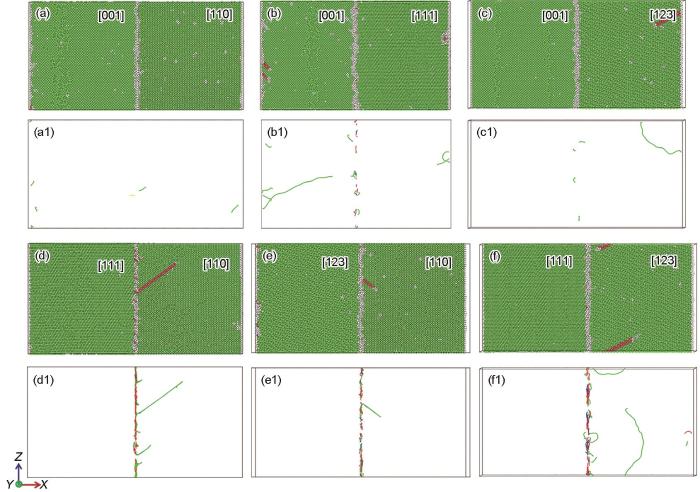
图8 晶界与拉伸方向平行时不同取向组合的FeMnCoCrNi双晶在弹塑性转变点处的原子结构和位错线分布
Fig.8 Atomic structures (a-f) and corresponding dislocation line distributions (a1-f1) for the FeMnCoCrNi bicrystals with different orientation combinations at elastic-to-plastic transition point when the grain boundary is parallel to the tensile direction
(a, a1) [001] + [110], ε = 3.3% (b, b1) [001] + [111], ε = 4.6% (c, c1) [001] + [123], ε = 3.8%
(d, d1) [111] + [110], ε = 2.7% (e, e1) [123] + [110], ε = 3.5% (f, f1) [111] + [123], ε = 3.9%
当变形结束后,各双晶模型均发生了非均匀塑性变形,如图9a~f所示。在[001] + [110]、[001] + [111]、[001] + [123]、[111] + [110]和[123] + [110]模型中晶界发生了显著的宽化和非晶化,同时还伴随着晶界的弯曲(图9a~e)。而在[111] + [123]模型中则主要发生了晶界弯曲(图9f)。各双晶模型中的变形机制均以层错和ε-马氏体相变为主,且不同取向晶粒内的位错分布规律(图9a1~f1)与同一取向单晶的模拟结果[25]一致。此外,与晶界垂直于变形方向的结果相比,此时各模型的整体形状变化较为均匀。
图9

图9 晶界与拉伸方向平行时不同取向组合的FeMnCoCrNi双晶在100%工程应变时的原子结构和位错线分布
Fig.9 Atomic structures (a-f) and corresponding dislocation line distributions (a1-f1) for the FeMnCoCrNi bicrystals with different orientation combinations at ε = 100% when the grain boundary is parallel to the tensile direction (a, a1) [001] + [110] (b, b1) [001] + [111] (c, c1) [001] + [123] (d, d1) [111] + [110] (e, e1) [123] + [110] (f, f1) [111] + [123]
综上所述,当晶界与变形方向的位向关系不同时,虽然在弹塑性转变点处,位错均更易在晶界处形核,但在塑性变形过程中晶界对双晶模型的力学行为和塑性变形机制的影响存在显著差异。具体而言,当晶界垂直于变形方向时,在拉应力作用下,晶界处更易积累缺陷,从而发生颈缩,导致双晶模型的应力下降。而当晶界平行于变形方向时,拉应力与晶界平行,垂直于晶界方向的受力较小,在变形过程中材料出现了晶界宽化和弯曲,进而协调了双晶体的塑性变形。这表明通过调控合金中晶粒的取向和晶界与变形方向的位向关系可提升材料的塑性变形能力。
2.4 层错能和晶格畸变对双晶变形机制的影响
对fcc结构金属而言,层错能决定了变形过程中不同变形系统的开动[21,40,41]。除此之外,高熵合金中显著的晶格畸变亦对其宏观力学性能和微观变形系统演化有重要影响[42]。为了揭示层错能和晶格畸变对高熵双晶模型微观力学行为和塑性变形机制的影响,选取等主元的FeMnCoCrNi、FeCuCoCrNi 2种高熵合金与纯Cu进行对比研究。FeMnCoCrNi和FeCuCoCrNi合金的晶格畸变相近,层错能是导致2种材料变形机制存在差异的主要原因。而FeCuCoCrNi和Cu的层错能相近,则晶格畸变是导致2者微观力学行为不同的主要因素。
如表1所示,取向为[111]和[110]的2个单晶相比,位错开动所需的临界应力相差最大,而[123]和[110]取向单晶位错开动的临界应力最为接近,且与其他双晶模型相比,[111] + [110]模型的力学行为差异较大(图3和7)。因此,为了简化研究晶界对3种金属材料力学行为的影响,选取[111] + [110]和[123] + [110] 2种取向组合的双晶进行单轴拉伸变形模拟。
变形前,3种材料不同双晶模型界面处的原子结构和原子势能分布如图10所示。当晶界与变形方向垂直时,FeMnCoCrNi和FeCuCoCrNi 2种双晶模型的晶界与Cu相比较为粗糙,同时,FeMnCoCrNi的晶界比FeCuCoCrNi的粗糙。此外,与[123] + [110]双晶模型相比,3种金属的[111] + [110]模型中晶界处的原子结构较为平直和光滑(图10a)。晶界处的原子势能分布表明不同材料双晶模型的晶界能存在差异。如图10b所示,与FeMnCoCrNi和FeCuCoCrNi高熵合金相比,Cu中晶界处的原子势能较高,且晶界的原子结构对原子势能无显著影响。当晶界与变形方向平行时,不同双晶模型晶界处的原子结构(图10c)粗糙程度的差异减小,而原子势能分布(图10d)的规律与晶界垂直于变形方向时一致。这表明,金属材料内晶界的原子结构不仅与熵值有关,还受元素种类及晶界两侧晶体取向的影响,而原子势能的分布主要取决于元素种类。
图10
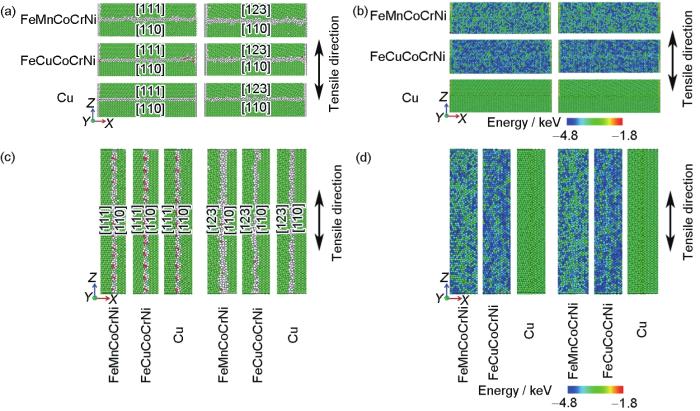
图10 FeMnCoCrNi、FeCuCoCrNi和Cu双晶晶界处的原子结构和原子势能分布
Fig.10 Atomic structures (a, c) and distributions of atomic potential energy (b, d) at grain boundaries for FeMnCoCrNi, FeMnCoCrNi, and pure Cu bicrystals when the grain boundary is perpendicular (a, b) and parallel (c, d) to the tensile direction
当晶界与拉伸方向垂直时,FeMnCoCrNi、FeCuCoCrNi和Cu 3种金属的[111] + [110]和[123] + [110]双晶模型的应力-应变曲线如图11a1~a3所示。工程应变为5%和20%时[111] + [110]和[123] + [110]双晶模型的原子结构分别如图11b1~b3和c1~c3所示。在同一取向组合下,Cu在弹塑性转变点处的应力最大,其次为FeCuCoCrNi和FeMnCoCrNi合金。这归因于高熵合金中较大的晶格畸变,且与FeCuCoCrNi (非稳定层错能为278 mJ/m2)和Cu (非稳定层错能为305 mJ/m2)相比,FeMnCoCrNi的非稳定层错能(222 mJ/m2)最小所致。当取向组合为[111] + [110]时,由于晶格畸变导致位错易于在高熵合金的晶界处形核且大量位错向[111]晶粒内滑移(图4d1),因此,与[123] + [110]取向组合相比,[111] + [110]取向组合FeMnCoCrNi和FeCuCoCrNi合金在弹塑性转变点处的应力较小。对于纯Cu而言,由于无晶格畸变,位错仅在晶界处被激发并向晶界两侧滑移,因此2种取向组合的模型中位错开动的临界应力相近。
图11

图11 晶界与拉伸方向垂直时FeMnCoCrNi、FeCuCoCrNi和Cu双晶的应力-应变曲线及原子结构
Fig.11 Stress-strain curves (a1-a3), atomic structures of the [111] + [110] (b1-b3) and [123] + [110] (c1-c3) bicrystals when ε = 5% and ε = 20% of FeMnCoCrNi (a1-c1), FeCuCoCrNi (a2-c2), and Cu (a3-c3) bicrystals when the grain boundary is perpendicular to the tensile direction
在塑性变形阶段,选取2个特征载荷点进行变形机制的细致分析。当工程应变为5%时,对于[111] + [110]取向组合的双晶而言,3种材料的应力均呈现显著下降的趋势。在FeMnCoCrNi (层错能为-45 mJ/m2)和FeCuCoCrNi (层错能为62 mJ/m2)的[111]晶粒中形成了大量ε-马氏体和层错,而在[110]晶粒中则主要为层错。在纯Cu (层错能为41 mJ/m2)双晶中则仅形成了层错。当双晶模型的取向组合为[123] + [110]时,3种金属的应力同样出现了不同程度地下降。在FeMnCoCrNi的[123]和[110]晶粒中均开动了层错,而在FeCuCoCrNi和Cu中仅在[110]晶粒中识别到层错。当外加应变增加至20%时,相对于其他模型而言,FeMnCoCrNi和FeCuCoCrNi的[111] + [110]模型呈现显著的加工硬化,这对应于这2个模型中较多的ε-马氏体、层错以及少量孪晶的形成。当模型取向组合为[123] + [110]时,在FeCuCoCrNi和Cu双晶的晶界处均发生了断裂,这是由Cu原子较高的势能引起的纯Cu及含Cu合金晶界的能量升高(图10b和d)且[123] + [110]双晶模型中晶界处的原子排列粗糙(图10a)所致。
当晶界与拉伸方向平行时,与图11的结果相似,3种材料不同双晶模型的应力-应变曲线以及特征载荷处的原子结构如图12所示。在同一取向组合下,虽然FeCuCoCrNi和Cu的晶格畸变不同,但2者的非稳定层错能相近。在弹塑性转变点处FeCuCoCrNi和Cu的应力相近且高于FeMnCoCrNi。这表明,对不同金属而言,当晶界平行于变形方向时,位错开动所需的临界应力主要取决于非稳定层错能。而对于同种金属,不同取向组合的模型中位错开动的临界应力相近。在塑性变形阶段,与[123] + [110]相比,3种金属[111] + [110]双晶模型的流变应力较高,同时伴随有较明显的应力波动。而当取向为[111] + [110]时,与FeCuCoCrNi和Cu相比,在50%应变后FeMnCoCrNi的应力下降显著。
图12

图12 晶界与拉伸方向平行时FeMnCoCrNi、FeCuCoCrNi和Cu双晶的应力-应变曲线及原子结构
Fig.12 Stress-strain curves (a1-a3), atomic structures of the [111] + [110] (b1-b3) and [123] + [110] (c1-c3) bicrystals when ε = 5%, ε = 20%, and ε = 100% of FeMnCoCrNi (a1-c1), FeCuCoCrNi (a2-c2), and Cu (a3-c3) bicrystals when the grain boundary is parallel to the tensile direction
进入塑性变形后,当工程应变为5%时,在3种金属不同取向组合的双晶模型中位错滑移后形成的层错为主要变形系统。当继续加载至20%应变时,在[111] + [110]取向组合的FeMnCoCrNi双晶中,以及此取向下FeCuCoCrNi和Cu的[110]晶粒中发生了显著的ε-马氏体相变,这导致宏观应力的增大。而在[123] + [110]模型中,3种金属的主要变形系统均为层错,因此未导致应力随变形增加显著提升。当应变为100%时,在取向组合为[111] + [110]的FeMnCoCrNi中发生了颈缩,晶界严重弯曲,部分原子出现了非晶化,同时还伴随有部分区域发生了逆相变。颈缩导致FeMnCoCrNi在变形后期的应力下降。而在FeCuCoCrNi的[110]晶粒和Cu的[111]、[110]晶粒中,逆相变行为更加显著且变形更加均匀,因此双晶模型整体的流变应力较高。当模型取向组合为[123] + [110]时,由于FeMnCoCrNi的层错能较低,因此合金中开动了多种变形系统。在FeCuCoCrNi的[123]和[110]晶粒中以及Cu的[110]晶粒中发生了层错的消退。3种金属均发生非均匀塑性变形,因此变形结束后的应力呈现略微下降的趋势。通过将FeMnCoCrNi、FeCuCoCrNi和纯Cu 3种材料双晶模型的变形进行对比,发现在相同取向关系和拉伸方向下,较传统低熵材料而言,高熵合金中较大的晶格畸变使晶界更加粗糙,这使得在一定外加载荷作用下,位错易于在高熵合金中形核,且层错能亦对高熵合金的位错行为和马氏体相变有重要影响。
综上所述,本工作系统研究了纳米尺度下不同初始取向组合的高熵双晶在单轴拉伸载荷下力学性能及微观变形机制的异同,同时还通过与低熵金属材料对比,揭示了金属的本征属性(如层错能和晶格畸变)对高熵合金双晶微观力学行为的影响,该工作丰富了高熵合金的塑性变形理论,并可为微纳米尺度多晶金属材料的微结构和取向设计提供理论指导。
3 结论
(1) 对FeMnCoCrNi高熵合金双晶模型而言,在弹塑性转变点处,位错优先在晶界处形核并向两侧的晶粒内滑移。在塑性变形过程中,晶界发生了不同程度的宽化和弯曲,双晶模型中各晶粒的变形系统开动与相同取向单晶的模拟结果一致。当晶界与变形方向垂直时,颈缩易于在晶界处发生,这导致模型整体的流变应力下降。而当晶界与变形方向平行时,模型在整个塑性变形过程中保持1 GPa以上的流变应力。
(2) 在FeMnCoCrNi高熵合金的双晶模型中,[111]与[110]取向组合的双晶流变应力波动幅度最大,同时呈现出最强的加工硬化能力。其中,应力的下降归因于大量的位错发生了滑移,而硬化则是由较多的ε-马氏体、层错以及孪晶形成所致。
(3) 当晶界与变形方向垂直时,与Cu相比,FeMnCoCrNi和FeCuCoCrNi高熵合金中的晶格畸变使晶界更加粗糙,这使得在相同载荷条件下高熵合金中的位错易于形核,且层错能较低的FeMnCoCrNi中形成的ε-马氏体最多。由于Cu原子的势能较高,晶界的稳定性降低,从而导致FeCuCoCrNi和Cu在晶界位置发生了断裂。当晶界与变形方向平行时,3种金属弹塑性转变点处的应力主要取决于非稳定层错能的大小。
来源--金属学报






 沪公网安备31011202020290号
沪公网安备31011202020290号
