分享：辐照条件下Fe-Cu合金中富Cu析出相的临界形核尺寸和最小能量路径的弦方法计算

刘续希1, 柳文波,1, 李博岩2, 贺新福3, 杨朝曦1, 恽迪1

反应堆压力容器(reactor pressure vessel,RPV)是支撑反应堆内的所有构件、装载反应堆堆芯、容纳一回路冷却剂并维持其压力的承压壳体,是核电站寿命设计中不可拆换的核心部件[1]。RPV钢通常采用具有辐照稳定性和长期可靠性等特点的铁素体合金钢[2]。长期处于高温高压(290℃、16 MPa)服役环境下,RPV钢会出现辐照硬化和辐照脆化等性能退化现象[3,4],严重影响反应堆安全。研究[5,6]发现,RPV钢在中子辐照下产生的高密度、小尺寸(约2 nm)的富Cu析出相具有阻碍位错运动的作用,是造成辐照脆化和辐照硬化的主要原因。然而,实验研究[7,8]发现,RPV钢在0.026和0.051 dpa的中子辐照后,传统透射电镜下没有观察到富Cu析出相,但同样出现了辐照硬化现象。这一现象的产生,极有可能是辐照硬化初期尺寸极小、难以通过传统实验器材观察到的富Cu析出相所造成的。此外,辐照环境下Cu元素析出速率会极大地提升,这与辐照导致点缺陷大量增加密切相关[6]。因此,通过理论模拟研究辐照硬化初期Fe-Cu合金中细小富Cu相的析出行为具有重要意义。

近年来,相场方法在模拟核材料的组织演变方面展现了巨大的潜力[9],国内外学者针对RPV钢的第二相析出行为也进行了一些模拟[10~13]。相场方法基于Ginzburg-Landau理论和连续界面假设,不仅能高效地展现RPV钢富Cu相析出过程的微观组织变化,而且能动态显示析出过程的浓度场变化情况。Molnar等[14]提出了Fe-Cu合金中富Cu相析出的多尺度模拟,并提出了较为泛用的相场模型模拟手段。最近,Zhu等[15]利用相场理论研究了Fe-Cu合金的富Cu析出相从bcc结构向9R结构的转变过程,从晶体学转变的角度考虑了相变过程中的弹性能。赵宝军等[16]利用相场方法研究了Mn含量对Fe-Cu-Mn合金纳米富Cu析出相的影响。Yan等[17]在利用相场研究Fe-Cr合金的两相分离时提出了一种新的包含缺陷浓度的自由能表达形式。然而,相关研究并未系统考虑Fe-Cu合金中富Cu相析出的形核行为,也没有考虑Fe-Cu合金析出行为受辐照条件的影响。前者可能是影响其低剂量辐照下辐照硬化机制的重要因素,后者则是含Cu铁合金工作环境下的必然因素。

基于能量路径(energy path)优化的约束条件弦方法(constrained string method)是研究析出相的临界形核尺寸和最优能量路径的重要方法[18~20]。作为遗传算法的一种分支,弦方法以弦变量作为演化对象。将弦方法用于析出相形核初期的计算,不仅可以体现形核过程中浓度场的动态演变,而且能够再现临界形核过程和最优能量路径的匹配特性。最近,Li等[18,21,22]利用相场模型和约束条件弦方法结合的物理模型对Fe-Cu及Fe-Cu-Mn合金热力学环境下的析出情况进行了模拟,并计算得到了Cu元素的热力学条件下临界形核尺寸及形核能量路径。Zhang等[23,24]较为全面地介绍了相场模型结合约束条件弦方法的计算手段,并在此基础上对二元固体材料相析出过程和临界形核半径进行了模拟计算。以上工作对Fe-Cu合金在辐照条件下的小尺寸富Cu相析出行为的研究提供了可行思路。

本工作基于相场模型和约束弦方法,构建了Fe-Cu合金在辐照条件下的富Cu相析出过程的相场模型,并结合弦方法,使用半隐式Fourier方程[25]对辐照条件下富Cu相形核析出过程的浓度场进行计算,得到了临界形核尺寸和最优能量路径。分别研究了温度、Cu含量、辐照强度3个因素对RPV模型钢Fe-Cu合金中的小尺寸富Cu相的析出行为的影响,计算得到了不同条件下的临界形核半径、形核能量路径、空位形成与分布,并对计算结果进行了定性分析。

1 模型建立

1.1 弦方法简介

图1所示为第二相析出过程的形核阶段的能量路径变化示意图。图1a中的曲面为在形核过程中形核能的所有可能变化路径形成的曲面示意图,图中的3条曲线为形核过程中形核能随着时间演化的3条能量路径。图1b为图1a中的3条能量路径所对应的能量势垒的示意图。State 1与State 2为形核开始与结束时所对应的稳定状态。图中的黄色能量路径(EP i )为第i次演化的能量路径,用“弦”表示其形核浓度场的变化情况。假设该能量路径及其“弦”上一共有N个状态点,每个状态点用L(i, n)表示(i = 1、2、…、I,其中I为总演化次数；n = 1、2、…、N)。L(i, n)用来描述第i次演化对应的形核过程中第n个状态下的浓度场分布[18,19]。如图1a所示,黄色能量路径所对应“弦”经过演化之后产生的新“弦”为蓝色能量路径所对应的“弦”。蓝色能量路径记为EP i + 1,其“弦”上状态用L(i + 1, n)表示。在演化过程中,黄色“弦”上的每个点均向能量更低的方向移动dL,最后经插值得到蓝色“弦”。由于每个点都是朝着能量更低的方向靠近,因此演化后的“弦”将朝能量更低的方向靠近,“弦”的最高点也逐步降低[19]。经过I轮演化,最终可以获得满足约束条件的最小能量路径,即图中的红色“弦”。红色“弦”的最高点将是所有“弦”各自最高点的最低值,也是整个曲面的“鞍点”。

图1

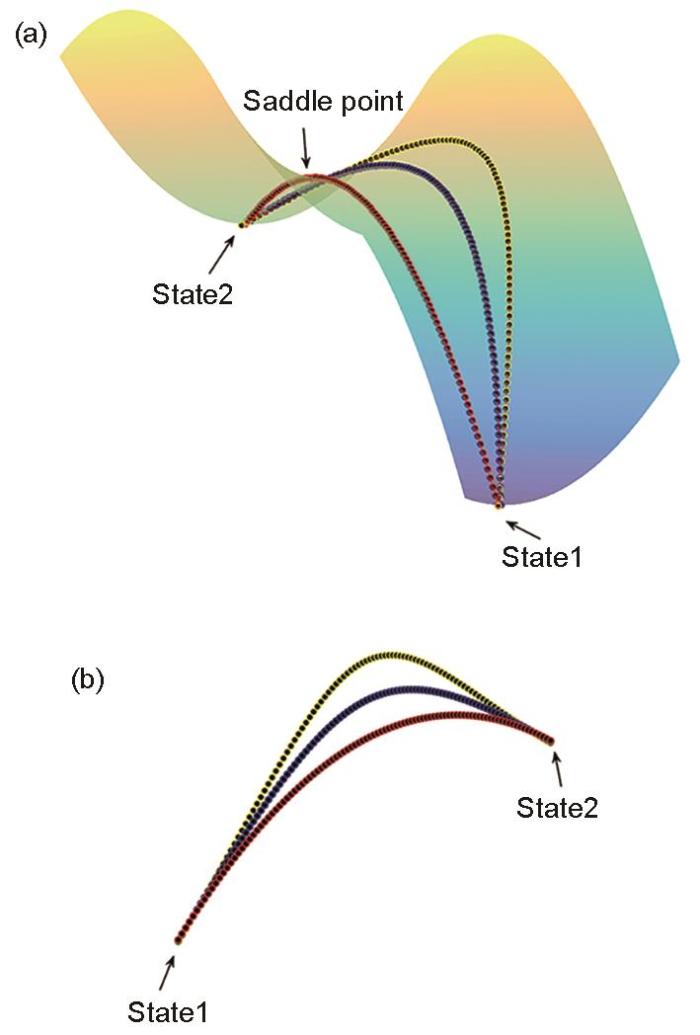
图1   形核过程鞍点示意图

Fig.1   Schematics of saddle points in the nucleus evolutionary correction process

(a) energy path saddle point diagram(b) energy path height contrast diagram

约束条件弦方法首先需确定所研究目标的约束条件[18~20]。由于空位的浓度非常低,本工作假设在Fe-Cu合金中,Fe元素与Cu元素的含量总和守恒(本工作的约束条件)：

式中,CCu0为初始设定的Cu元素浓度,CFe为Fe元素浓度,r为空间坐标,ρ为所研究材料的原子密度。

第i轮演化中,非最低能量路径的弦在弦状态L(i, n)的演化表达式为[20]：

式中,E为能量函数,τ为当前能量路径的切向单位向量,dL为能量路径的移动微元。

为保证弦的移动收敛,弦方法中需要增加2个限制：(1) 需要对每轮修正后的插值进行替换,保证能量路径上每个点的相对距离保持不变,以获得圆滑的能量路径曲线；(2) 维持形核过程能量路径的开始点L(i, 0)和结束点L(i, N)保持不变。事实上,由于形核过程形核能降低的趋势,不会产生能量路径的过分偏离,因此一般只需要固定初始态即可满足上述第2个要求[19,20]。

1.2 相场自由能方程

基于相场理论,含空位的Fe-Cu二元体系的总能量为[17,26~28]：

式中,CCu为Cu元素浓度；CV为空位浓度；T为温度；κCu和κV分别为Cu和空位的界面能梯度系数[17]；NA = 6.022 × 1023,为Avogadro常数；Vm = 7.09 × 10-6 m3/mol,为bcc结构铁素体合金的摩尔体积；G(CCu, CV, T)为体系的Gibbs自由能密度函数；dV为空间微元；Eelas为对应浓度下的弹性能,表示为[28,29]：

式中,εCu和εV分别为Cu和空位的本征应变系数；t为时间,t = nΔt,Δt为数值离散格式的时间步长。

Gibbs自由能密度函数如下[20,23,28]：

式中,Gbulk为各成分的体积能；Gmix为Fe、Cu原子混合过程中的混合自由能；Gnonl为非线性拟合部分；EFe、ECu和EV分别为Fe、Cu和空位的形成能；L为Fe和Cu混杂系数；GFe和GCu分别为bcc结构纯Fe与纯Cu的自由能密度函数的多项式拟合表达式[28],其对应的拟合参数αj 、β、γ的参数取值列于表1[18,28,30]中。弹性能与界面能的相关系数表2[28,29]中。

表1   Fe-Cu合金Gibbs自由能参数[18,28,30]

Table 1  Gibbs free energy parameters of Fe-Cu alloy[18,28,30]

新窗口打开| 下载CSV

表2   Fe-Cu合金的界面能参数与本征应变系数[28,29]

Table 2  Interfacial energy correlation coefficients and eigenstrain coefficients of Fe-Cu alloy[28,29]

新窗口打开| 下载CSV

1.3 辐照下相场方程的演变

相场理论中浓度场变量的演变方程(Cahn-Hilliard方程)为：

式中,Ci 为所关注对象在i轮演化下的浓度场参数,M为迁移率：

式中,D为扩散系数,气体常量R = 8.314 J/(mol·K)。Cu元素和空位缺陷的扩散系数DCu和DV均可由迁移能[31]得到：

式中, ${?}_{\mathrm{m}?″}$为相应成分的迁移能[32]；S为空位浓度降低因数,可表示为：

式中,St为陷阱强度[33]；Am = 0.287 nm,为bcc结构铁合金的晶格常数。辐照条件下产生大量的空位,更多的空位将导致材料边界对空位的吸收速率进一步提升[34]。

不同温度下Fe与Cu的扩散系数和迁移率取值列于表3[29,35]中。

表3   不同温度下扩散系数及迁移率的取值[29,35]

Table 3  Values of diffusion coefficients and mobility at different temperatures[29,35]

新窗口打开| 下载CSV

在考虑空位的产生、复合、吸收等作用后,Cu原子和空位浓度的演化方程为[17]：

式中,PV、RV和SV分别为热力学平衡条件下空位原子的产生速率、空位与间隙原子的复合速率、空位被晶粒边界吸收速率。PV = fr / δV,其中fr为空位生成速率；δV为空位生成速率的校正因子,本工作中δV= 6[17,20]。RV为[17,35]：

式中,V为基体中空位的体积。

辐照时将产生大量的点缺陷,从而影响Cu原子的迁移率。研究[35]表明,在较低辐照温度和低空位浓度下,空间迁移率与整体空位浓度成线性相关关系。因此,辐照条件下迁移率MR及扩散系数DR将表示为：

式中,M0为无辐照条件下的迁移率；CVr为辐照额外产生的空位浓度,辐照产生空位浓度与热力学平衡状态空位浓度2者之和为辐照环境的总空位量。根据Odette等[35]的工作,CVr与辐照强度有关：

式中,GV为每原子离位产生的空位数量,?dpa为辐照产生的原子离位率。可见,在指定材料中CVr直接由辐照强度确定。

GV取决于原子的临界复合半径rV和Vm。在稳态情况下其值由RED模型[35]求解,解析方程为：

式中,Rt为陷阱的复合半径；τt为空位的捕获时间,其取值为：

式中,kB为Boltzmann常数。

将 式(16)整理后,GV的解析表达式如下：

式中,B为整合系数：

将 式(17)带入 式(15),得到CVr,结合 式(13)和(14),获得MR与DR。

1.4 模型的无量纲化

对相场模型进行参数无量纲化处理,得到标注*号的无量纲化参数。无量纲化过程如下：在无量纲空间,位置坐标r* = r / l0,无量纲时间单位t* = tD / l02,无量纲Cu元素的迁移率M${}_{\mathrm{C}\mathrm{u}}^{\mathrm{*}}$ = RT0MCu/ D,无量纲空位的迁移率M${}_{\mathrm{V}}^{\mathrm{*}}$ = RT0MV/ D,无量纲导数符号∇* = ∂ / ∂r*,无量纲自由能G* = G / (RT0),无量纲空位生成率P${}_{\mathrm{V}}^{\mathrm{*}}$ = PVl02 / D,无量纲空位复合率R${}_{\mathrm{V}}^{\mathrm{*}}$ = RVl02 / D,无量纲空位淹没率S${}_{\mathrm{V}}^{\mathrm{*}}$ = SVl02 / D,无量纲界面能扩散系数κ${}_{?″}^{\mathrm{*}}$ = κ${}_{?″}^{}$Vm / (NAl02),无量纲本征弹性应变ε${}_{?″}^{\mathrm{*}}$ = ε${}_{?″}^{}$t2 / Vm。其中,l0为单位长度,取bcc结构铁素体的晶格常数为l0 = Am= 0.287 nm,代表归一化长度单位。T0为计算时选取的温度。归一化后,方程(10)和(11)表示为：

1.5 模型的数值计算方法

约束条件弦方法通过初始条件规定演化方向,用约束条件限制演化目标。与一般的遗传算法相似,约束条件弦方法也需要构建遗传变量的遗传递推方程。本工作使用快速Fourier变换方法对演化方程进行处理[25],所得到的半隐式Fourier方程形式为：

式中,k为Fourier向量空间坐标。在形核模拟中C(i, t)和C(i + 1, t)分别表示在第i轮演化与第i + 1轮演化中弦变量L上时刻t的状态对应的浓度场变量。

将浓度场变量C(i, t)按照 式(22)进行求解,可以得到演化后的弦变量L(i)及对应的N个离散状态点C(i, t),它们对应浓度场信息。本工作中,模拟的物理空间为128 × 128,对应的实际尺寸约为36.7 nm × 36.7 nm。形核过程进行了120个时间节点的计算,N = 120,Δt = 0.001 ms,对应的实际形核时间为0.12 ms,I = 50。

2 结果与讨论

一般认为二元铁素体合金的实际偏析相呈球体[22,36]。当核半径小于临界形核半径时,若无外加能量驱动,Cu元素向内扩散的速率将小于向外扩散的速率,核将趋于消失；反之,若核半径大于临界形核半径,核将进一步长大[37]。因此,计算模拟形核过程的关键在于正确计算临界晶核半径和能量路径。

2.1 最小能量路径与临界形核半径的计算

图2为650 K时Fe-0.3%Cu (质量分数)合金中富Cu团簇的非典型形核过程中的能量路径的变化曲线。纵坐标为体系总能量,横坐标为对应状态数[18]。曲线最左端的点对应Cu元素均匀分布的初始态,最高点对应临界富Cu团簇的状态,最右端对应一定演化时间后的状态。本工作中,将形核过程的每根“弦”分割为120个时间步长,单根“弦”上的每个状态数对应一个时间节点。50轮次弦的演化对应50次形核能量路径的演化。可以看出,能量路径是一个先升高后降低的势垒函数,经过多次演化,形核能量路径的最高值不断降低,这符合弦方法的特征[19,20]。本工作中,在弦不断演化的同时,其对应的能量路径不断逼近最小能量路径,最终实现最小能量路径形核过程的计算。到达势垒最高值所对应的时间,即形核半径长大到达临界形核半径所需要的时间。根据 式(3),某点自由能对浓度的导数将与该点浓度变化率成正相关关系[38],Cu元素浓度和工作温度是影响最小能量路径的主要因素。

图2

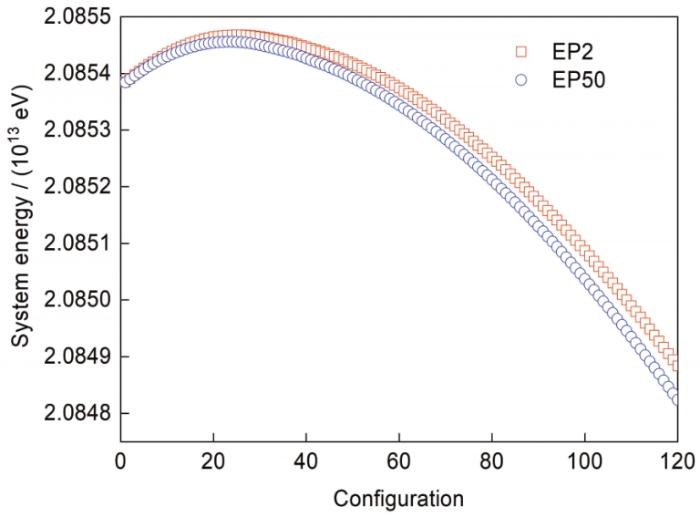
图2   650 K时Fe-0.3%Cu合金在辐照强度0.01 dpa/s下演化2步和50步后的能量路径

Fig.2   Energy paths of Fe-0.3%Cu alloy at 650 K and radiation intensity of 0.01 dpa/s (EP2 for energy path after 2-step-revolution, EP50 for energy path after 50-step-revolution. The abscissa represents the number of nucleus time states, the same in the figures below)

图3为图2中2条曲线能量极大值点所对应的Cu元素浓度分布图。图3中的临界形核半径为势垒状态下所对应的团簇半径,各图右上角的插图为对应团簇的平面俯视图。可以看出,临界核心中心处的Cu元素浓度较高,而在边缘处的Cu元素浓度迅速降低,演化后临界团簇状态发生了明显变化,说明演化改变了形核过程中Cu元素析出的方向和速度。

图3

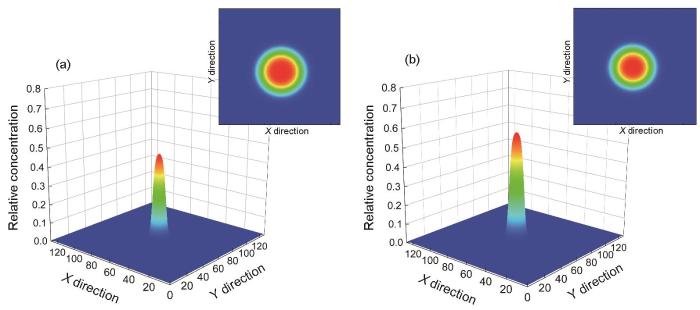
图3   650 K和0.01 dpa/s下Fe-0.3%Cu演化2步和50步后临界团簇的Cu元素浓度分布和团簇形貌

Fig.3   Cu concentration distributions and top views of cluster morphologies of critical nucleus (insets) of Fe-0.3%Cu alloy at 650 K and radiation intensity of 0.01dpa/s

(a) cluster after 2-step-revolution (b) cluster after 50-step-revolution

2.2 温度对形核过程的影响

图4为不同温度下演化50步(I = 50)后Fe-0.3%Cu合金中富Cu相形核的最小能量路径。可以看出,温度对能量路径的影响非常明显。当温度为550 K时(图4a),在模拟时间内没有观察到能量路径的峰值点,而当温度高于600 K时(图4b~d),在模拟时间内观察到了明显的能量路径的峰值。这说明随温度降低形核速率在大幅延缓,形核所需时间大幅延长,表明温度的降低将大大增加形核难度。李博岩[21]的计算结果显示,当温度降低到一定程度,形核势垒将迅速升高到常规热力学手段难以达到的高度,这与本工作计算结果类似。这说明在辐照条件下温度将极大影响形核过程的方向,即Fe-Cu二元合金的富Cu相析出过程具有明显的温度驱动性。

图4

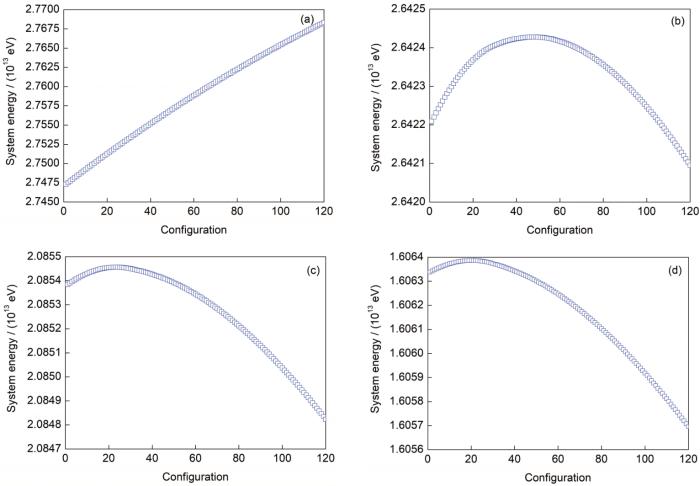
图4   不同温度下演化50步后Fe-0.3%Cu合金的最小能量路径

Fig.4   Minimum energy path curves of Fe-0.3%Cu alloy after 50-step-revolution at 550 K (a), 600 K (b), 650 K (c), and 700 K (d)

图5为不同温度下演化50步后Fe-0.3%Cu合金中富Cu相临界形核状态的团簇信息,核心团簇的半径RC与团簇内Cu元素的平均浓度CC如表4所示,图6为对应的Cu临界形核团簇浓度的一维分布曲线。计算得到的Cu元素团簇临界形核半径为1.722 nm,这与文献[39~41]的计算结果相近。在保持浓度一定的情况下,温度对临界形核半径的影响不大,表现为随着温度从550 K升高至700 K,临界形核半径仅在1.722~1.821 nm之间缓慢提升,但团簇中心的Cu原子浓度的有一定的升高,温度对Fe-Cu合金的富Cu相析出速率和临界形核半径的影响并不明显。

图5

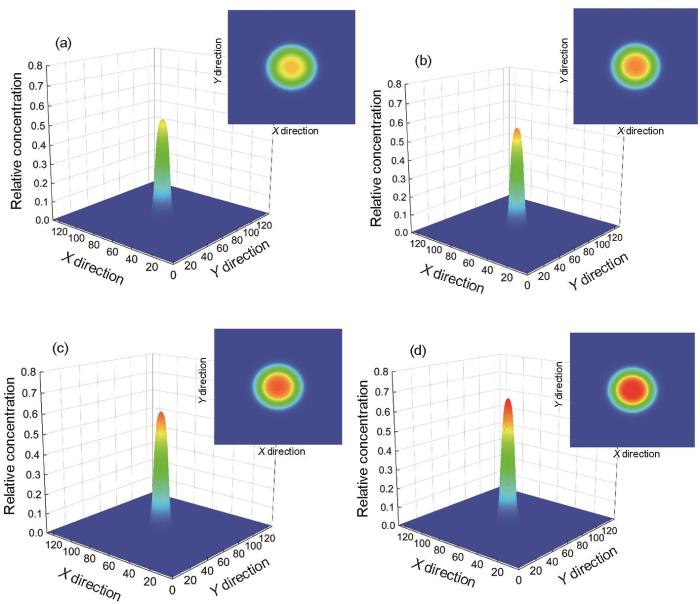
图5   不同温度下演化50步后Fe-0.3%Cu合金临界团簇的Cu元素浓度分布和团簇形貌

Fig.5   Cu concentration distributions and top views of cluster morphologies of critical nucleus (insets) of Fe-0.3%Cu alloy after 50-step-revolution at 550 K (a), 600 K (b), 650 K (c), and 700 K (d)

表4   不同温度下演化50步后Fe-0.3%Cu合金临界团簇半径与浓度计算结果

Table 4  Calculation results of critical nucleus radius (RC) and average Cu concentration in critical nucleus clusters (CC) of Fe-0.3%Cu alloy after 50-step-revolution at different temperatures

新窗口打开| 下载CSV

图6

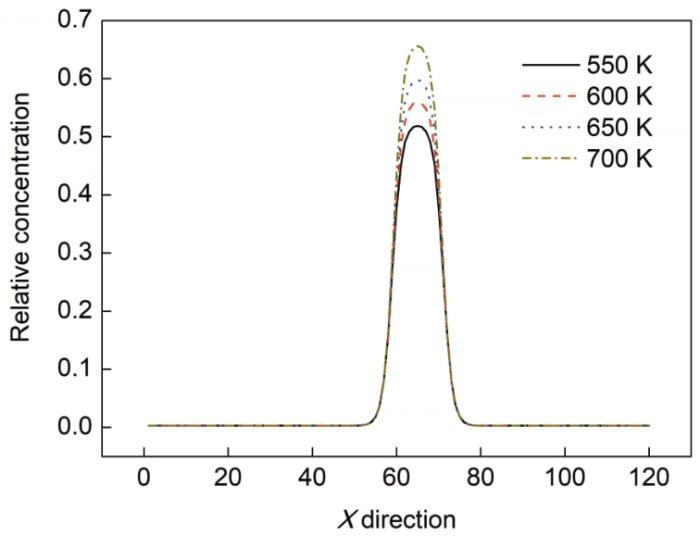
图6   不同温度下演化50步后Fe-0.3%Cu合金临界团簇Cu元素浓度的一维分布曲线

Fig.6   1D Cu concentration distribution curves in critical nucleus cluster of Fe-0.3%Cu alloy after 50-step-revolution at different temperatures

2.3 Cu含量对形核的影响

图7为650 K演化50步后不同Cu元素浓度Fe-Cu合金中的最小能量路径。可以看出,随着Cu元素浓度的增加,形核过程中越过能量势垒的时间变短,但Cu元素浓度对Fe-Cu二元合金形核所需翻越的自由能势垒高度的影响并不明显,表现在4种浓度下合金的自由能均保持在2.08 × 1013 eV附近。可见,Cu浓度的提升为形核提供更大的形核驱动力,呈现为更快形核的趋势[12],提高Fe-Cu合金中Cu元素的浓度可以提高形核速率。

图7

图7   650 K下演化50步后不同Cu元素浓度Fe-Cu合金的最小能量路径

Fig.7   Minimum energy path curves of Fe-Cu alloy after 50-step-revolution with Cu concentrations of 0.05% (a), 0.1% (b), 0.3% (c), and 0.5% (d) at 650 K

图8绘制了650 K下演化50步后Cu元素浓度为0.05%、0.1%、0.3%和0.5%时临界团簇的Cu元素浓度分布和团簇形貌,计算的浓度数值如表5所示,图9为图8中临界形核团簇的Cu元素浓度的一维分布曲线。可以看出,在温度一定的情况下,Cu元素浓度对临界团簇半径的影响比较明显。Cu浓度越高,团簇中心浓度和团簇半径的生长速率越高。当Cu元素浓度较低时(0.05%和0.1%),临界团簇尚没有形成均匀分布的稳定晶核。而在初始Cu浓度相对较高的情况下(0.3%和0.5%),相对稳定浓度的核心已经形成。

图8

图8   650 K下演化50步后不同Cu元素元素浓度Fe-Cu合金临界团簇的Cu元素浓度分布和团簇形貌

Fig.8   Cu concentration distributions and top views of cluster morphologies of critical nucleus (insets) of Fe-Cu alloy after 50-step-revolution with Cu concentrations of 0.05% (a), 0.1% (b), 0.3% (c), and 0.5% (d) at 650 K

表5   650 K下演化50步后不同Fe-Cu合金的临界团簇半径与平均浓度计算结果

Table 5  Calculation results of RC and CC for different Fe-Cu alloys at 650 K after 50-step-revolution

新窗口打开| 下载CSV

图9

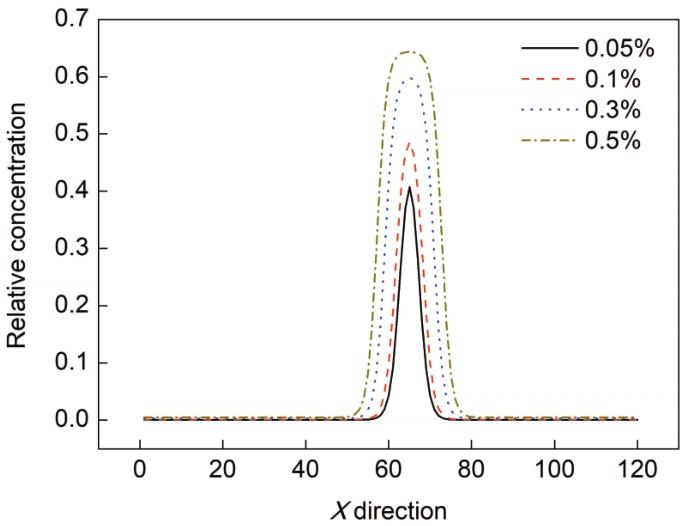
图9   650 K下演化50步后不同Fe-Cu合金临界团簇中Cu元素浓度的一维分布曲线

Fig.9   1D Cu concentration distribution curves in critical nucleus clusters of Fe-Cu alloy with different Cu concentrations at 650 K after 50-step-revolution

图10为不同温度和不同Cu元素浓度下演化50步后的中心团簇半径变化曲线。可以看出,Cu原子浓度差异对富Cu相团簇半径的长大速率有很大影响(图10a)。在不同的温度和Cu元素浓度下,中心团簇半径的增长速率均呈随时间演化而放缓的趋势。这是由于随团簇半径的逐渐增大,团簇与周围的接触面积也在逐渐增大,原子数量的增长速率将逐渐放缓,存在形核极限尺寸[42]。可见,Cu元素浓度变化对核心团簇半径的成长速率有较为明显的影响,而温度的升高对核心团簇成长速率,尤其是达到一定的核心团簇尺寸后的生长速率影响不大。

图10

图10   不同温度和不同Cu元素浓度下演化50步后团簇半径的变化曲线

Fig.10   Changes of cluster radius for Fe-Cu alloy after 50-step-revolution

(a) 650 K for different Cu concentrations

(b) 0.3%Cu concentration at different temperatures

2.4 辐照剂量对空位产生与分布的影响

辐照空位的产生与材料成分、辐照强度有关,而与温度关系不明显。在材料中存在空位产生、空位与间隙原子复合、空位被晶界或其他缺陷吸收3种效应。

图11为650 K下演化50步后在辐照强度分别为0.01和0.05 dpa/s下Fe-0.3%Cu和Fe-0.5%Cu合金在临界团簇状态下的空位增量分布图。其中0.01 dpa/s时Fe-0.5%Cu合金富Cu团簇中的空位相对浓度增加量最少,为3.006 × 10-5；0.05 dpa/s时Fe-0.3%Cu合金富Cu团簇的空位相对浓度增加量最多,为3.15 × 10-5。可以看出,与基体中空位浓度的增加值相比,富Cu团簇中的辐照空位浓度增加量较少。可见,辐照条件下空位浓度的变化受Cu含量的影响较大。而提高辐照强度后,基体和富Cu团簇中的空位浓度均有所提高。

图11

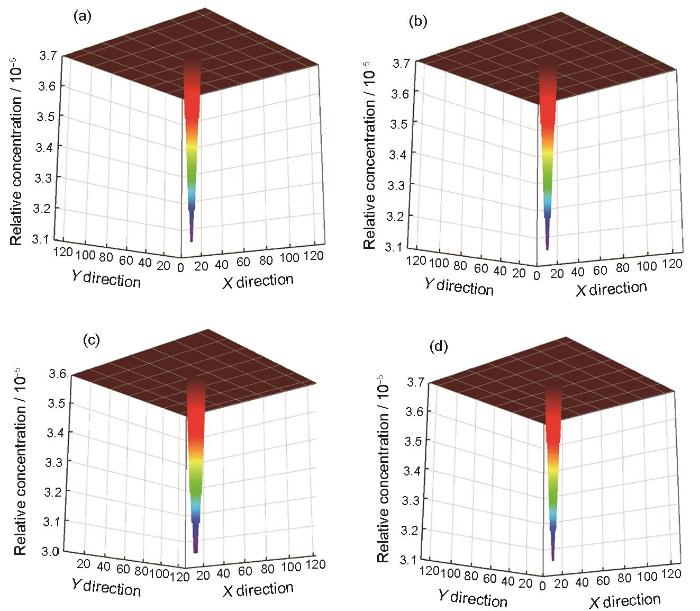
图11   650 K下演化50步后不同辐照强度下Fe-0.3%Cu和Fe-0.5%Cu合金临界团簇状态的空位增量分布图

Fig.11   Distributions of the increase of vacancy concentration at critical nucleus cluster state after 50-step-revolution at 650 K

(a) Fe-0.3%Cu, 0.01 dpa/s (b) Fe-0.3%Cu, 0.05 dpa/s

(c) Fe-0.5%Cu, 0.01 dpa/s (d) Fe-0.5%Cu, 0.05 dpa/s

图12为650 K下演化50步后0.01 dpa/s的辐照条件下Fe-0.3%Cu合金在不同时刻的空位浓度分布图,对应的不同时刻的空位浓度的最大值、最大最小值之差和空位量总数等信息如表6所示。结果显示,随着形核的进行,区域内空位总数逐渐增加,而团簇外的均匀浓度部分空位浓度基本保持不变。随形核的进行,空位产生速率逐渐降低,团簇中心与未形核区域的空位浓度差距逐渐拉大,这说明Cu元素偏析效应将导致空位所在空间范围内的空位生成数量减少。

图12

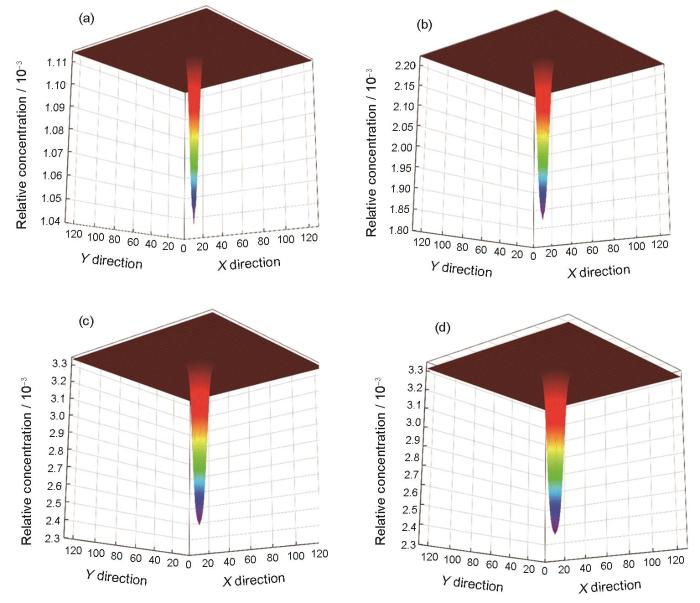
图12   650 K下演化50步后辐照强度0.01 dpa/s下Fe-0.3%Cu合金在不同时刻的空位浓度分布

Fig.12   Vacancy concentration distributions after 50-step-revolution at the different time (t) of nucleus of Fe-0.3%Cu alloy at 650 K and 0.01 dpa/s

(a) t = 30 step (b) t = 60 step (c) t = 90 step (d) t = 120 step

表6   演化50步后不同时刻下团簇空位浓度信息计算结果

Table 6  Calculation results of partial parameters of critical nucleus clusters after 50-step-revolution at different t

新窗口打开| 下载CSV

3 结论

(1) 建立了结合辐照空位形成的Fe-Cu二元合金Cu元素析出的相场模型,结合约束条件弦方法对辐照条件下Fe-Cu合金中富Cu相形核过程进行了计算,得到了在多种温度和初始浓度下Cu元素形核过程临界形核状态的纳米尺寸Cu元素团簇物理参数、形核过程能量路径、空位分布等参数,计算结果与实验结果基本符合。

(2) 温度和Cu含量对Fe-Cu二元合金中富Cu相析出过程的能量路径和临界形核尺寸有明显影响。其中,温度是影响形核能量路径走向的主要因素,浓度是影响临界形核半径生长速率的主要因素。温度越高,Cu含量越高,形核达到临界形核尺寸所需要的时间越短,所需要超越的能量势垒越低,与实验观察结果一致。

(3) Cu元素浓度场的分布对辐照空位浓度的分布也有很大的影响。Cu元素含量越高,相同辐照条件下空位浓度越低,且空位的分布越不均匀。在富Cu团簇中的空位浓度比Fe-Cu基体更低,而且Cu浓度越高,空位的浓度越低。