分享：变形速率对GH3625合金弹-塑性变形行为的影响

高钰璧1,2,3, 丁雨田,1,2, 李海峰4, 董洪标,5, 张瑞尧6, 李军5, 罗全顺3

GH3625合金在低温到980℃具有高强度、高韧性以及优良的耐疲劳性能和抗Cl-应力腐蚀能力,已广泛应用于航空发动机、燃气轮机和核电设备等关键部件中[1~3]。作为典型的多晶体材料,它的力学响应取决于其单晶性质、晶体的晶格取向和相邻晶体取向[4]。因此,准确测定单晶性质对于多晶体材料整体的微观力学行为的定量理解至关重要。

目前,国内外关于GH3625合金变形行为的研究主要通过宏观拉伸/压缩应力-应变曲线和微观组织分析相结合的方式,如闫士彩等[5]采用热压缩应力-应变曲线和微观组织分析相结合的方法研究了Inconel 625合金在1000~1200℃,应变速率为10~80 s-1条件下的热变形行为。Li等[6]采用热压缩实验与电子背散射衍射(EBSD)和透射电子显微镜(TEM)技术相结合,研究了Inconel 625合金在900~1200℃,应变速率为0.1 s-1条件下的热变形行为。Badrish等[7]采用准静态拉伸应力-应变曲线研究了Inconel 625合金在室温到600℃,应变速率为0.0001~0.1 s-1条件下的各向异性行为。Rodriguez等[8]采用单轴拉伸及蠕变实验与扫描电子显微镜(SEM)和TEM技术相结合,研究了球磨Inconel 625合金的拉伸和蠕变行为。本课题组前期工作[9~11]采用准静态室温压缩应力-应变曲线和微观组织分析相结合,研究了GH3625合金的冷变形行为。但是,上述GH3625合金的宏观应力-应变曲线均不能直接反映该合金的细观弹-塑性变形行为。

中子衍射技术是当前研究材料微观力学行为的成熟技术[12,13]。由于中子衍射原位拉伸/压缩实验可以得到材料在受载情况下特定(hkl)晶面的晶格应变,从而研究材料的微观力学行为。Wong和Dawson[4]通过中子衍射原位拉伸实验研究了fcc结构多晶体材料中晶体各向异性对晶格应变所表现的弹-塑性转变行为的影响。Daymond和Bouchard[14]通过中子衍射原位拉伸实验研究了316不锈钢高温弹-塑性变形行为,发现在传统的滑移过程中以及动态应变时效的过程中,实验结果与基于滑移的弹性自洽模型结果均获得了良好的一致性。Lee等[15]通过中子衍射原位压缩实验研究了难熔高熵合金的弹性和塑性变形行为的温度依赖性,晶格应变演变结果表明合金具有独特的弹性变形行为,即在室温下表现为弹性各向同性,而在高温下表现为弹性各向异性,与常规金属材料相比,合金的弹性各向异性变形行为对温度的依赖性较小。Wang等[16]通过中子衍射原位压缩实验测定了室温和高温下Inconel 625合金的衍射弹性常数和单晶弹性常数。但已有的报道很少利用原位中子衍射技术对GH3625合金的细观弹-塑性变形行为进行系统性研究。

鉴于此,本工作采用原位中子衍射技术实时测量GH3625合金室温压缩变形过程中各个(hkl)晶面的晶格应变、峰宽和强度的演变,研究变形速率对合金弹-塑性变形行为的影响,利用EBSD和TEM技术对原位中子衍射测量后试样的微观组织进行分析,结合位错密度理论计算,揭示了GH3625合金的塑性变形机制和加工硬化机制,阐明了合金在低变形速率下反常加工硬化行为的机制。

1 实验方法

GH3625合金棒材的化学成分(质量分数,%)为：Cr 21.77,Mo 8.79,Nb 3.75,Fe 3.68,Ti 0.40,Al 0.21,C 0.042,P 0.006,S 0.0006,Ni 余量。试样从热挤压棒材上切取,经1150℃保温1 h + 空冷的固溶处理后机加工成直径12 mm、长32 mm的圆柱试样,在室温下进行原位压缩实验。

在ENGIN-X中子衍射仪上进行压缩变形过程中的原位衍射测量[17]。将样品水平安装在Instron应力装置上,其加载轴(平行于压缩方向)与入射中子束成45°。衍射仪上的2个接收器(Bank 1和Bank 2)收集散射角2θ = ±90°的衍射信号,散射矢量(scattering vector)分别平行于和垂直于样品的加载方向。以分步方式压缩样品,在每个步骤收集中子衍射数据。在压缩实验中应用2种不同的加载方法。首先,将样品在应力控制下以50 MPa的步长和10 MPa/s的速率压缩至350 MPa。然后,在位移控制下使样品变形,从而实现特定的压缩速率。在位移控制变形过程中分别以0.2、0.5和1.0 mm/min的变形速率(r)测试样品,研究变形速率对合金细观弹-塑变形行为的影响。使用Open Genie软件包分析衍射光谱,该软件包提供晶面间距(d)、衍射峰强度(I)和半峰全宽(FWHM)的信息。

所有原位中子衍射压缩实验后的试样呈S型,这与压缩变形过程中的自由变形和晶粒转动有关。在纯切应力作用下,晶体的滑移不会引起取向的改变,但晶体在发生塑性变形时,不仅仅只受纯切应力的作用,还存在压应力等作用力,压缩过程中夹头不受限制,则经外力(F)轴向压缩,为了保持滑移面的滑移方向不变,力轴将会发生偏移[18]。在压缩变形过程中是否发生晶粒转动通过详细的中子衍射和EBSD进行分析。将压缩后的试样使用线切割方法沿轴向中心剖开,对剖面(LD-TD,LD和TD分别为圆柱试样的轴向和横向)进行研磨、机械抛光后,用20%H2SO4 + 80%CH3OH (体积分数)电解液进行电解抛光,直流电压20 V,抛光时间30 s,利用配有HKL-EBSD探头的Quanta FEG 450型热场发射SEM进行EBSD分析,使用Channel 5软件进行数据处理。在压缩变形后的试样中以距离表面3 mm处为圆心切割出厚度为3 mm的圆片,然后将其用砂纸打磨至厚度50 μm左右,在Gatan 695型离子减薄仪上进行离子减薄,然后在Talors F200 TEM上进行测试,测试电压为200 kV。

2 实验结果与分析

2.1 宏观应力-应变曲线

图1为GH3625合金在不同变形速率下的压缩应力-应变曲线和加工硬化率曲线。从图1a中可以看出,在不同的变形速率下合金的压缩应力-应变曲线均分为3个阶段：第1阶段为弹性变形阶段(σ ≤ 300 MPa,σ为施加应力),第2阶段为弹-塑性转变阶段(300 MPa < σ ≤350 MPa),第3阶段为塑性变形阶段(σ > 350 MPa),其中图1a曲线上锯齿代表位移控制下(保持应变)的应力释放现象。在第1阶段中,应变随施加应力的增加呈线性响应(图1a),加工硬化率在初始阶段发生轻微改变(图1c中插图),属于典型的弹性变形特征。在此阶段,所有试样的屈服强度均为300 MPa,变形速率对合金的屈服强度没有影响,说明合金的屈服强度依赖于合金的原始晶粒尺寸；但变形速率对合金的弹性模量(E)有轻微的影响(图1b),这可能与晶体弹性各向异性有关[19]。在第2阶段中,应变随施加应力的增加出现“台阶”状,呈非线性响应,而加工硬化率急剧下降后突然增加,出现弹-塑性转变点(图1b和d中a、b和c分别对应变形速率为0.2、0.5和1.0 mm/min时的弹-塑性转变点),说明此阶段出现短暂的弹-塑性转变[20]。在此阶段,施加应力相同的条件下,台阶宽度随变形速率的增加先增加后减小(图1b和d中A、B和C分别对应变形速率为0.2、0.5和1.0 mm/min时的弹-塑性转变阶段的宽度),说明合金的收缩量随变形速率的增加先增加后减小,收缩量越小代表加工硬化越大。在第3阶段中,弹-塑性转变点后应变随施加应力的增加又呈线性响应,加工硬化率随应变的增加缓慢下降。在此阶段,应变相同的条件下加工硬化率随变形速率的增加先减小后增加(图1d),这与GH4738和GH4169合金冷压缩变形时加工硬化率随变形速率的增加而增加的结果不符[20,21],这可能与均匀变形产生的统计存储位错(SSD)对加工硬化做出了额外贡献有关[22]。由此可知,变形速率对GH3625合金弹-塑性变形行为均有影响,在弹性变形阶段影响较小,而在塑性变形阶段影响显著；同时,试样在r = 0.2 mm/min时表现出反常的加工硬化行为。

图1

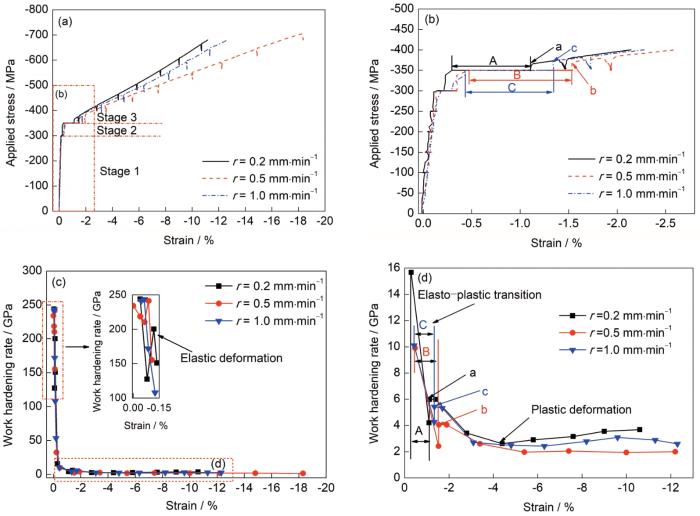
图1   GH3625合金在不同变形速率(r)下的压缩应力-应变曲线和加工硬化率曲线

Fig.1   Compression stress-strain curves (a, b) and work hardening rate curves (c, d) of GH3625 alloy at different deformation rates (r) (Inset in Fig.1c show the locally enlarged work hardening rate curve of alloy elastic deformation stage at different deformation rates; A, B, and C represent the widths of the alloy elasto-plastic transition stage at different deformation rates in Figs.1b and d, while a, b, and c are the elasto-plastic transition points at different deformation rates; The sawtooth on the curve in Fig.1a represents the stress relaxation phenomenon under displacement-control mode (holding strain))

2.2 中子衍射

2.2.1 晶格演变

图2为GH3625合金在不同变形速率下的中子衍射图谱。由图可知,在不同的变形速率下合金在弹-塑性变形过程中均未检测到明显的新衍射峰出现,表明GH3625合金在不同变形速率下压缩变形过程中均未发生相变。同时,在不同的变形速率下合金的衍射峰位置随着施加应力或应变的增加均向低晶面间距发生偏移,如表1~3所示。利用原位中子衍射压缩实验可以得到材料在受载荷情况下的晶格应变来研究材料的性能。加载过程中特定的{hkl}晶面族的晶格应变(εhkl )可以通过衍射峰位置的相对偏移来表达[23]：

图2

图2   不同变形速率下GH3625合金压缩变形过程中的中子衍射图演变

Fig.2   Evolutions of neutron diffraction patterns of GH3625 alloy during compression deformation at r = 0.2 mm/min (a), r = 0.5 mm/min (b), and r = 1.0 mm/min (c) (d—interplanar spacing)

表1   r = 0.2 mm/min时不同应力/应变、不同(hkl)晶面上GH3625合金的晶面间距(d)、衍射峰强度(I)和半峰全宽(FWHM)

Table 1  d, diffraction peak intensity (I), and full width at half maximum (FWHM) of GH3625 alloy at different stresses/strains and different (hkl) crystal planes under r = 0.2 mm/min

新窗口打开| 下载CSV

表2   r = 0.5 mm/min时不同应力/应变、不同(hkl)晶面上GH3625合金的d、I和FWHM

Table 2  d, I, and FWHM of GH3625 alloy at different stresses/strains and different (hkl) crystal planes under r = 0.5 mm/min

新窗口打开| 下载CSV

表3   r = 1.0 mm/min时不同应力/应变、不同(hkl)晶面上GH3625合金的d、I和FWHM

Table 3  d, I, and FWHM of GH3625 alloy at different stresses/strains and different (hkl) crystal planes under r = 1.0 mm/min

新窗口打开| 下载CSV

式中, ${?}_{???}$和 ${?}_{???}^{\mathrm{0}}$分别是{hkl}晶面族加载状态下的晶面间距和无载荷状态下的晶面间距。在本工作中, ${?}_{???}^{\mathrm{0}}$为{hkl}晶面族在5 MPa下的晶面间距。

图3为不同变形速率、不同(hkl)晶面上GH3625合金晶格应变与施加应力的关系。由图3可知,在相同施加应力下,所有试样均在(200)晶面上具有最大的晶格应变,其次从大到小依次是(311)、(220)和(111)晶面上,说明晶格应变的变化很大程度上取决于晶粒取向,表明强弹性各向异性。在弹性变形阶段,所有晶粒在加载方向上的晶格应变均随施加应力的增加呈线性增加,在此阶段,通过施加应力与晶格应变函数的斜率可以计算出每个(hkl)晶面的弹性模量Ehkl,其值列于表4中。由表4可知,所有试样均在(111)晶面上表现出最大的弹性模量,其次是(220)和(311)晶面,而在(200)晶面上最小。这表明(111)晶面具有较大的刚度,而(200)晶面具有较小的刚度,表现出在相同的施加应力下(200)晶面的晶格应变大于(111)晶面的晶格应变。同时,不同变形速率下特定(hkl)晶面的Ehkl 略有差异,这与不同应变速率下宏观应力-应变曲线中弹性变形阶段的整体弹性模量轻微变化相符(图1b)。fcc结构金属的弹性各向异性又称为Young's模量各向异性(rE = E111/ E200),即通过<111>方向的Young's模量与<200>方向Young's模量之比来描述[4,24,25]。计算可知,3种变形速率下试样的rE 分别约为1.75 (r = 0.2 mm/min)、1.80 (r = 0.5 mm/min)和1.74 (r = 1.0 mm/min),其结果介于退火态(1.53)和沉积态(2.24) IN625合金之间[16]。在屈服点之后开始发生塑性变形,所有试样的晶格应变在弹-塑性转变过程中出现向下的弯曲,对应在整体应力-应变曲线中发生了弹-塑性转变(图1a和b)。在此阶段,(200)晶面的晶格应变明显高于其他(hkl)晶面表现出的晶格应变,说明(200)晶面在弹-塑性转变过程中通过充分发展可塑性表现出更大的晶格应变[26]。当施加应力大于350 MPa时,所有(hkl)晶面的晶格应变随施加应力的增加又呈现出近线性相应,其斜率均高于弹性变形阶段。这是由于在塑性变形阶段所有的晶粒都发生塑性变形时,反射的晶格应变响应又几乎变为线性,其斜率由材料的弹性和塑性各向异性共同决定[27]。值得注意的是,在塑性变形阶段,相同的施加应力下,r = 0.2 mm/min的试样所有晶粒的晶格应变均大于其他变形速率的试样,这可能与晶粒取向有关[28]。

图3

图3   不同变形速率、不同(hkl)晶面上GH3625合金晶格应变与施加应力的关系

Fig.3   Lattice strain as a function of applied stress for GH3625 alloy at different deformation rates and different (hkl) crystal planes

(a) (111) crystal plane (b) (200) crystal plane

(c) (220) crystal plane (d) (311) crystal plane

表4   不同变形速率下GH3625合金的弹性模量(Ehkl )和Young's模量各向异性(rE )

Table 4  Elastic moduli (Ehkl ) and Young's Modulus anisotropies (rE ) of GH3625 alloy under different deformation rates

新窗口打开| 下载CSV

2.2.2 衍射峰强度演变

图4为不同变形速率和不同(hkl)晶面上GH3625合金压缩变形过程中的衍射峰积分强度(I / I0)演变。在图4中,衍射峰积分强度通过宏观塑性变形开始时测得的衍射峰强度(I0)进行归一化获得。衍射峰积分强度的变化可以为塑性变形过程中晶粒取向(织构)的变化提供定性的解释[29]。在弹性变形阶段,所有试样在不同(hkl)衍射峰强度基本保持不变,而在弹-塑性转变阶段和塑性变形阶段均表现出相同的变化趋势,但具体增加或减小的数值不同。这表明在塑性变形过程中所有试样在相同(hkl)晶面上形成的织构类型一样,但其强度有明显差异。由图4a可知,所有试样(111)衍射峰积分强度在弹-塑性转变阶段随施加应力的增加而增加,而在塑性变形阶段随施加应力的增加而减小；由图4b可知,所有试样(200)衍射峰积分强度在弹-塑性转变阶段随施加应力的增加而增加,而在塑性变形阶段随施加应力的增加出现先减小后增加的趋势,其施加应力拐点随变形速率的增加而依次减小；由图4c可知,所有试样(220)衍射峰积分强度随施加应力的增加呈现缓慢增加的趋势；由图4d可知,所有试样(311)衍射峰积分强度随施加应力的增加而减小。分析认为,衍射峰强度的增加表明在塑性变形过程中晶粒沿着加载方向重新取向,而衍射峰强度的减小意味着在塑性变形过程中晶粒发生转动,偏离加载方向[29]。值得注意的是,r = 0.2 mm/min的试样衍射峰积分强度的增量均比其他试样的小,减量均比其他试样的大。这表明r = 0.2 mm/min时在变形过程中晶粒发生重新取向的概率远远小于晶粒发生转动的概率。在不同变形速率下,试样的衍射峰强度演化出现明显差异,说明在不同变形速率下压缩变形过程中晶粒重新取向的程度不同,这可能是由于晶粒的滑移/转动和/或形成形变孪晶造成的[30,31]。

图4

图4   不同变形速率、不同(hkl)晶面上GH3625合金压缩变形过程中的衍射峰强度演变

Fig.4   Evolutions of diffraction peak intensity of GH3625 alloy during compression deformation at different deformation rates and different (hkl) crystal planes

(a) (111) crystal plane (b) (200) crystal plane (c) (220) crystal plane (d) (311) crystal plane

2.2.3 衍射峰宽度演变

图5为不同变形速率和不同(hkl)晶面上GH3625合金压缩变形过程中的衍射峰归一化宽度(W / W0)演变。在图5中,衍射峰归一化宽度通过宏观塑性变形开始时测得的衍射峰FWHM (W0)进行归一化获得。在多晶体合金中,衍射峰宽度的演变与合金在变形过程中形成的位错、层错和孪晶密切相关[32]。在弹性变形阶段,所有试样不同(hkl)衍射峰宽度基本保持不变,而在弹-塑性转变阶段和塑性变形阶段均表现出明显的上升趋势,但其增量不同。所有试样(200)衍射峰宽度的增量最大,其次从大到小依次是(311)、(220)和(111)衍射峰,表明在压缩变形过程中不同(hkl)晶粒变形行为不同,这很大程度上取决于晶粒取向。

图5

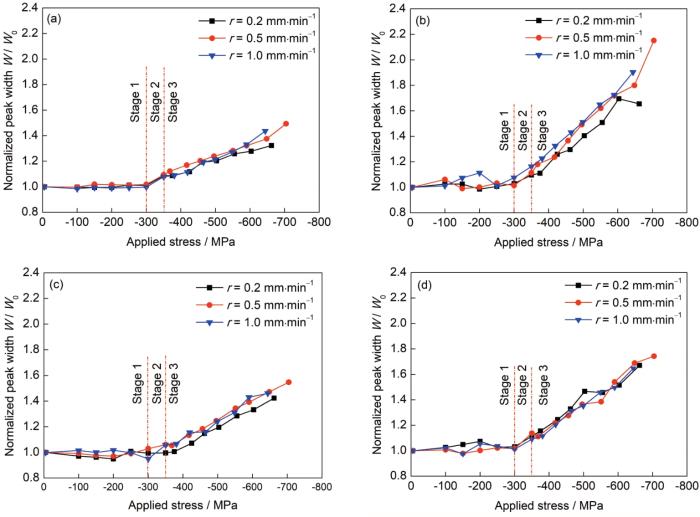
图5   不同变形速率、不同(hkl)晶面上GH3625合金压缩变形过程中的衍射峰宽化演变

Fig.5   Evolutions of diffraction peak width of GH3625 alloy during compression deformation at different deformation rates and different (hkl) crystal planes

(a) (111) crystal plane (b) (200) crystal plane (c) (220) crystal plane (d) (311) crystal plane

2.3 组织演变与晶界特征演变

为了进一步研究变形速率对合金塑性变形行为的影响,揭示合金的塑性变形机制和加工硬化机制,对中子衍射测量后的试样进行EBSD和TEM分析。图6为GH3625合金在不同变形速率下的显微组织及其应变分布特征,其中,灰线表示小角度晶界(2° < θ ≤15°),而黑线表示大角度晶界(θ > 15°)。可以看出,GH3625合金原始组织由大量均匀的等轴晶粒和少量的退火孪晶组成(图6a)；同时,可以通过kernel平均取向差(kernel average misorientation,KAM)的分布来定量评估材料的局部应变分布[33,34],图6中的插图为KAM图,其中蓝色表示低应变区,红色表示高应变区。由图6a插图可知,应变均匀分布在晶界处和晶粒内部。当变形速率较小时(r = 0.2 mm/min),等轴晶粒被压扁,变形不明显,小角度晶界优先在晶界附近分布,并伴随位错滑移产生局部应变集中；当变形速率较大时(r ≥ 0.5 mm/min),等轴晶粒受压缩变形开始呈现扁平状,晶界附近小角度晶界明显增多,晶粒内部出现大量的小角度晶界,晶粒内部出现应变集中,晶界处应变集中逐渐增强。此外,为了直观描述变形速率对不同类型晶界特征分布的影响,采用取向差角分布来表征晶界特征演变。图7为不同状态下GH3625合金的取向差角分布演变。可以看出,原始试样的取向差角分布呈双峰分布,一个峰在1.5°附近,另一个峰在60°附近(图7a),而变形试样的取向差角分布呈单峰分布,其峰1.5°在附近(图7b~d)。显然,低角度峰对应于大量位错缠结形成的几何必要位错(GND)界面[35],而位于60°附近的峰对应于退火孪晶[36]。同时,统计晶界比例可知,原始试样的晶界以大角度晶界为主,占整个晶界的60.37%；当以r = 0.2 mm/min开始变形时,晶界以小角度晶界为主,占整个晶界的84.61%,随着变形速率的增加,小角度晶界的比例增加,而大角度晶界和孪晶界的比例减小。孪晶界的减少是因为在塑性变形期间主要以滑移方式进行,堆积在孪晶界附近的小角度晶界与孪晶界合并为随机晶界[37]。可见,随变形速率的增加,大角度晶界逐渐向小角度晶界转变,孪晶界的比例减小,晶粒由均匀变形向不均匀变形转变。

图6

图6   不同状态下GH3625合金的微观组织及其应变分布特征演变

Fig.6   Evolutions of microstructure and strain distribution characteristics in GH3625 alloy under different states (TD—transverse direction, LD—longitudinal direction, TBs—twin boundaries; gray lines show the low angle grain boundaries (LAGBs), black lines show the high angle grain boundaries (HAGBs); Insets show the kernel average misorientation (KAM) images of rectangle regions)

(a) solution state (b) r = 0.2 mm/min (c) r = 0.5 mm/min (d) r = 1.0 mm/min

图7

图7   不同状态下GH3625合金的取向差分布演变

Fig.7   Evolutions of misorientation angle distribution of GH3625 alloy under different states (fLAGB—fraction of LAGB, fHAGB—fraction of HAGB, fTB—fraction of TB)

(a) solution state (b) r = 0.2 mm/min (c) r = 0.5 mm/min (d) r = 1.0 mm/min

图8为GH3625合金在0.5 mm/min变形速率压缩变形后组织的TEM像。由图可知,晶粒内部存在大量位错线相互交叉形成的位错网(图8a)、位错通过相互作用形成位错缠结(图8b)以及晶界处存在大量位错塞积(图8c),可见晶界是位错运动的障碍；此外,晶粒内部出现条带状结构,终止于晶界(图8c)。图8c插图中选区电子衍射(SAED)花样说明条带状结构为变形带,而不是变形孪晶。分析认为,由于GH3625合金属于典型的fcc结构的低层错能材料,合金冷变形开始时,不全位错开始滑移变形,当变形量达到一定程度时,合金还会发生孪生变形,在晶粒内部产生变形孪晶[38]。然而,由于本工作中变形量较小,未达到孪生变形的条件,因此在晶界处由于压缩变形不均匀引起位错塞积,导致位错运动的阻力增加,造成明显的加工硬化现象。可见,GH3625合金在冷塑性变形过程中主要以位错滑移的方式进行,其加工硬化机制以位错强化为主。

图8

图8   GH3625合金在0.5 mm/min变形速率压缩变形后组织的TEM像

Fig.8   TEM images showing the microstructures of GH3625 alloy after compression deformation at r = 0.5 mm/min

(a) dislocation network(b) dislocation tangle(c) grain (Inset in Fig.8c shows the SAED pattern of deformation band )

2.4 位错密度

金属塑性变形在微观上反映了位错的形成、增殖和运动,在宏观上表现为金属的加工硬化行为。根据Ashby的位错演化模型[39],多晶金属材料在塑性变形过程中可以将位错分为统计存储位错(SSD)和GND,即：

式中,ρ为多晶金属材料的总位错密度,ρSSD为多晶金属材料的SSD密度,ρGND为多晶金属材料的GND密度。SSD是由均匀变形引起的,而GND是由不均匀变形引起的。GH3625合金在压缩变形过程中由不均匀变形引起的ρGND可以通过应变梯度来计算[40,41]:

式中,θL为局部取向差,μ为该点的单位长度(100 nm),b为Burger矢量模(0.253 nm)。根据 式(3)得到不同变形速率下GH3625合金的ρGND分布和平均ρGND如图9所示。由图可知,ρGND随变形速率的增大而增加,再次证明了变形速率的增加使得合金压缩变形不均匀引起的应变集中程度增强。

图9

图9   GH3625合金不同状态下的几何必须位错密度(ρGND)分布和平均ρGND

Fig.9   Geometrically necessary dislocation density (ρGND) distribution (a) and average ρGND (b) of GH3625 alloy under different states

GH3625合金在压缩变形时由变形产生的总位错密度ρ可以用材料中的弹性能(U)、单位位错长度的弹性能(u)与平均衍射峰宽化ΔW / d来表示[42,43],计算公式为：

式中,G为剪切模量,v为Poisson比,ε为平均晶格应变。在本工作中,GH3625合金在室温下的E = 205 GPa,G = 79 GPa,v = 0.308,b = 0.253 nm[44]。根据 式(4)得到不同变形速率下GH3625合金总位错密度随应变的变化规律如图10a所示。由图可知,在屈服点之前,所有试样的ρ与应变呈线性关系,不随变形速率的变化而变化；在屈服点之后,相同应变下合金的ρ随变形速率的增加先减小后增加,这与整体宏观应力-应变曲线中塑性变形阶段加工硬化相符(图1a)。不同变形速率下GH3625合金加工硬化位错强化的贡献如图10b所示。由图可知,在塑性变形阶段,随着应变的增加,所有试样的ρ1/2与σ之间的关系均符合Taylor关系(σ = αMGbρ1/2,其中α为常数,M是Taylor因子)[45],说明在不同变形速率下GH3625合金加工硬化主要由位错强化来决定。

图10

图10   不同变形速率下GH3625合金的总位错密度(ρ)随应变的变化规律和位错强化贡献

Fig.10   Variations of total dislocation density (ρ)with strain for GH3625 alloy at different defor-mation rates (a) and contribution of dislocation strengthening (b)

GH3625合金在不同变形速率下压缩变形后的ρ与ρGND之间存在差值,其差值ρSSD可以由 式(2)来表示。表5为不同变形速率下GH3625合金压缩变形后ρ、ρGND和ρSSD的变化规律。可知,ρSSD随变形速率的增加而减小,而ρGND随变形速率的增加而增加,说明变形速率越小,其变形均匀性越好。可见,r = 0.2 mm/min时合金表现出反常的加工硬化行为归因于较低变形速率下塑性变形过程中均匀变形产生的SSD对加工硬化做出了额外的贡献[22]。

表5   不同变形速率下GH3625合金压缩变形后的ρ、ρGND和统计存储位错密度(ρSSD) (1014 m-2)

Table 5  ρ, ρGND, and statistically stored dislocation density (ρSSD) of GH3625 alloy after compression deformation under different rates

新窗口打开| 下载CSV

2.5 织构演变

图11的取向分布函数(ODF)截面图展现出了不同状态下GH3625合金在变形过程中织构变化规律。由图11a可知,固溶态试样在α取向线上出现Rotated-Goss织构{110}<110>和Brass织构{110}<112>,在γ取向线上出现Brass-R织构{111}<110>和{111}<112>。在较小变形速率(r = 0.2 mm/min)下,由于变形速率较小,晶粒变形比较均匀,因此不会出现由不均匀变形产生的Rotated-Cube织构{001}<110>；同时,具有Twinned-Copper织构{552}<115>的晶粒经正常的位错滑移流向Goss织构{110}<001>[46],如图11b所示。在较大变形速率(r ≥ 0.5 mm/min)下,由于变形速率较大,晶粒变形不均匀,导致在压缩变形过程中出现了较强的Rotated-Cube织构{001}<110>；同时,由于剪切变形出现Rotated-Copper织构{112}<110>；此外,还会保留原始的Brass-R织构{111}<110>和Rotated-Goss织构{110}<110> (图11c和d)。结合衍射峰积分强度分析可知,随着变形速率的增加,{001}面上的晶粒发生转动后重新取向形成Rotated-Cube织构{001}<110>,而{110}面上的部分晶粒通过位错滑移后重新取向形成Goss织构{110}<001>；同时,{110}面上部分晶粒保留Rotated-Goss织构{110}<110>；此外,{111}面上晶粒发生转动后Brass-R织构{111}<112>消失,仅保留Brass-R织构{111}<110>。

图11

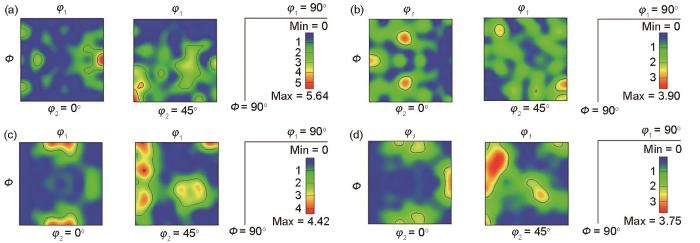
图11   不同状态下GH3625合金的晶粒取向分布函数(ODF)截面图

Fig.11   Orientation distribution function (ODF) sections of GH3625 alloy under different states (Φ, φ1, and φ2—Euler angles)

(a) solution state (b) r = 0.2 mm/min (c) r = 0.5 mm/min (d) r = 1.0 mm/min

3 结论

(1) GH3625合金宏观应力-应变曲线包括弹性变形阶段(σ ≤ 300 MPa),弹-塑性转变阶段(300 MPa < σ ≤ 350 MPa)和塑性变形阶段(σ > 350 MPa),这与细观晶格应变行为一致；同时,合金特定(hkl)晶面反射的晶格应变、峰宽和强度的演变表明变形速率对晶体弹性各向异性影响较小,而对晶体塑性各向异性影响较大。

(2) 随变形速率的增加,大角度晶界逐渐向小角度晶界转变,孪晶界的比例逐渐减小,晶粒由均匀变形向不均匀变形转变。

(3) 随变形速率的增加,{001}面上部分晶粒发生转动后重新取向形成Rotated-Cube织构{001}<110>,而{110}面上部分晶粒通过位错滑移后重新取向形成Goss织构{110}<001>；同时,{110}面上部分晶粒保留Rotated-Goss织构{110}<110>；此外,{111}面上部分晶粒发生转动后Brass-R织构{111}<112>消失,仅保留Brass-R织构{111}<110>。

(4) 随变形速率的增加,合金的ρ先减小后增加,而ρGND单调递增,ρSSD单调递减；同时,r = 0.2 mm/min时试样表现出反常的加工硬化行为,这归因于均匀变形产生的SSD对加工硬化做出了额外的贡献；此外,位错强化贡献和TEM观察证实了GH3625合金的塑性变形机制以位错滑移为主,其加工硬化机制是位错强化。