分享：基于纳米压痕逆算法的热冲压马氏体/贝氏体双相组织的微观力学性能

朱彬, 杨兰, 刘勇,, 张宜生

基于节能减排的重大需求，汽车轻量化得到了普遍的重视[1~3]。汽车轻量化需要在保证安全性的前提下进行，为此高强度钢热冲压零件在汽车中的应用越来越多[4~6]。传统热冲压工艺得到的完全马氏体零件，强度高但延伸率低，不能很好满足汽车碰撞中吸收能量的安全性要求[7]。近年来，研究发现，采用变强度热冲压工艺(tailored tempering properties，TTP)能够让高强度钢零件在不同的区域获得不同的力学性能[8~11]，可以更好地满足汽车安全性需求[12]。TTP工艺得到的零件上具有显著不同力学性能的区域之间存在过渡区域，过渡区域微观组织由多相组成，而微观组织的不同直接影响零件的宏观力学性能，故过渡区宏观力学性能不均匀，存在渐变的特性。零件的宏观力学性能一般通过拉伸实验和硬度测试等方法获得，只能代表材料的整体属性而无法用来评估材料局部微观组织的力学性能。此外，TTP工艺中的过渡区由于区域小，力学性能渐变，故难以通过拉伸实验来测定部分力学性能(如屈服强度等)。一般只能通过硬度测试估计过渡区的强度；本文作者[6]依据磁致巴克豪森效应(magnetic Barkhausen noise)进行无损检测来测试过渡区的力学性能，但该方法需要事先标定。因此有必要借助现代测试分析技术及算法分析，深入研究高强度钢热冲压后零件的微观组织对其微观力学性能的影响。

纳米压痕技术是一种高精度的检测技术，最早由Oliver和Pharr[13]提出并发展，目前已成为一种在微/纳米等尺度上评价材料局部性能的有效工具，该技术在研究陶瓷、玻璃、水泥浆和金属等多种材料的力学性能方面提供了有价值以及可靠的结果[14~18]。由于纳米压痕仪具有微牛顿级载荷量和纳米级位移进给量，因此可以准确地反应材料在微小载荷作用下，局部组织的载荷力与压痕深度之间的关系，为深入研究高强度钢热冲压后的微观组织及其力学性能之间的联系提供了可能。

本工作首先通过控制热冲压时的模具温度和保压时间获得包含全马氏体、全贝氏体以及马氏体/贝氏体混合组织的试件，然后通过纳米压痕实验获得马氏体/贝氏体混合组织零件不同微观区域的载荷-位移曲线，并利用纳米压痕逆算法[19]反求得到各微观组织的Young's模量、屈服强度等力学性能，进而推导出不同组织的本构模型，最后结合ABAQUS有限元数值模拟纳米压痕过程验证所构建本构模型的合理性和准确性，对探究高强度钢热冲压后微观组织与微观力学性能的关系具有重要意义。

1 实验材料与方法

1.1 实验材料

实验所用材料为1.2 mm厚汽车用热冲压高强钢，其主要化学成分(质量分数，%)为：C 0.216，Si 0.093，Mn1.2，Al 0.039，B 0.0023，P 0.0094，S ≤ 0.005，Fe余量。板料初始状态的微观组织为珠光体/铁素体，密度为7800 kg/m3，抗拉强度为400 MPa，延伸率为22%。

1.2 热冲压实验

热冲压实验在一套包含加热装置的平模系统上进行。该系统包含一台可调节保压时间的2000 kN高精度伺服压力机，尺寸为300 mm × 220 mm × 90 mm的平模，以及放置于模具内部的加热棒和加热控制装置。实验过程中在板料上焊接K型热电偶，测定板料从出炉到保压完毕后的温度变化，并结合之前工作中测定的本实验高强钢的连续冷却转变(continuous cooling transformation，CCT)曲线[20]分析板料的冷却曲线，预测其微观组织。实验过程如图1所示，首先将板料放入温度为930℃的加热炉中，加热并保温5 min使其完全奥氏体化，然后将板料快速转移至模具上，压力机下行闭合模具并保持压力一段时间(保压)后，压力机上行，取出板料。该过程中，板料分别在冷模具保压30 s、400℃模温下保压30 s、450℃模温下保压240 s，以获得不同成分比例的马氏体/贝氏体混合组织。

图1

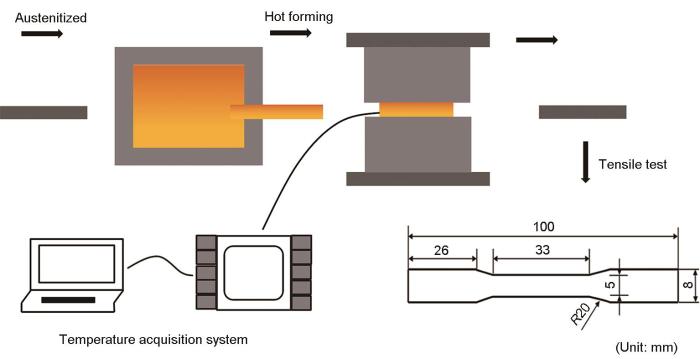
图1   实验流程示意图

Fig.1   Schematic of the experiment process

在3组热冲压工艺条件下得到的试件上取样，研磨抛光，在体积比为3%的硝酸酒精溶液中进行腐蚀，通过AURIGA扫描电镜(SEM)观察显微组织。通过CCT曲线对板料的冷却曲线进行分析，结合观察到的微观组织确定不同工艺条件下试件的相组成。除此之外，对不同实验组的试件制取拉伸试样(尺寸形状见图1)后在AG-IC100 kN材料力学性能试验机上进行拉伸实验，记录拉伸时的应力-应变，并通过引伸计实时测定记录延伸率，获得不同试样的应力-应变曲线。

1.3 纳米压痕实验

实验所用的纳米压痕设备为TI750型纳米压痕仪，Berkovich压头。对模温400℃、保压30 s工艺条件下制得的热冲压零件进行制样测试。测试前将待测样品研磨抛光以去除表面氧化层，同时保证试样平整，表面倾斜度不大于1°，以免产生错误的压痕数据。最后将试样用体积比为1∶7的高氯酸-酒精溶液电解抛光，保证测试结果不受表面氧化层和应力层的影响。实验过程中，固定压入深度为200 nm；为了分析试样不同微观组织区域的力学性能，设定6 × 6的点阵压痕并对压痕点进行编号，压痕点阵横纵间距定为30 μm × 30 μm，以避免相邻压痕之间的影响[21]。实验后配合组织观察以确定不同压痕点区域的微观组织。

2 实验结果与讨论

2.1 热冲压实验结果

图2为板料在不同模具温度与保压时间条件下的冷却曲线，其中黑色实线为本实验高强钢材料的CCT曲线，A代表奥氏体，F代表铁素体，P代表珠光体，B代表贝氏体，M代表马氏体，Ms和Mf分别为马氏体转变开始和终了温度。可以看出，在冷模具保压30 s工艺条件下，冷却曲线以较快的冷却速率穿过马氏体区域，而未穿过其他相区，因此判断该种工艺条件下得到完全马氏体组织(忽略少量的残余奥氏体，下同)；而对于模温400℃、保压30 s实验条件下的板料，冷却曲线穿过马氏体和贝氏体2个相转变区，因此得到马氏体/贝氏体混合组织；模温450℃、保压240 s工艺条件下，可以看到板料的冷却曲线完全穿过贝氏体区域，贝氏体转变完全，无马氏体生成，则该实验条件下得到完全贝氏体组织。

图2

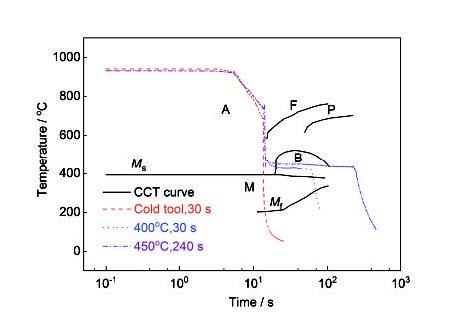
图2   不同模具温度和保压时间条件下试样的冷却曲线

Fig.2   Cooling curves of the samples under different tools temperatures and holding time during stamping (A: austenite, B: bainite, F: ferrite, P: pearlite; M—martensite, Ms: martensite transformation starting temperature, Mf: martensite transformation finishing temperature, CCT—continuous cooling transformation)

图3所示为3种热冲压工艺条件下试样微观组织的SEM像。在冷模具保压30 s条件下(图3a)，其微观组织为完全马氏体。模温400℃、保压30 s热冲压条件下得到的组织，同时有马氏体和贝氏体的存在(图3b)，马氏体的板条相对于图3a变得更加细小而分散，且贝氏体为板条状大致平行排列的下贝氏体组织。图3c为模温450℃、保压240 s条件下零件的微观组织，由于模温的增加和保压时间的延长，奥氏体完全转变为下贝氏体组织。

图3

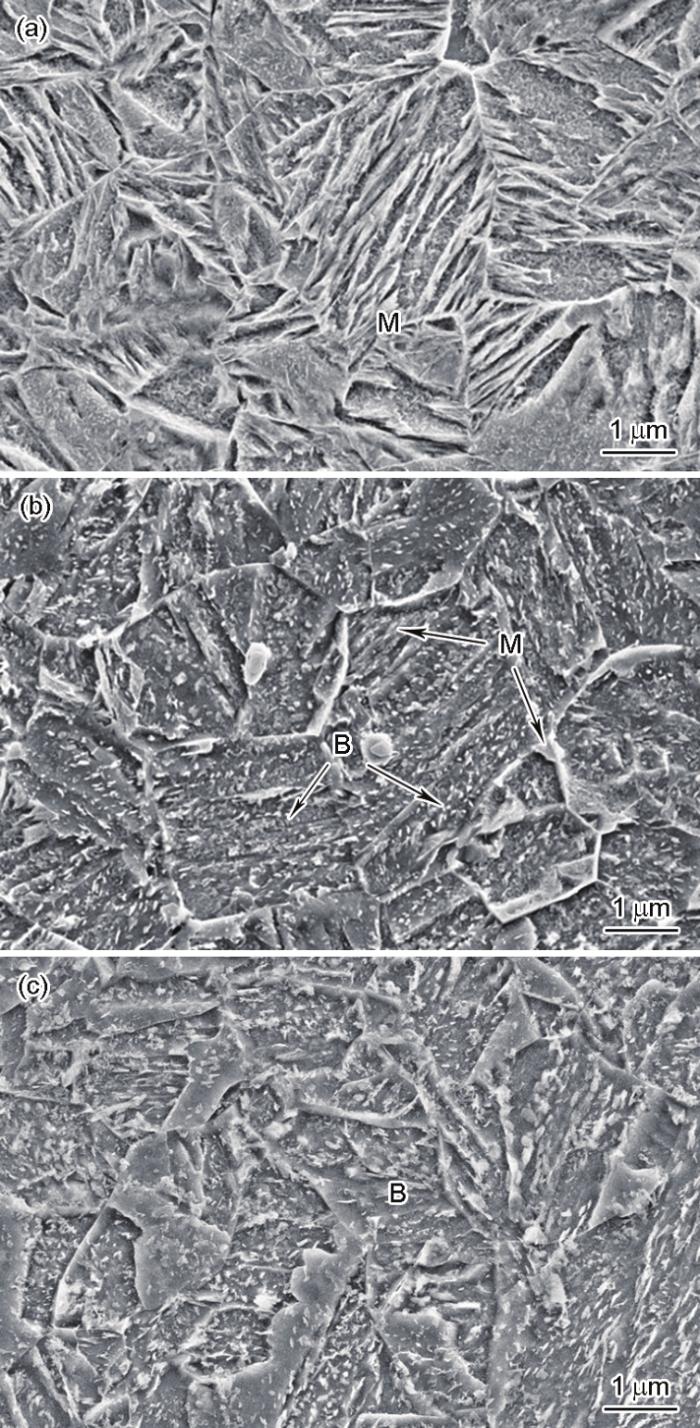
图3   不同模具温度和保压时间条件下试样微观组织的SEM像

(a) cold tool, 30 s

(b) 400oC, 30 s

(c) 450oC, 240 s

Fig.3   SEM images of microstructures of the samples under different tools temperatures and holding time during stamping

结合以上CCT曲线与显微组织观察，表明冷模具保压30 s、400℃模温下保压30 s、450℃模温下保压240 s条件下分别获得全马氏体、马氏体/贝氏体混合组织以及全贝氏体组织试件。

2.2 纳米压痕实验结果

对纳米压痕实验中部分代表性的压痕点进行分析，为方便描述，采用数字1、2、3对其进行编号，其中1号压痕打在贝氏体区域，2号压痕打在马氏体晶界附近且完全落在马氏体晶粒上，而3号压痕打在马氏体贝氏体混合区域。图4所示分别为1~3号压痕点的载荷-位移曲线。相同压痕深度(200 nm)条件下，1号压痕点所需载荷最小，2号压痕点所需载荷最大，而3号压痕点载荷介于两者之间。3个压痕点的显微硬度分别为3.76、6.69和4.95 GPa，与载荷大小变化一致。

图4

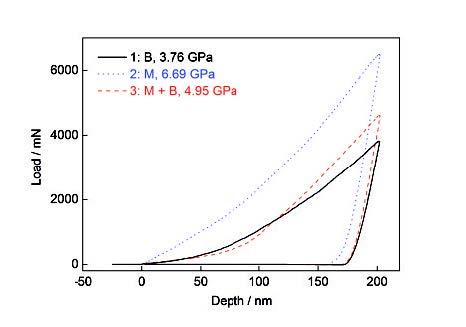
图4   3个代表性纳米压痕点(1~3号)的载荷-位移曲线

Fig.4   Load-displacement curves of the three representative nanoindentation points (Nos.1-3)

1~3号压痕点显微组织的SEM像如图5所示，可见，其验证了纳米压痕实验测得的硬度变化。

图5

图5   3个压痕点显微组织的SEM像

(a) No.1 (b) No.2 (c) No.3

Fig.5   SEM images of microstructures of different nanoindentation points

3 纳米压痕逆算法原理

3.1 纳米压痕基本原理

纳米压痕技术的基本原理是将测试压头作用在微/纳米尺度的小体积内，从而提取材料的力学响应，并根据获得的加载和卸载响应曲线(即载荷-位移曲线)在微/纳米尺度上研究材料的力学性能[22]。纳米压痕过程可以分为加载和卸载2个阶段：① 加载阶段当测试压头施加在材料表面的载荷足够小时，材料首先发生弹性变形；随着施加载荷的增大，弹性变形最大的区域产生塑性变形；当载荷足够大时，压入区域进入完全塑性阶段。② 在卸载阶段，随着压头的退出，先前压头压入区域的材料发生弹性恢复，而由于塑性变形产生的残余压痕则保留下来[23]。典型的载荷-位移曲线如图6所示。

图6

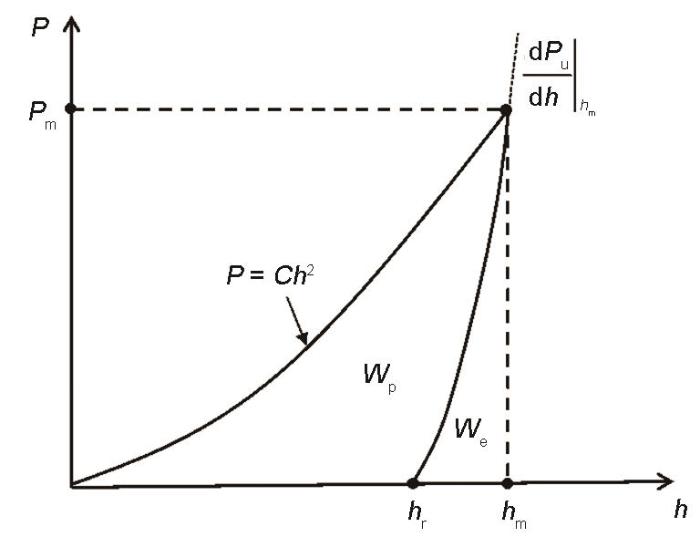
图6   纳米压痕实验获得的载荷-位移曲线

Fig.6   Load-displacement curve of the nanoindentation test (h—depth,P—load,hm—maximum indentation depth, Pm—maximum load, hr—residual indentation depth, C—loading curvature, Wp—plastic work, We—elastic work, Pu—unloading force, ${\left.\frac{\mathrm{d}{?}_{\mathrm{u}}}{\mathrm{d}?}\right|}_{{?}_{\mathrm{m}}}$—initial unloading slope)

纳米压痕逆算法的主要思想是利用纳米压痕实验获得的材料载荷-位移曲线进行逆向分析计算，从而获得材料的Young's模量、屈服强度等材料力学性能信息，最终获得材料完整的本构关系。显然，纳米压痕的应力施载方式与宏观拉伸的应力施载方式不尽相同，但本工作仅用于数值反算，提供一种用于获取TTP工艺中过渡区局部力学性能的方式。

图6中横坐标h为压痕深度，纵坐标P为载荷；hm为最大压深，Pm为加载过程中最大压深对应的载荷；hr为卸载结束后的残余压深；初始卸载斜率定义为${\left.\frac{\mathrm{d}{?}_{\mathrm{u}}}{\mathrm{d}?}\right|}_{{?}_{\mathrm{m}}}$，其中Pu为卸载力；Wt为加载过程中载荷P所做的总功，We为卸载过程中能够释放的弹性功，则储存的塑性功Wp= Wt- We。

加载过程中P与h可用Kick定律描述为[24]：

式中，C为与压入深度无关的材料常数，称为加载曲率。

将接触压力pave定义为[19]：

式中，Am是在施加载荷为最大值Pm时对应的压头真实投影面积。

在纳米压痕实验中，认定热冲压后的高强钢与大部分金属及合金一样，满足如下的本构关系[24]：

式中，E为压痕试样的弹性模量；R为强度系数；n为应变硬化指数；${?}_{\mathrm{y}}$为初始屈服强度，${?}_{\mathrm{y}}$为对应的屈服应变；$?$为总有效应变，其包括屈服应变${?}_{\mathrm{y}}$与有效塑性应变${?}_{\mathrm{p}}$ 2部分，即：

3.2 量纲分析法

量纲分析是一种基于物理现象发展数学模型的有力工具，在Dao等[19]提出的纳米压痕逆算法中，使用了一系列无量纲函数${\mathrm{\Pi }}_{\mathrm{1}}$、${\mathrm{\Pi }}_{\mathrm{2}}$、${\mathrm{\Pi }}_{\mathrm{3}}$、${\mathrm{\Pi }}_{\mathrm{4}}$、${\mathrm{\Pi }}_{\mathrm{5}}$及${\mathrm{\Pi }}_{\mathrm{6}}$，建立起压痕P-h曲线中各参量之间的无量纲函数之间的关系，进而反求得到被压材料的本构关系。

对于本构关系满足式(3)的材料，采用Berkovich压头进行压痕加载过程中P由材料的力学性能参数包括屈服强度、Young's模量、Poisson比、应变硬化指数、测试压头的力学性能以及压头压入深度等共同决定，可以表示为：

式中，${?}_{\mathrm{i}}$为压头的弹性模量，$?$和${?}_{\mathrm{i}}$分别为压痕试样和压头的Poisson比。对于本实验中的金刚石压头，分别取定${?}_{\mathrm{i}}$ = 1100 GPa，${?}_{\mathrm{i}}$ = 0.07[17]。对于高强钢材料，$?$给定0.27。则式(5)可通过折合弹性模量${?}^{\mathrm{*}}$简化为[19]：

其中，

同时定义代表性应变${?}_{\mathrm{r}}={?}_{\mathrm{p}}$来描述材料的塑性性能，并取${?}_{\mathrm{r}}$ = 0.033[19]，P可以另外表示为：

式(8)和(9)中的${?}_{\mathrm{r}}$为代表性应变${?}_{\mathrm{r}}$对应的应力。

采用量纲分析的$\mathrm{\Pi }$定理[19]，式(9)可以表示为[19]：

同时结合式(1)中压头压入载荷与位移的关系有[19]：

对于卸载过程，载荷Pu的函数除有$?$、$?$、$?$、${?}_{\mathrm{i}}$、${?}_{\mathrm{i}}$、${?}_{\mathrm{y}}$、$?$这7个变量之外，还与最大压深有关，则对于卸载斜率为[24]：

当h = hm时，由量纲分析得到[24]：

则Pu可以表示为[24]：

完全卸载后，Pu= 0，h = hr，整理得：

同理，可得到无量纲函数${\mathrm{\Pi }}_{\mathrm{4}}$及${\mathrm{\Pi }}_{\mathrm{5}}$[19]：

根据King[25]的工作，得到无量纲函数${\mathrm{\Pi }}_{\mathrm{6}}$：

式中，${?}^{*}$是一个与压头几何形状相关的常数，对于本实验中使用的Berkovich压头，取${?}^{*}$ = 1.2370[19]。

根据这些无量纲函数式，可以通过纳米压痕P-h曲线来反求得到被测材料的弹塑性性能。文中无量纲函数的具体解析表达式参见文献[19]。

3.3 逆算法结果

通过纳米压痕逆算法可以得到上文讨论的3个压痕点的E、${?}_{\mathrm{y}}$以及n等微观力学性能参数，如表1所示。利用上述3个参数，将拉伸实验中的应变代入式(3)，即可得到不同压痕点位置材料的应力-应变曲线。图7所示分别为模温400℃、保压30 s热冲压试件的宏观应力-应变曲线以及在该工艺条件下通过逆算法计算得到的3个压痕点处的应力-应变曲线。

表1   逆算法计算结果

Table 1  The results of the inverse analysis algorithms

新窗口打开| 下载CSV

图7

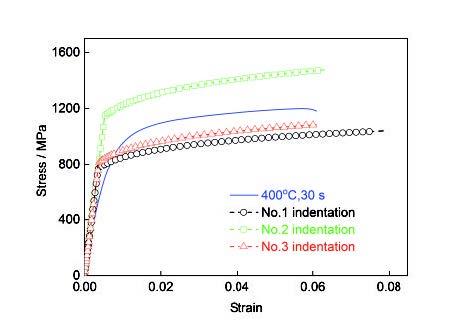
图7   模温400℃、保压30 s试件的应力-应变曲线及该条件下逆算法计算的3个压痕处的应力-应变曲线

Fig.7   Stress-strain curves of the specimen (400oC, 30 s) and three different indentation points calculated by the inverse algorithms in nanoindentation under the same process conditions

为了验证逆算法在微观组织力学性能计算的准确性，将热冲压实验中获得的全马氏体(冷模具保压30 s)和全贝氏体(模温450℃、保压240 s)试样通过拉伸实验得到的应力-应变曲线同全马氏体(2号压痕)和全贝氏体(1号压痕)的压痕处逆算法获得的应力-应变曲线进行对比，如图8所示。由图可知，全马氏体和全贝氏体试样的屈服强度分别为1160.3和745.0 MPa，则逆算法求得的马氏体、贝氏体屈服强度与拉伸实验获得数值的误差分别为-1.15%和3.38%。从图中可以看到，通过逆算法计算得到的1号压痕与2号压痕应力-应变曲线与热冲压后实验用钢对应组织试件的宏观应力-应变曲线吻合度较好，从而验证了逆算法计算的合理性和准确性。

图8

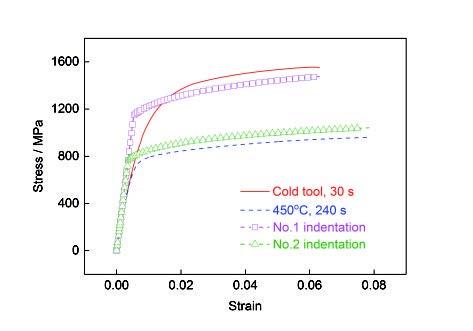
图8   全马氏体、全贝氏体试样应力-应变曲线与纳米压痕逆算法获得的同组织应力-应变曲线

Fig.8   Stress-strain curves of full martensite (cold tool, 30 s) and full bainite (450oC, 240 s) specimens, and the stress-strain curves of the same structures obtained by the inverse algorithms in nanoindentation

而进一步观察发现，纳米压痕实验中的2号压痕处通过逆算法得到的屈服强度比冷模具、保压30 s条件下得到的全马氏体组织试样通过拉伸实验获得的屈服强度小，可能原因是压痕实验的试样在400℃下保温30 s及取出模具后的一段时间内，快速形成的马氏体存在一个短暂的回火过程，此时马氏体硬度降低，则其强度相应下降。类似地，1号压痕处逆算法得到的屈服强度比模温450℃、保压240 s工艺条件下得到的全贝氏体组织试样通过拉伸实验获得的屈服强度大，可能原因是压痕实验的试样形成贝氏体的温度较低，保温时间较短，贝氏体中的铁素体碳的过饱和度更高，铁素体也比较细小，贝氏体中的碳化物也更细小弥散，导致贝氏体强度升高，于是屈服强度提升。除此之外，纳米压痕实验本身仅代表某一点处微观组织的力学性能，这与具有同样组织的零件的宏观力学性能具有一定的差异；同时，逆算法本身存在近似过程，也会带来误差。因此，各种综合因素导致了图7中产生的差异。显然，不同工艺方法得到的马氏体和贝氏体存在成分、尺寸及亚结构的差异，则其性能也会存在一定差异。本工作旨在通过纳米压痕实验及其逆算法提供一种用于获取TTP工艺中过渡区局部力学性能的方式，但复相组织不能通过拉伸实验获得其中马氏体和贝氏体组织各自的力学性能，需要通过全马氏体和全贝氏体组织试样拉伸实验获得。因此，本工作采用全马氏体和全贝氏体试样代替马氏体/贝氏体复相组织中对应的单相组织来进行宏观力学性能对比，验证该方法的准确性。

可以明显看到，试件的宏观力学性能与其不同实验点处的微观力学性能有明显差别(图7)，试件通过宏观拉伸实验计算得到的屈服强度为923.7 MPa，而逆算法求得的3个压痕处的屈服强度分别为770.2、1147.0和814.9 MPa，与宏观拉伸实验得到的屈服强度之间的差异分别为-16.62%、24.17%以及-11.78%。这说明仅仅通过拉伸实验得到热冲压材料的宏观力学性能是不够可靠的；反过来，对于具有多相组织的试件，基于部分区域的微观反算结果也并不能很好地代表其宏观力学性能，这也是产生上述差异的原因。上述3个压痕点通过逆算法求得的屈服强度的平均值为910.7 MPa，与实际拉伸实验结果923.7 MPa仅相差-1.41%。由此可见，可以采用多次基于微观反算的方法减少与宏观拉伸实验测试结果的差异。如果需要获取微小局部材料力学性能时，如TPP工艺中产生的过渡区，其力学性能具有渐变的特性，采用基于微观的逆算法反而更能代表该试样或该区域不同地方的力学性能。因此，无论是想获取整体还是微小局部材料的力学性能，本工作中基于纳米压痕逆算法得到材料力学性能的方法都是可取的，尤其是对于微观组织非均匀分布而需要获取局部材料性能的情况更有意义。

如上所述，考虑到块体材料成分或组织等存在诸多非均匀性的因素，对这种类型的块体材料(如本文中M + B的复合微观组织)进行纳米压痕检测时，测量数据不可避免地会存在一些差异性及离散性，比如位于不同区域的同一组织(单相或者多相)的测量数据会存在差异。因此本工作中对某一区域单个压痕点采用逆算法求得的相关材料参数仅代表该点处的材料性能，这对评估力学性能存在渐变特性区域的局部力学性能具有较高的应用价值，但却不能科学完整地表述其他情况时的材料性能。纳米压痕逆算法在本质上为针对某一单个压痕点材料参数的计算方法，因此，理论上可通过多次压痕实验获得多个压痕点数据，并进行相应的逆算法求解来降低这种差异性及离散性。为了减少工作量，作者认为也可根据同一组织不同区域压痕点的位移-载荷曲线分别获得其C、hm等参数，并在求得参数平均值后代入逆算法进行后续计算。但上述2种方法需要采用微观组织图像检测来筛选出同一组织的压痕点，工作量较大，因此需要在逆算法建模过程中考虑到这种差异性。

4 纳米压痕有限元模拟

4.1 有限元模型的建立

纳米压痕是一种非常局部的测试方法，由Saint-Venant原理[26]可知，被测材料的应力、应变只集中在压痕附近的区域，而远离压痕处的应力和应变为零，因此取被测材料的局部作为仿真中的压痕试件可提高计算效率。建立的有限元模型如图9所示，共有2个材料模型，即标准Berkovich压头和被测材料。压头形状[27]为三棱锥形，棱面与中心线的夹角为65.3°，棱边与中心线夹角77.05°。压头材质为金刚石，其硬度远高于被测材料，因此将其设置为理想刚体，可将整个刚体的力和位移集中到刚体的顶端，这一点指定为参考点。被测材料设定为10 µm × 10 µm × 2.5 µm的长方体，为均匀、各向同性的材料，材料的性能参数分别取逆算法计算得到的3个压痕位置的弹性和塑性参数。

图9

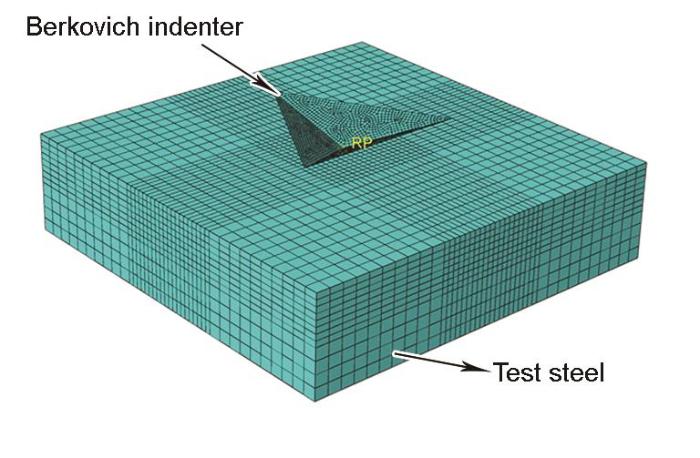
图9   纳米压痕仿真模型

Fig.9   Finite model of nanoindentation

实验过程中压头加载的深度很小且时间很长，因此可以将加载和卸载的过程看成是准静态过程。在加载的过程中，规定压头的运动方向只沿着压头中心线方向，最大压入深度为200 nm，；被测材料的底面约束所有的自由度。在卸载的过程中，规定压头运动方向同加载过程相反，卸载速率与加载速率相同，其余约束条件不变。纳米压痕过程中压头与被测材料之间为表面与表面接触，摩擦系数为0.1。模型网格单元类型为八节点线性六面体缩减积分单元。由于材料变形仅发生在压头附近，为减小计算时间和提高计算精度，靠近压头区域网格密度大，远离压头区域网格密度小[28](图9)，总单元数为19200。

4.2 有限元模拟结果分析

通过有限元模拟可以得到每个载荷步下的应力场等结果。图10为加载卸载过程中被测材料上表面的Mises应力云图。可以看出，随着压头压入的深度增大，被测材料的表面形貌发生了变形。在加载初期，应力较小，随着压头压入深度的增大，应力也随之增大。当压头压入深度达到最大时，材料的应力达到最大，为1500 MPa，最大应力出现在压痕顶尖处，且应力以压头的顶尖为圆心，沿着径向逐渐减小。图10c为完全卸载后的应力云图，最大应力出现位置与压深最大时不同，其最大值出现在压头棱边所留下的压痕处，而压头顶尖处附近的应力相对较小，说明该处的材料有很大的弹性恢复。

图10

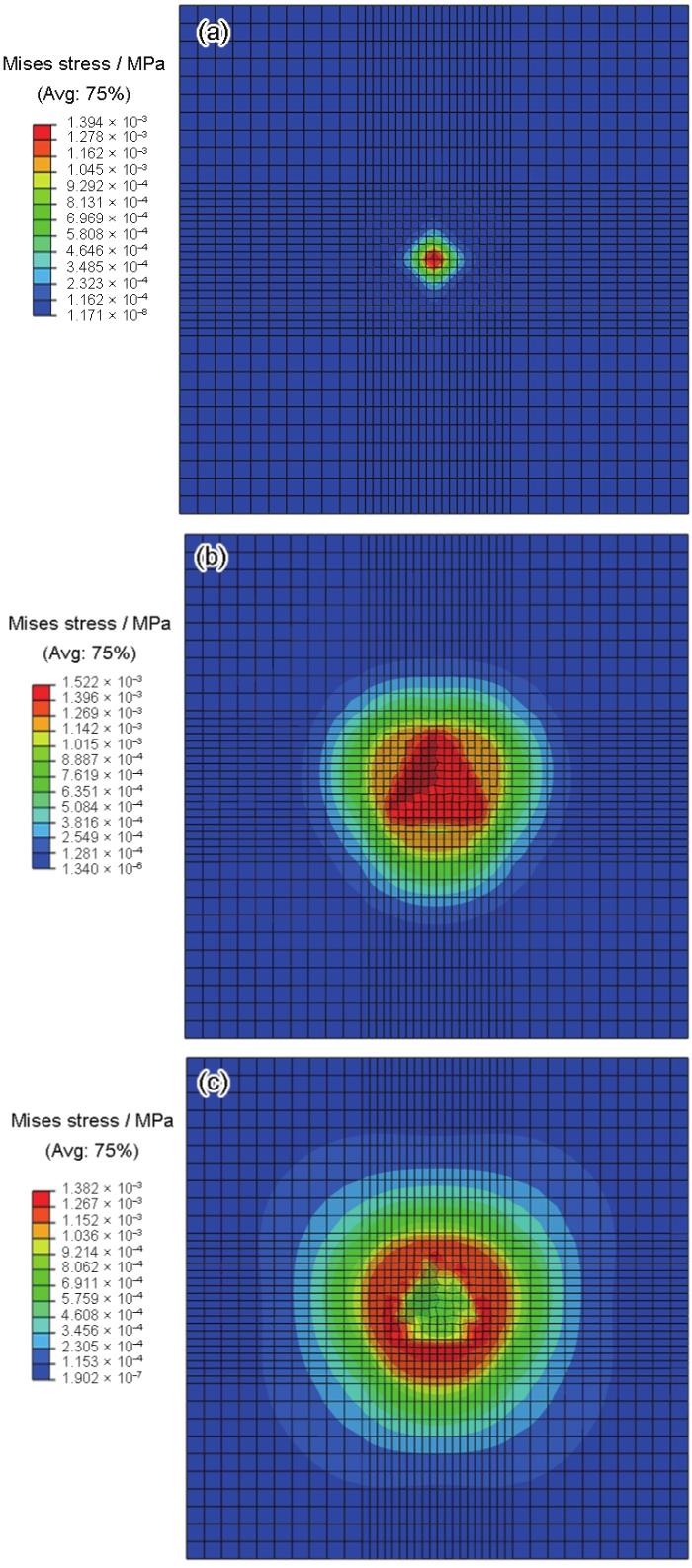
图10   模拟过程中应力分布图

(a) start loading

(b) maximum loading

(c) completely unloading

Fig.10   Stress distributions in simulation

不同压痕位置的实验载荷-位移曲线与对应的仿真载荷-位移曲线对比如图11所示。压痕模拟所得曲线与实验基本一致，最大压痕深度时对应的最大载荷也与实验基本符合，这进一步验证了逆算法的准确性。且完全卸载后材料的压入深度并未恢复到加载前材料没有变化的形态，说明材料发生了残余变形，体现了材料的塑性变形，与实际实验过程一致。

图11

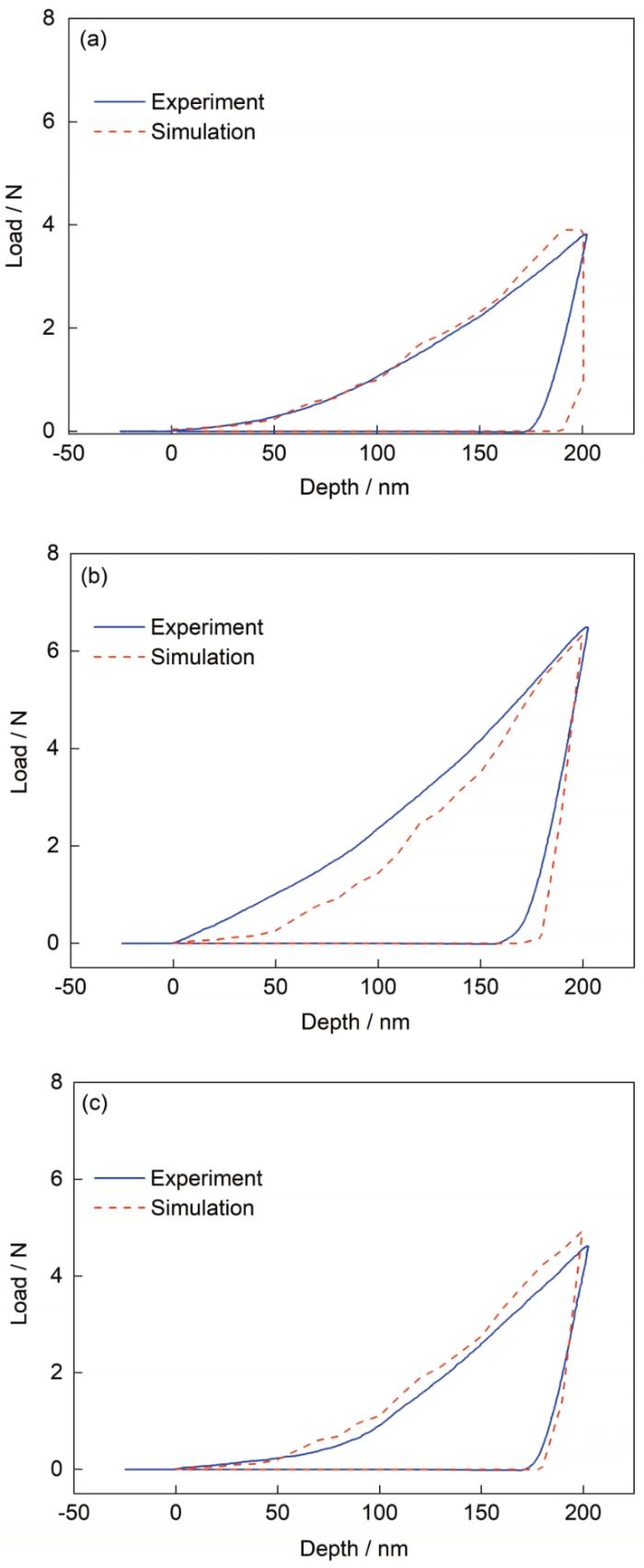
图11   不同压痕点位置的载荷-位移曲线

(a) No.1 (b) No.2 (c) No.3

Fig.11   Load-displacement curves in tests and simulations at different indentation points

5 结论

(1) 通过热冲压实验结合冷却曲线分析及组织观测，确定冷模具保压30 s、模温400℃保压30 s、模温450℃保压240 s 3种热冲压工艺条件下分别获得全马氏体组织、马氏体/贝氏体混合组织以及全贝氏体组织。

(2) 利用纳米压痕测试数据结合纳米压痕逆算法计算得到热冲压后实验用钢3处不同微观组织区域的微观力学性能，其中计算得到的全马氏体、全贝氏体组织屈服强度分别为1147.0和770.2 MPa，相较于拉伸实验求得的同组织的屈服强度误差分别为-1.15%和3.38%。

(3) 模温400℃保压30 s条件下纳米压痕逆算法求得3处不同微观组织的应力-应变曲线与拉伸实验获得的宏观应力-应变曲线具有一定的差异，其中屈服强度差异分别为16.62%、24.17%以及-11.78%，表明宏观条件下的力学性能同微观条件下的力学性能具有一定的差异；但同时3个点的屈服强度平均值与拉伸实验获得的值相差仅-1.41%。

(4) 通过纳米压痕有限元模拟得到3处压痕的载荷-位移曲线，与通过逆算法求得的对应载荷-位移曲线基本一致，验证了逆算法求得的材料微观力学性能的准确性。