分享：含有化合物相的共晶转变理论模型

许军锋,1,2, 张宝东1, Peter K Galenko2

共晶生长理论经历了漫长的发展过程。早在1946年，Zener[1]就注意到片层间距与生长速率有关，随后Hillert[2]严格分析液-固转变的浓度场，得到了共晶转变的浓度变化定量解。Tiller用最小过冷度判据[3]取代最大生长速率判据得到了半经验的共晶转变模型。直到1966年，Jackson和Hunt[4]在前人理论基础上推导了共晶生长Jackson-Hunt (JH)模型。JH模型奠定了两相耦合生长理论的基础，其优点是给出简单的过冷度-生长速率-片层间距(ΔT-V-λ)表达式，即使不懂推导过程，也不影响其使用，且影响共晶生长的主要参数都在模型考虑之中，因而至今依然很受欢迎。

然而，JH模型是在生长速率较小、液相平均成分近似为共晶点成分、层片间距远小于溶质扩散距离的假设下，得到的溶质扩散方程的解析解[4]，计算结果与大Peclet数的实验数据还有一定偏差。于是，1968年Donaghey和Tiller[5]研究了从小Peclet数到大Peclet数更宽范围的情况，获得了适合更高生长速率的扩散方程解，建立了DT模型，由于需要复杂的数值计算，当时并未给出ΔT-V-λ表达式。1987年，Trivedi、Magnin和Kurz[6]为了获得高生长速率溶质扩散方程解，把相图形状按α、β两相溶质分配系数(kα、kβ)的大小近似为“雪茄型” (kα ? kβ)和“等溶质分配系数型” (kα= kβ)，在JH和DT理论基础上，建立了适用高速生长的TMK模型。TMK模型忽略了随生长速率增加溶质拖拽的影响，随后Kurz和Trivedi[7]考虑了此情况，改进了平衡分配系数和液相线斜率的表达式，获得了KT模型。由于TMK和KT模型都受限于2种特殊相图，2000年，Zheng等[8]在DT模型基础上考虑了更宽成分范围的情况，得出了适用于更一般相图的模型。2004年，Ludwig和Leibbrandt[9]进一步修正了TMK模型的Fourier系数，以使其能用于多种相图，由于模型中的Fourier系数需要复杂的迭代计算，难以推广应用，与此相比，经典TMK模型形式简洁，应用更广泛。Li和Zhou[10]在TMK理论基础上考虑了动力学和热力学过冷的影响，建立了适用于更高速率的共枝晶生长LZ模型。Gao[11]在此基础上融入了对流对凝固的影响。Li和Kuribayashi[12]在LZ模型基础上提出了大过冷条件下共晶两相非耦合生长的模型框架。Wei等[13]进一步给出了共晶重熔分数的计算方程。Liu等[14]研究了有第三组元时LZ模型的表达式。Wang等[15]给出了共晶转变中动力学过冷度更准确的关系。Dong等[16]在LZ模型基础上引入了局部非平衡界面动力学的影响。

基于TMK理论发展的高速共晶生长模型最大的问题是仅适用2类特殊相图，因此在生长速率不大的情况，JH理论尚可应用，且不受相图种类限制。Magnin和Trivedi[17]在JH理论基础上考虑了共晶两相密度差异，给出了描述非规则层片共晶的MT模型。Catalina等[18]采用先求Bn，再反推B0的Fourier系数确定方法，并参考MT模型框架给出了考虑密度影响的模型。随后孟广惠和林鑫[19]采用自由能最低原理得到了确定共晶两相分数的更准确方法，进而完善了包含密度差的共晶模型。Wang等[20]根据三相点平衡条件和热力学极值原理得到考虑接触角变化的模型。Galenko和Herlach[21]发现在高速生长中从有溶质扩散到无扩散转变的极限速率并非无限大，而是一个可测量的速率，在此基础上得到了高速生长下的溶质扩散偏微分方程解析解，随后Xu等[22,23]基于此解给出了新的共晶生长模型。尽管共晶理论模型发展已久，在合金体系中含有金属间化合物相时，利用上述已有共晶生长理论模型就可以求解，但对于非从事共晶理论研究的人员来说，准确把握模型适用条件较为困难，常会导致模型误用。常见的问题是如何确定共晶生长过程化合物相的平衡分配系数、Fourier系数，以及成分等，这在一定程度上限制了共晶理论的发展与应用。

本工作在经典JH模型的理论框架下，完整导出有化合物相参与的共晶生长模型，包括溶质扩散方程导出，偏微分方程求解和Fourier系数的确定等过程，进而获得含有化合物相生长时的模型处理通用方法，给出有化合物相参与的共晶生长理论可供直接使用的表达式。随后给出理论模型的使用步骤，同时也讨论化合物相浓度对共晶生长动力学的影响。

1 适用中低生长速率下的JH模型

对于起始和结束浓度为0和1的相图，如Pb-Sn合金，JH模型或其他模型都能直接应用[24]。然而有合金化物相参与的共晶转变大多数β相浓度远小于1，最常见的有2类：(1) 两相溶质分配系数kα≠ 0，kβ≠ 0，形如图1a类，如Al-Al2Cu合金和Mg-Al12Mg17合金相图；(2) kα = 0，kβ≠ 0，形如图1b类，如Ni-Ni3B、Fe-Fe2B、Co-Co3B合金相图等。对于这种相图最基本的参数有7个：共晶点浓度(CE)，化合物相浓度(CB)，共晶温度(TE)，固溶度(Csα、Csβ)，液相线斜率(mα、mβ)。从几何上看，根据这7个参数可以复现出一个理想共晶相图的点线面。下面将从Fick定律出发，结合这些参数，推导适用于中低生长速率下的共晶生长模型。

图1

图1   含有化合物相的相图示意图

(a) kα≠ 0, kβ≠ 0 (b) kα = 0, kβ≠ 0

Fig.1   Phase diagrams containing compound phases(TE is the eutectic equilibrium temperature; CE is the eutectic concentration; mα and mβ are theliquidus line slopes on α-phase and β-phase, respectively; Csα and ΔCsβ are the concentrations in the solid of α-phase and β-phase, respectively;ΔCα, ΔCβ are the concentration differences between phases α, β and eutectic point (TE, CE) respectively; ΔC0 is concentration differences between α phase and β phase; CB is right-hand-side concentration of phase diagrams; kα, kβare solute distribution coefficients of α phase and β phase, respectively)

1.1 凝固界面溶质扩散方程

由Fick第二定律可知，对于三维空间静止坐标中浓度变化[25]：

$\frac{\partial ?}{\partial ?}=?\left(\frac{{\partial }^{\mathrm{2}}?}{\partial {?}^{\mathrm{2}}}+\frac{{\partial }^{\mathrm{2}}?}{\partial {?}^{\mathrm{2}}}+\frac{{\partial }^{\mathrm{2}}?}{\partial {?}^{\mathrm{2}}}\right)$(1)

式中，C为液相成分，D为液相扩散系数，t为时间。对于层片共晶，横切面Y轴方向是平面，忽略Y轴浓度变化，所以式(1)变形为：

$\frac{{\partial }^{\mathrm{2}}?}{\partial {?}^{\mathrm{2}}}+\frac{{\partial }^{\mathrm{2}}?}{\partial {?}^{\mathrm{2}}}=\frac{\mathrm{1}}{?}\frac{\partial ?}{\partial ?}$(2)

以上方程为静止坐标(X, Z)的扩散方程。共晶生长过程，凝固界面是移动的，需要建立移动坐标系。假设凝固界面移动速率为V，则对于移动的坐标系(x, z)，如图2，在共晶生长方向上，界面位置为$?$ = $?-??$，则界面和成分随时间变化符合：

图2

图2   凝固界面的移动坐标系和静止坐标

Fig.2   The moving and the stationary coordinate systems of the solidified interface (Sα and Sβ represent the half of interlamellar spacing for each phase such that λ = 2(Sα + Sβ) is the lamellar spacing; V is the growth velocity; θα and θβ are the contact angles at the triple point junction)

$\frac{\partial ?}{\partial ?}=-?,\frac{\partial ?}{\partial ?}=\frac{\partial ?}{\partial ?}\frac{\partial ?}{\partial ?}=-?\frac{\partial ?}{\partial ?}$(3)

由于$\partial ?/\partial ?$ = 1，$\partial ?/\partial ?$ = 1，$\partial ?/\partial ?$ = $\partial ?/\partial ?$，$\partial ?/\partial ?$ = $\partial ?/\partial ?$，带入式(2)得：

$\frac{{\partial }^{\mathrm{2}}?}{\partial {?}^{\mathrm{2}}}+\frac{{\partial }^{\mathrm{2}}?}{\partial {?}^{\mathrm{2}}}=-\frac{?}{?}\frac{\partial ?}{\partial ?}$(4)

也即：

$\frac{{\partial }^{\mathrm{2}}?}{\partial {?}^{\mathrm{2}}}+\frac{{\partial }^{\mathrm{2}}?}{\partial {?}^{\mathrm{2}}}+\frac{?}{?}\frac{\partial ?}{\partial ?}=\mathrm{0}$(5)

从图2可知，上述溶质扩散方程的边界条件为：①周期条件：C(x + λ) = C(x) (在x方向)；②对称条件：$\partial ?/\partial ?$ = 0 (当x = 0和x = Sα + Sβ时)；③远场条件：$?={?}_{\mathrm{\infty }}={?}_{\mathrm{E}}+\mathrm{\Delta }{?}_{\mathrm{\infty }}$ (在z → ∞时)。其中，λ = 2(Sα+ Sβ)，Sα和Sβ分别为共晶α相和β相的半层厚，C∞为合金初始成分，ΔC∞为初始成分与共晶点的偏差。式(5)就是共晶生长界面移动过程的界面到液相区溶质扩散偏微分方程，反映了浓度在x方向(垂直共晶层片)和z方向(平行于共晶层片)的变化规律。

1.2 偏微分方程求解

对偏微分方程(5)求解，因为有x和z 2个变量，首先需要进行变量分离。偏微分方程的解一般由2部分构成：通解+特解。假设方程(5)的一个可能解为，C(x, z) = Ω(x, z) + C∞，在z = ∞时Ω(x, z)为0，C∞为z = ∞时远离界面位置的实际浓度，也就是合金的原始成分。为了变量分离，假设Ω(x, z)由2个独立函数变量构成：

$?(?,?)=?(?)?(?)$(6)

把式(6)带入式(5)得：

$\frac{{\mathrm{d}}^{\mathrm{2}}?}{\mathrm{d}{?}^{\mathrm{2}}}?+\frac{{\mathrm{d}}^{\mathrm{2}}?}{\mathrm{d}{?}^{\mathrm{2}}}?+\frac{?}{?}\frac{\mathrm{d}?}{\mathrm{d}?}=\mathrm{0}$(7)

两边同除以P·Q得：

$\frac{\mathrm{1}}{?}\frac{{\mathrm{d}}^{\mathrm{2}}?}{\mathrm{d}{?}^{\mathrm{2}}}+\frac{\mathrm{1}}{?}\frac{{\mathrm{d}}^{\mathrm{2}}?}{\mathrm{d}{?}^{\mathrm{2}}}+\frac{?}{?}\frac{\mathrm{1}}{?}\frac{\mathrm{d}?}{\mathrm{d}?}=\mathrm{0}$(8)

把含x和z的项分别整理，进而可得，

$-\frac{\mathrm{1}}{?}\frac{{\mathrm{d}}^{\mathrm{2}}?}{\mathrm{d}{?}^{\mathrm{2}}}=\frac{\mathrm{1}}{?}\frac{{\mathrm{d}}^{\mathrm{2}}?}{\mathrm{d}{?}^{\mathrm{2}}}+\frac{?}{?}\frac{\mathrm{1}}{?}\frac{\mathrm{d}?}{\mathrm{d}?}=?$(9)

这里，a为常数，符号为正。于是在x方向：

$\frac{\mathrm{1}}{?}\frac{{\mathrm{d}}^{\mathrm{2}}?}{\mathrm{d}{?}^{\mathrm{2}}}=-?$(10)

两边同乘以P整理得：

$\frac{{\mathrm{d}}^{\mathrm{2}}?}{\mathrm{d}{?}^{\mathrm{2}}}+??=\mathrm{0}$(11)

这类二阶常系数齐次线性微分方程的通解可写成：

$?(?)={?}_{\mathrm{1}}\mathrm{c}\mathrm{o}\mathrm{s}(\sqrt[]{?}?)+{?}_{\mathrm{2}}\mathrm{s}\mathrm{i}\mathrm{n}(\sqrt[]{?}?)$(12)

这里的P1、P2为通解的系数。在ｚ方向上有：

$\frac{\mathrm{1}}{?}\frac{{\mathrm{d}}^{\mathrm{2}}?}{\mathrm{d}{?}^{\mathrm{2}}}+\frac{?}{?}\frac{\mathrm{1}}{?}\frac{\mathrm{d}?}{\mathrm{d}?}=?$(13)

上式两边同乘以Q，整理得：

$\frac{{\mathrm{d}}^{\mathrm{2}}?}{\mathrm{d}{?}^{\mathrm{2}}}+\frac{?}{?}\frac{\mathrm{d}?}{\mathrm{d}?}-??=\mathrm{0}$(14)

解此二阶常系数齐次线性微分方程，得到通解为：

$?(?)={?}_{\mathrm{1}}\cdot \mathrm{e}\mathrm{x}\mathrm{p}\left\{\left[\frac{-?}{\mathrm{2}?}-\sqrt[]{{\left(\frac{?}{\mathrm{2}?}\right)}^{\mathrm{2}}+?}\right]?\right\}+$${?}_{\mathrm{2}}\cdot \mathrm{e}\mathrm{x}\mathrm{p}\left\{\left[\frac{-?}{\mathrm{2}?}+\sqrt[]{{\left(\frac{?}{\mathrm{2}?}\right)}^{\mathrm{2}}+?}\right]?\right\}$(15)

其中Q1和Q2为通解的系数。下面由边界条件确定2个通解的具体形式。对式(12)两边求导得：

$\frac{\mathrm{d}?(?)}{\mathrm{d}?}=-\sqrt[]{?}{?}_{\mathrm{1}}\mathrm{s}\mathrm{i}\mathrm{n}(\sqrt[]{?}?)+\sqrt[]{?}{?}_{\mathrm{2}}\mathrm{c}\mathrm{o}\mathrm{s}(\sqrt[]{?}?)$(16)

由对称边界条件，在x = 0时，$\partial ?$ / $\partial ?$= 0，于是式(16)变成0 = $\mathrm{0}+\sqrt[]{?}{?}_{\mathrm{2}}$，这说明P2 = ０，并且有：

$\frac{\mathrm{d}?(?)}{\mathrm{d}?}=-\sqrt[]{?}{?}_{\mathrm{1}}\mathrm{s}\mathrm{i}\mathrm{n}(\sqrt[]{?}?)$(17)

由对称边界条件，当x = ${?}_{?}+{?}_{?}$时，也有$\partial ?$ / $\partial ?$ = 0，说明0 = $-\sqrt[]{?}{?}_{\mathrm{1}}\mathrm{s}\mathrm{i}\mathrm{n}\left[\sqrt[]{?}({?}_{?}+{?}_{?})\right]$，显然${?}_{\mathrm{1}}\ne \mathrm{0}$，那么只有$\mathrm{s}\mathrm{i}\mathrm{n}\left[\sqrt[]{?}({?}_{?}+{?}_{?})\right]$ = 0，这样：$\sqrt[]{?}({?}_{?}+{?}_{?})$ = $?\mathrm{\pi }$ (n = 0, 1, 2, …)，所以有：

$?={\left(\frac{?\mathrm{\pi }}{{?}_{?}+{?}_{?}}\right)}^{\mathrm{2}}$(18)

将式(18)和P2 = 0带入式(12)可得：

$?(?)={?}_{\mathrm{1}}\mathrm{c}\mathrm{o}\mathrm{s}\left(\frac{?\mathrm{\pi }?}{{?}_{?}+{?}_{?}}\right)$(19)

将式(18)带入式(15)得：

$?(?)={?}_{\mathrm{1}}\cdot \mathrm{e}\mathrm{x}\mathrm{p}\left\{\left[\frac{-?}{\mathrm{2}?}-\sqrt[]{{(\frac{?}{\mathrm{2}?})}^{\mathrm{2}}+{\left(\frac{?\mathrm{\pi }}{{?}_{?}+{?}_{?}}\right)}^{\mathrm{2}}}\right]?\right\}+$${?}_{\mathrm{2}}\cdot \mathrm{e}\mathrm{x}\mathrm{p}\left\{\left[\frac{-?}{\mathrm{2}?}+\sqrt[]{{(\frac{?}{\mathrm{2}?})}^{\mathrm{2}}+{\left(\frac{?\mathrm{\pi }}{{?}_{?}+{?}_{?}}\right)}^{\mathrm{2}}}\right]?\right\}$(20)

对于式(20)，当$?\to \mathrm{\infty }$时，${?}_{\mathrm{2}}\cdot \mathrm{e}\mathrm{x}\mathrm{p}\left\{\left[\frac{-?}{\mathrm{2}?}+\sqrt[]{{\left(\frac{?}{\mathrm{2}?}\right)}^{\mathrm{2}}+{\left(\frac{?\mathrm{\pi }}{{?}_{?}+{?}_{?}}\right)}^{\mathrm{2}}}\right]?\right\}$也趋于无穷大，但由于浓度的变化不会超出0~1范围，与无穷大矛盾，因而有${?}_{\mathrm{2}}$ = 0，于是式(15)变为：

$?(?)={?}_{\mathrm{1}}\cdot \mathrm{e}\mathrm{x}\mathrm{p}\left\{\left[\frac{-?}{\mathrm{2}?}-\sqrt[]{{\left(\frac{?}{\mathrm{2}?}\right)}^{\mathrm{2}}+{\left(\frac{?\mathrm{\pi }}{{?}_{?}+{?}_{?}}\right)}^{\mathrm{2}}}\right]?\right\}$(21)

带入式(6)会得到：

$?(?,?)=?(?)?(?)={?}_{\mathrm{1}}\mathrm{c}\mathrm{o}\mathrm{s}\left(\frac{?\mathrm{\pi }?}{{?}_{?}+{?}_{?}}\right)\cdot {?}_{\mathrm{1}}\cdot$$\mathrm{e}\mathrm{x}\mathrm{p}\left\{\left[\frac{-?}{\mathrm{2}?}-\sqrt[]{{\left(\frac{?}{\mathrm{2}?}\right)}^{\mathrm{2}}+{\left(\frac{?\mathrm{\pi }}{{?}_{?}+{?}_{?}}\right)}^{\mathrm{2}}}\right]?\right\}$(22)

将P1、Q1合并为Fourier系数Bn得：

$?(?,?)={\displaystyle \sum _{?=\mathrm{0}}^{\mathrm{\infty }}}{?}_{?}\mathrm{c}\mathrm{o}\mathrm{s}(\frac{?\mathrm{\pi }?}{{?}_{?}+{?}_{?}})\cdot \mathrm{e}\mathrm{x}\mathrm{p}(-{?}_{?}?)$(23)

这里，${?}_{?}=\left[\frac{?}{\mathrm{2}?}+\sqrt[]{{\left(\frac{?}{\mathrm{2}?}\right)}^{\mathrm{2}}+{\left(\frac{?\mathrm{\pi }}{{?}_{?}+{?}_{?}}\right)}^{\mathrm{2}}}\right]$。

由远场边界条件可知：当ｚ → ∞时，无论x为何值，C = C∞为一个特解，于是得到共晶生长界面前沿溶质浓度分布偏微分方程的一个解析解为[4]：

$?(?,?)={?}_{\mathrm{\infty }}+{\displaystyle \sum _{?=\mathrm{0}}^{\mathrm{\infty }}}{?}_{?}\mathrm{c}\mathrm{o}\mathrm{s}(\frac{?\mathrm{\pi }?}{{?}_{?}+{?}_{?}})\cdot \mathrm{e}\mathrm{x}\mathrm{p}(-{?}_{?}?)$(24a)

由于式(24a)最后一项在n = 0时形式简单，Fourier系数B0可以独立出来，浓度表达式可写成[4]：

$?(?,?)={?}_{\mathrm{\infty }}+{?}_{\mathrm{0}}\mathrm{e}\mathrm{x}\mathrm{p}(-\frac{?}{?}?)+$${\displaystyle \sum _{?=\mathrm{1}}^{\mathrm{\infty }}}{?}_{?}\mathrm{c}\mathrm{o}\mathrm{s}(\frac{?\mathrm{\pi }?}{{?}_{?}+{?}_{?}})\mathrm{e}\mathrm{x}\mathrm{p}(-{?}_{?}?)$(24b)

以上即为共晶凝固界面溶质浓度分布的解析表达式。可以看出，结构为Fourier级数形式，且系数B0、Bn待定。

1.3 Fourier系数B0和Bn的确定

在共晶生长模型中，B0和Bn的值需通过界面质量守恒的边界条件确定[4~11]。对于有化合物相参与的共晶生长过程，如图1a所示相图，右侧化合物相不处于整个相图最右端，其浓度不能按1对待，设为CB，于是按照界面溶质质量守恒定律[4~6]可以得到：

$-?{\left(\frac{\partial ?}{\partial ?}\right)}_{?=\mathrm{0}}=\left\{\begin{array}{l}??(?,\mathrm{0})\left(\mathrm{1}-{?}_{?}^{}\right)(?-\mathrm{p}\mathrm{h}\mathrm{a}\mathrm{s}\mathrm{e})\\ -?[??-?(?,\mathrm{0})]\left(\mathrm{1}-{?}_{?}^{}\right)(?-\mathrm{p}\mathrm{h}\mathrm{a}\mathrm{s}\mathrm{e})\end{array}\right.$(25)

这里，kα和kβ为共晶两相的溶质分配系数，$?(?,\mathrm{0})$表示界面(z = 0)处的溶质浓度。当图1a相图kβ = 0时或者Csβ= CB时，就变成图1b所示的相图情况，这时式(25)就变为图1b的溶质守恒方程，而且方程右边变得更简单。这类相图很常见，例如Fe-B、Ni-B、Co-B等合金。而当CB = 1时，式(25)变成了两端成分为0和1的不含化合物相情况。

由边界条件求解B0和Bn，需要对浓度方程(24b)两端求导，并带入式(25)：

$\frac{\partial ?}{\partial ?}=-\frac{?}{?}{?}_{\mathrm{0}}\mathrm{e}\mathrm{x}\mathrm{p}(-\frac{?}{?}?)-$${\displaystyle \sum _{?=\mathrm{1}}^{\mathrm{\infty }}}{?}_{?}{?}_{?}\mathrm{c}\mathrm{o}\mathrm{s}(\frac{\mathrm{2}?\mathrm{\pi }?}{?})\mathrm{e}\mathrm{x}\mathrm{p}(-{?}_{?}?)$(26)

为了方便表示，定义函数u(x)：

$?(?)=-?\frac{\partial ?}{\partial ?}\left|{}_{?=\mathrm{0}}\right.={?}_{\mathrm{0}}?+?{\displaystyle \sum _{?=\mathrm{1}}^{\mathrm{\infty }}}{?}_{?}{?}_{?}\mathrm{c}\mathrm{o}\mathrm{s}(\frac{\mathrm{2}?\mathrm{\pi }?}{?})$(27a)$?(?)=\left\{\begin{array}{l}??(?,\mathrm{0})(\mathrm{1}-{?}_{?})(?-\mathrm{p}\mathrm{h}\mathrm{a}\mathrm{s}\mathrm{e})\\ -?[??-?(?,\mathrm{0})](\mathrm{1}-{?}_{?})(?-\mathrm{p}\mathrm{h}\mathrm{a}\mathrm{s}\mathrm{e})\end{array}\right.$(27b)

于是对α相：

$??(?,\mathrm{0})(\mathrm{1}-{?}_{?})={?}_{\mathrm{0}}?+?{\displaystyle \sum _{?=\mathrm{1}}^{\mathrm{\infty }}}{?}_{?}{?}_{?}\mathrm{c}\mathrm{o}\mathrm{s}(\frac{\mathrm{2}?\mathrm{\pi }?}{?})$(28a)

对β相：

$-?[??-?(?,\mathrm{0})](\mathrm{1}-{?}_{?})=$${?}_{\mathrm{0}}?+?{\displaystyle \sum _{?=\mathrm{1}}^{\mathrm{\infty }}}{?}_{?}{?}_{?}\mathrm{c}\mathrm{o}\mathrm{s}(\frac{\mathrm{2}?\mathrm{\pi }?}{?})$(28b)

对式(28a)和(28b)两端分别在0~Sα和Sα~(Sα+ Sβ)区间对x积分后得到：

$??(?,\mathrm{0})\left(\mathrm{1}-{?}_{?}^{}\right){?}_{?}={?}_{\mathrm{0}}?{?}_{?}+?{\displaystyle \sum _{?=\mathrm{1}}^{\mathrm{\infty }}}{?}_{?}{?}_{?}\frac{\mathrm{s}\mathrm{i}\mathrm{n}(?\mathrm{\pi }{?}_{?})}{?\mathrm{\pi }}$(29a)$-?[??-?(?,\mathrm{0})]\left(\mathrm{1}-{?}_{?}^{}\right){?}_{?}=$${?}_{\mathrm{0}}?{?}_{?}-?{\displaystyle \sum _{?=\mathrm{1}}^{\mathrm{\infty }}}{?}_{?}{?}_{?}\frac{\mathrm{s}\mathrm{i}\mathrm{n}(?\mathrm{\pi }{?}_{?})}{?\mathrm{\pi }}$(29b)

这里fα= Sα /(Sα+ Sβ)，fβ= Sβ /(Sα+ Sβ)，分别为α和β相的分数。为了消去Bn，两式相加得：

$??(?,\mathrm{0})\left(\mathrm{1}-{?}_{?}^{}\right){?}_{?}-?[??-?(?,\mathrm{0})]\left(\mathrm{1}-{?}_{?}^{}\right){?}_{?}=$${?}_{\mathrm{0}}?({?}_{?}+{?}_{?})$(30)

于是可以解出B0：

${?}_{\mathrm{0}}=?(?,\mathrm{0})\left(\mathrm{1}-{?}_{?}^{}\right){?}_{?}-[??-?(?,\mathrm{0})]\left(\mathrm{1}-{?}_{?}^{}\right){?}_{?}$(31a)

在过冷度不大的情况下，可以认为液相浓度近似为共晶成分，C(x,0) = CE，kα和kβ的值为平衡相图上共晶温度的溶质分配系数，则式(31a)回到JH模型的表达式[4]：

${?}_{\mathrm{0}}=\mathrm{\Delta }{?}_{?}{?}_{?}-\mathrm{\Delta }{?}_{?}{?}_{?}$(31b)

这里值得注意，

$\mathrm{\Delta }{?}_{?}={?}_{\mathrm{E}}\left(\mathrm{1}-{?}_{?}^{}\right)={?}_{\mathrm{E}}-{?}_{\mathrm{s}?}$(31c)$\mathrm{\Delta }{?}_{?}=\left(\mathrm{1}-{?}_{?}^{}\right)(??-{?}_{\mathrm{E}})={?}_{\mathrm{s}?}-{?}_{\mathrm{E}}$(31d)

Csα和Csβ分别是α、β两相在共晶温度的固溶度，如图1a所示。如果过冷度较大，两相固溶度随生长速率的变化不可忽略，B0只能用式(31a)。

对Bn的求解，参考Fourier级数的系数公式和方程(27)可知：

$?{?}_{?}{?}_{?}=\frac{\mathrm{2}}{?/\mathrm{2}}{\int }_{\mathrm{0}}^{?/\mathrm{2}}?(?)\mathrm{c}\mathrm{o}\mathrm{s}(\frac{\mathrm{2}?\mathrm{\pi }?}{?})\mathrm{d}?=$$\frac{\mathrm{4}}{?}\left[??(?,\mathrm{0})\left(\mathrm{1}-{?}_{?}^{}\right){\int }_{\mathrm{0}}^{{?}_{?}?/\mathrm{2}}\mathrm{c}\mathrm{o}\mathrm{s}(\frac{\mathrm{2}?\mathrm{\pi }?}{?})\mathrm{d}?-?(??-?(?,\mathrm{0}))(\mathrm{1}-{?}_{?}^{}){\int }_{{?}_{?}?/\mathrm{2}}^{?/\mathrm{2}}\mathrm{c}\mathrm{o}\mathrm{s}(\frac{\mathrm{2}?\mathrm{\pi }?}{?})\mathrm{d}?\right]=$$\frac{\mathrm{4}}{?}\left[\frac{?}{\mathrm{2}?\mathrm{\pi }}?(\mathrm{1}-{?}_{?}^{})?(?,\mathrm{0})+\frac{?}{\mathrm{2}?\mathrm{\pi }}?\left(\mathrm{1}-{?}_{?}^{}\right)(??-?(?,\mathrm{0}))\right]\mathrm{s}\mathrm{i}\mathrm{n}(?\mathrm{\pi }{?}_{?})=$$\left[\frac{\mathrm{2}?(\mathrm{1}-{?}_{?}^{})?(?,\mathrm{0})}{?\mathrm{\pi }}+\frac{\mathrm{2}?(\mathrm{1}-{?}_{?}^{})(??-?(?,\mathrm{0}))}{?\mathrm{\pi }}\right]\mathrm{s}\mathrm{i}\mathrm{n}(?\mathrm{\pi }{?}_{?})=$$\frac{\mathrm{2}?}{?\mathrm{\pi }}\left[(\mathrm{1}-{?}_{?}^{})?(?,\mathrm{0})+(\mathrm{1}-{?}_{?}^{})(??-?(?,\mathrm{0}))\right]\mathrm{s}\mathrm{i}\mathrm{n}(?\mathrm{\pi }{?}_{?})$(32)

式(32)右端是把共晶界面0 ≤ x < Sα和Sα≤ x < Sα + Sβ两段区间(图2)先分开计算再合并到一起的过程。过冷度不大的情况，近似认为液相浓度C(x,0) = CE，于是移项整理可得：

${?}_{?}=\frac{\mathrm{2}?\mathrm{s}\mathrm{i}\mathrm{n}(?\mathrm{\pi }{?}_{?})}{??\mathrm{\pi }{?}_{?}}\left[(\mathrm{1}-{?}_{?}^{}){?}_{\mathrm{E}}+(\mathrm{1}-{?}_{?}^{})(??-{?}_{\mathrm{E}})\right]$(33a)

根据图1a分析，上式也可写成与JH模型完全相同的形式：

${?}_{?}=\frac{\mathrm{2}?\mathrm{s}\mathrm{i}\mathrm{n}(?\mathrm{\pi }{?}_{?})}{??\mathrm{\pi }{?}_{?}}(\mathrm{\Delta }{?}_{?}+\mathrm{\Delta }{?}_{?})$(33b)

但只有CB = 1，才得到两端成分为0和1的共晶相图的表达式。如果两相固溶度Csα和Csβ的差为ΔC0 = Csβ - Csα(图1a)，而且ΔCα+ΔCβ=ΔC0，则可得到Bn表达式：

${?}_{?}=\frac{\mathrm{2}?\mathrm{s}\mathrm{i}\mathrm{n}(?\mathrm{\pi }{?}_{?})}{??\mathrm{\pi }{?}_{?}}({?}_{\mathrm{s}?}-{?}_{\mathrm{s}\mathrm{\alpha }})=\frac{\mathrm{2}?\mathrm{s}\mathrm{i}\mathrm{n}(?\mathrm{\pi }{?}_{?})}{??\mathrm{\pi }{?}_{?}}\mathrm{\Delta }{?}_{\mathrm{0}}$(33c)

式(31b)和(33b)给出的B0和Bn表达式与JH模型[4]的表达式完全相同。若相图为等溶质分配系数型，即kα = kβ = ke，ke为平衡溶质分配系数，从方程(33a)可得：

${?}_{?}=\frac{\mathrm{2}?\mathrm{s}\mathrm{i}\mathrm{n}(?\mathrm{\pi }{?}_{?})}{??\mathrm{\pi }{?}_{?}}(\mathrm{1}-{?}_{\mathrm{e}})??$(33d)

从上式看化合物相对Bn影响显著。若共晶中化合物相无固溶度(kβ=0)，从图1b可知，ΔCα + ΔCβ = CB-Csα，于是有：

${?}_{?}=\frac{\mathrm{2}?\mathrm{s}\mathrm{i}\mathrm{n}(?\mathrm{\pi }{?}_{?})}{??\mathrm{\pi }{?}_{?}}(??-{?}_{\mathrm{s}\mathrm{\alpha }})$(33e)

若kα = kβ=0，即相图两端相都无固溶度，例如Mg-Mg2Cu合金相图，则有：

${?}_{?}=\frac{\mathrm{2}?\mathrm{s}\mathrm{i}\mathrm{n}(?\mathrm{\pi }{?}_{?})}{??\mathrm{\pi }{?}_{?}}??$(33f)

到此2个最重要的Fourier系数(B0、Bn)表达式已经导出。可以看出，B0的物理含义是2个共晶固相从液相里析出后，排到界面的溶质量的绝对值差，当两相分数符合$\mathrm{\Delta }{?}_{?}{?}_{?}=\mathrm{\Delta }{?}_{?}{?}_{?}$时，B0=0。Bn的含义是界面溶质富集浓度的振幅大小，显然V越大，浓度振幅Bn越大，说明界面溶质富集的程度越严重；但是CB减小可以缩小振幅，所以系统为了平衡，常常生长速率越大，CB值越小。反过来说，含有化合物相的共晶相图区间越窄，共晶生长速率越大。

1.4 界面液相的平均溶质浓度的计算

接下来计算过冷度和生长速率的关系时需要求解凝固界面的成分过冷，成分过冷与各相界面前沿的平均成分有关。可以发现，当V较小时，$?\mathrm{\pi }/({?}_{?}+{?}_{?})??/(\mathrm{2}?)$，这时式(23)中ωn表达式可被简化，界面成分式(24b)可写成：

$?(?,?)={?}_{\mathrm{\infty }}+{?}_{\mathrm{0}}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{?}{?}?\right)+$${\displaystyle \sum _{?=\mathrm{1}}^{\mathrm{\infty }}}{?}_{?}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{?\mathrm{\pi }?}{{?}_{?}+{?}_{?}}\right)\mathrm{c}\mathrm{o}\mathrm{s}\left(\frac{?\mathrm{\pi }?}{{?}_{?}+{?}_{?}}\right)$(34)

当z = 0时，界面处沿着x方向的浓度分布函数关系为：

$?(?,\mathrm{0})={?}_{\mathrm{\infty }}+{?}_{\mathrm{0}}+{\displaystyle \sum _{?=\mathrm{1}}^{\mathrm{\infty }}}{?}_{?}\mathrm{c}\mathrm{o}\mathrm{s}(\frac{?\mathrm{\pi }?}{{?}_{?}+{?}_{?}})$(35)

对α相界面$\mathrm{0}\le ?\le {?}_{?}$范围的平均浓度${\overline{?}}_{?}$求解，是通过对界面处x方向的浓度先积分再平均获得：

${\overline{?}}_{?}={?}_{\mathrm{\infty }}+{?}_{\mathrm{0}}+\frac{\mathrm{1}}{{?}_{?}}{\displaystyle \underset{\mathrm{0}}{\overset{{?}_{?}}{\int }}}{\displaystyle \sum _{?=\mathrm{1}}^{\mathrm{\infty }}}{?}_{?}\mathrm{c}\mathrm{o}\mathrm{s}(\frac{?\mathrm{\pi }?}{{?}_{?}+{?}_{?}})\mathrm{d}?=$${?}_{\mathrm{\infty }}+{?}_{\mathrm{0}}+\frac{\mathrm{1}}{{?}_{?}}{\displaystyle \sum _{?=\mathrm{1}}^{\mathrm{\infty }}}{?}_{?}\frac{{?}_{?}+{?}_{?}}{?\mathrm{\pi }}\mathrm{s}\mathrm{i}\mathrm{n}\frac{?\mathrm{\pi }{?}_{?}}{{?}_{?}+{?}_{?}}$(36a)

同理，对β相界面，${?}_{?}\le ?\le {?}_{?}+{?}_{?}$范围的平均浓度${\overline{?}}_{?}$可表示为，

${\overline{?}}_{?}={?}_{\mathrm{\infty }}+{?}_{\mathrm{0}}+\frac{\mathrm{1}}{{?}_{?}}{\displaystyle \underset{{?}_{?}}{\overset{{?}_{?}+{?}_{?}}{\int }}}{\displaystyle \sum _{?=\mathrm{1}}^{\mathrm{\infty }}}{?}_{?}\mathrm{c}\mathrm{o}\mathrm{s}(\frac{?\mathrm{\pi }?}{{?}_{?}+{?}_{?}})\mathrm{d}?=$${?}_{\mathrm{\infty }}+{?}_{\mathrm{0}}-\frac{\mathrm{1}}{{?}_{?}}{\displaystyle \sum _{?=\mathrm{1}}^{\mathrm{\infty }}}{?}_{?}\frac{{?}_{?}+{?}_{?}}{?\mathrm{\pi }}\mathrm{s}\mathrm{i}\mathrm{n}\frac{?\mathrm{\pi }{?}_{?}}{{?}_{?}+{?}_{?}}$(36b)

将式(33b)的Bn带入得到两相界面平均浓度：

${\overline{?}}_{?}={?}_{\mathrm{\infty }}+{?}_{\mathrm{0}}+\frac{\mathrm{2}({?}_{?}+{?}_{?}{)}^{\mathrm{2}}}{{?}_{?}}\frac{?}{?}\cdot$$\left[(\mathrm{1}-{?}_{?}^{}){?}_{\mathrm{E}}+(\mathrm{1}-{?}_{?}^{})(??-{?}_{\mathrm{E}})\right]?$(37a)${\overline{?}}_{?}={?}_{\mathrm{\infty }}+{?}_{\mathrm{0}}-\frac{\mathrm{2}({?}_{?}+{?}_{?}{)}^{\mathrm{2}}}{{?}_{?}}\frac{?}{?}\cdot$$\left[(\mathrm{1}-{?}_{?}^{}){?}_{\mathrm{E}}+(\mathrm{1}-{?}_{?}^{})(??-{?}_{\mathrm{E}})\right]?$(37b)$?={\displaystyle \sum _{?=\mathrm{1}}^{\mathrm{\infty }}}{(\frac{\mathrm{1}}{?\mathrm{\pi }})}^{\mathrm{3}}\mathrm{s}\mathrm{i}{\mathrm{n}}^{\mathrm{2}}(\frac{?\mathrm{\pi }{?}_{?}}{{?}_{?}+{?}_{?}})$(38)

1.5 过冷度、生长速率及层片间距的关系

对于共晶凝固界面前沿的过冷度，JH模型只考虑了界面成分富集引起的成分过冷(ΔTc)和界面前沿弯曲负压引起的曲率过冷(ΔTr)，把界面总过冷$\mathrm{\Delta }?$表示为：

$\mathrm{\Delta }{?}_{}=\mathrm{\Delta }{?}_{\mathrm{c}}+\mathrm{\Delta }{?}_{\mathrm{r}}$(39)

在α相界面前沿的液相中，

$\mathrm{\Delta }{?}_{?}={?}_{?}({\overline{?}}_{?}-{?}_{\mathrm{E}})+\frac{{?}_{?}\mathrm{s}\mathrm{i}\mathrm{n}{?}_{?}}{{?}_{?}}$(40a)

在β相界面前沿的液相中，

$\mathrm{\Delta }{?}_{?}={?}_{?}({?}_{\mathrm{E}}-{\overline{?}}_{?})+\frac{{?}_{?}\mathrm{s}\mathrm{i}\mathrm{n}{?}_{?}}{{?}_{?}}$(40b)

式中，mα和mβ分别对应相图上的α相、β相的液相线斜率，Γα和Γβ为Gibbs-Thomson系数，θα和θβ是三相点处α相、β相和液相的接触角。将式(37a)和(37b)分别带入式(40a)和(40b)可得：

$\mathrm{\Delta }{?}_{?}={?}_{?}\left\{{?}_{\mathrm{\infty }}+{?}_{\mathrm{0}}+\frac{\mathrm{2}({?}_{?}+{?}_{?}{)}^{\mathrm{2}}}{{?}_{?}}\frac{?}{?}\left[(\mathrm{1}-{?}_{?}^{}){?}_{\mathrm{E}}+(\mathrm{1}-{?}_{?}^{})(??-{?}_{\mathrm{E}})\right]?-{?}_{\mathrm{E}}\right\}+\frac{{?}_{?}\mathrm{s}\mathrm{i}\mathrm{n}{?}_{?}}{{?}_{?}}$(41a)$\mathrm{\Delta }{?}_{?}={?}_{?}\left\{{?}_{\mathrm{E}}-{?}_{\mathrm{\infty }}-{?}_{\mathrm{0}}+\frac{\mathrm{2}({?}_{?}+{?}_{?}{)}^{\mathrm{2}}}{{?}_{?}}\frac{?}{?}\left[(\mathrm{1}-{?}_{?}^{})\cdot {?}_{\mathrm{E}}+(\mathrm{1}-{?}_{?}^{})(??-{?}_{\mathrm{E}})\right]?\right\}+\frac{{?}_{?}\mathrm{s}\mathrm{i}\mathrm{n}{?}_{?}}{{?}_{?}}$(41b)

假设两相界面前沿液相的过冷度和生长速率都相等，即$\mathrm{\Delta }{?}_{?}$ = $\mathrm{\Delta }{?}_{?}$ = $\mathrm{\Delta }?$。由于层片间距为λ = 2(Sα+ Sβ)，将式(41a)和(41b)联立消去C∞和B0得[4]：

$\frac{\mathrm{\Delta }?}{?}=??{?}^{\mathrm{L}}+\frac{{?}^{\mathrm{L}}}{?}$(42)

其中：

${?}^{\mathrm{L}}=\mathrm{2}(\frac{{?}_{?}\mathrm{s}\mathrm{i}\mathrm{n}{?}_{?}}{{?}_{?}{?}_{?}}+\frac{{?}_{?}\mathrm{s}\mathrm{i}\mathrm{n}{?}_{?}}{{?}_{?}{?}_{?}})$(43)${?}^{\mathrm{L}}=\frac{\mathrm{1}}{{?}_{?}{?}_{?}}\frac{(\mathrm{1}-{?}_{?}^{}){?}_{\mathrm{E}}+(\mathrm{1}-{?}_{?}^{})(??-{?}_{\mathrm{E}})}{?}?$(44)$\frac{\mathrm{1}}{?}=\frac{\mathrm{1}}{{?}_{?}}+\frac{\mathrm{1}}{{?}_{?}}$(45)

假设共晶生长是在最小过冷度下进行，对于式(42)，过冷度要取最小值，由Cauchy不等式，只有在 $?{?}^{\mathrm{L}}?$ = ${?}^{\mathrm{L}}/?$时，式(42)中的ΔT才可获得最小值，即：

$?{?}^{\mathrm{2}}=\frac{{?}^{\mathrm{L}}}{{?}^{\mathrm{L}}}$(46a)

带入式(43)和(44)可得：

$?{?}^{\mathrm{2}}=\frac{\mathrm{2}?{?}_{?}{?}_{?}[{?}_{?}\mathrm{s}\mathrm{i}\mathrm{n}{?}_{?}/({?}_{?}{?}_{?})+{?}_{?}\mathrm{s}\mathrm{i}\mathrm{n}{?}_{?}/({?}_{?}{?}_{?})]}{(\mathrm{1}-{?}_{?}^{}){?}_{\mathrm{E}}+(\mathrm{1}-{?}_{?}^{})(??-{?}_{\mathrm{E}})}\frac{\mathrm{1}}{?}$(46b)

为了方便计算，Trivedi等[26]把方程(38)函数简化为P = 0.3383(fα fβ)1.661，带入上式，可得到共晶转变动力学的核心关系式：

$?{?}^{\mathrm{2}}=\left\{\mathrm{5.912}?[{?}_{?}\mathrm{s}\mathrm{i}\mathrm{n}{?}_{?}/({?}_{?}{?}_{?})+\right.$$\left.{?}_{?}\mathrm{s}\mathrm{i}\mathrm{n}{?}_{?}/({?}_{?}{?}_{?})]\right\}/\left[(\mathrm{1}-{?}_{?}^{}){?}_{\mathrm{E}}+\right.$$\left.(\mathrm{1}-{?}_{?}^{})(??-{?}_{\mathrm{E}})\right]\cdot ({?}_{?}{?}_{?}{)}^{-\mathrm{0.661}}$(46c)

方程(42)~(46)即为考虑金属间化合物相存在的共晶生长模型。这里相分数可由相图杠杆定律近似求得，即${?}_{?}$ = $({?}_{\mathrm{s}?}-{?}_{\mathrm{\infty }})/({?}_{\mathrm{s}?}-{?}_{\mathrm{s}?})$，这是经典模型中唯一体现合金原始成分对共晶生长影响的地方。JH模型虽然主要用在中低速共晶生长情况，但是对各类共晶相图都适用，使用方便，无需计算机编程也能求解。方程(46)和原JH模型相比，主要是把ΔC0项换成了$(\mathrm{1}-{?}_{?}^{}){?}_{\mathrm{E}}+(\mathrm{1}-{?}_{?}^{})(??-{?}_{\mathrm{E}})$。如果不考虑固溶度和溶质分配系数随生长速率改变，上述表达式中的$(\mathrm{1}-{?}_{?}^{}){?}_{\mathrm{E}}+(\mathrm{1}-{?}_{?}^{})(??-{?}_{\mathrm{E}})$可以写成$({?}_{\mathrm{s}?}-{?}_{\mathrm{s}?})$，这个值可直接从相图中读取，也适用于相图两端都是化合物相的情况，但在高速共晶生长模型中[7,13,23]溶质分配系数会随生长速率变化而改变，不能从相图中直接获得。

2 适用高速共晶生长的模型

2.1 LZ模型

目前众多考虑高速共晶生长的模型中LZ模型[10]是形式较简单的一种，与上述推导过程类似，可以导出有化合物相参与的LZ模型方程：

$\begin{array}{l}\mathrm{\Delta }?=\mathrm{\Delta }{?}_{\mathrm{c}}+\mathrm{\Delta }{?}_{\mathrm{r}}+\mathrm{\Delta }{?}_{\mathrm{k}}+\mathrm{\Delta }{?}_{\mathrm{t}}=\\ ?\left[\left({?}_{\mathrm{0}}^{\mathrm{L}}?+\frac{\mathrm{1}}{?}\right)?+\frac{{?}^{\mathrm{L}}}{?}\right]+\frac{\mathrm{\Delta }?}{{?}_{?}}??({?}_{?})\end{array}$(47)${?}_{\mathrm{0}}^{\mathrm{L}}=\frac{(\mathrm{1}-{?}_{?}^{}){?}_{\mathrm{E}}+(\mathrm{1}-{?}_{?}^{})(??-{?}_{\mathrm{E}})}{{?}_{?}{?}_{?}}\frac{?}{?}$(48)$?=\left\{\begin{array}{l}{\displaystyle \sum _{?=\mathrm{1}}^{\mathrm{\infty }}}\frac{\mathrm{s}\mathrm{i}{\mathrm{n}}^{\mathrm{2}}\left(?\mathrm{\pi }{?}_{?}\right)}{{(?\mathrm{\pi })}^{\mathrm{3}}}\frac{{?}_{?}}{\sqrt[]{\mathrm{1}+{?}_{?}^{\mathrm{2}}}+\mathrm{1}}\\ (\mathrm{C}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{I}:\mathrm{C}\mathrm{i}\mathrm{g}\mathrm{a}\mathrm{r}\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e})\\ {\displaystyle \sum _{?=\mathrm{1}}^{\mathrm{\infty }}}\frac{\mathrm{s}\mathrm{i}{\mathrm{n}}^{\mathrm{2}}\left(?\mathrm{\pi }{?}_{?}\right)}{{(?\mathrm{\pi })}^{\mathrm{3}}}\frac{{?}_{?}}{\sqrt[]{\mathrm{1}+{?}_{?}^{\mathrm{2}}}-\mathrm{1}+\mathrm{2}?}\\ (\mathrm{C}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{I}\mathrm{I}:{?}_{?}={?}_{?})\end{array}\right.$(49)

式中，ΔTk和ΔTt分别是动力学过冷度和热力学过冷度；μ是动力学系数；ΔH是熔化热；cp是液相比热容；$??({?}_{?})$是Ivantsov解[10]；pn = 2nπ / Pe，Pe是共晶合金Peclet数，Pe = Vλ/(2D)；k是随生长速率改变的溶质分配系数。根据最小过冷生长原理，对方程(47)采用Cauchy不等式可得到式(50)~(52)。

这里Case I适用于“雪茄型”(Cigar shape)相图[10]，也就是共晶温度以下，液相线和固相线延长线平行的情况，这类相图的特点是固溶度大或者溶质平衡分配系数较大。Case II适用于“等溶质分配系数型”相图，这类相图特点是平衡溶质分配系数一般不大，两相固溶度比较小，含有金属间化合物相的绝大多数共晶转变属于这类，所以大多模型计算文献都以这类相图为主开发研究[10,16]。当生长速率变小的时候，动力学过冷度和热力学过冷度的影响可以忽略，于是这个模型回归到TMK模型[6]，当生长速率很小时，方程(49)和(52)中的pn会趋于无穷大，这时TMK模型会趋于和JH模型相同的结果。

2.2 LNM模型

实验中发现，共晶转变在V ≥ VD (VD为体溶质扩散速率)时，扩散控制的共晶转变会被突然抑制，变成无扩散生长，形成浓度分布均匀的单相组织[21]，于是，在界面溶质局部非平衡分布假设的条件下可以获得LNM模型，这个模型与LZ模型的区别主要在于，函数P及其导数表达式引入了参数VD，VD值限制了共晶生长最高速率[22,23]，见式(53)和(54)。

这里pn = 4nπD /(Vλ)。LNM模型主要包含了从较小生长速率到极大生长速率的转变，直至溶质扩散被抑制形成成分均匀相的情况，模型中考虑了两相的固溶度和溶质分配系数变化，但是需要计算机编程迭代计算方能求解。

$?{?}^{\mathrm{2}}={?}^{\mathrm{L}}/{?}_{\mathrm{L}\mathrm{Z}}^{\mathrm{L}}$(50)${?}_{\mathrm{L}\mathrm{Z}}^{\mathrm{L}}=\frac{(\mathrm{1}-{?}_{?}^{}){?}_{\mathrm{E}}+(\mathrm{1}-{?}_{?}^{})(??-{?}_{\mathrm{E}})}{{?}_{?}{?}_{?}?}(?+?\frac{\partial ?}{\partial ?})$(51)$?+?\frac{\partial ?}{\partial ?}=\left\{\begin{array}{l}{\displaystyle \sum _{?=\mathrm{1}}^{\mathrm{\infty }}}\frac{\mathrm{s}\mathrm{i}{\mathrm{n}}^{\mathrm{2}}\left(?\mathrm{\pi }{?}_{?}\right)}{{(?\mathrm{\pi })}^{\mathrm{3}}}{\left(\frac{{?}_{?}}{\sqrt[]{\mathrm{1}+{?}_{?}^{\mathrm{2}}}+\mathrm{1}}\right)}^{\mathrm{2}}\frac{{?}_{?}}{\sqrt[]{\mathrm{1}+{?}_{?}^{\mathrm{2}}}}(\mathrm{C}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{I})\\ {\displaystyle \sum _{?=\mathrm{1}}^{\mathrm{\infty }}}\frac{\mathrm{s}\mathrm{i}{\mathrm{n}}^{\mathrm{2}}\left(?\mathrm{\pi }{?}_{?}\right)}{{(?\mathrm{\pi })}^{\mathrm{3}}}{\left(\frac{{?}_{?}}{\sqrt[]{\mathrm{1}+{?}_{?}^{\mathrm{2}}}-\mathrm{1}+\mathrm{2}?}\right)}^{\mathrm{2}}\frac{{?}_{?}}{\sqrt[]{\mathrm{1}+{?}_{?}^{\mathrm{2}}}}(\mathrm{C}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{I}\mathrm{I})\end{array}\right.$(52)$?=\left\{\begin{array}{l}{\displaystyle \sum _{?=\mathrm{1}}^{\mathrm{\infty }}}\frac{\mathrm{s}\mathrm{i}{\mathrm{n}}^{\mathrm{2}}\left(?\mathrm{\pi }{?}_{?}\right)}{{(?\mathrm{\pi })}^{\mathrm{3}}}\frac{{?}_{?}}{\sqrt[]{\mathrm{1}+{\left[{?}_{?}\left(\mathrm{1}-{?}^{\mathrm{2}}/{?}_{\mathrm{D}}^{\mathrm{2}}\right)\right]}^{\mathrm{2}}}+\mathrm{1}}(\mathrm{C}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{I})\\ {\displaystyle \sum _{?=\mathrm{1}}^{\mathrm{\infty }}}\frac{\mathrm{s}\mathrm{i}{\mathrm{n}}^{\mathrm{2}}\left(?\mathrm{\pi }{?}_{?}\right)}{{(?\mathrm{\pi })}^{\mathrm{3}}}\frac{{?}_{?}}{\sqrt[]{\mathrm{1}+{\left[{?}_{?}\left(\mathrm{1}-{?}^{\mathrm{2}}/{?}_{\mathrm{D}}^{\mathrm{2}}\right)\right]}^{\mathrm{2}}}-\mathrm{1}+\mathrm{2}?}(\mathrm{C}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{I}\mathrm{I})\end{array}\right.$(53)$?+?\frac{\partial ?}{\partial ?}=\left\{\begin{array}{l}{\displaystyle \sum _{?=\mathrm{1}}^{\mathrm{\infty }}}\frac{\mathrm{s}\mathrm{i}{\mathrm{n}}^{\mathrm{2}}\left(?\mathrm{\pi }{?}_{?}\right)}{{(?\mathrm{\pi })}^{\mathrm{3}}}{\left(\frac{{?}_{?}\left(\mathrm{1}-{?}^{\mathrm{2}}/{?}_{\mathrm{D}}^{\mathrm{2}}\right)}{\sqrt[]{\mathrm{1}+{\left[{?}_{?}\left(\mathrm{1}-{?}^{\mathrm{2}}/{?}_{\mathrm{D}}^{\mathrm{2}}\right)\right]}^{\mathrm{2}}}+\mathrm{1}}\right)}^{\mathrm{2}}\frac{{?}_{?}}{\sqrt[]{\mathrm{1}+{\left[{?}_{?}\left(\mathrm{1}-{?}^{\mathrm{2}}/{?}_{\mathrm{D}}^{\mathrm{2}}\right)\right]}^{\mathrm{2}}}}(\mathrm{C}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{I})\\ {\displaystyle \sum _{?=\mathrm{1}}^{\mathrm{\infty }}}\frac{\mathrm{s}\mathrm{i}{\mathrm{n}}^{\mathrm{2}}\left(?\mathrm{\pi }{?}_{?}\right)}{{(?\mathrm{\pi })}^{\mathrm{3}}}{\left(\frac{{?}_{?}\left(\mathrm{1}-{?}^{\mathrm{2}}/{?}_{\mathrm{D}}^{\mathrm{2}}\right)}{\sqrt[]{\mathrm{1}+{\left[{?}_{?}\left(\mathrm{1}-{?}^{\mathrm{2}}/{?}_{\mathrm{D}}^{\mathrm{2}}\right)\right]}^{\mathrm{2}}}-\mathrm{1}+\mathrm{2}?}\right)}^{\mathrm{2}}\frac{{?}_{?}}{\sqrt[]{\mathrm{1}+{\left[{?}_{?}\left(\mathrm{1}-{?}^{\mathrm{2}}/{?}_{\mathrm{D}}^{\mathrm{2}}\right)\right]}^{\mathrm{2}}}}(\mathrm{C}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{I}\mathrm{I})\end{array}\right.$(54)

3 溶质分配系数和液相线斜率

一般在给定温度和压强下溶质分配系数定义为ke = Cs / Cl，这里Cs和Cl分别为固相和液相在平衡位置的浓度。这个表达式适用条件是相图上的液相线和固相线都是直线，而且共晶相图两端浓度是0和1。而实际中的相图固相线和液相相线往往并非直线，纯化合物相一端成分小于1。Trivedi和Kurz[27]在研究各种相图后，提供了确定这类相图溶质分配系数的方法。一种是采用kα = Csα/CE和kβ = (CB-Csβ) / (CB - CE)，这里Csα和Csβ是两相在共晶温度的平衡浓度。另一种方法是无论对α还是β相的分配系数都用液相线斜率(ml)和固相线斜率(ms)的比值来确定，即ke = ml/ ms。为了保证kβ < 1，在确定β相的分配系数时，一般把相图左右镜面反转过来计算。对于液固相线明显弯曲的相图可以采用图3所示的方法[27]，把液相线和固相线进行反向延长，找到交点浓度aα和aβ，然后采用k${}_{?}^{}$ = (Csα - aα) / (CE - aα)，k${}_{?}^{}$= (Csβ - aβ) / (CE - aβ)求得。

图3

图3   溶质分配系数的确定方法示意图

Fig.3   Schematic diagram for determining solute distribution coefficient (αα and αβ are the points where the liquid phase and the solid phase intersect)

研究表明，随着生长速率增加，凝固界面的两相成分会受到界面溶质扩散速率(VDI)的影响，Aziz[28]给出考虑生长速率与溶质分配系数表达式：

$?(?)=\frac{{?}_{\mathrm{e}}+?/{?}_{\mathrm{D}\mathrm{I}}^{}}{\mathrm{1}+?/{?}_{\mathrm{D}\mathrm{I}}^{}}$(55a)

共晶两相的液相线斜率也会受到生长速率的影响，其表达式为：

${?}^{\mathrm{v}}=?[\frac{\mathrm{1}-?[\mathrm{1}-\mathrm{l}\mathrm{n}(?/{?}_{\mathrm{e}})]}{\mathrm{1}-{?}_{\mathrm{e}}}]$(55b)

这里${?}^{\mathrm{v}}$表示受生长速率影响的液相线斜率。方程(55a)和(55b)可以用于LZ模型中考虑生长速率对固溶度和溶质分配系数影响的情况。

在生长速率不是非常大的情况下，式(55a)与实验相符[29]。但是，在超快速凝固条件下(V > VD)，人们发现k(V)可以达到1，且合金熔体会完全变成浓度均匀的单相组织[21]。而方程(55a)计算结果永远小于1，与实际偏离。于是基于松弛的Fick定律可以得到溶质分配系数新的表达式[23]：

$?(?,{?}_{?})=\left\{\begin{array}{l}\frac{(\mathrm{1}-{?}^{\mathrm{2}}/{?}_{\mathrm{D}}^{\mathrm{2}})[{?}_{\mathrm{e}}+(\mathrm{1}-{?}_{\mathrm{e}}){?}_{\mathrm{s}}]+?/{?}_{\mathrm{D}\mathrm{I}}}{\mathrm{1}-{?}^{\mathrm{2}}/{?}_{\mathrm{D}}^{\mathrm{2}}+?/{?}_{\mathrm{D}\mathrm{I}}}(?<{?}_{\mathrm{D}})\\ \mathrm{1}(?\ge {?}_{\mathrm{D}})\end{array}\right.$(56a)

这里Cs等于Csα或Csβ。当VD→∞时，式(56a)趋于式(55a)。共晶两相的液相线斜率与生长速率关系为[23]：

${?}^{\mathrm{v}}=?\frac{\mathrm{1}-?+\mathrm{l}\mathrm{n}(?/{?}_{\mathrm{e}})+[(\mathrm{1}-?)(?/{?}_{\mathrm{D}}{)]}^{\mathrm{2}}}{\mathrm{1}-{?}_{\mathrm{e}}}$(56b)

当共晶生长考虑溶质拖拽时，需采用LNM模型，先采用式(56)计算局部非平衡条件下的溶质分配系数和液相线斜率，然后采用方程(47)、(50)、(51)、(53)和(54)计算$\mathrm{\Delta }$T-V-λ之间的关系。

4 模型计算与讨论

4.1 共晶生长动力学的计算

为具有代表性，这里选择2种含有化合物相的共晶合金进行生长动力学计算，一种是kα和kβ不为0的Al-Al2Cu合金[30]，见图4a；另一种是kα = kβ = 0的CuZr-CuZr2合金[31]，见图4b。计算参数如表1[30]所示。使用JH模型，首先计算Al-Al2Cu合金溶质分配系数，${?}_{?}$ = ${?}_{\mathrm{s}?}/{?}_{\mathrm{E}}$ = 0.146，${?}_{?}$ = $(??-{?}_{\mathrm{s}?})$ / $(??-{?}_{\mathrm{E}})$ = 0.0864。接着计算两相体积分数：${?}_{?}$ = (${?}_{\mathrm{s}?}$ - ${?}_{\mathrm{\infty }}$) / (${?}_{\mathrm{s}?}-{?}_{\mathrm{s}?}$) = 0.503，${?}_{?}$ = $({?}_{\mathrm{\infty }}-{?}_{\mathrm{s}?})/({?}_{\mathrm{s}?}-{?}_{\mathrm{s}?})$ = 0.497。通过方程(43)求出${?}^{\mathrm{L}}$，通过方程(44)求出${?}^{\mathrm{L}}$，再通过方程(46)获得V-λ关系。把方程(46a)带入方程(42)可以获得ΔT-V和ΔT-λ的关系，结果如图5a和5b所示。

图4

图4   Al-Al2Cu合金相图[30]和CuZr-CuZr2合金相图[31]

Fig.4   Phase diagrams of Al-Al2Cu alloy[30] (a) and CuZr-CuZr2 alloy[31] (b) (T—temperature)

表1   Al-Al2Cu合金相关物理参数[30]

Table 1  The parameters for the model calculation of Al-Al2Cu eutectic growth[30]

Parameter	Unit	Value	Parameter	Unit	Value
Csα	%	2.5	Csβ	%	31.9
mα	K·%-1	6.48	TE	K	812
mβ	K·%-1	6.70	CE	%	17.1
CB	%	33.33	C∞	%	17.1
Γα	K·m	2.358 × 10-7	α	m2·s-1	1.5 × 10-6
Γβ	K·m	5.54 × 10-8	D	m2·s-1	3 × 10-9
θα	(°)	70	θβ	(°)	52

Note: Here % refers to the atomic fraction (the same below); Γα and Γβ are the Gibbs-Thomson coefficients; α is thermal diffusion coefficient; C∞ is the concentration in the liquid far from the interface; D is the diffusion coefficient

新窗口打开| 下载CSV

图5

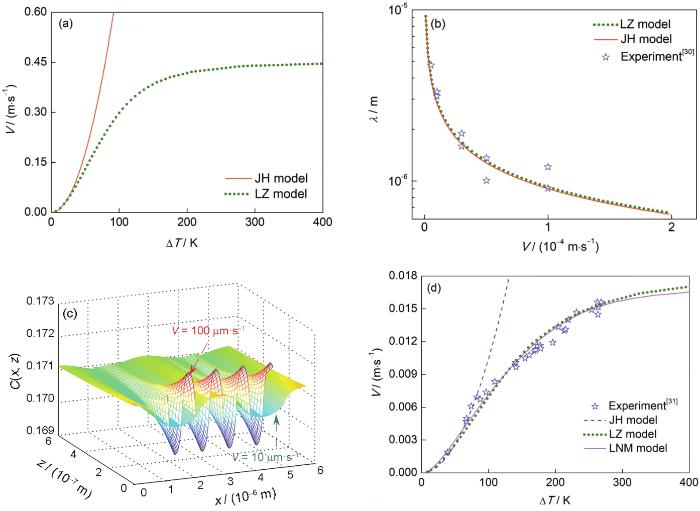
图5   实验与计算结果对比

(a) ΔT-V curves of Al-Al2Cu alloy (ΔT—undercooling)

(b) V-λ curves of Al-Al2Cu alloy and experimental data[30]

(c) interfacial concentration distribution C(x, z) of Al-Al2Cu alloy at two growth rates

(d) calculation results and experiments[31] of CuZr-CuZr2 alloy

Fig.5   Results of the experiments and calculation of alloys

对LZ模型计算也是先通过方程(43)求出${?}^{\mathrm{L}}$，再通过方程(51)求得${?}_{\mathrm{L}\mathrm{Z}}^{\mathrm{L}}$，带入方程(50)求得V-λ关系。因为方程(52)中的pn包含生长速率(= 4nπD /(Vλ))，需要通过迭代法获得V和λ的对应关系。也就是把方程(50)变形为λ = $\sqrt[]{{?}^{\mathrm{L}}/({?}_{\mathrm{L}\mathrm{Z}}^{\mathrm{L}}\cdot ?)}$，给定一个V，把初值λ0带入等式右边根号里的${?}_{\mathrm{L}\mathrm{Z}}^{\mathrm{L}}$表达式，计算出左边的λ1，再把λ1带入等式右边根号，这样反复计算，直到收敛为一个稳定的λ。再把获得的V-λ数据带入式(47)可以进而获得对应的ΔT。如果给出许多V，会得到许多对应的λ和ΔT，从而可以画出ΔT-V和V-λ的关系，如图5a和b所示。与实验数据[30]进行对比，2个模型计算结果与实验都吻合良好，因为这里的数据都是小生长速率情况。图5c是通过计算获得生长速率分别为10和100 μm/s的界面溶质浓度分布图。可以看出，生长速率大的界面溶质富集严重，振幅较大，而层片间距较小。

对于生长速率较大的CuZr-CuZr2合金，本工作采用3种模型进行计算，参数如表2[31]所示。对LNM模型的计算，首先从相图可知kα = kβ=0，带入方程(56)可得到任意生长速率下的k和m。然后给定一个生长速率V，和层片间距的一个初值λ0=0.0001，带入方程(54)获得$?+?(\partial ?/\partial ?)$，然后把所得值和其他参数带入方程(51)求得${?}_{\mathrm{L}\mathrm{Z}}^{\mathrm{L}}$，再带入方程(50)的变形式$?=\sqrt[]{{?}^{\mathrm{L}}/({?}_{\mathrm{L}\mathrm{Z}}^{\mathrm{L}}\cdot ?)}$求得一个λ1，再把这个λ1依次带入方程(56)、(54)、(51)、(50)计算下一个λ2，反复迭代计算，直到λ几乎不变，即可获得给定V对应的λ。然后把所得V-λ带入方程(47)，即得ΔT-V和ΔT-λ的关系。计算结果和实验数据对比如图5d所示。可以看出，JH模型计算结果在低生长速率范围与实验数据吻合良好，但在高生长速率范围，LZ模型和LNM模型结果与实验数据吻合良好。

表2   CuZr-CuZr2合金相关物理参数[31]

Table 2  The parameters for the model calculation of CuZr-CuZr2 eutectic growth[31]

Parameter	Unit	Value	Parameter	Unit	Value
Γα	K·m	2.2 × 10-7	Csα	%	2.5
Γβ	K·m	2.2 × 10-7	Csβ	%	31.9
mα	K·%-1	3.02	TE	K	1195
mβ	K·%-1	6.47	α	m2·s-1	1.5 × 10-6
θα	(°)	45	μα	m·K-1·s-1	0.1
θβ	(°)	45	μβ	m·K-1·s-1	0.1
CB	%	66.67	VD	m·s-1	0.12
C∞	%	54	CE	%	54.3

Note:μα and μβ are the kinetic coefficients, VD is the solute diffusion speed

新窗口打开| 下载CSV

4.2 化合物相成分CB对共晶转变的影响

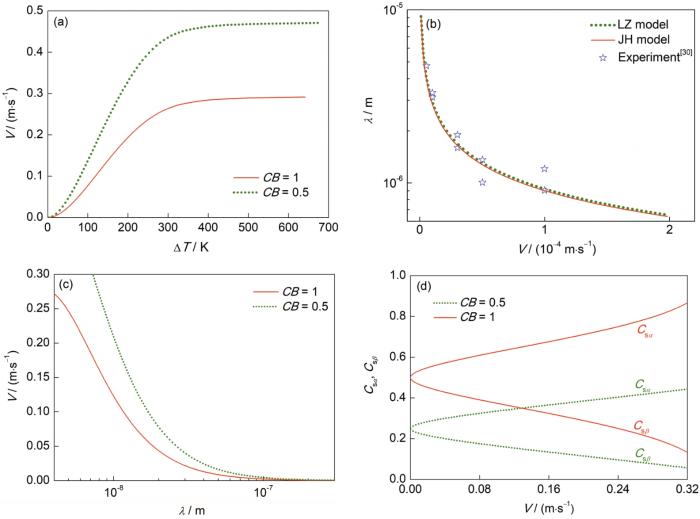
为了研究相图右端化合物浓度CB对生长速率的影响，假设相图溶质分配系数和各相熔点不变，只改变化合物浓度，即采用参数CB、kα、kβ、mα、mβ、TE、μα、μβ分别为0.5、0.004、0.004、450、450、1400、0.05、0.05和CB、kα、kβ、mα、mβ、TE、μα、μβ分别为1、0.004、0.004、225、225、1400、0.05、0.05，借助LZ模型进行计算，获得结果如图6所示。可以看出，化合物相成分CB越小，生长速率明显越大(图6a)，但是对ΔT-λ曲线影响很小(图6b)。CB越小，共晶生长中，固相前沿的液相里需要扩散出去的溶质(Cl - Cs)也越少，这样生长会变得容易。这一参数引起的变化弥补了一般化合物相因溶质分配系数小而生长阻力大的不足。由此推测出2个规律：有复杂合金化合相的共晶相图成分跨度会变窄，在一定成分范围内会被分成多个共晶相图；ke越小的共晶相图越窄，例如Ni-B、Fe-B和Co-B合金[32~35]都是如此。另一类例子是成分跨度不变窄的共晶系统的ke不能小，也就是Csα较大，例如Fe-C相图存在化合物相Fe3C，两端跨度很宽，原因是ke较大，C在Fe里固溶度很大，发生共晶生长时需排出溶质(Cl - Cs)实际并不多，在较宽的浓度区间仍然能够保持界面高速生长。

图6

图6   化合物相浓度CB对计算结果的影响

(a) ΔT-V curve (b) ΔT-λ curve (c) λ-V curve (d) V-Csα(Csβ) curve

Fig.6   Influence of composition CB on the calculation results at the two-phase interfaces

5 结论

在经典理论模型基础上，推导了有化合物相参与的共晶转变情况，补充了JH模型推导中省略的Fourier系数B0和Bn求解过程。采用JH模型计算含有化合物相的共晶生长，没有特殊相图限制；在计算上简单易行，但适用于中低生长速率的共晶转变。采用LZ模型以及考虑溶质局部非平衡分布的LNM模型，能更准确地描述高速共晶生长实验数据，但是这2个模型适用条件为“雪茄型”和“等溶质分配系数型”相图，而且计算过程需要迭代。数值计算发现，化合物相浓度CB减小，共晶生长速率增大，这一参数变化弥补了化合物相因溶质分配系数小而生长阻力大的不足。由此得出：有复杂化合相的共晶相图会变窄；共晶相的溶质分配系数越小的共晶相图越窄。

来源--金属学报