分享:Mg-4.4Li-2.5Zn-0.46Al-0.74Y合金高温变形流动应力、组织演变与本构分析
1.
2.
3.
4.
由于密度低,很大的比刚度,良好的比强度、阻尼性能与电磁屏蔽性能,Mg-Li合金在航天卫星、电子、汽车等轻量化的领域获得了应用。α(Mg)基体的Mg-Li合金含Li量低于5.7% (质量分数,下同),双相α(Mg) + β(Li)基体的Mg-Li合金含Li量介于5.7%~11.0%之间,β(Li)基体的Mg-Li合金含Li量大于11.0%。Mg和α(Mg)基合金室温仅有2个滑移系,难以满足5个滑移系的变形协调要求,因而室温成形困难。有必要采用高温变形解决α(Mg)基Mg-Li合金成形性问题。近来Mg-Li-Zn系合金设计与组织性能研究引起了研究者的关注,目前报道的多为单相β(Li)基体[1]和双相α(Mg) + β(Li)基体[2~4]的合金,对α(Mg)基Mg-Li-Zn合金报道很少。多向锻造(MDF)是剧烈塑性变形方法之一。与高压扭转和等通道转角挤压方法适用于小尺寸试样相比,MDF适合于大尺寸试样的成形,对工业规模的应用具有价值,因此,近来镁合金MDF成形与组织性能研究引起研究者的注意,包括Mg-Gd-Y[5,6]、Mg-9Al[7]、AZ80-F[8]镁合金MDF晶粒细化与力学性能,而MDF晶粒细化机理阐述有待进一步研究。近年来双相α(Mg) + β(Li) Mg-Li-Zn合金超塑性研究取得新进展[9~11]。研究者分别采用MDF[9]、挤压+轧制[10]与搅拌摩擦加工[11]方法实现双相合金晶粒细化并获得超塑性。但是,除了本文作者前期提出的多向锻造+轧制 (MDFR)方法制备双相α(Mg) + β(Li) Mg-Li合金研究室温组织性能[12]与超塑性[13]报道以外,尚未见到α(Mg)基准单相Mg-Li-Zn-Al-Y合金MDFR成形与高温组织性能的研究报道。
本构模型反映了应力与温度和应变速率之间的关系,是高温变形过程计算变形力与模拟必不可少的模型。本构模型包括唯象学本构、物理基本构与神经元网络本构[14]。物理基本构有明确的物理参数,但是确定这些参数十分困难,因而应用受到限制[15]。神经元网络本构局限于计算机程序处理,并不获得易用的模型,因而存在局限性。Arrhenius唯象学本构模型具有精度高和易于使用的特点,因而具有实际意义。同时,其特征值(应力指数与变形激活能)可以用来判定高温变形机理,具有理论价值[16,17]。本构建模一般采用热压缩[18,19]、热扭转[20]和热拉伸[21]几种方法。在Mg-Li合金中,采用热压缩方法,Shalbafi等[22]获得了Mg-10Li-1Zn合金的本构模型与加工图;Liu等[23]和Xu等[24]获得了Mg-9Li-3Al合金的流动应力曲线与本构模型;Li等[25]采用神经元网络方法研究了Mg-4Li-3Al合金的本构关系。这些研究者均采用热压缩方法建立本构模型,但尚无采用热拉伸建立Mg-Li合金本构模型的报道。
综上,本工作设计并采用MDFR方法制备了航天器用新型超轻Mg-Li-Zn-Al-Y合金板材;对MDF晶粒细化机理、MDFR成形的α(Mg)基Mg-Li-Zn-Al-Y合金的高温变形流动应力与组织演变、组织演变中的新现象及组织与性能的关系进行研究;采用热拉伸方法在MDFR 制备的Mg-Li-Zn-Al-Y合金中建立本构关系;把位错变量引入Arrhenius唯象学本构,建立位错变量与本构模型之间新的联系,并根据该本构模型定量计算分析其高温变形机理,以期对改善α(Mg)基Mg-Li-Zn-Al-Y合金的成形性与揭示高温变形机理提供理论依据。
实验所用原料为纯度大于99.9%的Mg、Li、Al和Zn,按照设计的成分(Mg-4Li-3Zn-0.5Al-1Y,质量分数,%,下同),采用Jackson方法制备合金铸锭,Y元素以中间合金Mg-30Y 加入。经分析,铸锭的具体化学成分为:Li 4.4,Zn 2.5,Al 0.46,Y 0.74,Mg余量,从而得到Mg-4.4Li-2.5Zn-0.46Al-0.74Y (LZAY-4301)合金。将制备好的铸锭在573 K均匀化后,铣去铸锭表面缺陷,加工成尺寸为40 mm × 30 mm × 22 mm的锻造试块,在2 kN压力机上进行多向锻造[12,13],每一道次压下锻造之后,翻转90°继续锻造,锻造3个道次为1个循环,道次应变为0.5,各道次加热温度依次为1~3道次:648 K、4~9道次:623 K,实现降温锻造。每道次锻造之后水淬到室温,以保留热锻组织。将锻造后的试块在573 K加热1 h,进行热轧与冷轧得到2 mm厚的薄板,热轧总压下率和冷轧压下率分别为82%和50%。将冷轧薄板在523 K退火1 h,随后取样进行力学性能测试。
高温拉伸试样从轧制板材上获取,试样的拉伸方向平行于轧制方向。拉伸试样标距部分尺寸为10 mm × 6 mm × 2 mm。在配有加热和保温电炉的SANS-CMT51054电子拉伸机上进行恒速率拉伸实验。试样在473~623 K保温15 min后在初始应变速率1.67 × 10-2~1.67 × 10-4 s-1条件下以恒定速率拉伸。拉伸后试样立即水淬以保持变形组织。
光学显微分析试样经砂纸水磨和抛光,抛光后用酒精清洗,吹风机吹干,然后采用苦味酸溶液腐蚀。腐蚀液配比为5 mL CH3COOH + 6 g C6H3N3O + 10 mL H2O + 100 mL C2H6O。在DSX500 光学显微镜(OM)上观察金相组织,根据截线法使用IPP软件测定晶粒尺寸。用砂纸把试样表面打磨光滑,利用PW3040-60 X射线衍射仪(XRD)进行物相分析,扫描角度10°~90°,扫描速率为4°/min,电流为40 mA,电压为40 kV。
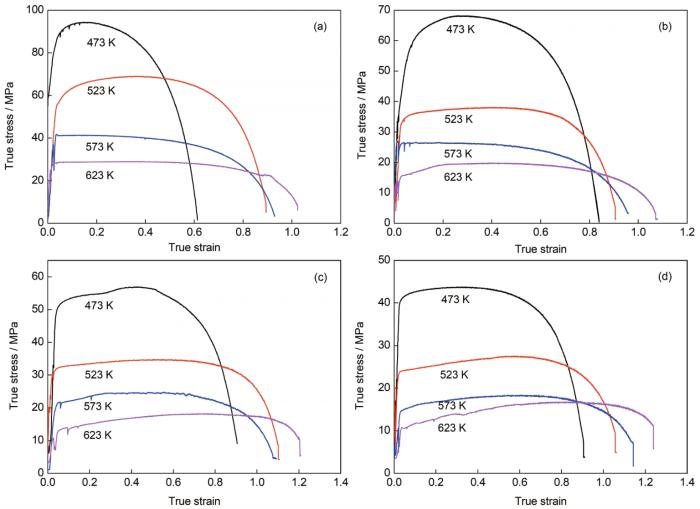
图1为相同应变速率不同温度下LZAY4301合金的真应力-真应变曲线。可以看出,温度与应变速率对峰值应力产生显著影响。一方面,在相同应变速率下,随温度升高,合金峰值应力降低。这是由于温度升高,变形热激活增加,原子扩散加速,位错密度降低,从而引起应力降低。另一方面,在相同温度下,随应变速率降低,合金峰值应力减小。这是由于应变速率降低,合金变形时间延长,热激活和扩散加速,位错密度降低,从而引起应力降低。同时,流动应力起初随应变迅速增加,发生位错增殖,引起应变硬化。到达峰值应力后,硬化与软化达到平衡。继续变形,软化超过硬化,发生动态再结晶,出现流动应力下降(图1a和b)。但是,在523~623 K,随温度增加和应变速率降低,合金硬化阶段明显延长(图1c和d)。从图1d可以看出,LZAY4301合金在温度623 K、应变速率为1.67 × 10-4 s-1条件下获得最大的真应变(1.224)。此真应变对应的最大延伸率为240.0%,表现出类超塑性行为。
图1 相同应变速率不同温度下Mg-4.4Li-2.5Zn-0.46Al-0.74Y (LZAY4301)合金的真应力-真应变曲线
Fig.1 The true stress-true strain curves of Mg-4.4Li-2.5Zn-0.46Al-0.74Y (LZAY4301) alloy at different temperatures and strain rates of 1.67 × 10-2 s-1 (a), 1.67 × 10-3 s-1 (b), 5.0 × 10-4 s-1 (c), and 1.67 × 10-4 s-1 (d)
图2为LZAY4301合金高温变形前的显微组织。由图2a可见,铸态组织基体为hcp结构的α(Mg)固溶体相,晶粒平均尺寸为153 μm。由于内部水冷铜模冷却速率快,铸态组织存在柱状晶。图2b为MDF 1道次的合金组织。可见,α(Mg)相晶粒在垂直压应力的作用下沿水平方向以及其他取向发生变形,表明发生了机械应力作用下的晶粒剪切;同时,在原始的晶界处出现细小的动态再结晶(DRX)晶粒,其平均尺寸为3.9 μm;个别晶粒未发生变化。可见,1道次的合金组织为原始晶粒、机械式剪切晶粒和动态再结晶晶粒共存,平均晶粒尺寸为28.91 μm。图2c为MDF 3道次的合金组织。可见,DRX晶粒数量增多,部分区域出现项链(necklace)式细小晶粒,同时存在伸长、非等轴的粗晶粒;由于外载荷方向变化,造成不同变形区域的晶粒发生相互交割,引起晶粒进一步细化,平均晶粒尺寸为21.50 μm。图2d为多向锻造6道次的合金组织。与3道次组织相比,晶粒等轴化程度明显提高,以细小晶粒为主,但是个别非等轴粗大晶粒依然存在,表现出双峰组织的特征,平均晶粒尺寸为17.68 μm。图2e为轧制板材纵向的组织。可见,在垂直轧制力的作用下晶粒破碎,可观察到沿水平轧制方向的轧制痕迹;经过MDF和轧制,平均晶粒尺寸为8.60 μm。图2f为轧制板材523 K、1.25 h退火的组织。由于发生静态再结晶,晶粒基本等轴化,平均晶粒尺寸为17.54 μm。Langdon[26]和Kawasaki等[27]认为,粗晶(晶粒尺寸大于10 μm)固溶体合金高温拉伸变形通常获得200%~300%的类超塑性;细晶(晶粒尺寸小于10 μm)合金高温拉伸变形通常获得大于400%的真实超塑性,细晶合金可以通过热机械化处理或粗晶高温拉伸发生动态再结晶获得。热拉伸前粗晶组织的存在预示着合金热拉伸将发生类超塑性现象,这与实验中测得的最大延伸率(240%)一致。
图2 LZAY4301合金高温变形前的显微组织
Fig.2 Microstructures of as-cast (a), MDF 1st pass (b), MDF 3rd pass (c), MDF 6th pass (d), cold-rolled along longitudinal direction (e), and annealed and held at 523 K for 1.25 h (f) in LZAY4301 alloy before high-temperature deformation (MDF—multi-directional forging, DRX—dynamic recrystallization)
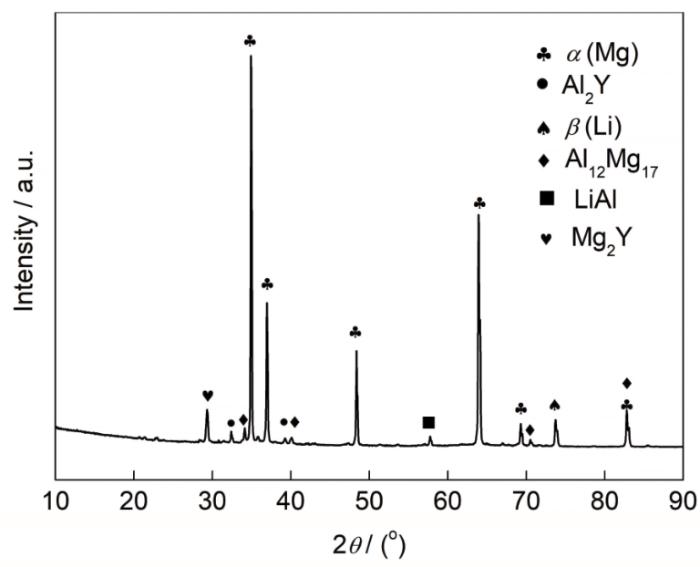
图3是LZAY4301合金退火态的XRD谱。经标定,组织中存在α(Mg)、Al2Y、β(Li)、Al12Mg17、LiAl和Mg2Y相。其中,α(Mg)和β(Li)以固溶体相形式存在,而Al2Y、Al12Mg17、LiAl和Mg2Y相以金属间化合物形式存在。按照Mg-Li平衡相图,Mg-4.4Li合金组成相为α(Mg)固溶体相,没有β(Li)固溶体相。造成LZAY4301合金β(Li)固溶体相出现的原因与铸造时的不平衡凝固有关。Zn元素与Mg元素同属hcp结构,Zn在Mg中的固溶度大,作为溶质固溶到基体Mg中,没有形成第二相。
图3 LZAY4301合金退火态的XRD谱
Fig.3 XRD spectrum of LZAY4301 alloy annealed at 523 K for 1h
图4为523~623 K不同应变速率下LZAY4301合金标距部位的显微组织。表1为对应条件下LZAY4301合金的晶粒尺寸与延伸率。由图4a1~a4可见,在523 K下,与轧制板材在523 K、1.25 h热处理试样(图2f)相比,在应变速率较高时(图4a1和a2),变形部位的晶粒尺寸变化不大,说明在高应变速率下发生了动态回复;而在5.00 × 10-4和1.67 × 10-4 s-1应变速率条件下(图4a3和a4),变形部分的晶粒尺寸减小,说明该温度下以这2个速率拉伸过程中有动态再结晶发生。与图4a1和a2相比,在5.00 × 10-4 s-1速率下,基本为等轴的动态再结晶晶粒,发生动态再结晶充分,晶粒呈网状均匀分布(图4a3)。1.67 × 10-4 s-1条件下,动态再结晶更加充分,并伴随少量晶粒长大(图4a4)。
图4 523~623 K不同应变速率下LZAY4301合金标距部位的OM像
Fig.4 OM images of gauge section in LZAY4301 alloy after high-temperature deformation at temperatures of 523 K (a1-a4), 573 K (b1-b4), and 623 K (c1-c4), and strain rates of 1.67 × 10-2 s-1 (a1-c1), 1.67 × 10-3 s-1 (a2-c2), 5.00 × 10-4 s-1 (a3-c3), and 1.67 × 10-4 s-1 (a4-c4)
表1 523~623 K不同应变速率下LZAY4301合金的晶粒尺寸与延伸率
Table 1
Temperature
K
Strain rate
s-1
Grain size
μm
Elongation
%
由图4b1~b4可见,在573 K下,应变速率为1.67 × 10-2 s-1时,由于应变速率高、变形时间很短,晶粒发生动态回复(图4b1);但是随着应变速率的降低(1.67 × 10-3 s-1),动态再结晶充分,个别晶粒发生少量长大,晶粒的平均尺寸已经达到21.23 μm (图4b2);当应变速率为5.00 × 10-4 s-1时,动态再结晶充分,同时伴随晶粒长大,平均晶粒尺寸达到27.64 μm (图4b3);当应变速率为1.67 × 10-4 s-1时,晶粒的尺寸变大,伸长晶粒出现,表明此时除了晶界滑移外还发生晶内滑移,平均晶粒尺寸达到29.33 μm (图4b4),这主要是因为低应变速率下有充分的时间发生连续的动态再结晶,同时晶粒也有足够的时间发生扩散和晶界迁移,引起晶粒长大。
由图4c1~c4可见,在623 K下,拉伸后晶粒尺寸整体比较粗大,说明晶粒在经过动态再结晶后迅速长大,出现晶粒的吞并现象,但是图4c1和c2的晶粒基本等轴化,而图4c3和c4的晶粒沿水平方向伸长,表明除了晶界滑移外还发生晶内滑移。与573 K相比,同样的应变速率下,623 K时的晶粒更加粗大,而且晶粒长大也更加迅速。这主要是因为温度更高,原子扩散也更加剧烈,晶界迁移的速率随之加快。
一定应变下,反映流动应力与温度、应变速率关系的Arrhenius本构方程由下式给出[28,29]:
式中,Z为Zener-Hollomon参数[30];
为了确定材料常数与激活能,将
图5为高温拉伸条件下LZAY 4301合金的ln
图5 高温拉伸条件下LZAY4301合金的ln
Fig.5 Curves of ln
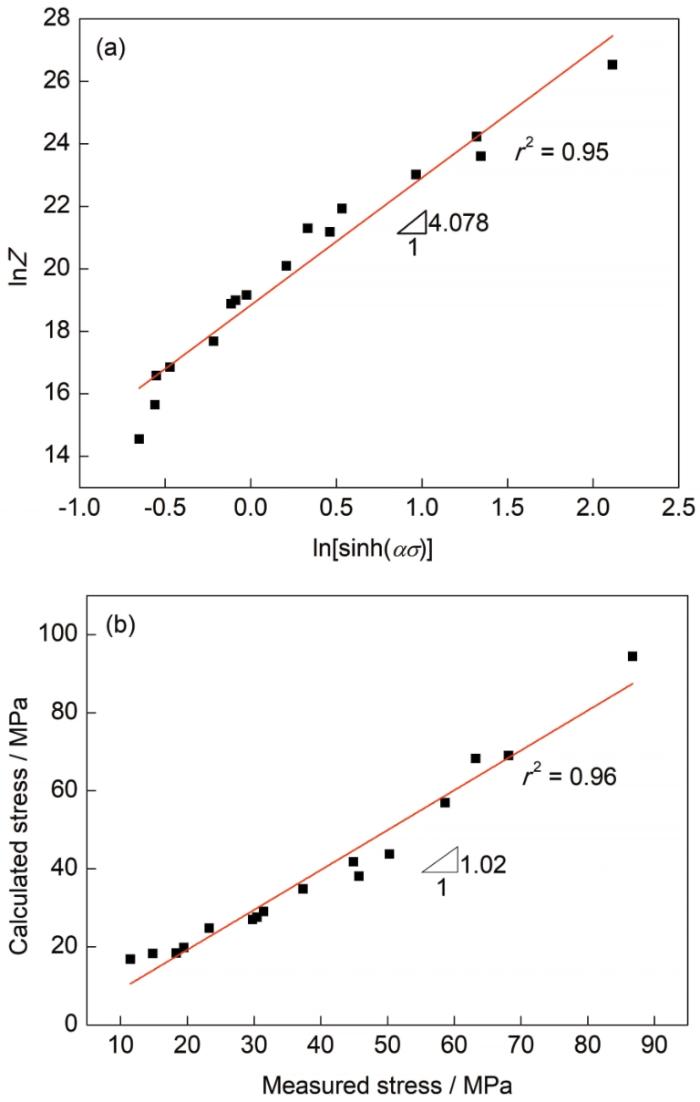
图6为lnZ-ln[sinh(ασ)]关系曲线以及计算应力与测量应力的比较。由图6a可得,曲线横坐标为0时的lnZ值为lnA,lnA = 18.83,从而获得A = 1.506 × 108。根据曲线斜率n = 4.078,相关系数r2 = 0.95,得到LZAY4301合金双曲正弦本构方程:
图6 lnZ-ln[sinh(ασ)]关系曲线以及计算应力与测量应力的比较
Fig.6 Relation curve of lnZ-ln[sinh(ασ)] (a), and comparison of calculated stress and measured stress (b) (Z—Zener-Hollomon parameter, r2—related coefficient)
因此,得到Z参数表达的应力如下:
如图6b所示,计算应力与测量应力的相关系数r2 = 0.96,误差在合理的范围之内。
在本文作者[32]以前的工作中, 分别建立了位错密度和位错数量与本构方程Z参数之间的关系式:
式中,ρ为位错密度,C为无量纲常数,G为剪切模量,b为Burgers矢量模,N为单个晶粒内部产生位错的数量,ν为Poisson比,d为线截距晶粒尺寸。但是在文献[32]中并没有用该模型计算位错密度和位错数量,因此在本工作中做具体计算,揭示变形机理。
为了模型计算而收集下列数据。G由下式给出[33]:
根据
623 K热拉伸峰值计算应力F(Z)产生误差的原因在于,该温度下合金拉伸过程中发生动态晶粒长大引起的组织失稳;由于存在组织失稳,流动应力曲线形状发生变化,引起计算的误差。
如图2b~d所示,由于锻造过程中垂直压应力转化为变形体内部剪切应力,MDF第1道次组织在外力作用下发生晶粒切割,晶粒呈现与垂直压应力成一定角度的排列,这表明发生机械式剪切应力诱发的晶粒破碎。MDF第3道次,项链式(necklace type)细化的晶粒出现,表明合金发生不连续动态再结晶。MDF第6道次,晶粒基本等轴化。经过2个循环的应力轴线不断变化,MDF合金组织不断发生相互剪切交割,引起晶粒细化,同时高温MDF发生动态再结晶晶粒细化。锻造变形外应力作用下会引起变形体内部的剪切应力,该剪切应力引起晶粒交割细化。因此,LZAY4301合金MDF晶粒细化机理为机械式剪切破碎与动态再结晶细化。MDF之后的轧制过程合金发生常规轧制晶粒细化,不再赘述。MDFR过程应变不断累积,累积应变不断增加,引起晶粒逐步细化。
根据图2和3,LZAY4301合金是α(Mg)为基体相并含有少量第二相的准单相合金。准单相合金的MDF晶粒演变机理与双相合金的MDF晶粒细化机理存在一定差别。Shah等[36]研究准单相Mg-Gd-Y合金锤锻MDF演变认为,晶粒细化机理是孪晶细化和连续与不连续动态再结晶。张阳等[37]研究准单相Mg-5.6Gd-0.8Zn合金MDF机制发现,孪晶与扭折变形和动态再结晶是其晶粒细化机理。准单相LZAY4301合金MDF晶粒细化机理与上述作者提出的机理存在差别,没有孪晶与扭折,而是显著的机械式剪切破碎与动态再结晶联合细化。本文作者等[12,13]在MDF双相Mg-10.2Li-2.1Al-2.23Zn-0.2Sr合金的研究中发现,软β(Li)相协调硬α(Mg)相变形,α(Mg)相发生不完全动态再结晶;并在MDF双相Mg-6.4Li-3.6Zn-0.37Al-0.36Y合金的研究中发现,β(Li)相发生变形诱发动态再结晶,而α(Mg)相发生比较弱的机械式破碎细化与变形诱发原位动态再结晶细化。准单相LZAY4301合金由于硬相α(Mg)占主导,发生强烈的机械式剪切破碎晶粒细化以及发生明显的不连续动态再结晶细化。上述结果反映出合金成分与相组成对细化机理的影响。随Li含量增加(4.4Li→6.4Li→10.2Li),合金β(Li)含量逐渐增多,α(Mg)相含量逐渐减少。合金β(Li)相调节α(Mg)相变形的能力增强,α(Mg)相机械式剪切破碎晶粒细化由强变弱,甚至出现不完全动态再结晶或部分动态再结晶的组织。而这些MDF镁合金的共同特点是动态再结晶晶粒细化,这与Mg的层错能低有关。
首先,动态再结晶合金流动应力曲线通常表现为3个阶段:峰值应力前的初始应变硬化阶段、峰值应力后流动软化阶段和硬化与软化达到平衡的稳态流动阶段。Kim和Kwak等[38]研究Mg-9.5Zn-2.0Y热压缩变形行为认为,镁合金随着动态再结晶的不断进行,未必一定达到稳态。LZAY4301合金热拉伸流动应力曲线的突出特点是没有稳态流动阶段,而是表现出峰值应力前的初始应变硬化阶段和峰值应力后的流动软化阶段。这与粗晶组织存在的位错滑移变形有关。与室温变形相比,高温变形激活晶粒更多的滑移系,不仅发生基面滑移而且发生非基面滑移,晶内滑移引起的晶界应力集中使合金较快地出现缩颈失稳,引起过早断裂,因此,合金始终没有出现硬化与软化达到平衡的稳态流动阶段。其次,LZAY4301合金在高温低速下的流动应力发生很长的应变硬化阶段,这与组织发生的晶粒长大一致。高温低速下,热激活与原子扩散加快,晶界迁移引起α(Mg)相晶粒长大,α(Mg)相高温变形的“惰性”增强,变形阻力增加,从而造成很长的应变硬化阶段。第三,合金中第二相对组织稳定性和流动应力的影响与特定变形温度有关。合金中第二相的熔点分别为1758 K (Al2Y)、728 K (Al12Mg17)、熔点数据未知 (LiAl)和1053 K (Mg2Y)[39]。熔点较高的第二相对合金室温强化起重要作用,高温下会通过颗粒诱发形核(PSN)诱发不连续动态再结晶(图2c)。然而,由于Al和 Y等元素含量少,合金抑制晶粒长大的能力表现为:在低于573 K下组织稳定,高于此温度组织不稳定。LZAY4301合金在热变形温度523~573 K时组织相对稳定,流动应力存在一定的水平阶段和下降软化阶段,表明主要发生动态回复与动态再结晶;高于573 K (含573 K)低应变速率下流动应力出现应变硬化阶段,表明热变形组织不稳定,发生晶粒长大。
在2.3节本构分析中,获得n = 4.4和Q = 120.40 kJ/mol,接近晶格扩散激活能(134.84 kJ/mol),表明位错蠕变是合金主导的变形机理。由于合金高温变形过程是热激活过程,原子扩散必然发生,因此,有必要确定扩散机理。扩散包括晶界扩散、位错管(芯)扩散和晶格扩散等扩散形式。相应地,存在晶界扩散系数(Dgb)、位错管(芯)扩散系数(Dp)和晶格扩散系数(DL)等数据。Somekawa等[40]提出如下形式的归一化应力判定扩散的模型:
式中,(σ / G)cri为临界归一化应力;β1为常数,β1 = 7.4;DL(α) = 10-4exp(-QL(α) / (RT)) (其中,根据固溶体晶格扩散激活能(QL(α))线性模型[41],QL(α) = QL(Mg)·[Tm(α) / Tm(Mg)],式中,QL (Mg)为Mg晶格扩散激活能,Tm(α)为α固溶体熔点,Tm(Mg)为Mg熔点);Dp = Dgb = 10-4exp(-Qgb / (RT)) (其中,Qgb = 6.93RTm(α),0.22 < T / Tm(α) < 0.42;Qgb = 9.35RTm(α),0.42 < T /
Tm(α) < 1.0[42,43])。如果σ / G < (σ / G)cri,则管扩散机理占主导;如果σ / G > (σ / G)cri,则晶格扩散机理占主导;如果σ / G = (σ / G)cri,则管扩散机理和晶格扩散机理各占一半。
在T = 623 K、初始应变速率1.67 × 10-4 s-1条件下,σ = 16.82 MPa (图1)。QL(Mg) = 134.84 kJ/mol[31]。根据相图[44],确定Tm(α) = 893 K,Tm(Mg) = 923 K。从而得到DL(α) = 1.15 × 10-15 m2/s,Dp(α) = 1.51 × 10-10 m2/s,G = 13756.62 MPa。计算得σ / G = 1.22 × 10-3,(σ / G)cri = 1.01 × 10-3,表明晶格扩散为主要的扩散机理。考虑到特征值n和Q,断定合金在623 K,1.67 × 10-4 s-1条件下的变形机理为晶格扩散控制的位错蠕变。
623 K、1.67 × 10-4 s-1条件下的晶粒长大包括静态晶粒长大和动态晶粒长大。静态晶粒长大是未加应变的退火过程,而动态晶粒长大是施加应变的退火过程。单相合金静态晶粒长大模型如下[45]:
式中,d'为t时间后静态退火晶粒尺寸;d0为t = 0时静态退火晶粒尺寸;γ为晶界表面张力;Ω为原子体积;W为晶界宽度,W = 2b;k为Boltzmann常数;K为长大速率因子。
超塑性动态晶粒长大模型如下[46]:
式中,D为在真应变ε热拉伸后的晶粒尺寸;D0为热拉伸开始的晶粒尺寸;α'为比例因子;q为晶粒长大指数,这里q = 2;
确定T = 623 K,
(1) 制造了超轻Mg-4.4Li-2.5Zn-0.46Al-0.74Y合金板材,合金多向锻造晶粒细化机理为机械式剪切破碎与动态再结晶细化。退火后晶粒尺寸为17.54 μm的粗晶合金在623 K、1.67 × 10-4 s-1条件下获得了240%的延伸率,表现为类超塑性。
(2) 流动应力实验结果表明,合金在623 K发生晶粒长大引起的应变硬化。显微组织观察表明,粗晶合金在热变形温度523~573 K时主要发生动态回复与动态再结晶;≥ 573 K时热变形组织主要发生晶粒长大。XRD分析表明,合金退火组织组成相为α(Mg)、β(Li)、Al2Y、Al12Mg17、LiAl和Mg2Y相。
(3) 采用包含位错变量的本构模型,计算获得了应力指数为4.4,变形激活能为120.40 kJ/mol;位错密度和数量与原子扩散计算表明,合金在623 K、1.67 × 10-4 s-1条件下的变形机理为晶格扩散控制的位错蠕变。晶粒长大模型确定该条件下的晶粒长大指数q = 2,比例因子α' = 0.2。
1 实验方法
1.1 合金制备
1.2 力学性能测试
1.3 显微组织表征
2 实验结果
2.1 高温变形流动应力曲线
图1
2.2 显微组织
2.2.1 合金高温变形前的显微组织
图2
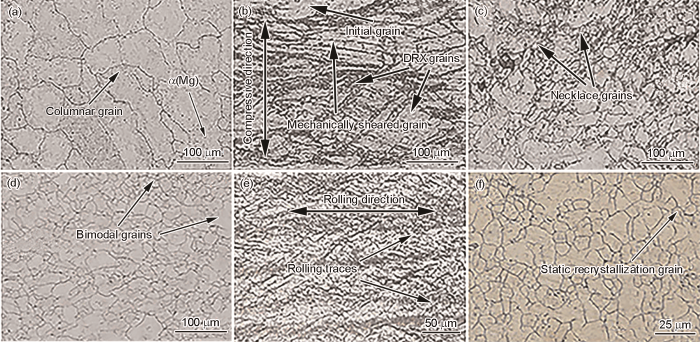
图3
2.2.2 合金高温变形后的显微组织
图4

523
1.67 × 10-2
17.78
144.6
1.67 × 10-3
17.92
147.9
5.00 × 10-4
16.39
202.2
1.67 × 10-4
17.19
189.3
573
1.67 × 10-2
17.59
153.4
1.67 × 10-3
21.23
160.8
5.00 × 10-4
27.64
197.9
1.67 × 10-4
29.33
213.5
623
1.67 × 10-2
23.07
178.3
1.67 × 10-3
29.74
193.8
5.00 × 10-4
32.97
235.0
1.67 × 10-4
34.48
240.0
2.3 本构分析
图5
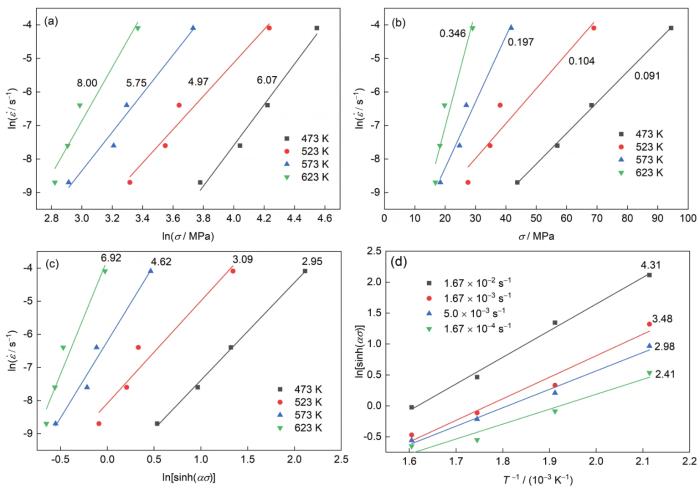
图6
3 分析讨论
3.1 MDFR晶粒细化机理
3.2 高温变形流动应力与显微组织的关系
3.3 高温变形机理分析
3.4 合金晶粒长大模型分析
4 结论
来源--金属学报







 沪公网安备31011202020290号
沪公网安备31011202020290号
