陈翔1,2,3, 陈伟1, 赵洋1, 禄盛1,3, 金晓清2, 彭向和 ,2
,2
1. 重庆邮电大学先进制造工程学院 重庆 400065
2. 重庆大学机械传动国家重点实验室 重庆 400044
3. 西安交通大学机械结构强度与振动国家重点实验室 西安 710049
摘要
基于考虑塑性变形和相变耦合效应的记忆合金(SMA)本构模型,对NiTiNb SMA管接头从扩径预处理到装配服役的全过程以及拉拔过程进行数值模拟。计算结果表明,由于相变和塑性变形的耦合作用,装配过程管接头内的von Mises应力、等效相变应变和等效塑性变形演化存在明显的规律。在一定尺寸范围内,随着扩径量的增加,拉拔力降低;不同壁厚尺寸配比的9种方案中,拉拔力随壁厚非线性变化,存在最优连接性能的方案;在室温变化范围内(0~40 ℃),服役环境温度对管接头连接系统的性能影响较小。随着临界相变应变的增加,管接头内的von Mises应力集中层由内侧向外侧移动,拉拔力在临界相变应变0.07~0.14的范围内逐渐增加。研究结果表明,接触时端部von Mises应力集中会显著增加系统的拉拔力。
关键词: 形状记忆合金 ; 管接头 ; 相变 ; 塑性变形 ; 拉拔力
管接头是管道连接工程的基本组成部分,广泛应用于流体输运各领域。基于形状记忆合金(shape memory alloy,SMA)制备的管接头,具有结构简单、易于装配和连接可靠性高等特点,目前已广泛应用于航空、运输和石油化工等行业[1,2,3]。例如,采用SMA制作的管接头被应用于军用飞机输油管道的连接超过140万次[4],目前为止无一失效,由此可见其服役的高可靠性。在现有的SMA材料中,NiTi二元合金表现出优异的伪弹性(pseudoelastic,PE)和形状记忆效应(shape memory effect,SME) (大约8%的可恢复应变)。与传统的NiTi二元合金(温度滞后区间约30 ℃)相比,NiTiNb形状记忆合金具有良好的延展性、耐腐蚀性以及较宽的温度滞后特性(约150 ℃)[5],利用该合金制成的SMA管接头,克服了传统SMA管接头必须低温储存、运输和装配的缺陷,可以实现在常温下储存和安装,大大降低其服役成本[6,7,8]。
截至目前,研究者们对SMA本构模型进行了大量研究[9,10,11,12,13,14],提出了SMA细观力学模型和三维唯象本构模型。上述模型多针对NiTi SMA,且限定在弹性-相变阶段,未引入塑性变形的影响。而对于NiTiNb SMA 管接头,装配前引入一定量的塑性变形以在常温下获得稳定马氏体是其显著特点。因此,对NiTiNb SMA管接头相关研究需考虑塑性变形的影响。Brinson[15]利用有限元分析方法研究了塑性应变对双向形状记忆效应的影响。Jiang等[16]发现,基于等通道角挤压的严重塑性变形对增强Ni47Ti44Nb9 (原子分数,%)形状记忆合金的转换迟滞起着重要作用。Uchida等[17]发现TiNiNb合金的恢复von Mises应力随着预应变的增加而增加,在预应变为9%时,其最大恢复von Mises应力达到最大值450~500 MPa之后开始下降。
鉴于NiTiNb本构模型的复杂性,对NiTiNb本构模型的研究相对较少[9,17,18,19],且在国内外基于SMA本构模型的管接头-管道连接系统优化和数值仿真的报道中[20,21,22,23,24,25,26,27,28],尚未考虑塑性变形及其影响。例如徐祥等[21]和康泽天等[22]基于热力学自由应变能,研究了NiTi合金管接头系统的整体力学行为。马彦和李威[23]建立了NiTiNb形状记忆合金管接头结构优化模型,并利用遗传算法进行分析。智友海等[24]基于马氏体相变晶格理论,研究了不同边界和载荷条件对管接头系统的影响。张慧博等[25]和尹向前等[26]从建立本构方程计算模型出发,对影响TiNiNb管接头连接过程中径向应力的因素进行了研究。Piotrowski等[20]、张慧博等[27]和陈强等[28]研究了内脊对形状记忆合金管接头系统拉拔力的影响。管接头预变形扩孔时由于变形的梯度效应,会在靠近内表面处产生显著的塑性变形,这会影响逆向相变的恢复,同时改变管接头内应力场的分布。因此,为了更加精细地模拟管接头装配服役性能,需系统研究装配服役过程中塑性变形对其力学性能的影响。
鉴于此,本工作在课题组所建立的考虑塑性变形和相变耦合的SMA本构模型基础上[29],构建一种考虑形状记忆合金塑性变形-相变耦合效应的SMA管接头-钢材管道系统(joint-steel pipe,简称J-P系统)连接装配方案,开展不同扩径量、不同壁厚、不同使役温度以及不同临界相变应变的SMA J-P系统装配服役工况下的管接头von Mises应力分布、接触压力分布和拉拔力的数值仿真分析,找出拉拔力及与其直接相关的力学参量(von Mises应力、接触压力等)随NiTiNb J-P系统的外径尺寸、拉拔温度和临界相变应变等的变化关系,探索塑性变形和相变耦合作用对管接头装配服役性能的影响规律。
1 本构模型
对于NiTiNb形状记忆合金,其本构模型简单回顾如下[29]。取温度(T)、总应变(ε)和一组内变量为状态变量,根据形状记忆合金的一般特性并考虑塑性变形的影响,将内变量分为2组,分别描述相变和塑性变形对应的耗散,包含相变应变(εt),塑性应变(εp)、运动强化变量(α)和等向强化变量(p)。
假设存在一个热力学自由能势函数Φ,耗散材料的热力学状态可由T、ε及内变量(εt、εp、α、p)的一个完整集合唯一决定:
(1)
通常情况下自由能函数可以写成如下形式[30]:
(2)
式中,为热膨胀应变,θ为线性膨胀系数张量,T0为参考温度;为弹性应变,。将Φ进一步分解为弹性、相变、塑性、温度、及相变和塑性变形耦合对应的部分,即
(3)
其中弹性部分:
(4)
相变部分:
(5)
塑性部分:
(6)
温度部分:
(7)
相变和塑性变形耦合部分:
(8)
式中,C为弹性刚度张量;Cp和Ct为材料常数,均为温度相关量,本工作为简化计算,不考虑其随温度的变化;ρ和cv分别是材料的密度和比热容,且假设它们在相变过程中保持不变;Y(p)常用于描述屈服面等向强化[30];表示二阶张量εt的Euclid范数;τM(T)的定义为:
(9)
式中,参数B表示相变的临界应力随温度变化的比例系数;M0为参考温度[31],通常取马氏体相变结束温度(Mf)作为其值。Γ(εt)和εt受如下约束:
(10)
这表示相变应变存在最大值,γ为Lagrange乘子;εL表示相变达到饱和时的最大相变应变,即临界相变应变。函数Q(p)通过背应力间接影响相变发生的条件,本工作定义Q(p)=Q0(1-exp(-ξp))以描述塑性变形与其引起的逆相变开始温度(As)提高间的关系,式中Q0和ξ分别为材料参数。定义耗散势函数:
(11)(12)
分别用于获得相变和塑性变形内变量的演化。式中,a为材料常数,σ为应力,χt为相变背应力,χp为塑性变形背应力,R为塑性变形部分的曳应力,f t(σ, χt, T)和f p(σ, χp, R, T)分别为相变和塑性变形的屈服函数。通过对式(3)全微分可获得内变量演化方程组。运用图形返回法迭代求解各内变量并编译用户自定义子程序(UMAT),导入到ABAQUS材料库中进行数值分析。
2 J-P系统有限元模型
NiTiNb SMA J-P系统2D模型如图1所示,对应3D模型尺寸列于表1中。为更好地反映实际装配过程中von Mises应力、相变应变和塑性变形等力学参数的变化情况,将2D模型提升至3D模型,进行有限元仿真计算。NiTiNb SMA管接头的扩孔、升温等装配过程是轴对称问题[32],为节约计算资源,采用整体结构的1/4模型表示(将2D模型沿对称轴周向旋转90°),如图2所示,并施加轴对称边界条件进行约束,以NiTiNb SMA管接头壁厚的16%作为位移扩张量进行扩孔。因被连接管外表面与NiTiNb SMA管接头内表面在装配过程以及拉拔过程是面接触形式,故添加切向行为的“罚”接触对形式。因被连接管的弹性模量大于NiTiNb SMA管接头中,故将被连接管外表面定义为主动接触面,NiTiNb SMA管接头内表面定义为从动接触面,摩擦系数设置为0.2[15]。
图1

图1 NiTiNb管接头-钢材管道(J-P)系统2D模型
Fig.1 2D model of NiTiNb joint-steel pipe line (J-P) system (SMA—shape memory alloy)
表1 NiTiNb SMA J-P系统3D模型尺寸 (mm)
Table 1 Size parameters of 3D model of NiTiNb SMA J-P system (mm)
|
Material
|
L
|
r
|
W
|
H
|
|
NiTiNb SMA joint
|
11.00
|
3.00
|
5.00
|
1.00
|
|
Connected pipe
|
7.50
|
2.00
|
3.22
|
0.61
|
Note: L—length; r—internal diameter; W—outer diameter; H—thickness
新窗口打开| 下载CSV
图2

图2 NiTiNb J-P系统有限元3D模型及剖视图
Fig.2 3D finite element model (a) and sectional view (b) of NiTiNb J-P system (pick point—point used to observe the stress-strain curve, rP—internal diameter of contacted pipe, WP—outer diameter of contacted pipe, LP—length of contacted pipe, rJ—internal diameter of SMA joint, WJ—outer diameter of SMA joint, LJ—length of SMA joint)
Color online
NiTiNb SMA材料本构模型采用陈翔等[29]构建的考虑塑性变形和相变耦合效应的三维唯象学本构模型,该模型数值模拟的有效性已经被实验验证。被连接管采用ABAQUS自带的弹塑性模型。管接头和被连接管均采用八结点线性六面体单元(C3D8)。NiTiNb SMA管接头及被连接管的数值仿真参数参见文献[29]。为加快计算收敛,可采取如下设置技巧,将NiTiNb SMA管接头和被连接管的接触面网格单元对齐(单元节点重合),且整体单元网格数不必太多(2000~3000个网格即可,网格数太多会导致计算迭代次数过多,从而增加收敛难度),最大增量时间步长设置为0.001。这一设置不会对计算精度产生影响。
3 J-P系统装配过程
通常情况下,NiTiNb SMA在(Ms+30) ℃ (Ms为奥氏体转变为马氏体的起始温度)下预变形16%时可以显著提高其逆向相变滞后温度并保持较高恢复率[33]。本工作模拟的NiTiNb合金的Ms=-90.37 ℃,逆相变结束温度Af =-15.75 ℃[34],因此将模拟的预变形温度设定在-60 ℃。实验结果表明,当温度升高到100 ℃时,合金逆向相变已基本完成。因此,将NiTiNb合金相变温度参数设定为实验温度,模拟温度范围取-60~100 ℃。NiTiNb J-P系统的装配及拉拔过程以温度为自变量,分5个步骤进行,如图3a所示。第1步:NiTiNb SMA管接头在-60 ℃下扩孔到预设变形量;第2步:保持温度-60 ℃不变,移除载荷后将被连接管装配到完成扩径的NiTiNb SMA管接头中;第3步:温度缓慢升至100 ℃,NiTiNb SMA管接头发生温度诱发的逆向马氏体相变,管接头孔径恢复从而与被连接管产生紧密的接触作用;第4步:温度降至服役温度(取室温23 ℃),计算其常温下的接触作用;第5步:将被连接管从NiTiNb SMA管接头中拔出,以获得服役过程J-P系统的连接性能。通过上述步骤实现对NiTiNb SMA管接头和被连接管整个装配过程以及拉拔性能的数值模拟。
图3
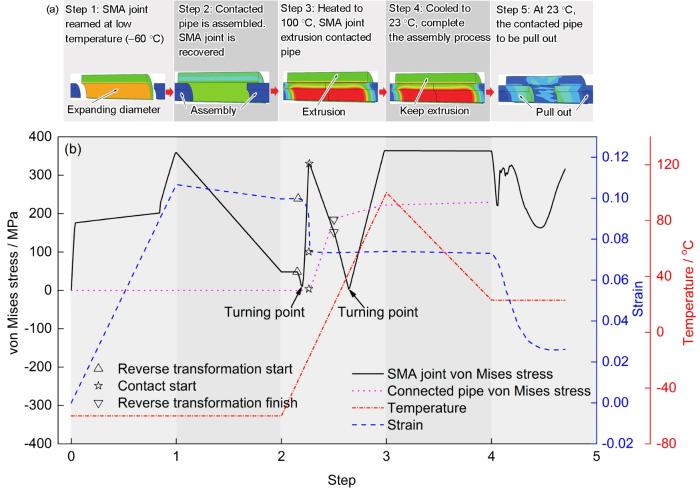
图3 装配及拉拔过程示意图以及各阶段不同变量的变化关系曲线
Fig.3 Schematics of assembly and pull-out processes (a) and variation curves of variables at different stages (b)
Color online
与上述过程对应,图3b绘制了装配及拉拔过程中NiTiNb SMA管接头内表面的中间点(选取点如图2a所示)的von Mises应力、应变和相应的被连接管外表面点的von Mises应力以及全过程环境温度变化曲线。由图3b可见:
第1步(Steps 0~1):温度保持-60 ℃不变,被连接管外表面无任何外力作用,von Mises应力为0 MPa;SMA管接头选取点的应变随着扩径量的增加而直线上升。马氏体相变临界应力()和塑性临界应力()分别为175和220 MPa[29]。因此,选取点的von Mises应力历经0~175 MPa的弹性阶段、175~200 MPa的相变阶段和200~220 MPa的弹性阶段及220 MPa以上的弹塑形阶段。
第2步(Steps 1~2):温度保持-60 ℃不变,装配被连接管到NiTiNb SMA管接头中间位置,此时尚无其它外力作用,被连接管外表面von Mises应力保持为0 MPa;NiTiNb SMA管接头内表面的扩径载荷已经移除,整个NiTiNb SMA管接头处于自由恢复状态,所以选取点的von Mises应力和应变开始减小,由于相变应变和塑性变形的耦合作用,选取点的von Mises应力无法完全回复,从360 MPa恢复到50 MPa;同理,由于没有发生逆向马氏体相变,此时的NiTiNb SMA管接头内表面变形只有弹性部分的恢复,选取点的应变由10.8%恢复到10%。
第3步(Steps 2~3):温度作为自变量由-60 ℃逐渐升高到100 ℃。此过程中由于相变应变和塑性变形的综合作用,选取点的von Mises应力变化较为复杂,经历了以下5个变化阶段:(1) 保持阶段(50 MPa左右);(2) 下降阶段;(3) 上升阶段;(4) 下降阶段;(5) 上升阶段。为精细分析此加载步von Mises应力变化时对应选取点处的应力状态变化,图4给出了选取点处von Mises应力和环向应力的变化曲线,图5为曲线上特征点(A1~A5、B1~B5)所对应的管接头横截面von Mises应力和环向应力状态分布云图。对比图3,4,5分析可得:
图4
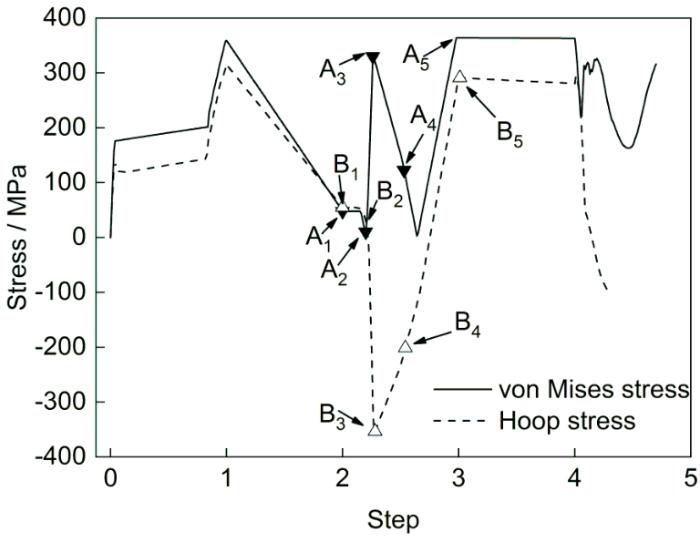
图4 装配过程SMA管接头内选取点的von Mises应力和环向应力变化
Fig.4 von Mises stress and hoop stress changes at selected points in SMA joints during assembly process
图5

图5 装配步骤2到3对应加载点SMA管接头截面上von Mises应力和环向应力分布云图
Fig.5 von Mises stress and hoop stress distributions on cross section of SMA joint at the corresponding loading points A1~A5 (a) and B1~B5 (b) in Fig.4 in assembly steps 2 to 3
Color online
(1) 保持阶段(50 MPa左右):随着温度上升,在未达到逆向马氏体相变临界温度之前,管接头尚未与被连接管接触,管接头处于无相变的自由热膨胀阶段,选取点的von Mises应力保持不变,其环向应力处于拉伸应力状态。
(2) 下降阶段:随着温度的升高,当温度达到逆向马氏体相变临界温度后,发生逆向马氏体相变,逆向相变恢复变形克服塑性变形的作用,此过程应变持续恢复,由于之前产生的塑性变形导致了选取点处于拉伸应力状态,而逆向相变的恢复导致其拉伸部分收缩,其von Mises应力随着温度的升高而降低,其环向应力由拉伸应力状态向压缩应力状态转变。
(3) 上升阶段:随着逆向马氏体相变的进行,选取点处的应变持续恢复,环向应力状态由拉伸应力转变为压缩应力;并随着应变恢复量的增加而逐渐增大,直到与被连接管接触,其压缩应力达到峰值。这一阶段von Mises应力从0 MPa逐渐升高,von Mises应力曲线上的转折点对应于环向应力状态(拉伸↔压缩)的转变。
(4) 下降阶段:开始接触后受被连接管的约束作用,在管接头内表面产生拉伸应力,与管接头内原有的压缩应力相互作用导致总体的von Mises应力持续减小。
(5) 上升阶段:继续升温,相变后由于管接头(10-5 ℃-1)与被连接管(1.2×10-5 ℃-1)热膨胀系数的差异导致选取点处应力状态由压缩应力转变回拉伸应力并逐渐增加,von Mises应力由降转升,升温结束时达到最大值。
选取点的应变历经3个变化过程:(1) 对应于应力保持阶段,由于未发生逆向马氏体相变,主要是热膨胀导致应变小幅增加,其斜率等于其热膨胀系数;(2) 对应于应力下降阶段和上升阶段,这一阶段由逆向马氏体相变和热膨胀共同作用,且逆向相变的应变恢复贡献远大于热膨胀,应变迅速恢复并使管接头与被连接管外表面紧密接触。由于被连接管外表面的阻碍作用,选取点的应变由0.1恢复到0.075左右便停止;(3) 随着温度继续升高,因被连接管外表面的阻碍作用,NiTiNb SMA管接头内表面无法继续回复,其选取点的应变保持在0.075左右。
被连接管选取点的von Mises应力经历了如下3个过程:(1) 随着温度升高,在NiTiNb SMA管接头内表面与被连接管外表面接触之前,被连接管选取点von Mises应力恒为0 MPa;(2) 在开始接触后,由于NiTiNb SMA管接头的逆向相变和热膨胀的共同作用(逆向相变大于膨胀率),使得NiTiNb SMA管接头内表面与被连接管外表面产生紧密接触,被连接管外表面选取点的von Mises应力(压缩状态)急剧上升至190 MPa左右;(3) 此后,管接头内逆向马氏体相变完成,热膨胀再次起主导作用,由于NiTiNb SMA管接头的膨胀系数小于被连接管,继而挤压被连接管,致使被连接管外表面选取点的von Mises应力进一步升高,但上升速率小于前一步。
第4步(Steps 3~4):温度从100 ℃缓慢降至23 ℃,选取点应变随温度的降低而略有降低,选取点的von Mises应力几乎保持不变。
第5步(Steps 4~5):温度保持23 ℃不变,将被连接管从NiTiNb SMA管接头中拔出,可见选取点的应变先是随着拉拔位移(与时间步一致)的增加而急剧降低,后趋于平缓,最后保持在0.028左右,完成整个拉拔过程;这一阶段选取点的应力和被连接管外表面选取点的von Mises应力则随着拉拔的增加而表现出波动性,拉拔过程的应力变化较为复杂。
图6是SMA管接头选取点所处横截面在每个加载步结束时的von Mises应力、等效相变应变和等效塑性应变的分布云图。结合图3可以看出:在第1步结束时,von Mises应力和相变应变达到最大值,并产生一定的塑性应变,3者的分布沿径向呈明显的梯度效应,即由内表面向外表面逐渐减小,沿环向均匀分布;在第2步结束时,因扩径外载被移除,von Mises应力显著恢复,因未达到逆向马氏体相变临界条件,等效相变应变和塑性变形保持不变。在第3步结束时,由于升温诱发逆向马氏体相变,等效相变应变显著减小。逆向相变使NiTiNb SMA管接头内表面变形恢复,与被连接管外表面产生紧密接触,使得von Mises应力上升,塑性变形保持不变。第4步结束时,管接头内的von Mises等效应力基本保持不变,选取点所处的高应力状态以及被连接管外表面的支撑作用,导致SMA管接头内的马氏体无法转变回母相,从而使相变应变继续保持不变;由于管接头内的von Mises等效应力基本保持不变,在该降温步骤中没有新的塑性变形产生,因此等效塑性应变也保持不变,与图3中的结果一致。第5步结束时,因拉拔过程内表面接触区域应力状态较为复杂,靠近内表面von Mises应力有所变化,而靠近外表面的von Mises应力保持不变。这一阶段等效相变应变和等效塑性变形保持不变。
图6

图6 加载步结束时SMA管接头横截面von Mises应力、等效相变应变和等效塑性应变分布云图
Fig.6 Distributions of the von Mises stress (a), equivalent transformation strain (b) and equivalent plastic strain (c) on the cross section of the SMA joint at the end of loading steps
Color online
4 J-P系统装配性能的数值模拟
4.1 扩径量对J-P系统装配性能的影响
在上述装配过程中,NiTiNb SMA管接头在(Ms+30) ℃下进行扩径处理能获得较大的回复率和可恢复变形,不同扩径量(h)下的NiTiNb SMA管接头产生的塑性形变不同,装配完成后的应力场不同,从而使其连接性能产生差异。装配过程中,h太小会导致被连接管无法顺利装配;h过大会使NiTiNb SMA材料产生较大的塑性变形,影响NiTiNb SMA管接头后续的形变恢复量,导致系统抱紧力不够,稳定性不足。为明确扩径量对NiTiNb SMA管接头形变恢复量的影响规律,本工作针对相同NiTiNb J-P系统模型尺寸,开展不同扩径量的管接头von Mises应力和拉拔力的研究。在表1所示尺寸下,将h从0.14 mm等量增加到0.21 mm,增量Δh=0.01 mm,以获取J-P系统最优扩径量。
图7是不同扩径量装配完成后恢复至室温时J-P系统的von Mises应力云图。由图7可见,J-P系统应力分布沿中面(图2选取点所在横截面)对称分布。当h=0.14 mm时,NiTiNb SMA管接头von Mises应力分布均匀,没有出现明显的应力集中区;h=0.15 mm时,开始出现明显的应力集中,当h由0.15 mm等量增加到0.21 mm时,其应力集中区逐渐沿径向由内表面向外移动。在管接头与被连接管接触以外区域,被连接管内的应力分布沿轴向呈现较大的应力梯度,且距中面大于7.5 mm (被连接管的远离管接头一端)时,被连接管内应力为零。
图7

图7 不同扩径量(h)下的von Mises应力云图
Fig.7 von Mises stress distributions with diameter expansions h=0.14 mm (a), h=0.15 mm (b), h=0.16 mm (c), h=0.17 mm (d), h=0.18 mm (e), h=0.19 mm (f), h=0.20 mm (g) and h=0.21 mm (h)
Color online
NiTiNb SMA管接头内表面接触压力分布如图8所示。可见,其内表面接触压力分布不均匀且沿中心面对称分布。图9是不同扩径量下得到的拉拔力关系曲线。可见,随着扩径量的增加,拉拔力逐渐减小。对比图8和9可见,h在0.14~0.16 mm范围内时,NiTiNb SMA管接头内表面应力分布较为均匀,对应的拉拔力波动较小;h在0.17~0.21 mm范围内时,NiTiNb SMA管接头内表面应力分布出现明显的不均匀分布,随着h增加,NiTiNb SMA管接头内表面两端部的接触应力逐渐减小,管接头端部两侧的接触压力减小的范围逐渐增加,拉拔力随之降低。可见,NiTiNb SMA管接头内表面两端部的接触压力显著影响NiTiNb J-P系统拉拔力。
图8

图8 不同h下NiTiNb SMA管接头内表面接触压力云图
Fig.8 Contact pressure distributions of inner surface of NiTiNb SMA joint with h=0.14 mm (a), h=0.15 mm (b), h=0.16 mm (c), h=0.17 mm (d), h=0.18 mm (e), h=0.19 mm (f), h=0.20 mm (g) and h=0.21mm (h)
Color online
图9

图9 拉拔力与扩径量变化关系图
Fig.9 Relationship between pull-out force and h
4.2 壁厚尺寸对J-P系统装配性能的影响
为找出在不同外径尺寸下,可以提供较大抱紧力的J-P系统尺寸匹配方案,将NiTiNb SMA管接头长度(LJ)设定为11.00 mm,内径(rJ)设定为3.00 mm,管接头的外径(WJ)设定为3种不同壁厚尺寸,从5.60 mm等量逐次递减到4.40 mm,详见表2。被连接管的长度(LP)设定为7.50 mm,内径(rP)设定为2.00 mm,被连接管的外径(WP)也设定为3种不同壁厚尺寸,从3.10 mm等量逐次增加到3.22 mm,详见表3。根据不同尺寸方案配比(表4),被连接管的壁厚从0.55 mm等量逐次增加到0.61 mm;NiTiNb SMA管接头的壁厚从1.30 mm等量逐次递减到0.70 mm,共9组不同匹配方案。
表2 NiTiNb SMA 管接头尺寸参数设定表 (mm)
Table 2 NiTiNb SMA joint size parameter setting table (mm)
|
Scheme
|
LJ
|
rJ
|
WJ
|
|
J1
|
11.00
|
3.00
|
5.60
|
|
J2
|
11.00
|
3.00
|
5.00
|
|
J3
|
11.00
|
3.00
|
4.40
|
新窗口打开| 下载CSV
表3 被连接管尺寸参数设定表 (mm)
Table 3 Connected pipe size parameter setting table (mm)
|
Scheme
|
LP
|
rP
|
WP
|
|
P1
|
7.50
|
2.00
|
3.10
|
|
P2
|
7.50
|
2.00
|
3.16
|
|
P3
|
7.50
|
2.00
|
3.22
|
新窗口打开| 下载CSV
表4 NiTiNb J-P系统尺寸参数设定方案表 (mm)
Table 4 NiTiNb J-P system size parameter setting scheme table (mm)
|
Scheme
|
NiTiNb SMA joint
|
Connected pipe
|
|
rJ
|
WJ
|
HJ
|
rP
|
WP
|
HP
|
|
1
|
3.00
|
5.60
|
1.30
|
2.00
|
3.10
|
0.55
|
|
2
|
|
|
|
|
3.16
|
0.58
|
|
3
|
|
|
|
|
3.22
|
0.61
|
|
4
|
3.00
|
5.00
|
1.00
|
2.00
|
3.10
|
0.55
|
|
5
|
|
|
|
|
3.16
|
0.58
|
|
6
|
|
|
|
|
3.22
|
0.61
|
|
7
|
3.00
|
4.40
|
0.70
|
2.00
|
3.10
|
0.55
|
|
8
|
|
|
|
|
3.16
|
0.58
|
|
9
|
|
|
|
|
3.22
|
0.61
|
Note: HJ—thickness of SMA joint, HP—thickness of connected pipe
新窗口打开| 下载CSV
图10是方案1~9计算得到的NiTiNb SMA 管接头接触压力分布云图。图11为不同方案下接触面积及拉拔力的对应关系。对比图10和11可见,当NiTiNb SMA 管接头外半径WJ1/2=2.80 mm时(方案1~3),随着被连接管壁厚的增加,接触压力增加(图10a),接触面积增加(图11a),拉拔力随被连接管外半径的增加而增加(图11b);当NiTiNb SMA管接头外半径WJ2/2=2.50 mm时(方案4~6),接触压力变化不明显(图10b),拉拔力随着接触面积的增加而增加(图11b);NiTiNb SMA 管接头外半径WJ3/2=2.20 mm时(方案7~9),随被连接管外半径的增加,管接头两端部的接触压力减小(图10c),拉拔力随着接触压力的减小而减小(图11b)。
图10
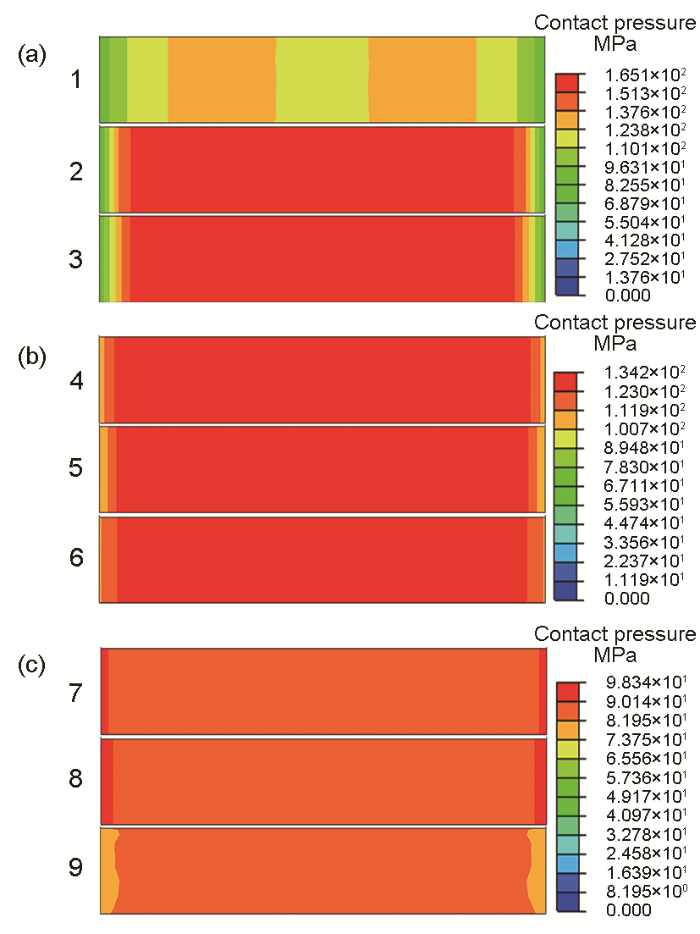
图10 方案1~9的NiTiNb SMA管接头内表面接触压力云图
Fig.10 Contact pressure distributions of NiTiNb SMA joint of schemes 1~3 (a), 4~6 (b) and 7~9 (c)
Color online
图11
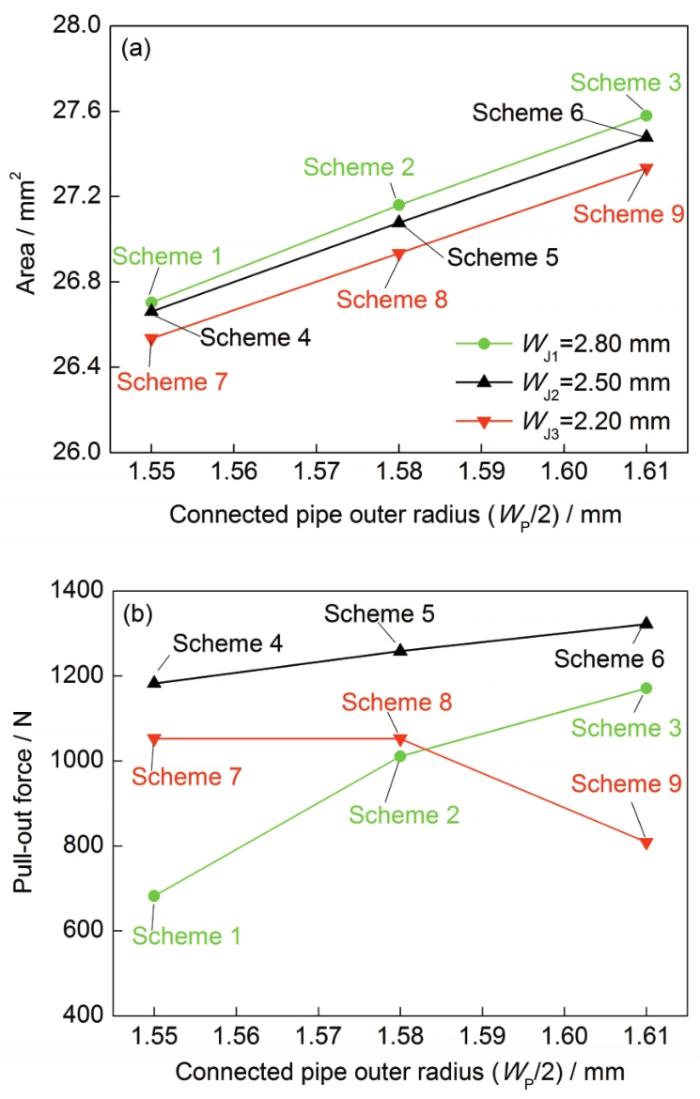
图11 接触面积和拉拔力随被连接管外半径变化关系曲线
Fig.11 Relationships between contact area (a), pull-out force (b) and outer radius of connected pipe
可见,在上述9种方案中,接触压力和拉拔力并不是随着NiTiNb SMA管接头壁厚的增大而线性增大,而是存在一个最大值点(NiTiNb SMA管接头外半径WJ2/2=2.50 mm),当NiTiNb SMA管接头外半径小于2.50 mm时,拉拔力随着被连接管外半径的增大而增加;当NiTiNb SMA管接头外半径超过2.50 mm时,拉拔力随着被连接管外半径的增大而减小。所以,在一定的尺寸范围内,温度为23 ℃时,当NiTiNb SMA管接头外半径WJ2/2=2.50 mm和被连接管外半径WP3/2=1.61 mm (方案6)时,可以提供较大的接触压力和拉拔力。
4.3 温度对J-P系统服役性能的影响
在上述9种外径尺寸方案基础之上,进一步计算了在一定服役温度范围内,拉拔力随温度变化的规律。分别计算在3、23和43 ℃环境温度J-P系统拉拔力,得出拉拔力随温度变化的曲线,如图12所示。在3~43 ℃服役温度范围内,拉拔力随着温度的升高呈现微弱的降低趋势,但变化较小(方案1、3~8),部分方案(方案2和9)出现拉拔力波动情况,总体来讲,在服役温度范围内,拉拔力受温度的影响较小,即在服役温度范围内,温度变化对J-P系统拉拔力的影响可以忽略不计。
图12

图12 拉拔力随温度变化曲线
Fig.12 Relationships between pull-out force and temperature
4.4 临界相变应变对J-P系统装配性能的影响
相同的扩径变形量下不同临界相变应变会导致塑性变形量不同。本部分讨论临界相变应变对J-P系统装配性能的影响。
不同临界相变应变下的拉伸应力-应变曲线如图13所示。可见,弹性阶段,应力-应变关系与临界相变应变无关;在屈服阶段和形变恢复阶段,随着临界相变应变的增加,塑性屈服点向右移动,应力峰值逐渐降低,卸载后残余应变逐渐增加。
图13
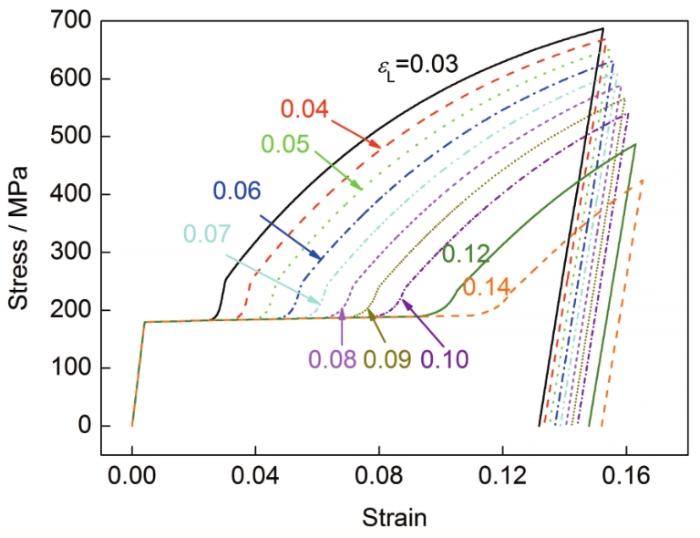
图13 不同临界相变应变(εL)下的应力-应变曲线
Fig.13 Stress-strain curves under different critical phase transformation strains (εL)
图14a1~a10是方案6在23 ℃不同临界相变应变下J-P系统的von Mises应力云图,同时提取NiTiNb SMA管接头横截面上的von Mises应力分布,如图14b1~b10所示。由图14a1~a10可见,临界相变应变显著影响J-P系统接触后的应力状态:随着临界相变应变增加,被连接管的von Mises应力先增加后减小。J-P系统von Mises应力沿轴向均匀分布。值得注意的是,从接触后NiTiNb SMA管接头横截面的von Mises应力分布(图14b1~b10)可见,当临界相变应变为0.03时,最大应力层位于管接头外侧,随着临界相变应变增加,最大应力层的位置逐渐向内侧移动,当临界相变应变达到0.1时,最大应力层位于管接头最内层。临界相变应变继续增加,最大应力层消失,管接头内应力分布达到较均匀状态。说明相同的扩径量下,临界相变应变不同,管接头内的应力分布不同,从而将影响其接触压力和拉拔力。
图14
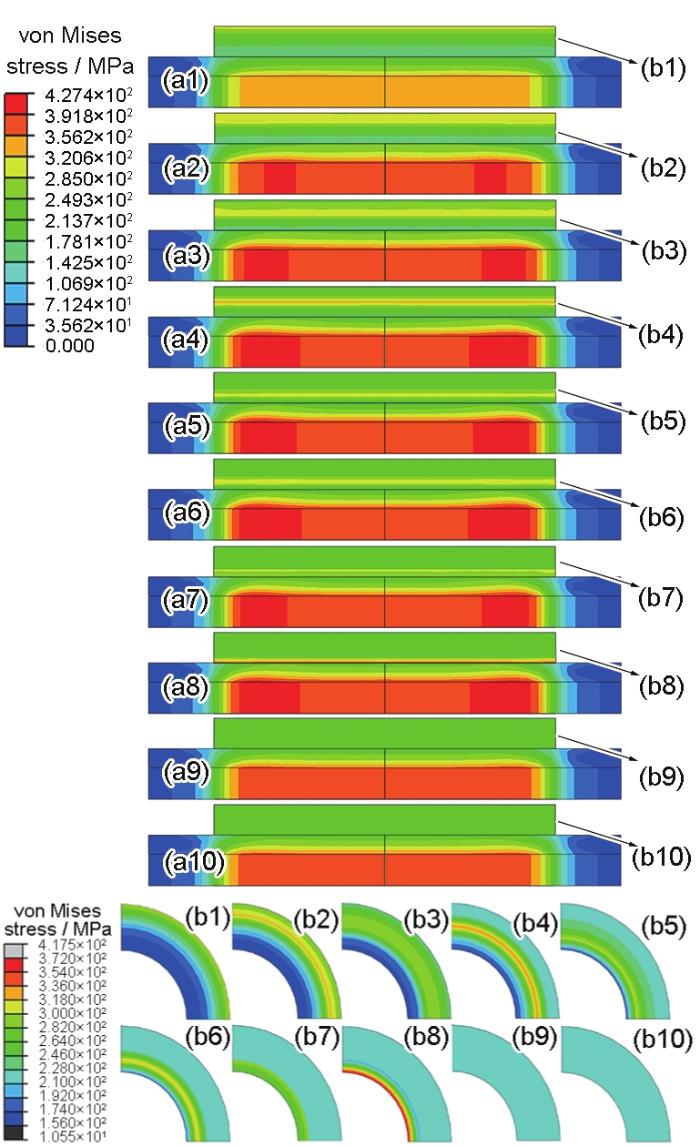
图14 不同临界相变应变下NiTiNb J-P 系统的von Mises应力云图和NiTiNb SMA管接头横截面von Mises应力云图
Fig.14 von Mises stress distributions of NiTiNb J-P system under εL=0.03 (a1), εL=0.04 (a2), εL=0.05 (a3), εL=0.06 (a4), εL=0.07 (a5), εL=0.08 (a6), εL=0.09 (a7), εL=0.10 (a8), εL=0.12 (a9), εL=0.14 (a10) and corresponding NiTiNb SMA joint (b1~b10)
Color online
图15是不同临界相变应变下的接触压力云图,图16是不同临界相变应变下对应的拉拔力-相变应变关系曲线。结合图15和16可见,当临界相变应变由0.03增加到0.04时,接触压力明显增加,拉拔力增大;当临界相变应变为0.04时,拉拔力达到最大值;临界相变应变由0.04增加到0.07时,拉接触压力和拉拔力逐渐减小;临界相变应变由0.07增加到0.10时,拉拔力逐渐增加;临界相变应变由0.10增加到0.14,拉拔力稳定。综上所述,当临界相变应变由0.03增加到0.07时,von Mises应力和接触压力不稳定,拉拔力波动较大;当临界相变应变由0.07增加到0.14时,von Mises应力和接触压力规律性较强,拉拔力稳定。整体来讲,不同临界相变应变对应的拉拔力都在1200 N以上。
图15

图15 不同临界相变应变下管接头内表面接触压力云图
Fig.15 Contact pressure distributions of pipe inner surface under εL=0.03 (a), εL=0.04 (b), εL=0.05 (c), εL=0.06 (d), εL=0.07 (e), εL=0.08 (f), εL=0.09 (g), εL=0.10 (h), εL=0.12 (i) and εL=0.14 (j)
Color online
图16

图16 临界相变应变与拉拔力关系曲线
Fig.16 Relationship between εL and pull-out force
考虑到实际服役情况,当临界相变应变小于0.05时von Mises应力最大值在管接头外边缘,且在管接头两端部有应力集中,复杂的外界条件(腐蚀、氧化、温差等)会显著影响J-P系统的连接效果,不利于整体性能的稳定;临界相变应变在0.06到0.14范围内,拉拔力随临界相变应变的增加而增加,规律性较强,且应力最大值集中在管接头中端;临界相变应变大于0.12后,von Mises应力沿管接头呈阶梯状均匀分布,拉拔力与临界相变应变关系曲线趋于稳定。
5 各变量对拉拔力的影响比重
不难看出,在NiTiNb SMA管接头两端接触压力较大时,对应的拉拔力也较大(见图8,9,15和16);在NiTiNb SMA管接头两端接触压力相差不大时,NiTiNb SMA管接头中间段的接触压力决定了拉拔力的大小。究其原因,是在相同模型尺寸条件下,拉拔力对NiTiNb SMA管接头集中应力的存在较为敏感,致使在NiTiNb SMA管接头两端应力较大时,所提供的拉拔力较大。因此,采取含内脊型管接头将会显著增加其抱紧力,增强连接性能[20,27,28]。
影响NiTiNb SMA J-P系统拉拔力的因素众多,本工作主要考虑扩径量、壁厚、服役温度及临界相变应变等4个因素对系统von Mises应力、接触压力以及拉拔力的影响。
(13)(14)
式中,pi (i=1, 2, 3, 4)分别表示扩径量、壁厚、服役温度和临界相变应变条件下的拉拔力变化范围;pmax为对应的拉拔力最大值;pmin为对应的拉拔力最小值;ni (i=1, 2, 3, 4)分别表示在不同研究因素中的影响比重。
将各个影响因素绘制成比例图,如图17所示。不难看出,临界相变应变是比重最大的影响因素,对拉拔力的影响比重占比达40.59%;扩径量的影响比重次之,达到了33.96%;壁厚的影响比重为23.60%;服役温度范围的影响比重极小,只占1.85%,是影响最弱的,表明在一般室外温度变化范围内(0~40 ℃),SMA J-P系统的连接性能几乎不受影响。
图17
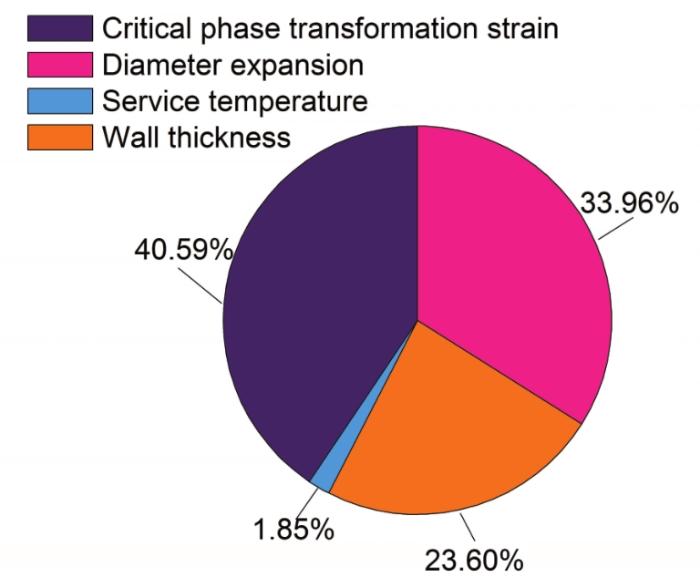
图17 不同因素对拉拔力的影响比重
Fig.17 Proportion of factors affecting pull-out force
Color online
6 结论
(1) 由于马氏体相变和塑性变形的综合作用,装配全过程von Mises应力、等效相变应变和等效塑性应变呈现明显的规律性变化特征:在加载阶段,随着预变形量的增加,相变应变和塑性变形增加;在随后的各加载步,塑性应变保持不变;卸载阶段,von Mises应力减小,相变应变保持不变;升温后相变应变显著减小,von Mises应力增加;在随后的加载步,von Mises应力和相变应变都保持不变。
(2) 在给定尺寸条件下,随着扩径量的增加,管接头内应力集中层沿径向由内表面向外移动,同时拉拔力呈减小趋势。
(3) 对本工作模拟的9种不同壁厚的NiTiNb SMA J-P系统中,当SMA管接头外半径为2.50 mm和被连接管外半径为1.61 mm (方案6)时,所提供的拉拔力最大。
(4) 在一般室外温度变化范围内(0~40 ℃),服役环境温度对NiTiNb SMA管接头连接系统的性能影响较小,工程应用中可以不予考虑。
(5) 在给定尺寸和温度条件下,临界相变应变的增加会使管接头内应力集中层由外侧向内侧移动,在NiTi基合金的临界相变应变范围内(大于0.07),增加临界相变应变可增强NiTiNb J-P系统的接触压力和拉拔力,提高NiTiNb J-P系统的整体稳定性。
























 沪公网安备31011202020290号
沪公网安备31011202020290号
