分享:钛合金薄壁件选区激光熔化应力演变的数值模拟
建立了选区激光熔化(SLM)热-结构耦合瞬时动态有限元模型,探究了激光扫描速率和铺粉层厚度对SLM成形钛合金薄壁件应力演变的影响。结果表明,在热循环作用下,SLM成形钛合金薄壁件的应力演变呈周期性变化。在热应力循环去应力退火作用下,热应力极大值在加热阶段先增加后减小,最后在冷却阶段趋于稳定并接近残余应力。SLM成形薄壁件最终残余应力小于加热过程中的瞬时应力峰值。随沉积高度的增加,热循环作用减弱,应力极大值下降幅度逐渐减小。经过多次热循环去应力退火作用后,SLM成形薄壁件过程中的热应力极大值下降幅度可达30%以上。
关键词:
钛合金复杂薄壁件因其结构轻、功能多样化而被广泛应用于航空航天等领域[1,2]。选区激光熔化(selective laser melting,SLM)技术基于分层制造、层层叠加原理,具有光斑直径小、成形精度高、成形零件形状复杂等特点,成为近年来发展迅速的金属增材制造(additive manufacturing,AM)技术之一[3,4]。相较于传统工艺,采用SLM技术成形复杂薄壁结构件可在节省80%制造时间的同时降低20%~50%的成本,是快速制造高精度[5]、高性能[6,7]金属薄壁件的理想手段。然而,由于SLM成形时具有激光热源移动速率快和局部加热不均匀等特点,致使成形件冷却速率高、温度梯度大,冷却后将产生较大的残余应力并变形,最终可能导致成形失败[8]。采用基于实验验证的数值模拟分析方法,可替代大量的重复实验,是探究SLM成形过程中应力演变规律的有效方法。
自Mercelis和Kruth[9]提出采用温度梯度机制(temperature gradient mechanism,TGM)阐释SLM成形过程残余应力形成机制以来,国内外学者相继开展了系列研究。在国内,Liu等[10]采用X射线衍射法研究了沉积高度、支撑对SLM成形不锈钢试样的影响,指出层间后续热循环[11]对试样沿沉积高度的热应力分布影响显著;Gu和He[12]采用有限元法研究了SLM成形TiNi形状记忆合金的热应力演变规律及其与试样开裂行为的内在联系;文舒等[13]建立并验证了SLM成形GH536合金的热力耦合有限元模型,发现SLM成形试样表面存在较大拉应力,随着沉积高度降低转变为压应力;陈德宁等[14]对不同扫描模式下SLM成形钛合金应力场进行了分析,发现分区扫描比光栅扫描获得的温度场分布更均匀,有利于减少应力集中;徐仁俊[15]对Ti-6Al-4V单层成形过程的应力场分布进行数值模拟,并分析了扫描道长度和不同扫描模式对应力场的影响;此外,西北工业大学[16]、中北大学[17]和华中科技大学[18,19]等单位也开展了SLM成形不锈钢、高温合金和钛合金的应力研究。在国外,Parry等[20]采用有限元模拟研究了单向和交替扫描下成形过程中的热应力分布,结果表明SLM成形时的应力分布呈各向异性;Yadroitsev和Yadroitsava[21]采用数值计算和中子衍射实验相结合的方式研究了Ti-6Al-4V合金和不锈钢SLM成形的残余应力分布,发现沿激光扫描方向的温度梯度较大,使得该方向的热应力较大;Ali等[22]研究了扫描模式以及重熔方式对Ti-6Al-4V合金成形残余应力的影响;Denlinger等[23]和Li等[24]研究了高温合金多层多道成形过程中的应力分布,研究表明,先沉积层表现为较大拉应力,随后逐渐向压应力转变,沉积过程中沿沉积高度方向的应力逐渐增加。
综上,目前关于SLM应力的报道多集中在SLM成形冷却后的残余应力。SLM高精度成形的特点使其有限元模型具有时间、空间多尺度的特性,这增加了模型的建模和资源优化分配的难度,导致SLM瞬时动态应力的研究报道不多。实际上,SLM成形过程中热循环诱导产生的热应力将影响整个成形过程,对成形件应力和变形的演变过程非常重要。因此,本工作采用热-结构耦合瞬时动态SLM有限元模型,并通过实验对该模型的计算结果进行验证,进而探究激光扫描速率和铺粉层厚度对SLM成形钛合金薄壁结构件应力演变的影响,以期为SLM成形过程的应力、变形和开裂控制提供理论支持。
SLM成形原理是激光对预置金属粉末床进行选择性加热熔化,进而逐点-逐线-逐层沉积成实体构件。为了更真实地反映SLM增材成形过程,本工作建立的SLM应力演变有限元模型不仅考虑了激光作用前后粉末态到实体态热物性参数等特性的转变[25],而且在热分析时记录下激光加热过程中每个时刻对应转变的实体单元,并建立“单元编号-单元坐标-热历史温度-激活时刻”数据库,然后在结构分析中根据该数据库将每个时刻对应的实体单元增量逐步激活,以实现SLM逐点沉积过程中瞬时动态应力演变的模拟计算。本工作采用MATLAB以及ANSYS参数化设计语言(ANSYS parameter design language,APDL)建立了SLM成形钛合金热-结构耦合模型,将温度场求解结果作为热载荷施加至应力场进行求解。
在SLM成形温度数值模拟中,由于SLM激光与粉末相互作用经历了热传导、热对流、热辐射、相变等一系列复杂过程,具有明显的非线性瞬态热传导特征,其热传递控制方程满足[26]:
式中,kx、ky和kz分别为x、y和z方向热导率;ωx、ωy和ωz分别为x、y和z方向热导率增强系数;t为加工时间;T为粉床温度;
式中,T0为初始温度,根据实际工况设置为25 ℃。边界条件主要包括热对流和热辐射。SLM成形过程中边界处因对流散失的热量(qc)和辐射散失的热量(qr)可表示为:
式中,ε为物体在环境中的发射率;Tamb为环境温度;σSB为Stefan-Boltzmann常数,取5.67×10-8 W/(m2·℃);hconv是自然对流系数,取25 W/(m2·℃)。本工作将对流和辐射边界条件统一用复合换热系数(hcomb)表示以提高求解效率[27]:
式中,P为激光功率;A为Ti-6Al-4V金属粉末对该波长激光的吸收率,本工作中取0.42[30];r0为光斑半径;v为激光扫描速率。
SLM成形应力数值模拟中,材料应力应变行为符合热-弹-塑性原理。在塑性变形过程中,考虑材料应力应变行为遵循流动准则和等向强化准则。应力和应变之间的内在关系为[31]:
式中,{σ}是应力向量;[D]是弹性矩阵;{εe}为弹性应变向量,可表示为:
式中,{ε}、{εp}和{εth}分别是总应变向量、塑性应变向量和热应变向量。其中热应变(εth)可用温度(T)和材料热膨胀系数(α)表示:
式中,Tref为参考温度。在SLM应力演变的分析中,采用Mises屈服准则表示等效应力(
式中,σ1、σ2和σ3为3个相互垂直方向上的主应力。同理,等效应变(
式中,ε1、ε2和ε3为3个方向上的主应变;μ为Poisson比。求解前,将基板底部温度设定为室温,并将基板底部节点的x、y和z方向位移约束设置为零。为了提升模型精度和计算效率,网格划分时将有限元模型中的粉床分为激光直接作用区域与远离激光直接作用区域。激光直接作用区域温度梯度大,采用较细的六面体划分网格(最小网格体积为4×103 μm3),远离激光作用区域采用渐变粗化式的网格进行划分。基板区域则采用凸台过渡的方式划分网格。本工作有限元模型节点数超过1×106个,相关模拟计算在WNLO-HPC高性能计算平台进行。
SLM加工过程中,金属粉末在激光作用下经历了由粉末态至液态以及固态的转变,不同温度和状态下材料的性能参数差异较大。因此,为了提高求解精度需采用随温度和物态变化的热物性参数。
图1 Ti-6Al-4V合金热导率和体积焓随温度的变化规律
Fig.1 Temperature dependency of thermal conductivity (a) and volumetric enthalpy (b) of Ti-6Al-4V alloy(Tliquid—liquidus temperature, Tα→β—temperature of transition from α phase to β phase of Ti-6Al-4V alloy)
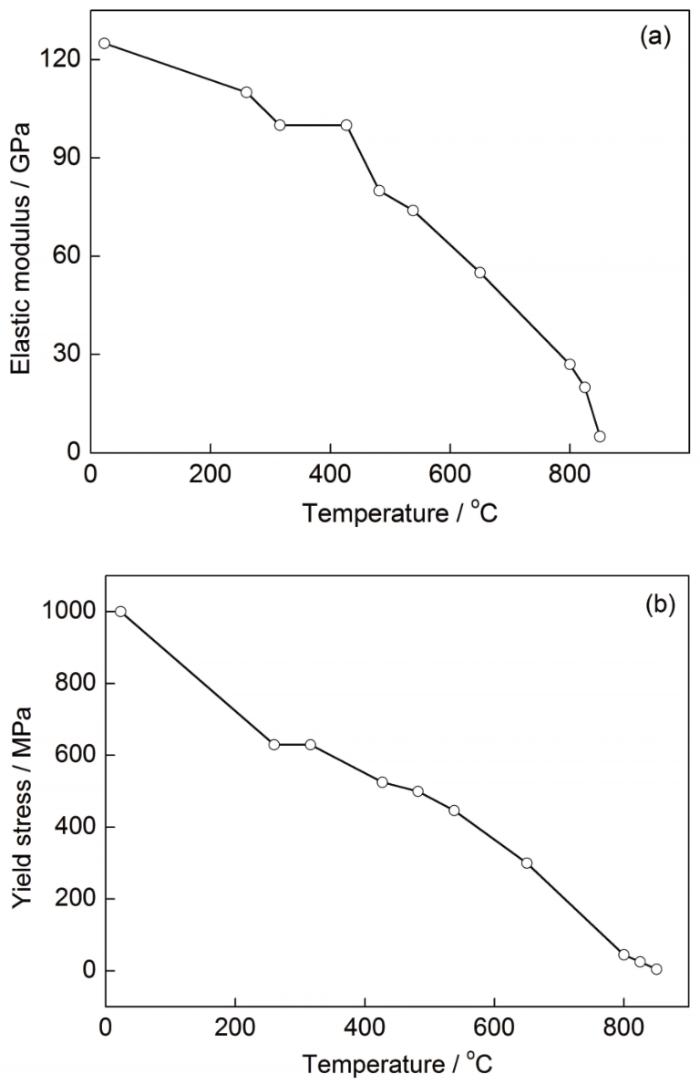
图2 Ti-6Al-4V合金弹性模量和屈服强度随温度的变化规律
Fig.2 Temperature dependency of elastic modulus (a) and yield strength (b) of Ti-6Al-4V alloy
图3为数值模拟计算不同激光扫描速率下SLM成形钛合金薄壁件的温度分布云图和熔池形貌演变规律。在图中根据Ti-6Al-4V的Tliquid=1650 ℃标识出熔池轮廓线,并测量熔池尺寸。箭头则表示熔池尾部固/液界面处的最大热流方向。
图3 选区激光熔化(SLM)成形Ti-6Al-4V合金薄壁件在不同激光扫描速率下的温度分布和熔池演变
Fig.3 Temperature distributions and molten pool evolutions in the longitudinal mid-section during selective laser melting(SLM) of Ti-6Al-4V thin-walled parts under different laser scan rates of 1000 mm/s (a), 700 mm/s (b) and 500 mm/s (c) (The colored arrow vectors represent the maximum heat flow directions at the tail of the molten pool boundary)
Color online
图4 不同激光扫描速率下熔池尺寸的数值模拟与实验结果对比
Fig.4 Comparisons of simulation and experimental results of the molten pool width and depth at the cross-section under different laser scan rates (Insets show the OM images of molten pools under scanning velocities of 500, 700 and 1000 mm/s, respectively)
图5 SLM成形Ti-6Al-4V合金薄壁件晶粒生长方向的数值模拟与实验结果对比
Fig.5 Comparisons of simulation and experimental results of grain growth orientation during SLM of Ti-6Al-4V thin-walled parts (The tilt angles between the maximum heat ?ow directions and the building direction can be calculated from the temperature gradients at the tail of the molten pool boundary (θsim), and also measured experimentally by analyzing optical micrographs (θexp))
Color online
式中,i和j分别为x方向和z方向的方向矢量;Gh和Gv分别为x方向(激光扫描方向)和z方向(沉积方向)的温度梯度。如图5所示,钛合金薄壁件SLM成形过程中,柱状晶沿着沉积方向生长,并朝着激光扫描方向偏离,其偏离程度随着层数增加而逐渐降低并趋缓,并且随着激光扫描速率降低而增加。激光扫描速率为1000、700和500 mm/s时对应的偏离角度分别为θsim_1=10.99°、θsim_2=12.21°和θsim_3=13.45°。通过将温度场熔池固/液界面热流方向与试样金相的柱状晶生长方向(θexp_1=11.43°)进行比较,表明其在误差范围内与实验结果符合较好,从而验证了SLM温度场模型的有效性。
本工作采用Stress Technologies的X-350A型X射线衍射仪(XRD)测量SLM成形薄壁件的残余应力。实验测试点位于薄壁侧面从基板到试样顶部沿z方向等距离(5 mm)分布,考虑实验测量结果为衍射光斑直径(约3 mm)范围内的平均值,因此数值模拟结果也取对应位置范围内节点计算结果的平均值。实验试样与模拟试样的尺寸均为50 mm×5 mm×20 mm,在30 kV、6.7 mA条件下测量试样中Ti-α{110}的晶格变形。
图6为激光功率300 W、扫描速率1000 mm/s、铺粉厚度40 μm时,SLM成形钛合金薄壁件残余应力实验测量与模拟预测结果的对比。对于左侧节点(图6a),沉积高度为7.5 mm时,模拟结果与实验测量值最为接近,两者的差别小于17 MPa,薄壁试样顶部节点的差别最大,最大差值为96 MPa;对于右侧节点(图6b),模拟预测结果与实验测量的最大差值仅为32 MPa。此外,模拟预测结果的整体趋势比实验测量结果更大,这是因为试样成形完成至应力测量之间存在一定的时间滞后,在自然时效退火作用下,其残余应力将得到一定程度的释放。综上,模拟与实验的误差在可接受范围内,所建立模型能够较准确地预测SLM成形过程中的应力演变规律。
图6 SLM成形薄壁件残余应力的数值模拟与实验结果对比
Fig.6 Comparisons of simulation and experimental results of residual stress in SLM of thin-wall parts
(a) left nodes (b) right nodes
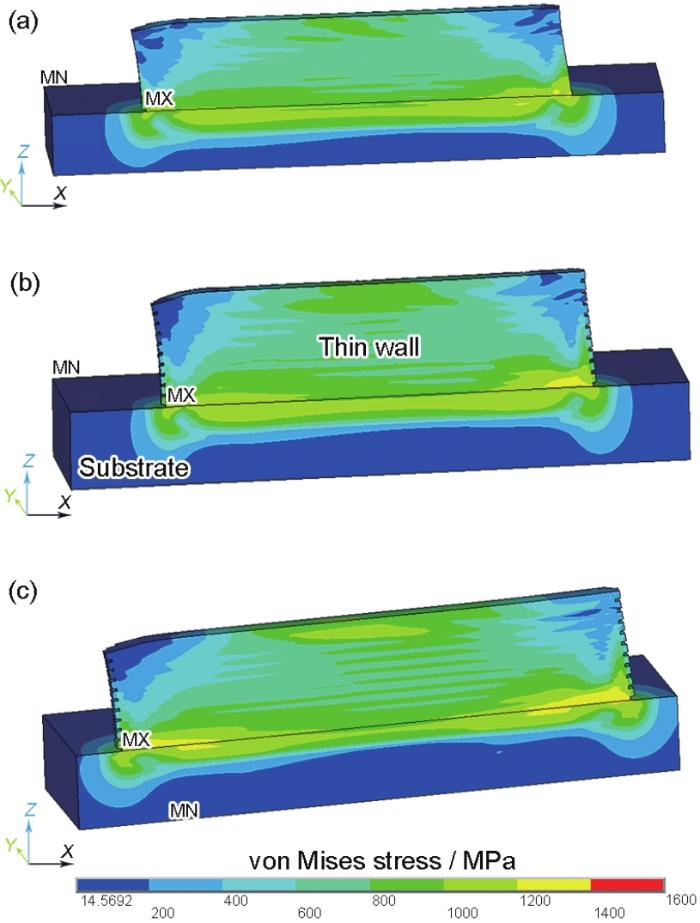
图7所示是激光功率为300 W、铺粉厚度为40 μm条件下,激光扫描速率分别为500、700和1000 mm/s时冷却至室温后成形薄壁件的等效应力分布云图。可见,不同扫描速率下成形薄壁件的应力分布趋势差别较小,但薄壁件与基板交界处高应力区域的分布范围随激光扫描速率增加而增大,说明激光扫描速率较高时开裂倾向更为明显。温度空间分布的不均匀性是产生应力的主要原因,工艺参数影响了SLM成形时的热影响区范围及温度梯度,进而改变了残余应力的分布。
图7 激光扫描速率对SLM成形钛合金薄壁件应力的影响
Fig.7 Effects of laser scan rate on the stress distribution in SLM of thin-wall parts (MN indicates the minimum residual stress, and MX indicates the maximum residual stress)
Color online
(a) 500 mm/s (b) 700 mm/s (c) 1000 mm/s
从图7可知,随着激光扫描速率的增加,薄壁件内部热应力逐渐增大。以薄壁件顶部中间位置节点为例,扫描速率为500 mm/s时对应的最大等效应力为787.43 MPa;随着扫描速率增加至700和1000 mm/s,最大等效应力分别增加至942.76和1002.48 MPa,热应力的增幅分别为19.73%和6.33%。这是因为增大激光扫描速率意味着缩短激光停留时间,从而使得已扫描区域的冷却速率增大,薄壁件局部快速冷却产生不均匀的温度分布。当激光分别以扫描速率为500、700和1000 mm/s远离薄壁件顶部中间节点时,该节点处的温度梯度分别为2.86、3.63和5.05 ℃/μm,导致SLM在高速下产生的残余应力相对较大。
图8为不同铺粉厚度下第一层上表面中间节点D1示意图,以及D1的热应力循环和热循环的演变规律,黑色竖直虚线标识每一层加工的时间跨度,层间铺粉时间设置为20 s。图8b表明,在热循环作用下,SLM成形钛合金薄壁件的应力演变呈周期性变化。在热应力循环去应力退火作用下,热应力峰在SLM成形阶段先增加后减小,最后在SLM成形最终冷却后趋缓并接近残余应力。以层厚40 μm时为例,D1的热应力极大值从第2层时的1080.43 MPa增加到第3层时的1130.01 MPa,随后随沉积高度增加而逐渐下降(第4、6、8、10层对应的极大值分别为1050.39、953.26、924.49和894.43 MPa),最后SLM成形后热应力在910 MPa附近趋缓。
图8 SLM成形钛合金薄壁件第1层上表面节点D1示意图及不同铺粉层厚度条件下的热应力循环与热循环
Fig.8 Schematic of D1 node at the upper surface of 1st layer of the thin-wall parts (a), and effects of layer thickness on the thermal stress cycle (b) and thermal cycle (c) (σn_max and σn_min represent the maximum stress and the minimum stress in each thermal stress cycle during SLM, respectively; σresidual is the residual stress in the final cooling stage; Tn_max represents the maximum temperature during each thermal cycle; Tannealing is the annealing temperature of Ti-6Al-4V alloy)
图8c表明,在铺粉层厚度40和50 μm条件下,SLM成形钛合金薄壁件时D1节点都分别经历了3次1650 ℃以上的“固-液-固”相变热循环,而层厚60 μm时经历了2次1650 ℃以上的热循环。此外,铺粉层厚度为40 μm时经历了5次800 ℃以上温度的热循环,而层厚50和60 μm时则经历了4次800 ℃热循环。不同铺粉厚度条件下层间热循环作用的差异影响了SLM成形薄壁件内部的热应力循环。最终冷却至室温时刻的残余应力随铺粉层厚度减少而增加。SLM成形结束冷却至室温时,铺粉厚度为40、50和60 μm时对应的残余应力分别下降至910.12、787.26和796.58 MPa,与D1节点成形过程中的最大热应力(第3层)相比,最终冷却至室温时热应力下降的幅度分别为19.46%、30.81%和24.99%。
图9 热循环去应力退火作用下不同铺粉厚度时冷却阶段节点D1的热应力下降幅度和比例
Fig.9 Decreases in amount (a) and percentage decreases (b) of the thermal stress of D1 node in cooling stage as a function of subsequent thermal cycle under different layer thicknesses
当铺粉厚度为40 μm时,相比第3层冷却阶段节点D1的最大热应力,经历第4层热循环的去应力退火作用后D1的最大热应力减小了79.62 MPa,下降幅度为7.05%。这是因为当铺粉厚度为40 μm时,第4层激光关闭后冷却阶段节点D1的最大冷却速率可达5.99×105 ℃/s,此时刻D1处的温度梯度为15.44 ℃/μm,快速冷却下不均匀的温度分布导致较高的残余应力。当铺粉厚度增加至50和60 μm时,对应的温度梯度分别减小至4.55和3.27 ℃/μm。较低的温度梯度使得冷却后的残余应力相对较小,因此该层冷却阶段的热应力极大值σ4_max较之前降幅更大,分别为19.97%和15.49%。激光作用于后续加工层时对该节点仍存在加热作用,不均匀的加热将使节点热应力先短暂上升,随着温度升高材料屈服强度逐渐下降,当试样内应力超过材料屈服强度时,材料将由弹性阶段进入塑性阶段,产生塑性变形使得内部应力得到释放。
SLM成形薄壁件时热循环的温度峰值越高,停留时间越长,去应力退火效果越明显。由图8可知,当SLM成形第4层时,D1在不同铺粉层厚度条件下(40、50和60 μm)的热循环峰值温度都在800 ℃以上,对应其在该层的热应力极小值σ4_min都小于20 MPa (分别为8.94、10.72和19.34 MPa),较之应力极大值的降幅超过95%。当SLM沉积第5层时,铺粉层厚度为40、50和60 μm时D1节点的热循环峰值温度分别是916.05、724.86和597.26 ℃,使其在第5次热应力循环时的热应力极小值差别较大,σ5_min由6.15 MPa提高至29.77 MPa和181.07 MPa。由图2b可知,各峰值温度下对应的材料屈服强度分别为22.4、182.36和353.21 MPa。屈服强度越低,试样塑性变形越剧烈,热应力下降越明显。因此,根据热应力循环中极小值对应的热循环温度可以推断,SLM成形钛合金薄壁件去应力退火的最佳温度范围在700~900℃。该温度范围小于图1中Ti-6Al-4V合金α相到β相的转变温度,可尽量在消除应力的同时避免组织变化或晶粒粗化导致的试样性能下降。
图10统计了节点D1在不同热循环作用下,加热阶段热应力下降幅度以及下降比例的变化规律。可知,较大铺粉厚度对应的热应力下降的幅度较小。此外,当铺粉厚度一定时,随着沉积层数增加,后续热循环强度和次数减少,加热阶段应力下降的百分比逐渐减小,由超过90%下降至40%左右。
图10 热循环去应力退火作用下不同铺粉厚度时加热阶段节点D1热应力下降幅度及比例
Fig.10 Decreases in amount (a) and percentage decreases (b) of the thermal stress of D1 node in heating stage as a function of subsequent thermal cycle under different layer thicknesses
上述结果表明:SLM成形钛合金薄壁过程中热应力循环的退火效果与热循环的峰值和次数有密切联系,与常规的钛合金热处理方法(如完全退火态[41]:800 ℃保温2 h、空冷)相比,SLM原位去应力退火的温度非恒定(102~103 ℃),并且作用时间极短(10-3~10-1 s)。因此,在研究和掌握SLM成形过程中热应力循环特点的基础上,应当优化激光功率密度和铺粉层厚度等工艺条件,通过调控SLM成形时的应力水平,达到抑制SLM成形过程中变形和开裂的目的。
(1) 建立了热-结构耦合瞬时动态SLM有限元模型,相关模拟结果分别在介观尺度的熔池尺寸、微观尺度的晶粒生长方向和宏观尺度的残余应力与实验结果符合较好,从多个尺度对SLM成形Ti-6Al-4V薄壁件有限元模型的温度场和应力场进行了验证。
(2) 在热循环作用下,SLM成形钛合金薄壁件的应力演变呈周期性变化。在热应力循环去应力退火作用下,热应力峰在SLM成形阶段先增加后减小,最后在SLM成形最终冷却后趋缓并接近残余应力。表明SLM成形钛合金薄壁件的瞬时热应力较高,其峰值甚至大于最终冷却后的残余应力,易在加热过程中诱发变形甚至开裂。
(3) 激光扫描速率对SLM成形薄壁件残余应力分布趋势的影响较小,但高应力区域的分布范围随着扫描速率的增加而扩大,并且薄壁件内部热应力逐渐增大,这是由于增加扫描速率缩短了激光停留时间,使得激光已成形区域的冷却速率增大进而产生了不均匀的温度分布。此外,随着铺粉层厚度增加,温度梯度减小,冷却后的残余应力也随之减小,因此热循环去应力退火后冷却阶段应力的降幅更大。
(4) 随着沉积高度的增加,热循环作用逐渐减弱,热应力极大值的下降幅度随之减小。经过多次热循环去应力退火作用后,SLM成形结束冷却至室温时热应力下降的幅度可达30%以上。根据SLM成形钛合金薄壁件热应力循环中极小值的演变规律,推断其去应力退火的最佳温度范围在700~900 ℃。
1 有限元模型的建立
1.1 SLM温度场有限元模型
1.2 SLM应力场有限元模型
2 材料热物性参数
图1

图2
3 分析讨论
3.1 SLM有限元模型的实验验证
图3
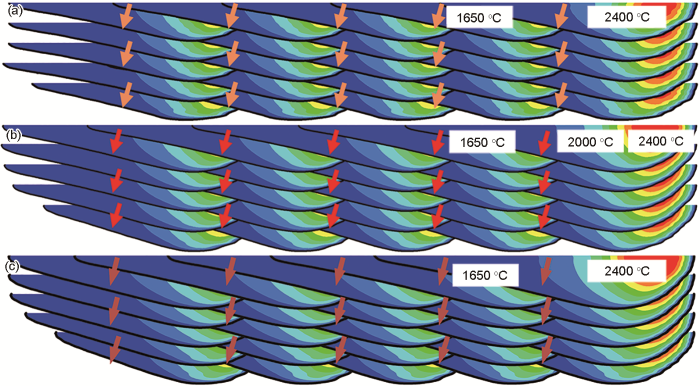
图4

图5

图6

3.2 SLM成形薄壁件的应力分布规律
图7
3.3 SLM成形薄壁件的应力演变规律
图8

3.3.1 SLM成形薄壁件热应力循环极大值的演变规律
图9

3.3.2 SLM成形薄壁件热应力循环极小值的演变规律
图10

4 结论
来源--金属学报







 沪公网安备31011202020290号
沪公网安备31011202020290号
