分享:Q&P钢热处理过程有限元法数值模拟模型研究
北京科技大学机械工程学院 北京 100083
以国内典型淬火-分配(Q&P)高强钢——QP980钢为例,进行热处理全过程物理模拟研究,提出一种耦合温度及时间影响的类蠕变应变方程用以描述材料在Q&P热处理分配过程的体积变化,建立考虑淬火温度影响的Q&P热处理两次淬火过程相变动力学方程、相变应变及相变塑性方程,获得了Q&P钢各相的热膨胀系数。根据温度场、组织场、应力场三场耦合原理,基于物理模拟得到的弹塑性增量本构模型,对商业有限元软件ABAQUS用户子程序进行二次开发,建立了针对Q&P热处理全过程的三场耦合数值仿真模型;通过Gleeble热-力模拟试验机上的Q&P热处理实验对模型进行了实验验证,实验结果与数值模拟结果吻合良好。
关键词:
先进高强钢(advanced high strength steel,AHSS)因其在力学性能、工艺要求、制造成本上的综合优势使其能够满足汽车及相关产业关于经济性、安全性以及轻量化的综合需求,成为了广受关注的原材料。科研人员基于对残余奥氏体相变诱导塑性(TRIP)效应机理[1,2,3]以及碳扩散行为[4,5]的研究,提出了区别于传统淬火-回火的以改进材料强度和韧性为目标的淬火-分配(quenching and partitioning,Q&P)热处理工艺,相较于第一、二代高强度钢,Q&P热处理工艺所选用的材料价格更低廉,在实现高强塑积的前提下降低了大规模工业生产的成本,具有很高的应用价值。但Q&P热处理过程存在复杂的热、力、相变耦合作用,板形问题一直是其工业生产中的突出问题。板形缺陷不仅会降低高强钢板带产品质量,影响下游产业的使用,还会对生产线的后续通板性、运行稳定性造成不利影响。研究板形缺陷在Q&P热处理过程中的演变机理和规律,能够为工业应用中的板形调控技术改进提供指导。
利用数值模拟方法对热处理过程温度场、组织场及应力应变场的演变历程及其耦合关系进行研究是一种共识,对研究材料在热处理中的宏观变形行为具有十分重要的意义。科研人员开发了应用于水淬[6,7,8]、渗碳淬火[9,10]、感应淬火[11]的数值模拟软件HEARTS (heat treatment simulation system)[12,13]和COSMAP (computer simulation of material process)[14]。近年来对相变塑性的机理和应用[15,16,17,18,19,20]进行了系统研究,提出了宏观有限元、细观相场和纳观分子动力学方法分析淬火过程耦合关系的研究思路[21]。Denis等[22,23]对淬火过程中应力与相变的耦合关系进行了梳理和总结,指出相变塑性对于材料内应力的演变存在重要影响。据此在对淬火过程的残余应力计算中全面考虑了相变塑性和应力对马氏体相变动力学的影响,并通过实验对计算结果进行验证。对于热处理过程而言,材料往往存在多种组织,不同组织的物性参数、组织之间相互转化的动力学关系及不同应力状态下的相变模型均存在很大差异。因此,建立实际材料精确的相变动力学模型[24]、相变塑性模型[25,26,27]、力学模型[28,29]、热传导模型,获得其精确的热物性参数,对于数值模拟结果的准确性有着决定性影响。
数值模拟模型也被应用于进行各类热处理过程的建模计算。Carlone等[30]对淬火过程的瞬态温度场进行了有限元分析,对奥氏体形成和分解进行了建模。Smoljan[31]对钢柱、锥、球的淬火过程的温度场和应力应变场进行有限元模拟,预测了任一时刻淬火样品的力学性能及残余应力与应变的分布。Bok等[32]通过ABAQUS用户子程序UMAT、VUMAT和HETVAL编程,对相变动力学和相变相关应力更新进行了有限元模拟,指出了相变应变对于计算结果的重要性。国内Song等[33]建立了有限元模型,模拟了齿轮齿圈渗碳淬火过程热处理中的微观结构和应力分布并进行了实验验证;Chen等[34]建立了一种基于热力学和内变量的非经典本构方程,并对淬火过程的组织、温度和应力场进行了计算;韩庆礼等[35]对钛合金焊接轴承钢的淬火过程进行了数值模拟研究,分析了多层材料温度场和应力场的变化,提出了减少微裂纹的淬火温度。
但是,目前对热处理的数值模拟研究范围主要集中在淬火和回火领域,而国内投入工业生产不久的Q&P热处理工艺与淬火和回火过程均存在较大差异,首先表现在Q&P热处理的第一次淬火过程,由于淬火结束温度较高使得材料马氏体相变不完全,接下来的升温并保温的分配过程,由于升温速率及保温时间均与回火过程存在量级上的差异,使马氏体中富集的C不是作为碳化物析出,而是扩散进入贫C的残余奥氏体,导致第二次淬火过程的组织场变化与一般淬火过程存在本质差别。目前针对这种新型热处理过程的三场耦合模拟研究鲜见报道。因此,对Q&P热处理过程进行数值模拟研究是对先前热处理过程仿真研究的有益补充。
本实验所用商业QP980钢,成分上为低碳Si-Mn钢的一种。钢的化学成分(质量分数,%)主要为:C 0.19,Mn 2.37,Si 1.73,Cr 0.011,S 0.0018,Fe余量,其中C、S元素检测遵照GB/T 20123-2006标准执行,Mn元素遵照NASIC/CH008:2013标准执行,Si元素遵照NASIC/CH009:2013标准执行,其余元素遵照NASIC/CH011:2013标准执行。设计QP980钢不同冷却速率的连续冷却实验方案如图1a所示,通过Gleeble热-力模拟实验测得钢的连续冷却转变(continuous cooling transformation,CCT)曲线如图1b所示。
图1 淬火-分配(Q&P) QP980高强钢的连续冷却实验方案及CCT曲线
Fig.1 Experimental scheme (a) and continuous cooling transformation (CCT) curves (b) of continuous cooling of quenching and partitioning (Q&P) QP980 steel (A—austenite, B—bainite, F—ferrite, M—martensite)
对不同冷速冷却后的常温组织按标准程序在自动磨样机上磨制抛光,使用4%硝酸酒精溶液进行腐蚀,采用EVO-18扫描电子显微镜(SEM,分辨率2.0 nm)观察其常温组织,工作电压20 kV,结果如图2所示。分析可知,在冷却速率大于30 ℃/s的条件下,奥氏体完全转化为马氏体。因此将Q&P热处理过程物理模拟的冷却速率设定为30 ℃/s。
图2 不同冷却速率淬火后的常温组织
Fig.2 Normal temperature structures after quenching at the cooling rates of 1 ℃/s (a), 2 ℃/s (b), 5 ℃/s (c), 10 ℃/s (d), 30 ℃/s (e) and 50 ℃/s (f)
无外力作用的模拟实验设备为DIL805A型淬火相变热膨胀仪,实验方案如图3a所示。试样尺寸为10 mm×4 mm×1.2 mm,试样在热膨胀仪中被整体辐射加热,整个热循环实验过程在N2气氛环境下完成。对于考虑应力影响的热-力循环实验,选用的设备为Gleeble-1500热-力模拟试验机。试样为板状试样,有效长度为42 mm,试样长度方向上中点位置焊接热电偶对温度进行测量。采用Smartlab X射线衍射仪(XRD)定量测试经过不同淬火温度处理的试样在室温下的残余奥氏体含量,Cu靶,工作电压40 kV,工作电流150 mA,探测器使用Ni滤波片,扫描速率2°/min,扫描范围47°~93°。
图3 热膨胀实验及相变动力学实验方案
Fig.3 Schemes of thermal expansion experiment (a) and phase change kinetics experiment (b) (Tq—quenching temperature)
残余奥氏体体积分数采用对比法[36]计算,马氏体选用(200)和(211) 2个晶面,奥氏体选用(200)、(220)、(311) 3个晶面,分别进行配对组合。残余奥氏体含量(
式中,
相变动力学模型的确定。因为Q&P热处理过程涉及2次淬火,因此应分别进行实验确定,如图3b。
马氏体相变过程属于非扩散型相变,其相变动力学描述中使用最广泛的是唯象的Koistinen-Marburger (K-M)方程[37]。方程表达式如下:
式中,
相变塑性方程的确定。由于需要外载荷使试样产生相变塑性应变,因此热-力循环实验在Gleeble 1500热-力模拟试验机上进行,采用定载荷实验研究相变塑性[40,41]。试样由室温经过10 ℃/s的升温速率加热至950 ℃,保温300 s使其充分奥氏体化,随后以30 ℃/s的冷却速率进行快速冷却至室温。当温度降至450 ℃时对试样两端施加轴向载荷,载荷水平为20~100 MPa共5个。使用引伸计记录试样正中位置热电偶焊接处的试样宽度方向位移。加热冷却及加载过程如图4所示。相变塑性方程选用Greenwood-Johnson模型(由Greenwood和Johnson于1965年提出[42],在相变塑性研究中得到了广泛应用[43,44]),其表达式为:
图4 相变塑性实验方案
Fig.4 Experimental scheme of phase change plasticity
式中,
类蠕变应变模型的实验确定。Q&P热处理过程的分配阶段,是指第一次淬火形成马氏体与奥氏体双相组织后,再次加热并在分配温度下进行保温,以完成C扩散的热处理过程。广义上这个过程也可看作是对材料的一种时间较短的低温回火过程。刘庄[45]和许学军等[46]指出,一般的低合金钢的回火过程在290~400 ℃温度范围内析出的碳化物合成为较大的球状微粒,使材料表现出软化,在回火时间足够长的情况下会发生体积的收缩,内应力也出现减小。但是,由于工艺目标的不同,Q&P热处理的分配过程相比于常规的回火过程存在一些差异[47],首先是保温温度明显低于回火过程,另外Q&P热处理的保温时间多以分钟计,时长远短于以小时计的回火过程。尽管两者在工艺条件上存在差异,但为精确描述Q&P热处理过程的材料变形行为,本工作将回火过程对材料变形的研究思路应用于Q&P热处理过程。
利用热膨胀仪进行不同分配温度下的Q&P热处理实验,加热冷却制度如图5所示。将试样以10 ℃/s的速率加热至950 ℃并保温300 s,淬火至260 ℃保温5 s后依次加热至350、375、400、425和450 ℃的分配温度保温200 s。利用轴向引伸计记录试样的轴向位移。
图5 不同分配温度的Q&P热处理实验加热冷却制度
Fig.5 Experimental heating and cooling system of Q&P heat treatment with different distribution temperatures
对于热处理过程的材料总应变,多数学者在考虑构建温度场、组织场、应力场的三场耦合数值模拟时对其进行了加法分解[48]。在考虑应力、相变及温度变化的前提下,总应变(
式中,
对于材料未发生相变也未发生屈服的热循环过程,材料变形只包含热胀冷缩及弹性变形2项,总应变分解为:
通过合理设计物理模拟方案,可以运用混合法则将分应变从总应变中分离出来,再利用各自的数学模型分别确定模型参数,从而为数值模拟奠定基础。
当经过热处理过程的材料是由多相结构组成时,可以假设材料参数(
式中,
对于热应变和相变应变关键参数的获得,首先关注第一个加热冷却过程,如图6a所示。在加热阶段,材料由初始组织转变为奥氏体组织,在奥氏体化过程中发生了体积变化(如图6a中AB段所示)。在降温阶段,材料由奥氏体组织转变为马氏体组织,在马氏体转变过程中伴随了体积膨胀(如图6a中DE段所示)。马氏体转变开始点(Ms) (图6a中D点)采用极值法进行确定,对于本工作的研究对象QP980高强钢,
图6 无应力淬火及回火过程轴向应变随温度变化的关系曲线
Fig.6 Relationships between axial strain and temperature during stress-free quenching and tempering (Ms—martensite transformation start temperature)(a) the first quenching process (b) the second quenching process
第二个加热冷却过程中,由于经过第一个加热冷却后,Q&P钢中组织已完全转变为马氏体,因此在400 ℃的温度下保温200 s属于马氏体的低温回火过程。回火马氏体冷却至室温过程的轴向应变变化情况见图6b。将其线性拟合即为回火马氏体的热膨胀系数
得到奥氏体、马氏体组织的热膨胀系数后,即可求得马氏体转变膨胀系数(
对于低碳钢的Q&P热处理过程,第一次冷却至淬火温度(
图7 第一次淬火过程马氏体体积分数(
Fig.7 The relationship between martensite volume fraction (
由于分配过程中马氏体体积分数未发生明显变化,因此第一次淬火结束时,未转变奥氏体的体积分数即为第二次淬火过程马氏体转变的初始值。
将由K-M公式计算得到的未转变奥氏体体积分数理论值与实验测得的室温下残余奥氏体体积分数实测值做差,其差值即为第二次淬火的新生马氏体体积分数,如图8所示。
图8 不同淬火温度下第二次淬火过程前后的组织变化
Fig.8 Microstructure changes before and after the second quenching process with different quenching temperatures
对不同淬火温度下的新生马氏体体积分数进行二次拟合,得到了不同淬火温度的Q&P热处理工艺第二次淬火过程中新生马氏体体积分数与
式(9)的意义在于建立了第二次淬火新生马氏体体积分数与淬火温度的关系,从而可以更为精确地确定新生马氏体相变的动力学方程。在K-M方程的基础上进行改进,得到新生马氏体相变动力学模型如式(10),在100~300 ℃范围内的计算结果如图9所示。基于XRD实测结果,对不同淬火温度下的室温残余奥氏体体积分数进行四次拟合,得到二者的关系式如式(11)。
式中,
图9 不同淬火温度Q&P热处理第二次淬火过程的相变动力学曲线
Fig.9 Phase change kinetics curves of the second quenching process with different quenching temperature Q&P heat treatment
马氏体相变过程在不同外载作用下的宽向应变如图10所示。
图10 外载作用下马氏体相变过程的宽向应变
Fig.10 Wide-direction strain of martensite transformation process under external loading
相变塑性系数(k)可表示为:
式中,
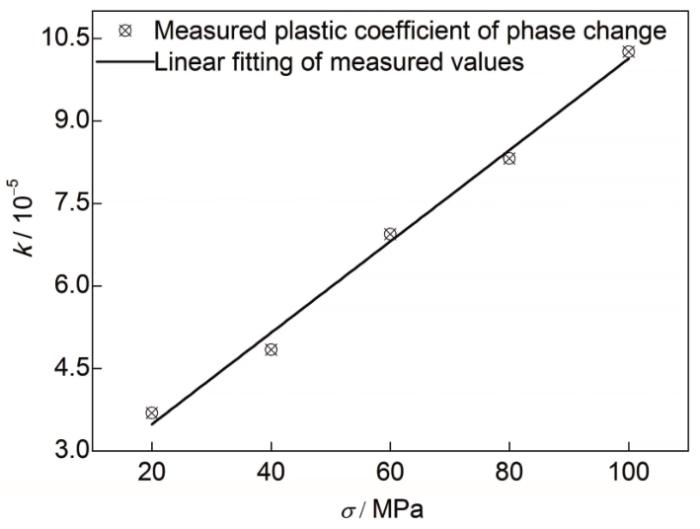
根据式(12)求得k,并将其与
图11 相变塑性系数(k)实测值及线性拟合
Fig.11 The measured value of phase change plasticity coefficient (k) and linear fitting (σ—stress in the same direction as phase transformation plastic strain)
最终得到实验材料的相变塑性模型如下式所示:
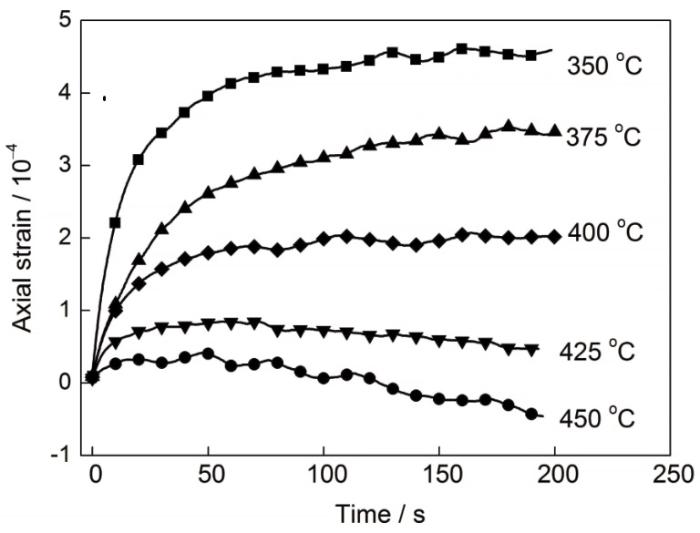
观察试样轴向应变在Q&P热处理不同分配温度下保温过程的变化情况,发现其随分配温度和时间呈现规律性变化,如图12所示。保温过程参数见图5所示。在这200 s的等温分配过程中,试样两端无外力作用,温度也保持恒定,因此在同一温度下测得的轴向应变成为了只与时间有关的函数。而轴向应变数量级为10-4,相较于Q&P热处理的2次淬火和一次升温过程的应变,在数量级上接近,因而考虑将该等温过程的应变进行量化,通过有限次温度的实验形成唯象方程以模拟在350~450 ℃范围内的常见工业Q&P热处理场景,使有限元模型对材料变形的预测更为精确。
图12 不同分配温度下Q&P热处理分配过程中的轴向应变
Fig.12 Axial strain during Q&P heat treatment with different distribution temperatures
分析轴向膨胀的规律可知,在分配温度不高于400 ℃时,试样的轴向应变随着时间增大,在50 s内变化最快;在分配温度高于400 ℃时,轴向膨胀呈上升后略下降的趋势。从分配阶段结束时的总应变看,分配温度越低,轴向应变越大。在350、375、400、425、450 ℃分配温度下保温后的轴向应变分别为4.589×10-4、3.464×10-4、2.019×10-4、4.705×10-5、-4.443×10-5。保温过程中材料的变形应在数值模拟中予以考虑,否则将使模拟结果准确性下降。
在热处理过程数值模拟中,一般将总应变增量分解为热应变、弹性应变、塑性应变、相变应变、相变塑性应变5个应变分量增量,即等于该5个应变分量的增量之和,如式(4)所示。因此,在Q&P热处理的等温分配过程中,上述5项应变分量增量均为0,所以总应变也应为0,但这与实验观测到的情况相悖。因此本工作为更精确地模拟该热处理过程,反映不为0的应变增量,假设其是一种唯象的类蠕变应变,用于表示分配过程中材料的体积变化。考虑分配温度及分配时间对该类蠕变(εc)的耦合影响,其表达式为:
式中,n、m、l为类蠕变应变指数项,对于本工作的研究对象QP980高强钢,其值为4;
针对实验测得轴向应变,取时间区间5~195 s内11个时间节点的分配温度与对应应变值,进行三次多项式拟合,结果如表1所示。可见判定系数R2值处于0.922~0.998之间,表示拟合精度较好。
表1 约化温度系数的三次多项式拟合结果
Table 1
Time / s
R2
对各系数与时间的对应关系再次进行多项式拟合,得到类蠕变应变的方程待定系数如表2所示。
表2 QP980高强钢类蠕变应变方程系数
Table 2
Coefficient value
Coefficient value
Coefficient value
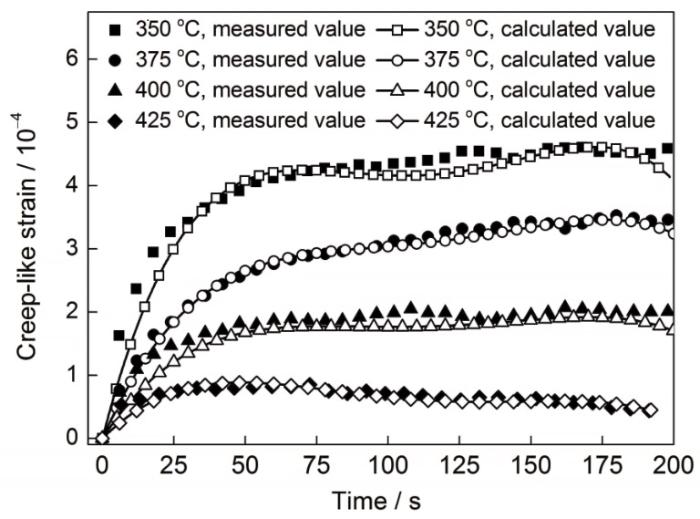
对于QP980高强钢,将本工作提出的唯象的类蠕变应变方程计算值与实验得到的实测值进行对比,如图13所示。可见,唯象的类蠕变应变方程能够较准确地预测在Q&P热处理分配过程材料的变形行为。
图13 类蠕变应变计算值与实测值对比
Fig.13 Comparison of the calculated and measured values of creep-like strain
综合考虑相变过程中相变膨胀、相变塑性影响、温度场变化过程中的热应变以及前文观测到的Q&P热处理等温分配过程中类蠕变应变的影响,材料的总应变可以进行加法分解为6个应变分量之和,写成增量形式为:
式中,
各应变增量的表达式如式(17)~(21)。
式中,αI、βI分别为第I相的热膨胀系数和相变膨胀系数,本工作中I=0为奥氏体,I=1为马氏体,I=2为回火马氏体;
针对QP980钢的热处理过程,以上各式中待定系数已通过实验研究得到,相体积分数
分析Q&P热处理过程的等温分配过程时(如图5所示),存在如下条件:试样两端无外力作用,温度无变化且无相变产生。因此,式(16)中:
使得
此时实验测得的材料总应变变化等于类蠕变应变的变化。根据温度场、组织场和应力应变场的三场耦合原理以及上述的增量本构模型,本工作基于对商业有限元软件ABAQUS用户子程序UMAT的二次开发,建立了Q&P热处理过程的数值仿真模型。
在对数值模型进行求解的过程中,对于各场间的耦合关系通过参数矩阵及载荷向量进行实现,非线性问题通过ABAQUS软件的迭代算法解决。在对各场计算的过程中,温度场与应力应变场的耦合过程体现在温度变化所引起的热应变,温度场与组织场的耦合体现在相变动力学的计算,组织场与应力应变场的耦合体现在相变应变及相变塑性应变。
为验证数值仿真模型计算结果的准确性,在Gleeble1500热-力模拟试验机上对标准试样进行外载作用下的Q&P热处理实验,加热冷却及加载制度如图14所示。首先将试样加热至950 ℃并保温300 s使其完全奥氏体化,然后以30 ℃/s的冷却速率冷却至260 ℃,冷却开始的同时对试样两端施加20 MPa外载,该过程为第一次淬火;而后将试样再次加热至分配温度400 ℃并保温200 s完成碳分配过程;最后第二次以30 ℃/s的冷却速率第二次淬火至室温。
图14 Gleeble上Q&P热处理实验加热冷却加载制度
Fig.14 Loading system of heating and cooling for Q&P heat treatment experiments on gleeble
由于采用宽向引伸计C-Gauge测量试样宽度方向变形,无需考虑非均热区影响,因此在建立数值仿真模型的验证模型时,建立等温的均热段三维有限元模型即可对试样变形进行仿真计算,试样均热段的有限元模型如图15所示。
图15 模型验证实验试样均热区有限元模型
Fig.15 Model validation finite element model of heat distribution of test samples
将有限元模型的宽度方向总应变与实验测得宽度应变随温度的变化在Q&P热处理的各阶段逐一对比,如图16所示。将材料相体积分数随时间的变化过程分阶段表示于图17。
图16 Q&P热处理过程各阶段试样变形模拟值与实测值对比
Fig.16 Comparisons between simulated and measured deformations of samples in different stages of Q&P heat treatment process
(a) first quenching process (b) partitioned heating process
(c) partitioned holding process (d) second quenching process
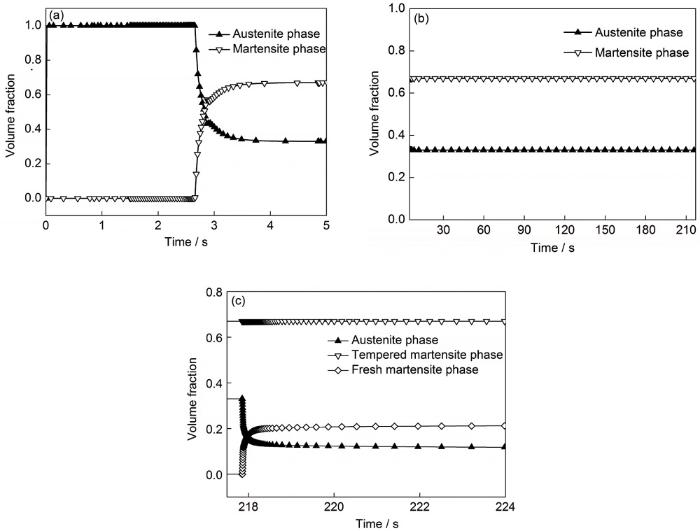
图17 Q&P热处理各阶段相体积分数随时间的变化
Fig.17 Variations of phase volume fraction with time in Q&P heat treatment stages
(a) first quenching process (b) distribution process (c) second quenching process
经过对比,本工作所建立的数值仿真模型对试样应变的计算值与Gleeble试验机上所得实测值能够较好吻合,这说明数值仿真模型能够较为准确地预测材料在Q&P热处理中的变形。
(1) 测定了典型Q&P高强钢——商业QP980钢的合金成分;通过Gleeble热-力模拟实验获得了其连续冷却转变曲线(CCT曲线),确定了后续实验的冷却速率为30 ℃/s。对QP980高强钢的无应力淬火过程进行物理模拟,得到材料马氏体相变开始点温度,确定了各相的热膨胀系数和相变膨胀方程。
(2) 对QP980高强钢在不同淬火温度下的Q&P热处理过程进行物理模拟。通过XRD实验测得常温组织残余奥氏体含量,建立了考虑淬火温度影响的Q&P热处理第二次淬火的相变动力学方程;利用K-M方程描述了第一次淬火的相变动力学。利用Gleeble热-力模拟试验机对不同应力状态下的马氏体相变过程进行物理模拟,建立了Greenwood-Johnson形式的马氏体相变塑性方程。
(3) 研究了Q&P热处理过程等温分配阶段的材料变形规律,针对其间的体积变化,提出一种唯象的耦合温度与时间影响的类蠕变应变模型,基于实验数据对方程系数进行求解。经对比,考虑类蠕变应变模型对QP980高强钢在分配过程变形的预测值与实测值吻合良好。基于ABAQUS有限元软件进行用户子程序二次开发,构建了Q&P热处理过程中的组织场、温度场、应力应变场三场耦合数值仿真模型,并通过Gleeble试验机对模型进行了实验验证,结果表明数值模拟结果与实验结果吻合良好。
1 实验方法
图1
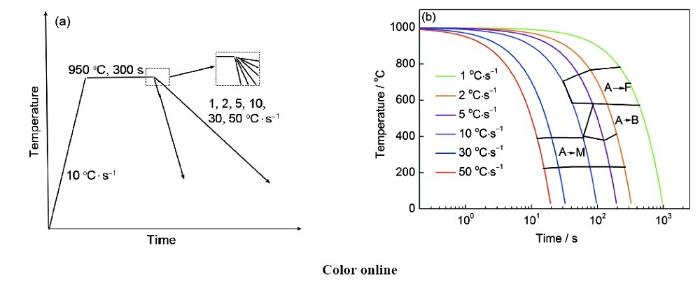
图2
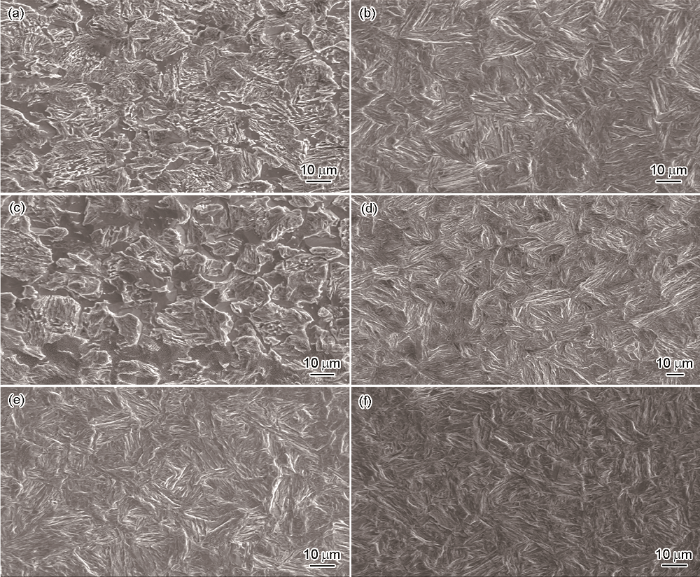
图3
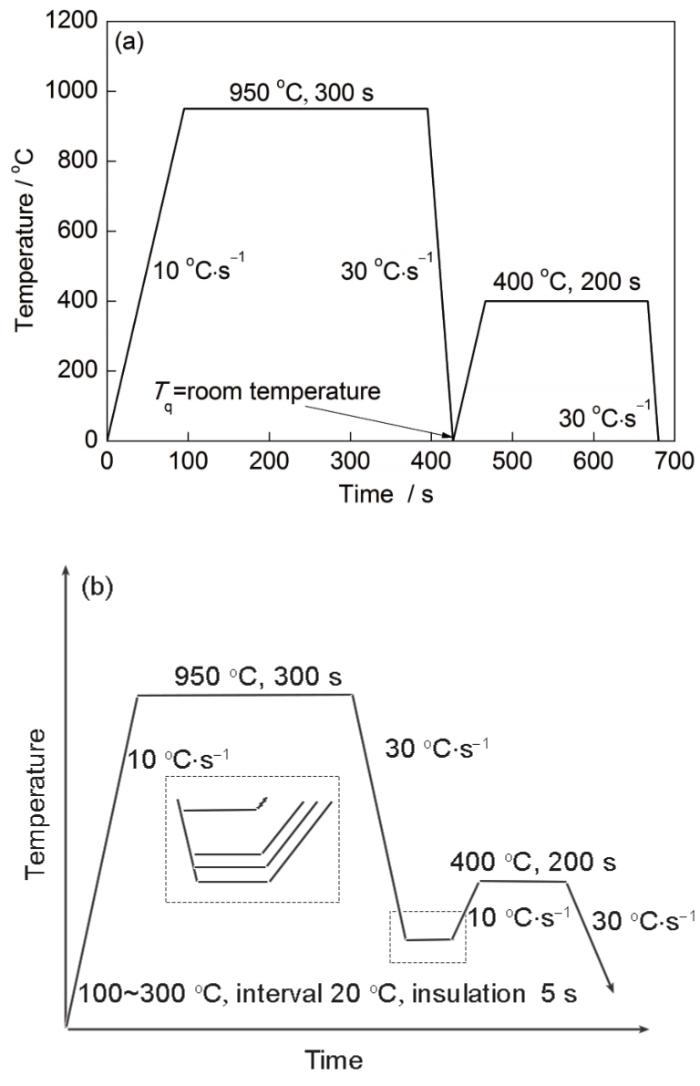
图4
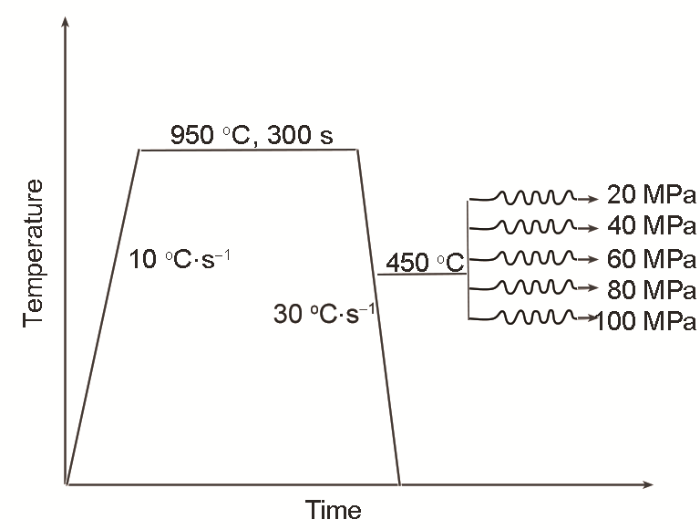
图5

2 实验结果与分析
2.1 应变的分离
2.2 热应变与相变应变方程的确定
图6

2.3 相变动力学模型的确定
图7

图8
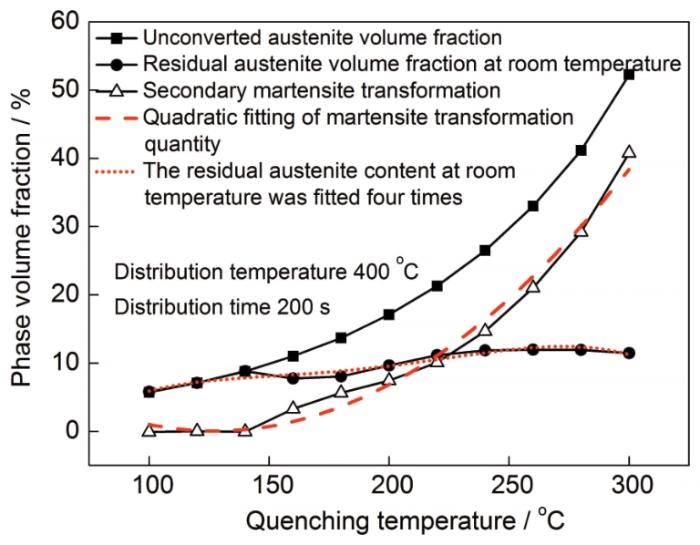
图9

2.4 相变应变方程的确定
图10

图11
2.5 类蠕变应变方程的确定
图12
Coefficient of primary temperature term
Coefficient of quadratic temperature term
Coefficient of cubic temperature term
5
2.98×10-4
-6.26×10-4
4.64×10-4
0.9220
25
4.20×10-4
-5.74×10-4
4.73×10-4
0.9622
45
3.56×10-4
-1.87×10-4
2.06×10-4
0.9663
65
3.23×10-4
-7.66×10-4
9.35×10-5
0.9900
85
1.85×10-4
4.02×10-4
-1.69×10-4
0.9953
105
1.65×10-4
5.59×10-4
-3.01×10-4
0.9964
125
6.53×10-4
8.23×10-4
-4.44×10-4
0.9984
145
-4.74×10-4
1.07×10-3
-6.29×10-4
0.9915
165
3.53×10-5
9.34×10-4
-5.21×10-4
0.98288
185
-1.16×10-4
1.39×10-3
-8.35×10-4
0.9769
195
-8.92×10-5
1.28×10-3
-7.49×10-4
0.96565
Coefficient of equation
Coefficient of equation
Coefficient of equation
p1
2.65×10-5
q1
-4.16×10-5
w1
3.26×10-5
p2
-5.20×10-7
q2
1.03×10-6
w2
-7.69×10-7
p3
3.44×10-9
q3
-7.17×10-9
w3
5.31×10-9
p4
-7.65×10-12
q4
1.62×10-11
w4
-1.20×10-11
图13
3 Q&P热处理过程温度-组织-应力场的有限元实现
3.1 弹塑性增量本构模型
3.2 数值仿真模型的实验验证
图14

图15
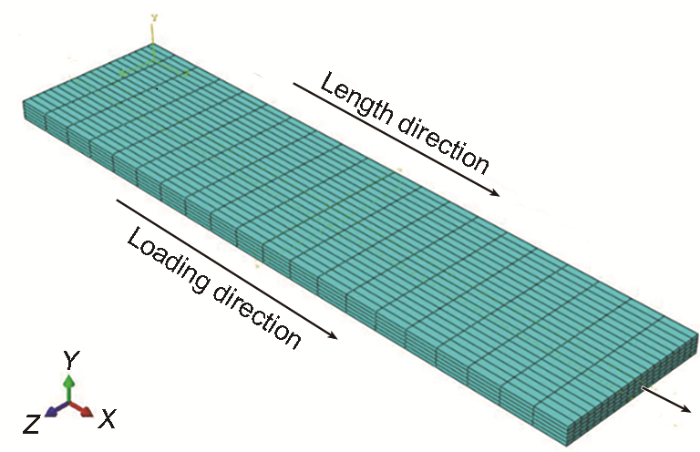
图16
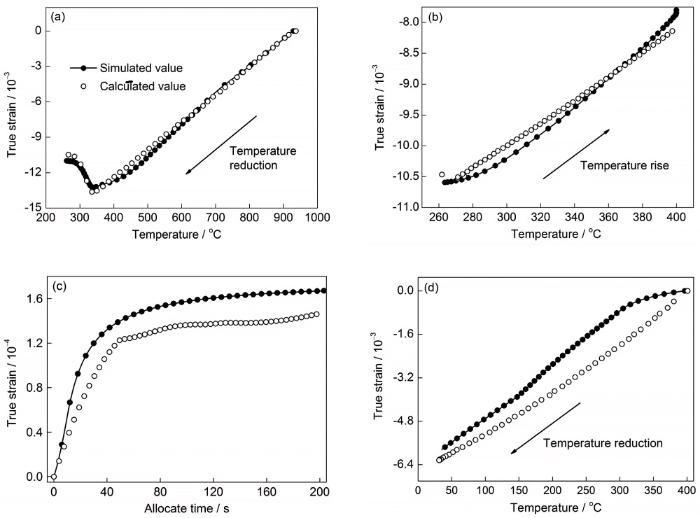
图17
4 结论
来源--金属学报







 沪公网安备31011202020290号
沪公网安备31011202020290号
