分享:蠕变对焊后热处理残余应力预测精度和计算效率的影响
重庆大学材料科学与工程学院 重庆 400044
基于MSC. Marc软件平台,开发了考虑蠕变效应的热-弹-塑性有限元计算方法。采用该方法模拟了Q345平板接头TIG重熔焊接过程和焊后热处理过程中的应力场,并重点研究了焊后热处理过程中蠕变效应对焊接残余应力的影响,基于数值模拟结果研究了焊后热处理消除残余应力的机理。同时,采用盲孔法实测了焊接及热处理后平板接头的残余应力,并与数值模拟结果进行了对比。此外,还探讨了2种不同的蠕变模型对焊后热处理残余应力计算精度的影响,针对Q345低合金高强钢,提出了一种简易高效、适合于工程应用的蠕变模型。结果表明:数值模拟得到的残余应力与实验值吻合良好,验证了所开发的集成计算方法的有效性。热处理计算过程有必要考虑材料的蠕变效应,否则会严重高估热处理后的残余应力。采用本工作提出的简易蠕变模型,在较少损失计算精度的前提下可使计算效率提高10倍左右。
关键词:
低合金高强钢因强度高、塑韧性好、成本低廉等优点而被广泛应用在桥梁、建筑、压力容器及船舶等工程结构中[1,2,3],其连接方式大多采用密封性好、接头强度高、结构设计灵活性大的焊接加工工艺[4]。但由于焊接工艺的局部高密度能量快速加热特点,使钢结构在经历焊接温度循环后不可避免地会产生残余应力与变形。残余应力的存在会促使构件服役过程中产生脆性断裂、应力腐蚀裂纹以及降低构件的疲劳强度[5,6]。当构件受压时,焊接压缩残余应力与工作应力相叠加达到一定数值后,可使焊接结构产生局部失稳[7,8]。焊接残余应力的存在将严重影响焊接结构件的使用性能,因此对焊接残余应力的控制是工艺设计制造过程中必须要考虑的问题[9,10,11]。
热处理法是一种能较充分地消除焊后残余应力的有效方法[12,13]。余磊[14]研究了焊后热处理对窄间隙埋弧焊接头残余应力的消除情况。结果表明,焊后热处理能有效降低焊接残余应力以及改善应力分布。Venkata等[15]以P91钢平板对接接头为研究对象,利用数值模拟方法研究了不同的热处理工艺参数对残余应力的消除情况。基于理论分析可知,焊后热处理中有3个主要因素会对焊接残余应力的大小与分布有影响:(1) 加热到热处理温度后材料会发生软化(即屈服强度和弹性模量都降低);(2) 材料在热处理过程中力学性能(尤其是屈服强度)会发生变化;(3) 蠕变效应。但目前对热处理法消除残余应力的机理尚缺乏定量而系统的研究,尤其是对蠕变效应的研究多集中在高温服役环境下对材料性能的影响。Dong等[16]以P91和2.25CrMo钢为对象,研究了焊后热处理去除残余应力的机理。结果表明,材料高温的蠕变效应在残余应力的消除中发挥了重要的作用。本课题组[17]在未考虑蠕变的情况下,采用数值模拟手段研究了异种钢对接接头的焊后热处理对残余应力的影响。结果表明,焊后热处理对消除异种钢接头的残余应力作用十分有限。因此,在热处理过程中考虑蠕变效应对焊接残余应力的影响是十分有必要的。然而,目前蠕变效应在焊后热处理过程中的作用机理及影响还鲜有系统的研究。对于数值模拟而言,在焊后热处理的数值模拟过程中,如果能将这一因素考虑进去,将提高数值模拟方法对焊接及热处理后残余应力的预测精度,同时也对工艺生产具有十分重要的指导意义。
本工作基于MSC. Marc软件平台,开发了考虑蠕变效应的“焊接+热处理”有限元集成计算方法。采用开发的计算方法模拟了低合金高强钢Q345平板接头钨极氩弧焊(TIG)重熔的焊接过程和焊后热处理过程,分析其温度场和应力场,重点研究了热处理消除焊接残余应力的机理及蠕变效应在焊后热处理过程中对焊接残余应力的影响规律。同时,通过盲孔法分别实测了焊后和热处理后平板接头的残余应力,通过模拟结果与实验结果的对比来验证本工作所开发的有限元模型的有效性。此外,本工作还探讨了焊后热处理过程中在不同阶段(加热、保温、冷却)考虑蠕变效应对残余应力计算精度和计算效率的影响,针对Q345低合金高强度钢,进一步提出了一种简易而高效的蠕变模型,在保证计算精度的情况下大幅节约计算时间。
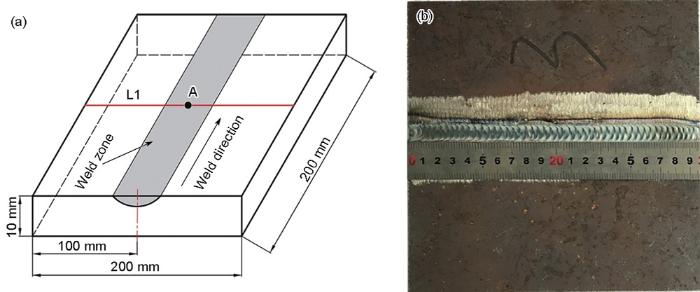
实验对象为2块几何尺寸为200 mm×200 mm×10 mm的Q345低合金高强钢,如图1a所示。其主要化学成分(质量分数,%)为:C 0.15,Si 0.65,Mn 1.47,Ni 0.007,Cr 0.034,Cu 0.029,V 0.001,Fe余量。先采用TIG焊分别在2块试件表面重熔一道约10 mm宽的焊缝(图1b),焊接过程中不添加焊丝,采用的焊接工艺参数为:焊接电流189 A,焊接电压13 V,焊接速度2.4 mm/s,焊接线能量870 J/mm。焊接完成后,其中一块试件直接进行残余应力的测量,另一块试件进行焊后热处理,再测量其残余应力。
图1 试件几何尺寸及实物照片
Fig.1 Shape and dimension of mock-up (a) and picture of mock-up (b)
将焊后热处理的试件放在Nabertherm加热炉里进行热处理,采用的热处理温度为600 ℃,保温时间2 h,热处理温度循环曲线如图2所示。加热过程中炉膛气氛与试件之间的热交换用Newton定律[18]来描述:
式中,
图2 焊后热处理的温度循环曲线
Fig.2 Thermal cycle curve of post weld heat treatment (PWHT) process
为减小试件内部的温度梯度,加热过程中设定加热速率为5 ℃/min,冷却过程采取随炉冷却的方式,试件在加热炉内冷却到室温(25 ℃)后取出,从而避免在热处理过程中由于工件内部存在较大的温度梯度产生新的附加应力。
为验证本工作提出的有限元方法预测残余应力的有效性,采用盲孔法分别测量焊后和热处理后2块不同试件表面上沿图1所示的试板中央截面直线L1上的残余应力,包括横向残余应力(垂直于焊接方向的残余应力)和纵向残余应力(平行于焊接方向的残余应力)。关于本工作采用的盲孔法测量焊接残余应力的原理见文献[19]。应变片的位置分布在焊缝附近,如图3所示。为了方便起见,这里把焊缝中心线作为Y方向的零点位置,这样就可以根据各个应变片的中心与焊缝中心线的距离来确定各个测试点的Y坐标值。打孔深度和孔径大小分别为2.0和1.5 mm。
图3 残余应力测量位置
Fig.3 The locations of residual stress measurements on top surfaces
(a) as weld (b) PWHT
本工作基于有限元软件MSC. Marc,开发了用于计算试件“焊接+热处理”过程残余应力的热-力耦合计算方法。为了保证计算精度,数值模拟过程中考虑了材料参数随温度的变化,Q345钢的高温热物理性能参数[20]和力学性能参数[21]如图4所示。由于焊接过程中没有添加焊接材料,所以在有限元计算过程中焊缝区与母材采用完全相同的材料参数。同时,由于Q345钢属于低合金钢,根据国际焊接学会推荐的公式[22]计算可知其C当量(质量分数,%)为0.38,可以推测固态相变对焊接残余应力的影响较小,因此在进行热-力耦合分析时忽略了固态相变对应力形成过程的影响[23]。此外,由于Q345钢的加工硬化不明显,因此计算过程也忽略了加工硬化效应[23]。焊接残余应力计算完成后,以计算得到的残余应力作为初始应力状态,来进行焊后热处理过程的模拟计算。
图4 Q345钢的热物理性能参数[20]和力学性能参数[21]
Fig.4 Temperature-dependent thermal-physical[20] (a) and mechanical[21] (b) properties of Q345 steel
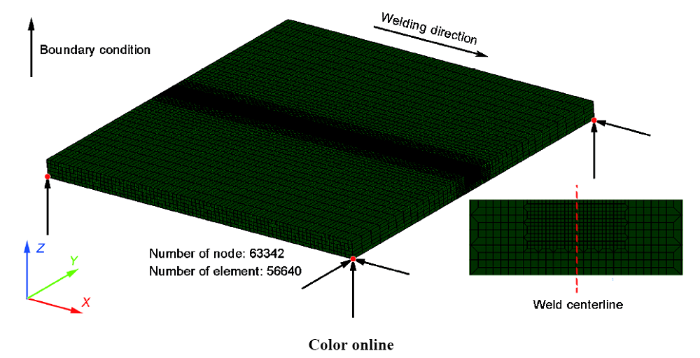
为了准确预测焊后及热处理后试件的残余应力,本工作建立了与实际试件尺寸完全相同的有限元模型,如图5所示。由于单道重熔后试件几乎没有余高,因此在建立有限元网格模型时忽略了焊缝余高。模拟焊接过程与模拟热处理过程所用的网格模型完全相同。模型中的单元数为56640,节点数为63342。为兼顾计算精度和计算效率,在焊缝及其附近温度梯度较大的区域网格划分得比较致密,而远离焊缝区域的网格划分得相对稀疏,采用的单元类型均为8节点6面体砖块单元 [24]。由于在实际焊接过程和热处理过程中工件均处于自由状态,因此在进行有限元计算时,仅仅在3个节点上采用了防止刚体位移的拘束条件,如图5所示。
图5 3D有限元模型
Fig.5 3D FEM model (FEM—finite element method)
在焊接过程中,为了模拟TIG焊电弧的热输入,采用的热源模型为Goldak等[25]提出的双椭球移动热源模型,该模型中椭球前、后半部分的热流密度(qm和qr)分布如下:
式中,Q=ηUI,为焊接热量(其中,U为焊接电压,I为焊接电流,η为焊接热效率,取η=0.75[26]);af、ar、b和c为椭球形状参数;ff和fr为前、后椭球热量分布函数,且ff+fr=2,在本研究中,取
在应力计算过程中,采用的网格模型与热分析时完全相同。弹性应变计算遵循各向同性Hookean定律,塑性应变计算采用Von-Mises准则。在未考虑相变的情况下,材料的总应变(εtotal)可由下式来描述:
式中,εe为弹性应变;εp为塑性应变;εth为热应变;εcr为蠕变应变。
在热处理过程中,考虑了材料的蠕变效应。焊接过程由于是快速加热随后又快速冷却,材料在高温阶段的时间很短暂,因此焊接过程没有考虑材料的蠕变效应。
将焊接过程计算得到的残余应力作为初始条件,进行后续的焊后热处理模拟计算,二者采用相同的有限元模型。由于试件板厚较薄,热处理过程中的加热和冷却速率都相对较慢,故可近似认为工件内部不存在温度梯度,因此,本工作在模拟热处理过程时采用了直接在有限元模型的每个节点上施加与热处理炉相同的温度热循环,来模拟研究在热处理过程中的温度变化,如图2所示。
如前言所述,焊后热处理之所以能消除残余应力,主要有3个原因,即材料加热到热处理温度后要发生软化(屈服强度和弹性模量降低),蠕变效应以及材料在热处理过程中力学性能(尤其是屈服强度)会发生变化。在模拟焊后热处理过程时,重点考虑了前2个因素,没有考虑因热处理(退火)导致材料屈服强度降低这一因素的影响。
对蠕变效应的考虑是因为热处理过程时间较长,加上试件焊后存在较大的残余应力,从理论上分析,对于Q345低合金高强钢而言,热处理过程中的蠕变效应会对焊后残余应力有显著影响。热处理计算过程,假定材料的蠕变行为服从Fields & Fields蠕变方程[27]:
式中,
该蠕变模型可以模拟第一和第二蠕变阶段,与实际的热处理过程比较接近,从而使模拟计算更加精确。由于Q345钢在300 ℃以下几乎不发生蠕变,因此设置300 ℃以下的蠕变参数a为0,热处理过程其它温度段的蠕变参数[28]表示如下:
式中,T为热处理温度。
最后通过Fortran语言编写蠕变子程序,在热处理计算过程中供MSC. Marc软件调用。由于蠕变过程与时间相关,且加热和冷却阶段的不同时刻试件的温度和应力都在不断发生变化,因此为了计算的准确性,计算过程每迭代一次设置的时间步长不能太大,力学计算时采用自适应时间步长进行计算,且初试时间步长设为0.0001 min。
为了定量比较热处理前后的残余应力变化情况以及定量讨论热处理过程中材料蠕变效应对焊接残余应力的影响规律,本工作设计了4个有限元计算案例,如表1所示。Case A只考虑焊接过程,而完全不进行热处理,用于计算焊接残余应力;Case B同时考虑焊接过程和热处理过程,在热处理过程中仅考虑材料的软化效应而不考虑蠕变效应;Case C同时考虑焊接过程和热处理过程,在热处理过程中,除了考虑软化效应外,还考虑了蠕变效应,需要强调在Case C中,仅在热处理保温阶段考虑了蠕变效应,而在加热和冷却过程中均不考虑蠕变效应;与Case C相对应,Case D在加热、保温和冷却3个阶段中均考虑了材料的蠕变效应。本工作的4个计算案例均在同一台16CPU的计算机(CPU:i9-9900K,3.6 GHz,RAM:32 GB)上完成。
表1 数值模拟计算案例
Table 1
限于篇幅,对于温度场的计算结果不做讨论,这里重点讨论残余应力的结果。
图6是4个不同计算案例得到的纵向残余应力分布云图及中央截面焊缝附近的应力分布。由于有限元模型及边界条件是关于X轴对称的,故4个计算案例得到的残余应力的分布也是左右对称的。对比Case A和Case B可知,在不考虑蠕变效应的情况下,通过焊后热处理纵向残余应力的分布形态几乎没有发生变化,即在焊缝附近区域纵向残余应力峰值较大,且为拉应力,随着与焊缝中心线距离的增加逐渐减小并变为压应力;但是经过热处理后无论是纵向拉伸应力还是压缩应力,它们的峰值均有所降低,在Case B中,残余应力的降低仅仅是因为热处理过程中材料发生软化所致。
图6 4个不同计算案例得到的纵向残余应力分布云图及中央截面焊缝附近的应力分布
Fig.6 Contours of longitudinal residual stress distribution (top) and stress distribution near weld of central section (bottom) from four different computing cases
(a) Case A (as-weld) (b) Case B (as-weld and heat treatment)
(c) Case C (as-weld and heat treatment with holding creep) (d) Case D (as-weld and heat treatment with all creep)
对比Case A、Case B和Case D可知,在考虑热处理过程的蠕变效应时,纵向残余应力无论是分布形态还是数值大小都发生了较显著的变化。热处理过程中考虑蠕变时,Case D的纵向拉伸残余应力的分布区域比Case A和Case B的宽,但应力值有十分显著的下降。比较Case B与Case D可知,热处理过程中考虑蠕变效应后残余应力显著降低,说明Q345钢在热处理过程中蠕变效应对应力松弛的作用十分显著。此外,对比Case C和Case D可知,只考虑保温阶段的蠕变效应与考虑整个热处理过程的蠕变效应得到的纵向残余应力的分布形态基本一致,只是应力的峰值大小略微有些差别,其原因有2个,一个是蠕变参数在热处理温度(600 ℃)以下时比较小,二是加热阶段温度超过300 ℃的时间比较短,同时在冷却阶段由于应力在保温阶段释放比较充分,尽管冷却到300 ℃的时间较长,但残余应力已经比较小了,所以应力进一步释放的驱动力变小。总体而言,Case C和Case D应力峰值大小的差异可以忽略。
图7是4个不同计算案例得到的横向残余应力云图及中央截面焊缝附近的应力分布,4个计算案例得到的横向残余应力也是沿X轴呈左右对称分布。对比分析可知,对于横向残余应力的分布而言,4个不同计算案例得到的应力分布形态基本一致。在Case A中,焊缝附近为横向拉伸应力,随着离焊缝中心线距离的增加应力逐渐减小,最后变为横向压缩应力,焊缝的始终端处由于几何端部效应的影响存在较大的压缩残余应力。经过热处理后,横向残余应力的分布形态没有显著变化,但应力值比焊态(Case A)下要小很多。对比Case A和Case B,横向残余应力的峰值由192 MPa减小到159 MPa;而在考虑蠕变的Case C和Case D中,它们的横向残余应力峰值都降到了67 MPa。由此可知,蠕变效应在热处理过程中消除残余应力是一个相当重要的因素,不能忽略。对比Case C和Case D可知,二者残余应力的分布及数值没有显著差别,从中央截面上的应力分布来看,二者仅仅是在拉伸应力分布的区域上有一些细微的差异。
图7 4个不同计算案例得到的横向残余应力分布云图及中央截面焊缝附近的应力分布
Fig.7 Contours of transverse residual stress distribution (top) and stress distribution near weld of central section (bottom) from four different computing cases
(a) Case A (b) Case B (c) Case C (d) Case D
为了验证基于MSC. Marc有限元软件所开发的残余应力计算方法的可靠性,本工作在进行了相应的焊接和热处理实验之后,采用盲孔法测量了焊态和热处理后的残余应力。
提取了通过有限元方法(FEM)计算得到的试件上表面沿直线L1 (L1的位置如图1所示)上的纵向和横向残余应力,如图8所示,同时通过盲孔实验(Exp.)测得的应力值也被绘制在该图中。由于焊后的残余应力沿X轴呈对称分布,在残余应力测量点较少的情况下,为了能较好地展示应力分布的形态,本工作将实验测量结果对称后全部放在了Y轴的右边,且模拟结果的应力分布线图也只展示了一半的结果。需要强调的是,虽然应变片的粘贴位置不在同一条直线上,但由于应变片粘贴位置集中在整条焊缝的中间部位,而该部位的应力分布比较稳定,因此将实验测量的数据放在了一条直线上。
图8 焊接完成后沿直线L1上的纵向和横向残余应力分布
Fig.8 Longitudinal (a) and transverse (b) residual stress along L1 line in Fig.1a after welded (Case A)
由图8可知,无论是沿L1的纵向残余应力还是横向残余应力,通过数值模拟方法得到的结果与实验结果相比无论是数值上还是分布上都吻合较好,从而验证了本工作所开发的计算方法的有效性。从图8中可知,焊后试件上表面焊缝附近区域存在较高的纵向拉伸残余应力,应力峰值达到409 MPa;而上表面的横向残余应力在焊缝附近及远离焊缝中心的区域较小,在距离焊缝中心线12 mm的位置应力最大,达到了112 MPa,考虑对称性从全模型来看,上表面的横向残余应力呈典型的M形分布特征。
为了定量比较Case B、Case C、Case D 3个不同计算案例的计算结果,分别从计算结果中提取了3个不同案例热处理后沿直线L1上的纵向与横向的残余应力,如图9所示。同时,实验测得的应力结果也绘制在此图中。由图9可知,对于沿L1的纵向残余应力和横向残余应力而言,通过Case C、Case D计算得到的结果与实验结果相比无论是数值上还是分布形态上都吻合良好,而Case B由于只考虑了材料的软化效应,其热处理后的残余应力偏大。以上的分析与比较说明2个问题:一是为了保证计算精度,必须要考虑蠕变效应对应力松弛的作用,否则将使计算后的残余应力偏大;二是只考虑保温阶段的蠕变效应与同时考虑整个热处理过程的蠕变效应都能很好地预测热处理后的残余应力,从而证明了可以采用简化算法(Case C)来预测焊后热处理的残余应力。从图9中还可以看出,通过热处理过程只能减小残余应力的大小,不会改变应力的分布形态,而且在应力越大的地方经过热处理后应力下降的幅度也越大。由式(5)知,应力越大蠕变的驱动力也越大,蠕变松弛效应也就越明显。经过热处理后,在考虑蠕变效应的情况下,纵向残余应力峰值从409 MPa降到了79 MPa,降幅约81%;横向残余应力峰值从112 MPa降到了34 MPa,下降了约70%;而不考虑蠕变效应时,纵向残余应力的峰值降到了280 MPa,与热处理前相比仅下降了32%左右;横向残余应力的峰值降到了92 MPa,与热处理前相比只下降了18%左右。
图9 不同计算案例沿直线L1上的纵向和横向残余应力分布
Fig.9 Longitudinal (a) and transverse (b) residual stress along L1 line in Fig.1a (Case B, Case C and Case D)
综上可知,无论是只考虑保温阶段的蠕变效应还是整个热处理过程的蠕变效应,都能很好地预测焊后热处理的残余应力分布情况,而完全不考虑蠕变效应的模型对热处理后的残余应力计算结果偏大;经过热处理后,考虑蠕变效应的模型可使纵向残余应力的峰值下降约81%,横向残余应力峰值下降约70%,而不考虑蠕变效应的模型,只能使纵向残余应力的峰值下降32%左右,使横向残余应力的峰值下降18%左右。基于以上定量比较可知,对于Q345低合金高强钢焊接接头而言,在600 ℃下进行热处理时,蠕变效应相对于材料软化而言对于消除焊接残余应力有更大的贡献。至于造成这种差异的原因及热处理消除残余应力的机理,将会在后续部分进行详细讨论。
为了定量比较Case C和Case D 2个不同案例计算效率的差异,对比了在同一台计算机上先后完成上述2个计算案例所花费的时间,Case C计算完成耗时0.32 h,Case D计算完成耗时3.38 h。结果表明,与考虑整个热处理阶段的蠕变效应相比,仅考虑保温阶段的蠕变效应可使计算效率提高10倍左右。从工程应用角度出发,选择简化模型Case C (仅考虑保温阶段的蠕变)来模拟焊后热处理的残余应力有更高的计算效率,可以大幅减少计算时间。
由理论分析知,在焊后热处理过程中,材料软化(屈服强度和弹性模量降低)、蠕变效应以及材料力学性能(尤其是屈服强度)的变化会对焊接残余应力有影响。虽然材料在经历600 ℃的热处理后屈服强度会有一定程度的降低,但由于本工作重点考虑蠕变效应对应力松弛的作用,同时未实测热处理后材料的高温力学性能,因此,在数值模拟过程中忽略了该因素对残余应力的影响。焊接热处理后残余应力及总的应变可以由下式来描述:
式中,
为了研究不同计算案例热处理过程中残余应力消除程度的差异,分别从Case B、Case C和Case D 3个案例计算结果中提取了试件中央截面上焊缝中心处A点(见图1)纵向应力随时间变化的结果,3个计算案例中A点的残余应力-时间曲线如图10所示。由图10可知,在加热阶段,3个案例中A点的纵向残余应力随加热温度的升高都在不断地降低,在考虑蠕变效应的情况下,Case D中A点纵向应力下降速率比Case B和Case C的都快。对于Case B和Case C而言,这一阶段的应力下降是由于材料的屈服强度随温度升高而降低,同时材料的弹性模量也随温度的升高而降低所致。在Case D中不仅有上述因素,同时由于蠕变效应对应力的释放也有一定的贡献,因此Case D中A点纵向残余应力下降速率比Case B和Case C的都快。在保温阶段,当不考虑蠕变作用时(Case B),A点的纵向残余应力保持不变,而Case C和Case D中A点的纵向残余应力仍在不断减小,随着保温时间增加,应力的变化率逐渐降低。在冷却阶段,由于材料的弹性模量逐渐增大,同时屈服强度也在随温度降低而增加,3个计算案例中A点的纵向残余应力也在随冷却时间增加而增加,且Case B 与Case C的增加速率相当,而Case D的增加速率最慢。热处理完成后,Case B中A点的纵向残余应力最大(约为250 MPa),而Case C与Case D的纵向残余应力明显小于Case B。
图10 热处理过程中A点纵向残余应力随时间的变化
Fig.10 Longitudinal residual stress of point A (in Fig.1a) during heat treatment
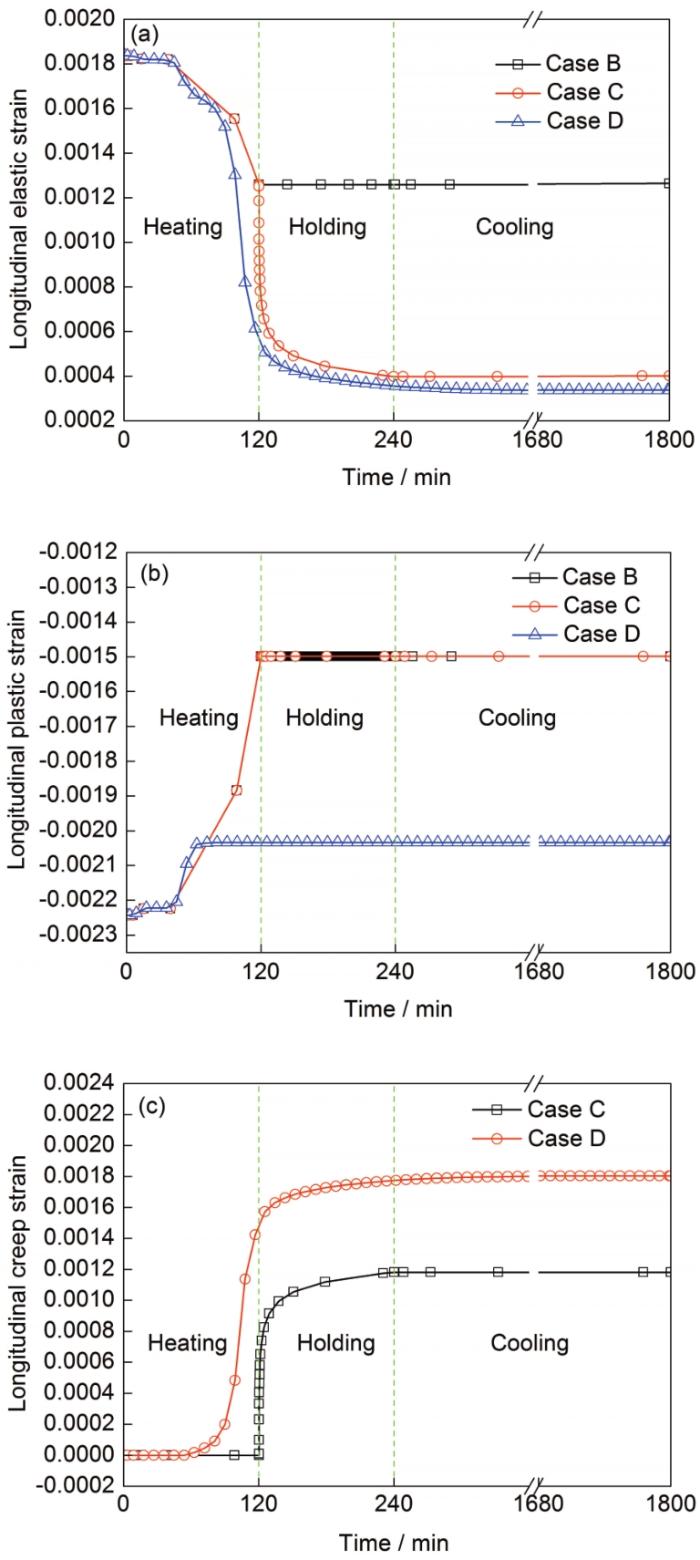
为了探讨3个不同计算案例在热处理过程中的应力随时间变化不同差异的原因,分别从计算结果中提取了A点的纵向弹性应变、塑性应变和蠕变应变随时间的变化曲线,如图11所示。由图分析可知,在热处理的加热阶段,Case B和Case C的纵向弹性应变一直在减小,而压缩塑性应变一直在增加,这是因为随着温度的升高,材料的屈服强度和弹性模量逐渐变小,且屈服强度的降低速率大于弹性模量的降低速率(见图4)。应力是由弹性应变和弹性模量决定的,由式(9)可知,在升温过程中,由于屈服强度的降低速率大于弹性模量的降低速率,促使式(9)右边的值大于左边的值,而这不能满足应力应变的平衡条件,故此时A点的弹性应变只有减小才能满足平衡条件;在不考虑加热过程中蠕变效应的情况下,这部分减小的弹性应变要转化为塑性应变,从而导致A点的纵向应力减小,同时塑性应变增加(图11b)。对于Case D而言,除了上述的材料软化效应导致弹性应变降低外,在加热过程中A点的蠕变应变也一直在增大,A点弹性应变降低速率将会增大,由于蠕变应变的增加使转化为塑性应变的量更少,因此与Case B和Case C相比,Case D的塑性应变量增加较少,而弹性应变减小量比Case B和Case C更大,故加热完成后Case D导致的应力释放更充分。
图11 热处理过程中A点的弹性应变、塑性应变和蠕变应变随时间的变化
Fig.11 Varieties of elastic strain (a), plastic strain (b) and creep strain (c) with time at point A (in Fig.1a) during heat treatment
在保温阶段,Case B的弹性应变、塑性应变都保持不变,这是因为Case B未考虑蠕变效应,在保温阶段材料的屈服强度和弹性模量都保持不变,由式(9)和(10)可知,此时弹性应变和塑性应度都保持不变,故Case B在保温阶段的应力不会变化。对于Case C和Case D而言,它们在保温阶段的弹性应变一直在减小,塑性应变保持不变,而蠕变应变一直在增加。由式(10)可知,此时弹性应变减小的部分将全部转化为蠕变应变。同时在保温阶段,Case C弹性应变的减小量大于Case D,即此阶段Case C的应力释放量大于Case D (图10),这主要是因为在保温阶段刚开始时,Case C中A点的纵向应力大于Case D,由式(5)可知,应力越大,产生蠕变的驱动力也就越大。
在冷却阶段,Case B和Case C的弹性应变、塑性应变都保持不变,随着温度的降低,材料屈服强度的增加速率大于弹性模量的增加速率,因此弹性应变不会转化为塑性应变,但是由于弹性模量随温度降低而升高,导致A点的应力值相应增大。由于Case B在保温阶段的弹性应变大于Case C,所以在冷却过程中,Case B的应力增幅也相应更大。在Case D中,弹性应变在降温过程中略有减小,这是因为降温过程中材料发生了蠕变,由于在热处理加热和保温阶段A点的应力已经得到了极大的释放,故此时蠕变效应相对较弱。
综上所述,由于Case B应力的释放只是由于材料的高温软化导致应力松弛,故最终Case B的应力计算结果高于实验值。由于Case C和Case D除了材料的高温软化导致的应力松弛外,还有蠕变效应导致的应力释放,且蠕变效应相比于材料高温软化对降低弹性应变的贡献更大,故Case C和Case D最终导致的应力释放程度明显大于Case B。Case C虽然只考虑了保温阶段的蠕变,但由于保温阶段Case C的初始应力值大于Case D,这样导致Case C保温阶段产生的蠕变应变大于Case D,最终导致Case C和Case D的应力释放效果基本一致。
(1) 无论是对于焊接残余应力还是热处理后的残余应力,基于本工作所开发的热-弹-塑性有限元方法得到的残余应力结果与实验结果都吻合良好。
(2) Q345钢平板TIG重熔接头经过600 ℃、2 h热处理后,焊接残余应力可以得到较充分的消除,纵向残余应力的峰值降低81%左右,横向残余应力的峰值降低70%左右。
(3) 从数值模拟结果可知,在焊后热处理过程中“蠕变效应”比“材料软化效应”对消除残余应力的贡献更大。在不考虑材料的高温蠕变时,热处理后预测的纵向残余应力峰值与热处理前相比降低了32%左右,横向残余应力峰值下降了18%左右。
(4) 只考虑保温阶段蠕变效应的材料模型与考虑整个热处理过程蠕变效应的材料模型相比,在不损失计算精度的前提下可使计算效率提高10倍左右。
(5) 热处理过程消除残余应力,是加热过程中材料屈服强度的减小速率大于弹性模量的减小速率,从而导致的弹性应变降低和蠕变效应导致应力松弛共同作用的结果。
1 实验方法
1.1 单道重熔试件制作
图1
1.2 焊后热处理实验
图2

1.3 残余应力测量
图3

2 数值模拟方法
图4

2.1 有限元模型
图5
2.2 热源模型
2.3 应力场计算
2.4 焊后热处理
2.5 计算案例

3 结果比较与讨论
3.1 残余应力比较
图6

图7

图8
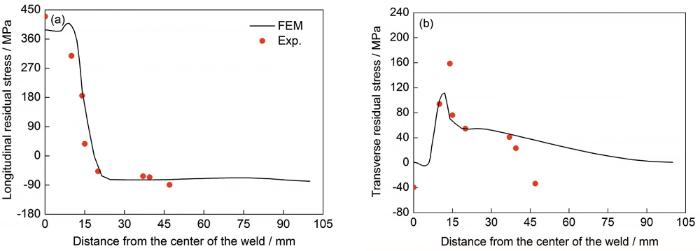
图9

3.2 计算效率比较
3.3 热处理消除残余应力的机理探讨
图10
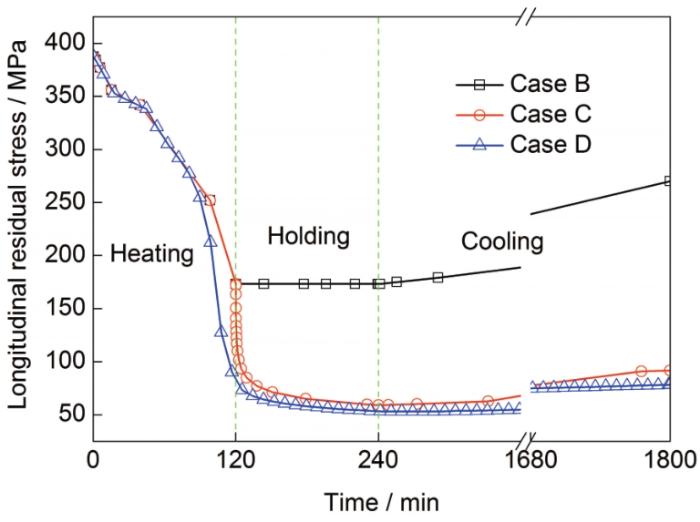
图11
4 结论
来源--金属学报







 沪公网安备31011202020290号
沪公网安备31011202020290号
