分享:第一性原理研究反位缺陷对TiAl基合金力学行为的影响
采用第一性原理计算方法,计算了二元γ-TiAl基合金的广义层错能(GSFE)随成分的变化,获得了TiAl基合金中孪晶(TW)、普通位错(OD)、超晶格位错(SDI和SDII)等变形模式的形变势垒,分析了在外加应力作用下的变形模式选择,并讨论反位缺陷对二元γ-TiAl基合金塑性的影响。计算结果表明,TiAl反位缺陷能降低以超晶格内禀层错(SISF)为前缘分位错的TW变形模式的势垒,且扩大TW模式开动的剪切应力角度窗口,有利于改善TiAl基合金的塑性。AlTi反位缺陷则反之。AlTi反位缺陷降低了以复杂层错(CSF)为前缘分位错的OD和SDII变形模式的滑移势垒(γEB),而且扩大了它们开动的剪切应力角度窗口,可促进OD和SDII的滑移。由于CSF的滑移势垒比SISF高,因此,相较于以SISF为前缘分位错的TW变形模式,OD及SDII滑移对应的强度较高、塑性较差。计算结果较好地说明了AlTi反位缺陷对TiAl基合金塑性的改善没有TiAl反位缺陷明显的原因。
关键词:
TiAl基合金具有高比强度以及良好的氧化和蠕变抗力,是一种性能优越的高温结构材料,可用来制备航空发动机及燃气涡轮机中的高温部件[1,2,3]。然而TiAl基合金尤其是具有四方L10结构的γ-TiAl合金的低温塑性仅为2%~3%[4],使其机械加工困难,极大地限制了TiAl基合金在工业领域中的应用[4,5,6]。
合金化是提高合金性能的有效途径。非标准化学剂量比TiAl基合金中,过量Ti或Al以反位缺陷TiAl或AlTi形式存在,亦可被看作特殊的合金化元素。因此,TiAl基合金中Ti、Al相对含量对力学性能的影响受到了广泛关注。Tsujimoto等[7]采用压缩实验测试了非标准化学剂量比TiAl基合金的塑性,发现TiAl基合金的塑性与其Al含量密切相关,即富Al合金表现为脆性,而富Ti合金脆性有所改善。Hall等[8]通过对比Ti48Al52和Ti52Al48合金的室温变形行为,也发现Ti52Al48合金的塑性优于Ti48Al52合金。然而,在富Ti合金中,并非Al含量越低(或Ti含量越高)塑性越好。Huang等[9]研究了室温下二元TiAl基合金的力学行为随Al含量(46%~60%,原子分数,下同)的变化关系,发现Al含量在46%~50%时,二元TiAl基合金的塑性比较好,尤其是当Al含量为48%~50%时,塑性最高。Darolia等[10]对Ti-xAl-2Cr-2Nb (原子分数,%)合金的研究结果表明,Ti-48Al-2Cr-2Nb (原子分数,%)合金的塑性最高,Al含量为45%或者更低时,合金的塑性很低或者没有塑性。研究[11]发现,Ti-44.5Al二元合金的塑性拉伸率仅为1.4%。由此可见,Al含量或者说反位缺陷对TiAl基合金力学行为的影响较为复杂,仍然需要进一步研究。
材料的力学性质与其变形模式密切相关。本文作者的前期工作[12]采用第一原理方法计算了TiAl基合金不同变形模式下的广义层错能(generalized stacking fault energy,GSFE),分析了不同加载方向下各变形模式对应的有效滑移势垒,较好地解释了γ-TiAl在外加应力下的变形模式选择行为。为了深入理解非化学剂量比TiAl基合金中反位缺陷对γ-TiAl力学性能的影响,本工作采用第一原理方法计算了不同化学剂量比TiAl基合金中不同变形模式对应的广义层错能及变形势垒,分析了反位缺陷对外加载荷下γ-TiAl变形模式选择的影响。
广义层错能[13,14]描述了剪切变形过程中一半晶体沿某一原子面上的特定方向相对另一半晶体发生相对滑移时系统的能量变化,目前,已被成功用于研究晶体中的位错性质[15,16]和变形模式[17,18,19]等问题。广义层错能(γGSFE)可计算如下[20]:
式中,E0为未滑移完整晶体的能量,E(x, y)为一半晶体相对另一半晶体沿某一滑移面上特定方向滑移(x, y)位移时晶体的能量,S是发生切变的面积。
四方L10结构的γ-TiAl的密排面为(111)面,是γ-TiAl变形过程中的主滑移面[21]。因此,本工作考虑(111)面上不同滑移方向对应的GSFE。γ-TiAl的主要变形模式有3种,分别为孪晶(twinning,TW)、普通位错(ordinary dislocation,OD)和超晶格位错(superlattice dislocation,SD)。3种变形模式对应的Burgers矢量分别为
图1 L10结构TiAl (111)面滑移/孪晶变形模式示意图
Fig.1 Schematic for the slip/twinning systems on (111) plane of L10-TiAl, together with Burgers vectors for superlattice dislocation (SD, [10
Color online
由不同滑移路径上GSFE的变化,可以获得γ-TiAl合金的各类稳定层错能(γSF),如超晶格内禀层错(γSISF)、复杂层错能(γCSF)、孪晶能(γTW)、反相畴界能(γAPB)等及相应的非稳定层错能(γUSF),如非稳定内禀层错能(γUSISF)、非稳定复杂层错能(γUCSF)、非稳定孪晶能(γUTW)和非稳定反相畴界能(γUAPB)。稳定层错能与非稳定层错能的差决定了相应路径的滑移势垒(slip energy barrier,γEB),即γEB = γUSF-γSF。
本工作采用基于密度泛函理论(density functional theory,DFT)[28]的精确muffin-tin轨道(exact muffin-tin orbitals,EMTO)方法[29,30,31,32]进行总能计算。选用Perderw、Burke和Ernzerhof (PBE)参数化的广义梯度近似(generalized gradient approximation,GGA)[33]处理交换关联泛函。电子自洽计算过程中,采用标量相对近似,在软核模式下求解单电子方程。波函数基组包含s、p和d成分。Ti及Al原子的价电子构型设置为Ti-3d24s2和Al-3s23p1。经过收敛性测试,k点网格选为13×7×3。
作为对照,采用VASP[34,35,36]软件包中的全电子投影缀加波法(projector augmented-wave)[37]对标准化学剂量比TiAl进行了计算。交换关联泛函采用与EMTO计算相同的PBE广义梯度近似。平面波截断能设定为400.0 eV。Brillouin区k点的取样采用Monkhorst-Pack方法,且取样间距低于2π×0.3 nm-1。采用共轭梯度法(conjugate gradient,CG)进行晶体结构优化。每一自洽循环能量差低于1.0×10-6 eV;每个原子上的作用力小于0.01 eV/nm作为收敛判据。
经过层错能收敛性测试,最终采用由6个(111)面原子层组成的超晶胞结构模型(共12个原子)计算γ-TiAl的GSFE。该超晶胞结构的3个晶格矢量a、b和c分别为
式中,
如上所述,a、b和c为超晶胞结构的晶格矢量模。若a0为γ-TiAl的单胞晶格常数,则a、b和c分别为
在计算中,考虑了标准化学剂量比TiAl,富Ti合金Ti(Al1-mTim),富Al合金(Ti1-mAlm)Al。富Ti及富Al合金中,过量Ti及Al分别以TiAl及AlTi反位缺陷形式存在,其浓度m变化范围为0.0~10.0%,间隔2.5%。在EMTO计算中,反位缺陷在晶格上的相应子晶格上的无序分布采用相干势(coherent-potential approximation,CPA)描述。
首先以标准化学剂量比TiAl、富Ti合金Ti(Al0.9Ti0.1)、富Al合金(Ti0.9Al0.1)Al为例,考察GSFE沿不同滑移路径的变化。
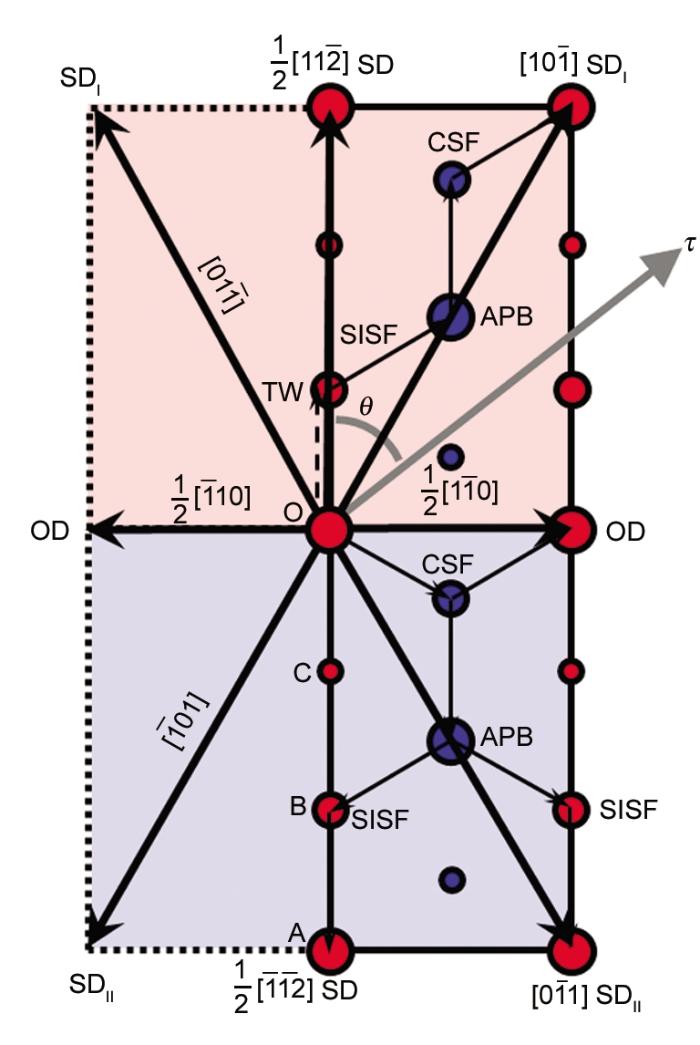
图2给出了(111)滑移面内以SISF为前缘分位错的变形过程中的GSFE随位移的变化曲线。由图可见,在TW滑移路径上,存在2个滑移势垒,分别为γUSISF及γUTW,其中γUTW略高于γUSISF。二者之间的GSFE谷点为γSISF。在此滑移路径上,富Ti合金的GSFE显著低于标准化学剂量比TiAl,即,TiAl反位缺陷能够促进TW变形。富Al合金的GSFE仅略低于标准化学剂量比TiAl,说明AlTi反位缺陷对孪晶变形的影响较小。
图2 TiAl、Ti(Al0.9Ti0.1)和(Ti0.9Al0.1)Al合金中以超晶格内禀层错(SISF)为前缘分位错的变形模式(TW和SDI)对应的广义层错能曲线
Fig.2 Generalized stacking fault energies (γGSFE) for the SISF partial dislocation leading deformation models (TW and SDI) of TiAl, Ti(Al0.9Ti0.1) and (Ti0.9Al0.1)Al alloys (γSISF and γUSISF, γCSF and γUCSF, γTW and γUTW, γAPB and γUAPB stand for the stable and unstable stacking fault energy for SISF, CSF, TW, and APB, respectively)
Color online
在SDI滑移路径上,存在3个滑移势垒,分别为γUSISF、γUAPB以及γUCSF。其中γUAPB最高,γUCSF次之,γUSISF最低。在γUAPB及γUCSF之间存在γAPB及γCSF。富Ti合金中的TiAl反位缺陷及富Al合金中的AlTi反位缺陷均降低前缘分位错SISF之后的GSFE,其中,TiAl反位缺陷的作用更为明显。
图3给出了(111)滑移面内以CSF为前缘分位错的变形过程中GSFE随位移的变化曲线。由图可见,在OD滑移路径上,存在2个滑移势垒,即2个γUCSF。二者之间的GSFE谷点为γCSF。该滑移路径上,富Ti合金及富Al合金的GSFE均低于标准化学计量比TiAl,其中TiAl反位缺陷的作用显著。
图3 TiAl、Ti(Al0.9Ti0.1)和(Ti0.9Al0.1)Al合金中以复杂层错(CSF)为前缘分位错的变形模式(OD和SDII)对应的广义层错能曲线
Fig.3 γGSFE for the CSF partial dislocation leading deformation models (OD and SDII) of TiAl, Ti(Al0.9Ti0.1) and (Ti0.9Al0.1)Al alloys
Color online
在SDII滑移路径上,存在3个滑移势垒,分别为γUCSF、γUAPB及γUSISF,且γUAPB>γUCSF>γUSISF。在γUCSF及γUAPB之间存在稳定γCSF及γAPB。γSISF存在于γUAPB及γUSISF之间。TiAl反位缺陷和AlTi反位缺陷均降低了此滑移路径上的GSFE,且前者作用效果较明显。
由计算得到的GSFE随滑移路径的变化,可以获得γ-TiAl的稳定层错能(γSISF、γCSF、γTW、γAPB)和非稳定层错能(γUSISF、γUCSF、γUAPB)。
本工作采用EMTO-CPA方法计算非化学剂量比TiAl基合金的GSFE,因此难以考虑反位缺陷及层错引起的局域晶格弛豫。为评估局域晶格弛豫对GSFE的影响,作为比较,采用第一原理平面波赝势方法VASP[34,35,36]对标准化学剂量比TiAl的稳定层错能及非稳定层错能进行了计算,见表1。可见,采用EMTO方法计算得到的稳定和非稳定层错能与未进行晶格弛豫的VASP计算结果吻合较好,误差均在5%以下。比较EMTO及未晶格弛豫VASP计算结果与经晶格弛豫的VASP计算结果[12,39],三者稳定层错能仍然符合良好,但未晶格弛豫计算结果显著高于晶格弛豫后的计算结果,即晶格弛豫效应对非稳定层错能的影响较为显著。然而,晶格弛豫对非稳定层错能的相对大小(γUAPB>γUCSF>γUSISF)没有影响。此外,值得注意的是,文献[39]采用轴比为1.023的计算模型,对比层错能结果表明轴比为1引起的层错能误差可忽略,与本文作者前期工作的结果[12]类似。因此,未晶格弛豫计算结果仍可用来判断各变形机制的难易程度。另外,EMTO计算和其它理论结果[12,39,40,41]中的稳定层错能,都符合如下顺序:γAPB>γCSF>γSISF (表1)。
表1 标准化学计量比γ-TiAl的稳定层错能及非稳定层错能
Table 1
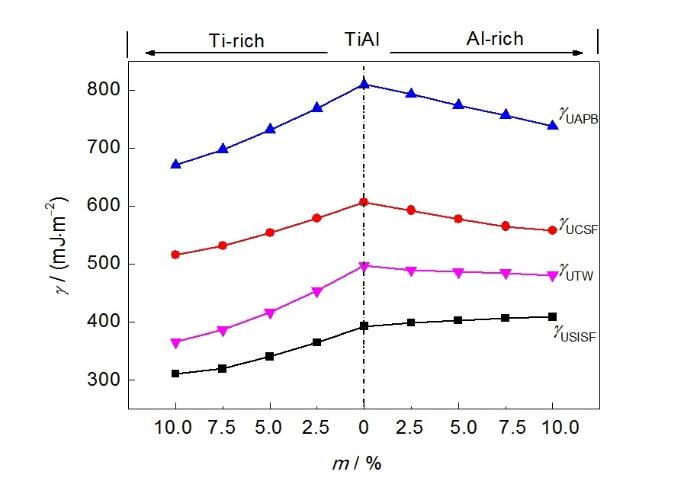
图4给出了稳定层错能随非化学剂量比TiAl成分的变化。可见,稳定层错能随反位缺陷浓度的增加而降低,随TiAl反位缺陷浓度增加而降低的幅度大于随AlTi反位缺陷浓度增加而降低的幅度。Woodward等[41]用LKKR-CPA方法计算了γSISF及γAPB,其随成分的变化趋势与本工作结果一致,但γSISF低于本工作计算结果。Zhang等[42]用透射电子显微镜(TEM)方法测量了Ti-49.6Al、Ti-48.0Al,Hug等[22]和Stucke等[43]用弱束透射电子显微镜(WB-TEM)方法测得Ti-54.0Al和Ti-56.0Al的γSISF,其结果分别为98、67、140和116 mJ/m2,低于本工作计算结果,但其随反位缺陷浓度变化的趋势与实验报道结果一致。计算得到的γAPB也显著高于实验测量结果[22,41]。需要强调的是,实验测量结果往往受到TEM技术分辨率的限制,其精度较低,从而影响测量结果。
图4 Ti(Al1-mTim)和(Ti1-mAlm)Al合金的稳定层错能随反位缺陷浓度(m)的变化
Fig.4 Calculated γSISF (a), γCSF (b), γAPB (c) and γTW (d) of Ti(Al1-mTim) and (Ti1-mAlm)Al against concentration of antisite defects (m) (The Ti-rich and Al-rich cases are separated with the vertical dashed line at zero)
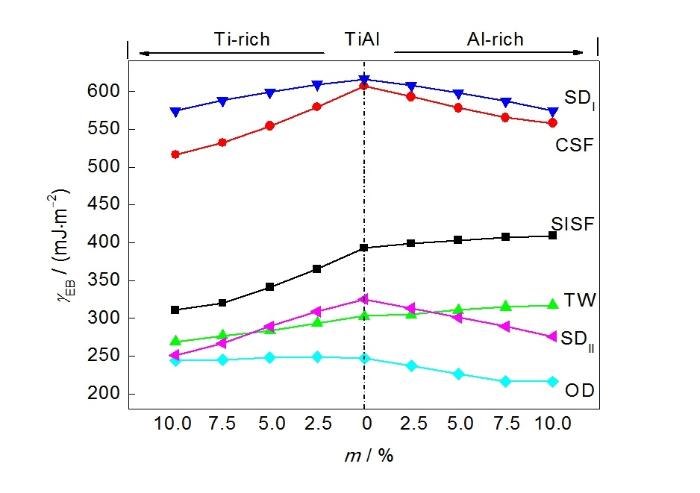
图5给出了γUSISF、γUCSF、γUAPB和γUTW随反位缺陷浓度的变化曲线。可见,对于富Ti合金,4种非稳定层错能均随着反位缺陷TiAl浓度的升高而降低,说明富Ti合金中的TiAl反位缺陷有助于降低γ-TiAl中的位错滑移势垒,提高其塑性变形能力。对于富Al合金,与富Ti合金类似,γUCSF、γUAPB和γUTW随AlTi反位缺陷浓度增加而降低,但降低的幅度小于其随TiAl反位缺陷浓度的变化。值得注意的是,γUSISF随AlTi反位缺陷浓度的增加而升高,且γUCSF和γUAPB相对于γUTW降低更为明显,说明富Al合金中反位缺陷AlTi可以促进前缘分位错CSF、SD和TW的形成,而对另一种前缘分位错SISF的激发形成一定的阻碍。
图5 Ti(Al1-mTim)及(Ti1-mAlm)Al合金的γUSISF、γUCSF、γUAPB和γUTW 随m的变化
Fig.5 Calculated γUSISF, γUCSF, γUAPB and γUTW of Ti(Al1-mTim) and (Ti1-mAlm)Al against m (The Ti-rich and Al-rich cases are separated with the vertical dashed line at zero)
Color online
由图2和3可知,在γ-TiAl中的变形路径可进行分解,即其位错滑移由一系列分位错滑移组成。每一分位错滑移均对应一个滑移势垒,其中最高的势垒决定了该变形的难易程度。不同变形模式的滑移势垒由其变形过程中各滑移路径所对应的滑移势垒的最大值决定。据此,TW、SDI、OD和SDII的滑移势垒分别为γUTW-γSISF、γUAPB-γSISF、γUCSF-γCSF和γAPB-γCSF。2种前缘分位错SISF及CSF的滑移势垒分别为γUSISF和γUCSF。
图6给出了前缘分位错及各变形模式滑移势垒随反位缺陷浓度的变化。可见,反位缺陷TiAl可降低前缘分位错SISF的滑移势垒,而反位缺陷AlTi却使SISF的滑移势垒略微升高,表明富Ti合金相对于标准化学计量比和富Al合金中的前缘分位错SISF更容易滑移。2种反位缺陷均降低CSF的滑移势垒,且反位缺陷TiAl的作用效果更为明显。TW的滑移势垒随反位缺陷TiAl浓度的升高而降低,但随AlTi含量的增加而升高,表明富Ti合金有利于TW变形,而富Al合金中TW变形受到阻碍。SDI的滑移势垒随2种反位缺陷浓度升高均降低,且下降幅度基本相同,说明TiAl及AlTi反位缺陷对TiAl中的SDI变形难易程度的影响基本相同。由于SDI的滑移势垒相对较高,通常较难开动,因此,在实验中也很难观察到。富Ti合金中,OD的滑移势垒不随反位缺陷TiAl含量的变化而改变。富Al合金中,OD的滑移势垒随反位缺陷AlTi浓度的升高而降低,表明富Al合金中OD变形模式相对更容易开动。SDII的滑移势垒随2种反位缺陷含量的增加而降低,且富Ti合金SDII的滑移势垒降低略显著。
图6 γ-TiAl合金中不同变形模式对应的滑移势垒(γEB)随m的变化曲线
Fig.6 Slip energy barrier (γEB) of various deformation modes in γ-TiAl alloys as a function of m (The Ti-rich and Al-rich cases are separated with the vertical dashed line at zero)
Color online
γ-TiAl的变形过程中,变形模式的选择不仅取决于相应位错的γEB,而且与外加应力的加载方向密切相关。加载方向与滑移方向的夹角决定了作用在该滑移系上的分切应力大小。对于相同的外加应力,作用在某一滑移系上的分切应力越小,则该滑移系越难启动,换而言之,该滑移系的有效滑移势垒越高。
设作用在滑移面(111)上的外加切应力与滑移面内孪晶方向[11
结合前文滑移势垒的分析及图1,变形模式TW和SDI、OD和SDII对应的有效滑移势垒为:
由图6可知,各变形模式对应的滑移势垒随反位缺陷浓度的变化单调变化,因此,选取标准化学剂量比TiAl、Ti(Al0.9Ti0.1)和(Ti0.9Al0.1)Al合金讨论反位缺陷浓度对有效滑移势垒的影响。
图7给出了标准化学计量比γ-TiAl、Ti(Al0.9Ti0.1)和(Ti0.9Al0.1)Al的前缘分位错SISF和CSF的有效滑移势垒随θ的变化。可见,在低θ角度范围内时,SISF分位错的有效滑移势垒低于CSF,即,在此方向外加应力作用下,SISF前缘分位错开动,CSF分位错受到抑制。SISF分位错有效滑移势垒随θ增加而增加,即变形难度增加,强度增加。高θ角时,CSF前缘分位错开动,SISF分位错受到抑制。在θ为120°左右时,CSF分位错有效滑移势垒最低,最易开动。
图7 前缘分位错SISF和CSF的有效滑移势垒(
Fig.7 Effective slip energy barriers (
Color online
对于标准化学剂量比TiAl,由SISF前缘分位错开动向CSF开动转变的临界角度为67°。反位缺陷TiAl将临界角度增加为68°,SISF前缘分位错开动的角度范围略增大,相应地,CSF前缘分位错的开动角度范围略减小。反位缺陷AlTi使临界角度减小为65°,因此,前缘分位错CSF激发角度范围增大,SISF分位错激发角度范围相应减小。因此,反位缺陷TiAl有利于前缘分位错SISF的滑移,而反位缺陷AlTi则促进前缘分位错CSF的滑移。
图8给出了以SISF为前缘分位错的TW及SDI变形模式的有效滑移势垒随θ的变化。图8中,θ角仅考虑到67°左右,即,SISF前缘分位错开动向CSF转变的临界角度。超出此角度范围,CSF前缘位错启动,后续变形不再是TW和SDI模式。可见,在低θ角度范围内,TW变形模式的有效滑移势垒低于SDI,即TW变形模式开动,SDI受到抑制。随θ增加,TW有效滑移势垒增加。在很窄的高角度范围内,SDI的有效滑移势垒低于TW,SDI变形模式开动,TW受到抑制。与低角度的TW变形模式相比,SDI变形模式的有效滑移势垒较高。
图8 以SISF为前缘分位错的变形模式TW和SDI的
Fig.8
Color online
对于标准化学剂量比TiAl,TW变形模式向SDI转变的临界角度为61°,即TW变形模式开动的剪切应力角度窗口为0°~ 61°,SDI开动的剪切应力角度窗口为61°~67°。富Ti合金Ti(Al0.9Ti0.1)的TW变形模式开动的角度窗口为0°~63°,略窄于标准化学剂量比TiAl;SDI变形模式的角度窗口为63°~68°。对于富Al合金(Ti0.9Al0.1)Al,TW变形模式的角度窗口为0°~57°,SDI的角度窗口为57°~65°。由此可见,TiAl反位缺陷对TW及SDI变形模式开动的剪切应力角度窗口影响较小,但AlTi反位缺陷显著减小TW变形模式角度窗口,增大SDI角度窗口。
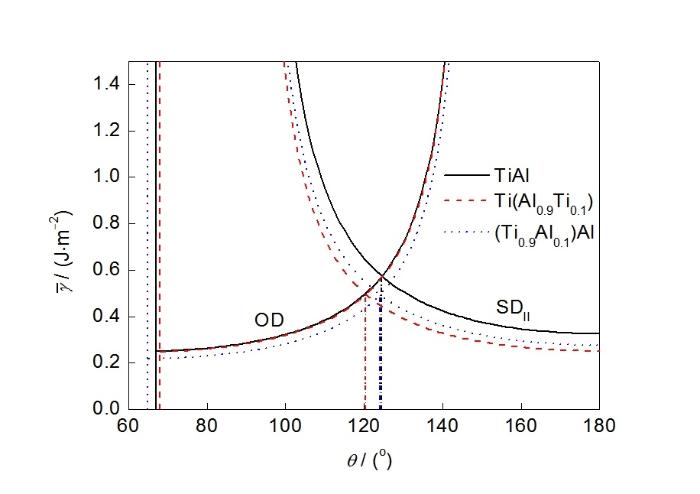
图9给出了以CSF为前缘分位错的OD及SDII变形模式的有效滑移势垒随θ的变化。图9中,θ始于CSF前缘分位错开动的临界角度67°左右。可见,在较低的角度范围内,OD的有效滑移势垒低于SDII,OD变形模式开动,其有效滑移势垒随θ增加而增加。在高角度范围内,SDII的有效滑移势垒低于OD,SDII变形模式开动,其有效滑移势垒随θ增加而减小。
图9 以CSF为前缘分位错的变形模式OD和SDII的
Fig.9
Color online
对于标准化学剂量比TiAl,OD变形模式开动的外加剪切应力的角度窗口为67°~125°,SDII的角度窗口为125°~180°。富Ti合金Ti(Al0.9Ti0.1)的OD变形模式的角度窗口收窄,为68°~120°,SDII的角度窗口扩大为120°~180°。富Al合金(Ti0.9Al0.1)Al OD变形模式的角度窗口为65°~125°,宽于标准化学剂量比TiAl,SDII的角度窗口基本不变。
由第2节计算结果可知,富Ti合金中,TiAl反位缺陷降低了以SISF为前缘分位错的TW变形模式的滑移势垒,且扩大了TW变形模式开启的剪切应力角度窗口。因此,TiAl反位缺陷有利于TiAl基合金中形变孪晶的形成,从而改善TiAl合金的塑性。富Al合金中,虽然TW的稳定和非稳定广义层错能均随AlTi含量的增加而降低,但其滑移势垒却呈现出相反的变化趋势,说明富Al合金中TW变形模式受到阻碍。另外,TW的有效滑移势垒略微升高,同时其可激发角度范围缩小,使得TW的开启可能性降低。因此,从孪晶变形模式来说,AlTi反位缺陷不利于提高TiAl合金的塑性。同样以SISF为前缘分位错的SDI变形模式开启的角度窗口较窄,且有效滑移势垒较高,因此在实验中较难观察到。上述结果与Hall等[8]的实验观察结果符合较好。他们发现,Ti52Al48合金样品在变形后,在γ-TiAl基体中存在高密度的形变孪晶,但Ti48Al52 形变孪晶密度较低。力学性能测试结果表明,Ti52Al48的塑性高于Ti48Al52。
富Al合金中,反位缺陷AlTi的出现降低了OD和SDII变形模式的有效滑移势垒,且扩大了它们的可激发角度范围。因此,AlTi反位缺陷有利于OD和SDII的滑移。Hall等[8]对Ti48Al52合金的观察表明,其主要的变形模式是
如上所述,本工作结果较好地说明了TiAl反位缺陷能比AlTi反位缺陷更好地提高γ-TiAl的塑性的原因,但仍不能说明为什么在Al含量低于46% (即TiAl反位缺陷超过4%)时,γ-TiAl的塑性反而降低。文献[8]认为,这可能与成分引起的微观组织变化有关。Al含量低于46%时,TiAl基合金具有γ+α2的全片层组织,具有较大的晶粒尺寸,直径为200~500 μm,使其塑性低于Al含量为48% ~50%的双态组织。
(1) γ-TiAl合金的非稳定超晶格内禀层错能随AlTi反位缺陷浓度增加而增加外,稳定及非稳定层错能随2种反位缺陷浓度的增加均降低,且TiAl反位缺陷作用效果更显著。
(2) 富Ti合金中,SISF和CSF前缘分位错以及γ-TiAl (111)滑移面内变形模式TW、SDI和SDII的滑移势垒随TiAl反位缺陷浓度的增加而降低,但OD的滑移势垒不受TiAl反位缺陷浓度的影响。富Al合金中,SISF前缘分位错和TW变形模式随AlTi反位缺陷浓度增加而增加,而CSF前缘分位错和其余变形模式的滑移势垒均随AlTi反位缺陷浓度的变化趋势相反。
(3) TiAl反位缺陷扩大了SISF前缘分位错以及变形模式TW和SDII的外加应力角度窗口,CSF前缘分位错以及变形模式SDI、OD和SDII的外加应力角度窗口随AlTi反位缺陷浓度的增加而增大。
1 计算方法和参数设置
图1
2 结果与讨论
2.1 广义层错能随位移的变化
图2
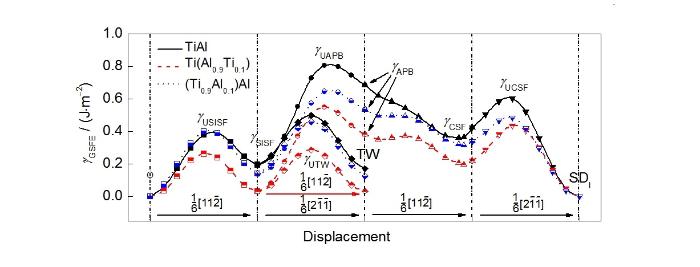
图3
2.2 稳定层错能及非稳定层错能
Method
γSISF
γUSISF
γCSF
γUCSF
γTW
γUTW
γAPB
γUAPB
EMTO
194
393
360
607
170
497
685
810
VASP unrelaxed
189
375
363
590
179
475
684
787
VASP relaxed[12]
181
316
358
560
177
410
657
735
VASP relaxed[39]
184
321
355
522
182
409
FLAPW[40]
172
363
667
LKKR[41]
123
294
672
Exp.[22]
~77
~145
图4
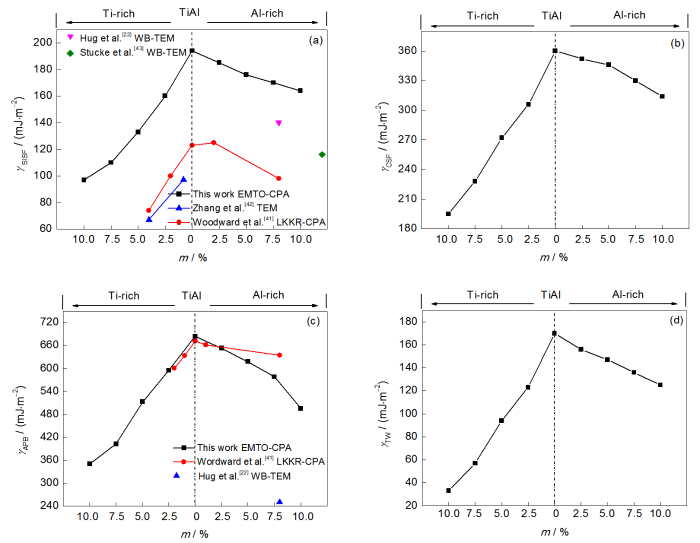
图5
2.3 滑移势垒
图6
2.4 外加载荷下的有效滑移势垒及变形模式选择
图7

图8
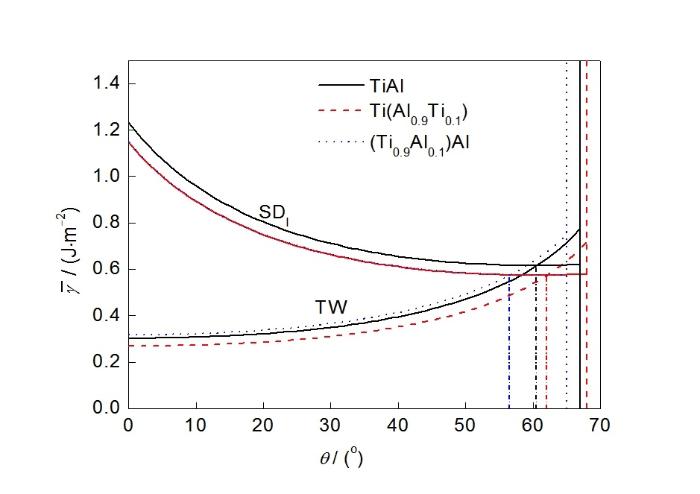
图9
3 分析讨论
4 结论
来源--金属学报







 沪公网安备31011202020290号
沪公网安备31011202020290号
