分享：Ni-Mn-Ga-Ti铁磁形状记忆合金的相稳定性和磁性能的第一性原理计算

白静,1,2,3,4, 石少锋1,2, 王锦龙1,2, 王帅2, 赵骧1

以Ni-Mn-Ga合金为代表的铁磁形状记忆合金是新型的智能材料，具有高达10%的磁诱导应变以及千赫兹级别的响应频率[1,2,3,4,5,6]。这类合金具有优良的物理特性和巨大的开发潜力，可作为驱动器、传感器、磁微机电系统[7]等，从而成为目前国际金属材料和凝聚态物理研究的热点之一。

然而，Ni-Mn-Ga合金固有的高脆性极大地限制了它的实际应用，研究者们致力于通过掺杂第四组元来改善其延展性，目前主要的合金化组元为一些稀土元素[8,9,10]、Fe[11,12]、Co [13,14]、Cu[15,16,17,18,19,20]等。近期的研究[21]表明，在合适的时效处理下，Ti掺杂可以析出适量的Ni3Ti析出物，从而显著提高Ni-Mn-Ga合金的压缩强度和延展性。断口形貌观察表明，晶间断裂和穿晶断裂的混合方式是Ni53Mn23.5Ga18.5Ti5合金力学性能改善的主要原因[22]。Dong等[23]观察到Curie温度(TC)和饱和磁化强度均随Ti含量的增加而降低。Gao等[24]通过第一原理计算，从奥氏体和马氏体之间的总能量差的角度阐明了Ni50Mn25Ga25-yTiy (y为掺杂Ti的原子分数)合金的马氏体相变温度随Ti含量增加而降低的原因。

目前，Ni-Mn-Ga-Ti合金的TC和饱和磁化强度随Ti含量变化的本质原因尚不清楚。因此，本工作的主要目的是通过第一性原理计算研究Ni8Mn4-xGa4Tix (x为单胞中掺杂Ti原子的个数，x=0、0.5、1、1.5和2)合金中Ti掺杂对合金相稳定性、磁性能和电子结构的影响规律和作用机理，旨在解释实验现象和阐明相关机理，力图对实验观察到的掺杂Ti而导致的TC和磁性能的降低给出理论解释及支撑。

1 计算方法

使用量子力学计算软件包Vienna ab-initio software package (VASP)，基于密度泛函理论进行第一性原理计算[25,26]。离子和电子之间的相互作用由投影缀加波(projector-augmented wave，PAW)[27,28]方法描述。选用Perdew和Wang[29]提出的广义梯度近似 (generalized gradient approximation，GGA) 来描述交换相关能。所对应的金属元素的电子构型分别为Ni (3d84s2)、Mn (3d64s1)、Ga (4s24p1)和Ti (3d34s1)。为方便叙述，本工作将Ni8Mn4-xGa4Tix (x=0、0.5、1、1.5和2)合金按照Ti含量分别用X0、X0.5、X1、X1.5和X2表示。k点网孔用Monkhorst-Pack[30]方法产生：对于X0、X1和X2合金，在一个含有16个原子的奥氏体单胞(如图1a所示)中使用8×8×8的k点网格；对于X0.5和X1.5合金，建立一个1×1×2的超胞，故k点网格的选取为8×8×4。

图1

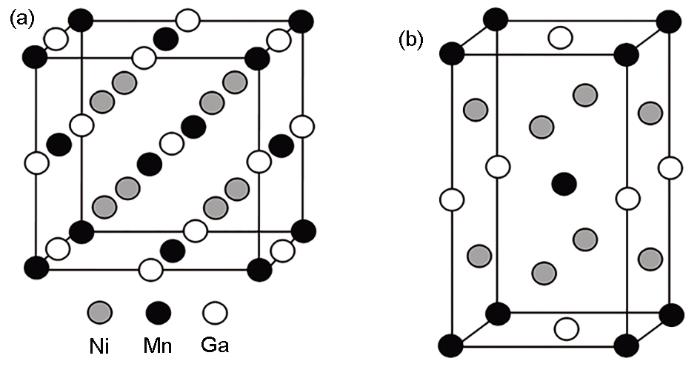
图1   Ni2MnGa合金的晶体结构示意图

Fig.1   Schematics of crystal structures of Ni2MnGa alloy

(a) cubic L21 austenite

(b) tetragonal non-modulated martensite (NM)

在PAW-GGA近似下截断能选取350 eV，并在结构优化时考虑电子自旋极化的影响。另外，在驰豫的过程中单胞内的原子位置和单胞体积也均被优化。VASP程序包计算出的磁结构是线性的(磁矩投影到垂直轴上)。原子磁矩被定义为投影到原子轨道上的自旋密度差。Ni、Mn、Ga和Ti的Wigner-Seitz半径分别为0.1286、0.1323、0.1402和0.1323 nm。在计算中为了得到Ni-Mn-Ga-Ti合金的TC，考虑了奥氏体相的顺磁和铁磁2种磁性状态。

Ni2MnGa合金的立方奥氏体和四方非调制马氏体相(non-modulated martensite，NM)所属的空间群分别为Fm$\overline{3}$m和I4/mmm，对应的晶体结构如图1所示。通常NM是Ni-Mn-Ga合金的热力学最稳定相，是马氏体转变过程的最终产物[31]。

为了研究Ti掺杂对合金相稳定性和TC的影响，计算了Ni8Mn4-xGa4Tix (x=0、0.5、1、1.5和2)合金顺磁奥氏体(PA)和铁磁奥氏体(FA)的形成能(Eform)[32,33]：

式中，Etot (Ni8Mn4-xGa4Tix)是Ni8Mn4-xGa4Tix (x=0、0.5、1、1.5和2)单胞的基态总能量; E0Ni、E0Mn、E0Ga和E0Ti分别是纯Ni、Mn、Ga和Ti在其参考状态下每个原子的基态总能量。

2 结果与讨论

2.1 优先占位和结构优化

为了建立正确的Ni-Mn-Ga-Ti四元合金的晶体结构模型，首先研究了掺杂的Ti元素在Ni2MnGa里的优先占位情况。通常用Eform来表征固态物质的相稳定性[34]。形成能被定义为化合物的基态总能量减去相关纯元素在参考态下的总能量，并将结果归一化[34]。掺杂的Ti原子在Ni2MnGa单胞中有3个可能的占位：Ni位、Mn位或Ga位，见图1a，所对应的Eform分别为-242.43、-324.30和-234.27 meV/atom。低的Eform意味着系统可以更稳定地存在，即优先占位。因此，Ti原子倾向于占据Ni2MnGa合金中的Mn位。

确定了Ti在 Ni2MnGa合金中的优先占位之后，系统地计算了Ni8Mn4-xGa4Tix (x=0、0.5、1、1.5和2)合金的FA和NM的平衡晶格常数，结果列于表1中。可以看出，对Ni2MnGa的计算结果与文献[35,36]报道的实验值吻合得很好。从表1可以看出，随着Ti含量的增加，FA相的晶格常数逐渐增大，这主要是由于Ti的原子半径(0.2 nm)大于所取代的Mn的原子半径(0.179 nm)所致。而对于NM相，晶格常数a增加，c减小，导致晶格四方度c/a比降低。

表1   Ni8Mn4-xGa4Tix (x=0、0.5、1、1.5和2)合金的铁磁奥氏体(FA)和非调制马氏体相(NM)的平衡晶格参数

Table 1  Equilibrium lattice parameters (a and c) of the ferromagnetic austenite (FA) and NM phases of Ni8Mn4-xGa4Tix (x=0, 0.5, 1, 1.5 and 2) alloys

新窗口打开| 下载CSV

2.2 相稳定性和Curie温度

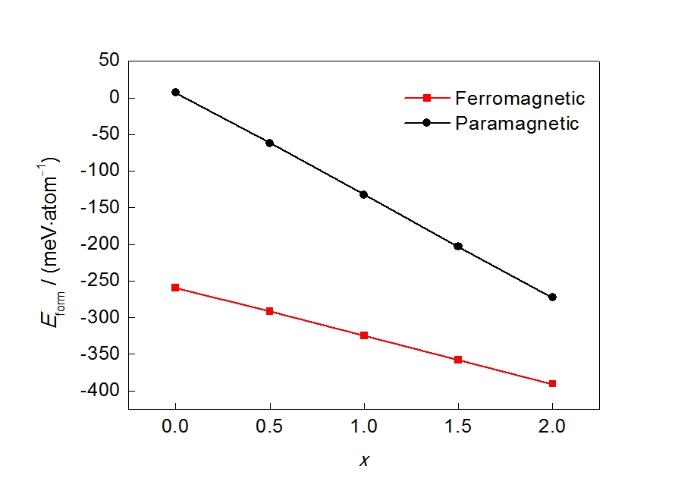
通过计算得到Ni8Mn4-xGa4Tix (x=0、0.5、1、1.5和2)合金的顺磁和铁磁奥氏体相的形成能随Ti含量的变化，并将结果示于图2。从图2可以看出，顺磁奥氏体的Eform远高于铁磁奥氏体，这与顺磁奥氏体是高温相的事实相一致。顺磁和铁磁奥氏体两相之间的临界温度即TC。当Ti含量逐渐增加时，无论是顺磁奥氏体还是铁磁奥氏体，其形成能均逐渐降低，表明稳定性均有所提高。

图2

图2   Ni8Mn4-xGa4Tix (x=0、0.5、1、1.5和2)合金的顺磁和铁磁奥氏体相的形成能(Eform)

Fig.2   Formation energies (Eform) of the paramagnetic and ferromagnetic austenites of the Ni8Mn4-xGa4Tix (x=0, 0.5, 1, 1.5 and 2) alloys

对Ni-Mn-Ga系铁磁形状记忆合金TC的模拟估算，一直是困扰研究者的难题。Velikokhatnyi和Naumov[37]根据Heisenberg模型和分子场理论计算的Ni2MnGa合金的TC (3943 K)与实测值(380 K)相差约10倍。根据Stoner理论[38,39]，顺磁奥氏体和铁磁奥氏体之间的总能差(ΔEtot)可以用来估计TC[40]。Chakrabarti等[41]指出，可以通过纯材料的实测值得到一个比例因子，进而预测不同掺杂浓度合金的TC。本工作将Chakrabarti等的方法引入到Ni-Mn-Ga-Ti合金TC的计算上。Brown等[35]使用中子衍射方法精确测定了Ni2MnGa的TC为365 K，在本工作对TC的估算中指定X0合金的TC等于365 K；ΔEtot为通过计算得到的顺磁奥氏体与铁磁奥氏体相的总能之差，详见表2所示。通过︱ΔEtot︱/ TC=常数可以计算Chakrabarti等提及的比例因子，并预测X0.5、X1、X1.5和X2合金的TC分别为314、263、212和162 K，如表2所示。本工作对TC的估算是在不考虑TC之上局域化的自旋磁矩和以自旋波形式存在的基本激发的情况下，仅从ΔEtot的角度得到的结论，即Ni8Mn4-xGa4Tix (即Ti掺杂含量为0~12.5%)合金的TC随着Ti含量的增加而显著降低，从365 K降低至162 K。而文献[23]基于Ni53Mn23.5Ga23.5-xTix (x为原子分数，0≤x≤5%)合金得到随着Ti含量的逐渐增加，合金的TC从约349 K急剧降低至252 K。本工作对TC的估算结果与实验观察[23]结果相一致，从理论上解释了该合金的TC随Ti含量升高而降低的物理本质为顺磁奥氏体与铁磁奥氏体的总能量之差的减小，即磁性转变的驱动力降低。但是TC急剧降低不利于实际应用，因此在实验中应严格控制Ti元素的添加量。

表2   Ni8Mn4-xGa4Tix (x=0、0.5、1、1.5和2)合金顺磁奥氏体和铁磁奥氏体的总能量(Etot (PA)和Etot (FA))和二者的能量差(ΔEtot)以及估算的Curie温度(TC)

Table 2  

新窗口打开| 下载CSV

2.3 磁性能和电子态密度

奥氏体母相的原子磁矩和总磁矩的计算结果列于表3中，并与文献[42,43]的数值进行比较。从表3可以看出，Mn是磁矩的主要贡献者(约3.065×10-23 A·m2)，而Ga和Ti的磁矩几乎为零。由于Ti的原子磁矩远小于Mn的原子磁矩。因此，当Mn逐渐被Ti取代时，合金的总磁矩显著降低，这也与实验观察结果相一致[23]。此外，Ni的原子磁矩从0.325×10-23 A·m2 (X0)急剧下降到约0.090×10-23 A·m2 (X2)，这主要是由于Mn含量降低引起的近邻的Ni和Mn之间3d电子相互作用减弱所致。在实验中应合理控制Ti元素的添加量，既要确保Ti掺杂可以析出适量的Ni3Ti弥散析出物以提高合金的力学性能，又要保证合适的TC和磁性能以利于实际应用。

表3   Ni8Mn4-xGa4Tix (x=0、0.5、1、1.5和2)合金奥氏体相的原子磁矩(MNi、MMn、MGa和MTi)和总磁矩(Mtot)的计算结果

Table 3  

新窗口打开| 下载CSV

为了进一步阐明Ti掺杂对合金的电子结构和磁性能的影响，在前述平衡晶格常数的基础上，用带有Bl?chl修正的四面体方法[44]，计算了X0、X1和X2合金的电子自旋总态密度和分波态密度(density of states，DOS)，分别如图3和4所示。Fermi能级(EF)被设置为坐标零点。

图3

图3   Ni8Mn4-xGa4Tix (x=0、1、2)合金奥氏体母相的自旋总电子态密度

Fig.3   Total density of states of ferromagnetic austenite for Ni8Mn4-xGa4Tix alloys with x=0 (a), x=1 (b) and x=2 (c) (EF—Fermi level. Circles in Fig.3 show that the intensity of up-spin total DOS (from -3.5 eV to -1 eV) decreases with the increasing content of Ti, and arrows in Fig.3 show that the intensity of the peak at 1.3 eV decreases with the Ti content in the down-spin total DOS)

图4

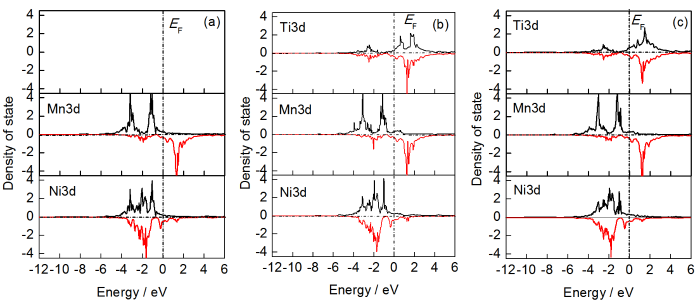
图4   Ni8Mn4-xGa4Tix (x=0、1、2)合金奥氏体母相的自旋分波态密度

Fig.4   Partial density of states of ferromagnetic austenite for Ni8Mn4-xGa4Tix alloys with x=0 (a), x=1 (b) and x=2 (c)

Zayak等[45]对Ni2MnGa合金的总态密度进行了详细的研究，本工作对Ni2MnGa的计算结果(图3a)与Zayak等的结果保持一致。通过比较图3中的自旋向上和自旋向下的电子态密度，注意到合金总磁矩的差异是由Fermi面以下自旋向上和自旋向下电子数之差的变化引起的。自旋向上的电子态密度(从-3.5 eV到-1 eV)的强度随着Ti含量的增加而显著减小(如图3中圆圈所示)，Fermi面以下的自旋向下部分变化不明显，从而导致自旋向上与自旋向下的电子数之差减小(对于X0、X1和X2合金，自旋向上和自旋向下的电子态密度之差分别为15.477、11.938和7.295个电子)，这是Ti含量增加而合金总磁矩显著降低的本质原因(X0、X1和X2合金的总磁矩分别为3.732×10-23、2.631×10-23和1.680×10-23 A·m2，见表3)。

从图4可以看出，Fermi面之下，分波态密度主要由位于-4 eV和Fermi面之间的Ni和Mn的 3d态电子成键支配，Ti的3d态也有少量贡献。在Fermi面之下Ti和Ni组分的3d自旋向上态密度的主峰位置重合(约-2 eV处)。这种效应是Ti和Ni原子之间3d电子能级杂化的结果。在Fermi面之上，Ti组分的3d自旋向上态密度有2个主峰，分别位于约0.8和1.5 eV处。而Mn和Ti的3d自旋向下态在Fermi能级以上占主导地位，主峰位于1.3 eV处。此外，在自旋向下总态密度图中观察到随Ti含量增加，位于1.3 eV处的主峰强度逐渐降低(如图3中箭头所示)，这主要是由Ti组分的3d分波态密度变化所致。

3 结论

本工作对Ni8Mn4-xGa4Tix (x=0、0.5、1、1.5和2)铁磁形状记忆合金的形成能、磁性能和电子结构进行第一性原理计算。结果表明，根据能量最低原理，添加的Ti优先占据Ni2MnGa合金中的Mn位。随着Ti含量的增加，奥氏体母相的平衡晶格常数逐渐增加；而四方马氏体相的a增加，c减小，导致马氏体四方度c/a比降低。用Ti取代Mn会导致顺磁和铁磁奥氏体相稳定性升高。随着Ti含量的增加，顺磁奥氏体与铁磁奥氏体相的总能之差减小，从本质上导致了实验观察到的合金Curie温度的降低。随着Ti含量的逐渐增加，Fermi面以下自旋向上总电子态密度逐渐降低，而自旋向下的部分几乎不变，导致自旋向上与自旋向下的电子数之差减小，这是Ti含量增加而合金总磁矩降低的本质原因。在实验中应合理控制Ti元素的添加量，既要确保Ti掺杂可以析出适量的Ni3Ti弥散析出物以提高合金的力学性能，又要保证合适的Curie温度和磁性能以利于实际应用。

来源--金属学报