分享：TiNi合金B2奥氏体中Ti位Ni诱导的晶格失稳

牛建钢1, , 肖伟2

1 河北大学机械系 保定 071002
2 北京科技大学材料科学与工程学院 北京 100083

摘要

关键词： TiNi合金 ; 晶格失稳 ; 第一原理

形状记忆合金以其特有的形状记忆效应、超弹性性质,在多种工业领域具有很大应用潜力。虽然TiNi合金中形状记忆效应的发现[1]晚于AuCd合金[2],但由于其出色的形状记忆效应和综合力学性能,成为了形状记忆合金的典型代表。

形状记忆合金的形状记忆效应和超弹性只在正、逆马氏体相变温度区间存在,因此对马氏体相变温度的控制是应用形状记忆合金的一个关键问题。一般来说,价电子浓度被认为决定着TiNi合金[3]以及钛基、锆基等过渡金属合金[4,5,6,7,8]的相稳定性/相变温度。奇怪的是,在等原子比TiNi合金的基础上,Ni含量每增加1% (原子分数)后,虽然增加的价电子浓度小于0.002,但马氏体相变温度急剧下降150 K[9,10,11]。这种超常规的相变温度降低幅度不但超过TiNi合金中Fe、Mn等元素的影响,即使在结构材料中也很罕见。对这一异常现象的合理解读成为TiNi合金相变的一个难题。正是考虑到富Ni成分TiNi合金与价电子规律相悖,Frenzel等[12]提出,应把TiNi合金分为2大类：价电子单因素影响和非价电子单因素影响。

最近,第一原理计算已经复现了富Ni成分TiNi合金[12]和含Fe成分TiNi合金[13]的马氏体相变温度随Ni、Fe浓度的变化趋势,为理解这一问题提供了理论基础。计算表明,二者最大区别是前者奥氏体中Ti位Ni可以引起明显畸变而后者中的Ni位Fe不具此作用。Ti位Ni增加1% (原子分数),畸变可以显著降低奥氏体与马氏体的能量差异达10 meV/atom,相当于降低马氏体相变温度达120 K[12]。因此,理解Ti位Ni的几何畸变作用就成为了解TiNi合金以及更多同类形状记忆合金相变温度规律的一个新要求。

局域软模理论认为,缺陷周围的畸变可能令局域弹性软化,以至到达能够令相变自动进行的应变失稳(strain spinodal),导致局域晶格失稳[14]。奥氏体的局域晶格失稳意味着此区域开始马氏体/类马氏体形核进程[14]。由于局域马氏体/类马氏体的能量低于奥氏体母相,因此可以在全局上降低奥氏体相能量以及降低奥氏体与马氏体的能量差异,从而降低马氏体相变温度。基于以上认识,可以猜想TiNi合金中Ti位Ni畸变引起了奥氏体局域失稳,帮助降低马氏体相变温度。尤其晶格稳定性与弹性存在关联性[15],在弹性软化系统中倾向失稳,而TiNi合金奥氏体随温度降低出现弹性软化特征[16],会增大失稳倾向。本工作主要目的是检验Ti位Ni是否引起了奥氏体局域晶格失稳,从而证实以上猜想,进而深入理解非价电子单因素影响的TiNi合金以及同类形状记忆合金的相变温度规律。

失稳总是沿着从高自由能向低自由能的方向进行,所以比较点缺陷畸变前后的能量[17]一定程度上可以帮助判断畸变与晶格失稳的联系。在此基础上,考虑到晶格失稳的外在表现是晶格对于特定变形的恢复力为零,本工作进一步提出第一原理计算框架内的点缺陷扰动策略,通过观察点缺陷畸变是否恢复以检验点缺陷是否造成晶格失稳。特别要强调的是：依据应变核胚理论[18],失稳产物可以是任意结构,而不一定是马氏体。点缺陷扰动策略的优势之一就在于并不预设失稳终态相结构,而是经几何优化寻找能量最低结构,从而有效预测失稳终态相结构。

1 计算模型与方法

1.1 点缺陷扰动策略

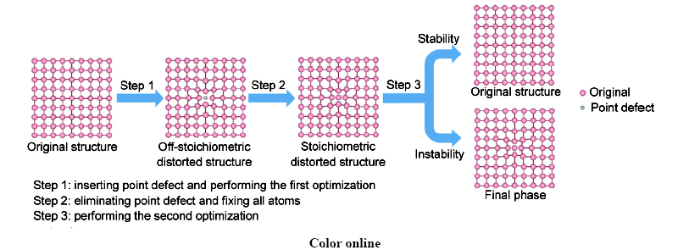
图1对点缺陷扰动策略做了示意性描述。第1步：将点缺陷置入初始晶胞,进行第一原理几何优化计算,得到的是非等原子比畸变结构;第2步：消除点缺陷,固定所有原子位置,得到等原子比畸变结构;第3步：再次几何优化,优化后若结构不能恢复到初始结构,表示初始结构已经失稳,所得结构即为失稳的终态相。本工作中的点缺陷为Ti位Ni,初始结构为TiNi合金的B2奥氏体或B19′马氏体。

图1   点缺陷扰动策略示意图

Fig.1   Schematic demonstration of point defect perturbation strategy

1.2 计算晶胞

TiNi合金奥氏体被广泛接受为B2结构[19]。B2原胞为晶格常数0.300 nm的立方晶胞,包含1个占据角位的Ti原子和1个占据体心的Ni原子。本工作计算使用了2类B2-TiNi超晶胞：(1) 原胞直接倍增形成的 $2\times 2\times 2$、 $3\times 3\times 3$、 $4\times 4\times 4$、 $5\times 5\times 5$立方超晶胞;(2) 由(111)B2面沿[111]B2方向叠加形成的六方超晶胞,晶胞a、b、c轴为[101]B2、[011]B2、[111]B2晶向。六方超晶胞的最小晶胞为6原子的 $\sqrt[]{2}\times \sqrt[]{2}\times \sqrt[]{3}$晶胞,其余晶胞是 $\sqrt[]{2}\times \sqrt[]{2}\times \sqrt[]{3}$晶胞的 $1\times 1\times 2$、 $1\times 1\times 3$、 $1\times 1\times 4$、 $2\times 2\times 1$、 $2\times 2\times 2$、 $3\times 3\times 1$、 $3\times 3\times 3$超晶胞,即 $\sqrt[]{2}\times \sqrt[]{2}\times 2\sqrt[]{3}$、 $\sqrt[]{2}\times \sqrt[]{2}\times 3\sqrt[]{3}$、 $\sqrt[]{2}\times \sqrt[]{2}\times 4\sqrt[]{3}$、 $2\sqrt[]{2}\times 2\sqrt[]{2}\times \sqrt[]{3}$、 $2\sqrt[]{2}\times 2\sqrt[]{2}\times 2\sqrt[]{3}$、 $3\sqrt[]{2}\times 3\sqrt[]{2}\times \sqrt[]{3}$、 $3\sqrt[]{2}\times 3\sqrt[]{2}\times 3\sqrt[]{3}$晶胞。

B19′马氏体是TiNi合金中最常被观察到的马氏体。B19′相属单斜晶系,原胞晶格常数a=0.291 nm、b=0.471 nm、c=0.404 nm,α=β=90°,γ=100°,包含2个Ti原子和2个Ni原子。本工作计算使用了3×1×2、2×2×2、3×2×2、4×2×2、3×3×3、4×2×4、4×3×3共7个B19′-TiNi超晶胞。

1.3 Ti位Ni超点阵

TiNi合金B2奥氏体中点缺陷具有明显的相互作用[20]。因此本工作在计算奥氏体中Ti位Ni时,通过构建具有不同空间对称性的Ti位Ni超点阵,最大程度涵盖Ti位Ni的空间分布和浓度,以体现Ti位Ni相互作用的影响。文中共考虑简单立方、bcc、fcc、简单六方4种Ti位Ni超点阵：(1) 简单立方超点阵：2×2×2、3×3×3、4×4×4、5×5×5立方超晶胞内各含1个Ti位Ni,对应Ti位Ni浓度(原子分数,下同)为6.0%、1.9%、0.8%、0.4%;(2) bcc超点阵：2×2×2和4×4×4立方超晶胞内各含2个Ti位Ni,分别位于角位和体心,对应Ti位Ni浓度为13.0%和1.6%;(3) fcc超点阵：2×2×2和4×4×4立方超晶胞内含4个Ti位Ni,分别位于角位和面心,对应Ti位Ni浓度为25.0%和3.0%;(4) 简单六方超点阵： $\sqrt[]{2}\times \sqrt[]{2}\times 2\sqrt[]{3}$、 $\sqrt[]{2}\times \sqrt[]{2}\times 3\sqrt[]{3}$、 $\sqrt[]{2}\times \sqrt[]{2}\times 4\sqrt[]{3}$、 $2\sqrt[]{2}\times 2\sqrt[]{2}\times \sqrt[]{3}$、 $2\sqrt[]{2}\times 2\sqrt[]{2}\times 2\sqrt[]{3}$、 $3\sqrt[]{2}\times 3\sqrt[]{2}\times \sqrt[]{3}$、 $3\sqrt[]{2}\times 3\sqrt[]{2}\times 3\sqrt[]{3}$六方超晶胞内含1个Ti位Ni,对应Ti位Ni浓度为17.0%,8.0%、4.0%、4.0%、2.0%、1.9%、0.6%。

图2a~d所示依次为2×2×2立方超晶胞的简单立方、bcc、fcc Ti位Ni超点阵和 $\sqrt[]{2}\times \sqrt[]{2}\times \sqrt[]{3}$六方晶胞的简单六方Ti位Ni超点阵。

图2   2×2×2的B2超晶胞中简单立方、bcc、fcc Ti位Ni超点阵和$\sqrt[]{2}\times \sqrt[]{2}\times \sqrt[]{3}$的B2超晶胞中简单六方Ti位Ni超点阵

Fig.2   Simple cubic (a), bcc (b) and fcc (c) Ti-site-Ni superlattices in 2×2×2 B2 supercells and simple hexagonal (d) Ti-site-Ni superlattice in $\sqrt[]{2}\times \sqrt[]{2}\times \sqrt[]{3}$ B2 supercell

3×1×2、2×2×2、3×2×2、4×2×2、3×3×3、4×2×4、4×3×3的B19′超晶胞内只包含1个Ti位Ni,分别对应4.0%、3.0%、2.0%、1.6%、0.9%、0.8%、0.7% Ti位Ni浓度。

1.4 第一原理计算

计算由VASP软件包完成[21]。电子相互作用使用投影缀加平面波描述[22]。交换关联势采用广义梯度近似(GGA)的Perdew-Burke-Ernzerhof (PBE)势[23]。平面波截断能量为350 eV。Methfessel-Paxton的smearing数值设为0.1 eV。对于2×2×2立方超晶胞和 $\sqrt[]{2}\times \sqrt[]{2}\times \sqrt[]{3}$六方超晶胞,按照Monkhorst-Pack方法[24]分别设置K点网格为5×5×5 和8×8×6,其余晶胞K点网格按晶胞尺寸比例倍减。几何优化计算中优化原子坐标,固定晶胞尺寸。经过对0.8%、4.0%、17.0% Ti位Ni浓度晶胞进行测试,同时对晶胞尺寸与原子坐标几何优化所得能量与固定晶胞尺寸所得能量的差异不超过1 meV/atom。计算中能量的收敛标准设为1×10-4 eV。

2 计算结果分析

2.1 奥氏体中Ti位Ni

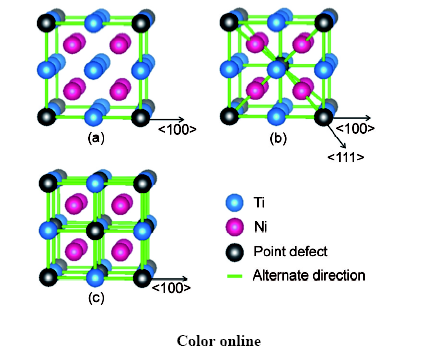
2.1.1 晶格失稳 除最小立方晶胞——2×2×2晶胞之外,无论Ti位Ni按何种超点阵分布,B2结构扰动后均不再回复到初始结构,即初始的B2结构已经失稳,这直接证实了本工作提出的Ti位Ni诱导奥氏体晶格失稳的猜想。就2×2×2晶胞不失稳问题,可做如下理解。如图3所示,Ti位Ni组成简单立方(图3a)、fcc (图3c)超点阵时,2×2×2晶胞中Ti位Ni和第2近邻Ti原子沿<100>方向交替;Ti位Ni组成bcc (图3b)超点阵时,2×2×2晶胞中Ti位Ni沿<111>、 <100>晶向分别与第1、2近邻Ti原子交替。原子交替导致Ti位Ni在该晶向上对近邻原子的扰动效果相互抵消,导致2×2×2晶胞不失稳。后面的讨论聚焦于失稳晶胞,将不再考虑2×2×2晶胞。

图3   2×2×2晶胞中简单立方、bcc、fcc超点阵Ti位Ni和近邻原子的交替分布

Fig.3   The alternation of simple cubic (a), bcc (b) and fcc (c) superlattice Ti-site Ni and its neighbor atoms in 2×2×2 supercells

2.1.2 失稳终态相

(1) 能量

图4为失稳终态相与B2相的能量差(ΔEfinal-B2)随Ti位Ni浓度的变化。由图可见,ΔEfinal-B2范围为-20~0 meV/atom,即失稳终态相总是比B2相更稳定。这也就是发生失稳的驱动力。ΔEfinal-B2最低为-20 meV/atom,高于已知的B19′ (-46 meV/atom)马氏体,即失稳终态相不如已知的马氏体稳定。为清晰观察ΔEfinal-B2随Ti位Ni浓度的变化趋势,图4中用虚线标识出了ΔEfinal-B2下限。ΔEfinal-B2下限随Ti位Ni浓度先下降后上升,最低能量(-20 meV/atom)出现在Ti位Ni浓度2.0%和4.0%,对应晶胞分别是简单六方Ti位Ni超点阵的 $2\sqrt[]{2}\times 2\sqrt[]{2}\times 2\sqrt[]{3}$晶胞和 $2\sqrt[]{2}\times 2\sqrt[]{2}\times \sqrt[]{3}$晶胞。

图4   失稳终态相与B2相的能量差(ΔEfinal-B2)随Ti位Ni浓度的变化

Fig.4   Changes of the energetic difference between final phase and B2 phase (ΔEfinal-B2) with Ti-site Ni content

(2) 结构

不同计算晶胞的Ti位Ni超点阵对称性或基矢存在差异。这也就导致各晶胞结构并不一致(也因此图4中能量数值不唯一)。但失稳终态相晶胞均体现出共同的结构特征：围绕扰动位的一维上<111>B2方向原子列膨胀与<100>B2方向原子列收缩。下面以具有代表性的5×5×5、 $2\sqrt[]{2}\times 2\sqrt[]{2}\times \sqrt[]{3}$、 $\sqrt[]{2}\times \sqrt[]{2}\times \sqrt[]{3}$晶胞为例对此结构特征进行具体说明。这3个晶胞的能量为-8、-20、-8 meV/atom,均是图4中的能量下限。同时,这3个晶胞各包含一个扰动Ti位Ni,对应浓度是0.4%、4.0%、17.0%,分别是所有失稳晶胞中的最低浓度、居中浓度、最高浓度。另外,它们也分别是所有失稳晶胞中最大晶胞、能量最低晶胞、最小晶胞。

图5a是失稳终态相与B2相在5×5×5晶胞中的键长差异(ΔLfinal-B2)。与B2相相比,失稳终态相的扰动位原子与<111>B2晶向上第1、5、10近邻间的键长显著增大(对应正值ΔLfinal-B2),增幅大于或接近0.02 nm。反之,扰动位原子与<100>B2晶向上第2、6近邻间的键长显著减小(对应负值ΔLfinal-B2),减幅也大于0.02 nm。另一方面,扰动位原子与其它晶向上的第3、4、7、8、9近邻间的键长变动很小,变化幅度小于0.005 nm。因此,其结构特征可以总结成：围绕扰动位的一维上<111>B2方向原子列膨胀与<100>B2方向原子列收缩。值得注意的是,如果从软化的奥氏体弹性系数c′和c44判断[16],TiNi合金奥氏体中发生的主要是二维上的{110}晶面剪切失稳[15,25]。但Ti位Ni失稳的一维特征与之明显不同。

图5   失稳终态相与B2相在$5\times 5\times 5$晶胞和$2\sqrt[]{2}\times 2\sqrt[]{2}\times \sqrt[]{3}$晶胞中的键长差异(ΔLfinal-B2)

Fig.5   The differences of bond lengths between final phase and B2 phase (ΔLfinal-B2) in 5×5×5 (a) and $2\sqrt[]{2}\times 2\sqrt[]{2}\times \sqrt[]{3}$(b) cells (Plus and negative mean elongation and compression respectively, P and n represent perturbation site atom and neighbor, respectively)

图5b是失稳终态相与B2相在 $2\sqrt[]{2}\times 2\sqrt[]{2}\times \sqrt[]{3}$晶胞中的键长差异(ΔLfinal-B2)。与图5a稍微不同的是, $2\sqrt[]{2}\times 2\sqrt[]{2}\times \sqrt[]{3}$晶胞中沿c轴方向扰动位原子与第1近邻原子交替,不产生扰动后果,因此图5b只统计涉及非c轴第1近邻的键长。由图5b可见,相对于初始B2相,失稳终态相同样围绕扰动位呈现<111>B2方向原子列膨胀与<100>B2方向原子列收缩的特征,并且第1、2近邻膨胀和收缩幅度大于0.02 nm,与5×5×5晶胞相当。由于 $2\sqrt[]{2}\times 2\sqrt[]{2}\times \sqrt[]{3}$晶胞的Ti位Ni浓度为4.0%,是5×5×5晶胞(0.4%)的10倍,因此被扰动的近邻原子浓度也为5×5×5晶胞的10倍。这意味着二者在失稳结构相近的前提下 $2\sqrt[]{2}\times 2\sqrt[]{2}\times \sqrt[]{3}$晶胞失稳范围更大,也因此能量更低,乃至在所计算全部晶胞中, $2\sqrt[]{2}\times 2\sqrt[]{2}\times \sqrt[]{3}$晶胞能量最低。

$\sqrt[]{2}\times \sqrt[]{2}\times \sqrt[]{3}$晶胞中的键长差异明显小于 $2\sqrt[]{2}\times 2\sqrt[]{2}\times \sqrt[]{3}$晶胞以及5×5×5晶胞：扰动位原子与第1、2近邻间的键长分别增大0.008 nm和减小0.016 nm。这说明其原子列膨胀与收缩的特征不如前2者明显。也因此虽然被扰动的近邻原子浓度大于 $2\sqrt[]{2}\times 2\sqrt[]{2}\times \sqrt[]{3}$晶胞,但能量却较之更高。

2.1.3 畸变

(1) 能量

图6为等原子比畸变结构与B2相的能量差(ΔEdistorted-B2)随Ti位Ni浓度的变化。作为对比,图6中同时给出失稳终态相与B2相的能量差ΔEfinal-B2。图中虚线仍标示下限。图6的主要特征是ΔEdistorted-B2与ΔEfinal-B2的相似性,具体表现在：(1) 二者下限虚线随Ti位Ni浓度的变化趋势相同,均先下降再上升,最低能量均位于在Ti位Ni浓度2%和4%区域(并且同样对应 $2\sqrt[]{2}\times 2\sqrt[]{2}\times 2\sqrt[]{3}$和 $2\sqrt[]{2}\times 2\sqrt[]{2}\times \sqrt[]{3}$晶胞);(2) 当Ti位Ni浓度小于4.0%时,二者下限虚线的数值均为负,而且差异小于5 meV/atom。ΔEdistorted-B2的能量下限为负意味着B2奥氏体中Ti位Ni畸变能获得能量收益。而如果马氏体中Ti位Ni畸变不获得能量收益或能量收益较少,那么Ti位Ni只依靠畸变就可以提高奥氏体相对马氏体的稳定性,从而降低相变温度,这就是Ti位Ni失稳影响相变温度的直接原因。

图6   畸变结构与B2相的能量差(ΔEdistorted-B2)和失稳终态相与B2相的能量差(ΔEfinal-B2)的对比

Fig.6   The comparison of the energetic difference between distorted structure and B2 phase (ΔEdistorted-B2) and the energetic difference between instability final phase and B2 phase (ΔEfinal-B2)

既然从点缺陷扰动步骤(图1)来看,失稳终态相结构是畸变结构优化后的最优结构,那么后者必然能量更高。所以图6中ΔEdistorted-B2的数值始终大于ΔEfinal-B2。而且当Ti位Ni浓度大于4.0%时,ΔEdistorted-B2的能量下限甚至开始高于B2结构,即畸变结构的稳定性开始弱于B2结构。

(2) 结构

与失稳终态相相同,畸变结构的各晶胞结构并不一致。Frenzel等[12]首次报道了Ti位Ni畸变结构特征：与B2结构相比,Ti位Ni第1近邻原子膨胀和第2近邻原子收缩。由此可知,畸变结构具有和失稳终态相相似的特征。为进一步明确二者在结构上的相似程度,图7给出了全部晶胞的畸变结构与失稳终态相键长之差(ΔLdistorted-final)。可见,在绝大部分Ti位Ni浓度下,二者的扰动位和第1近邻的键长差异小于或等于0.01 nm。而作为对照,失稳终态相和B2结构的扰动位与第1近邻的键长差异大于0.03 nm (图5)。也正是源于这一结构上的相似性,才决定了畸变结构和失稳终态相在能量上的相似性(图6)。

由图7可见,除0.4%Ti位Ni浓度外,扰动位与第一近邻的ΔLdistorted-final均为正,扰动位与第二近邻的ΔLdistorted-final均为负。这意味着畸变结构中的第1、2近邻膨胀与收缩程度大于失稳终态相,即畸变结构沿失稳方向的应变比终态相更显著。从应变失稳的角度,这也就意味着Ti位Ni畸变必然使B2晶格失稳发生。

图7   畸变结构与失稳终态相之间的键长差异(ΔLdistorted-final)

Fig.7   The bond length difference between distorted structure and final phase (ΔLdistorted-final)

2.2 马氏体中Ti位Ni

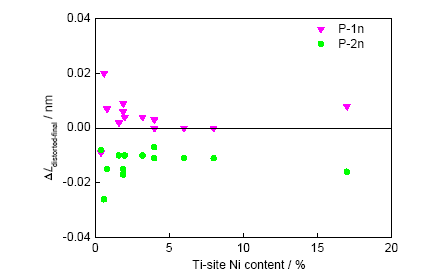
为了对比马氏体与奥氏体中Ti位Ni的表现,本工作以B19′马氏体作为初始结构,进行了Ti位Ni扰动计算。计算结果表明,马氏体中Ti位Ni并未引起失稳。与之相联系,B19′相的等原子比畸变结构也就不会因为趋近失稳终态相而获得能量收益。以上结果均与B2奥氏体中的Ti位Ni表现相反。为了展示此差异,图8对比了ΔEdistorted-B19′和ΔEdistorted-B2,前者为B19′相的等原子比畸变结构和初始B19′结构能量差,后者为B2相的等原子比畸变结构与初始B2结构的能量差。为更清晰,图8只给出了ΔEdistorted-B2下限。由图可见,ΔEdistorted-B19′和ΔEdistorted-B2分别为正、负值,差异显著。而且二者差异随Ti位Ni浓度每增大1% (原子分数)就增大约10~15 meV/atom。

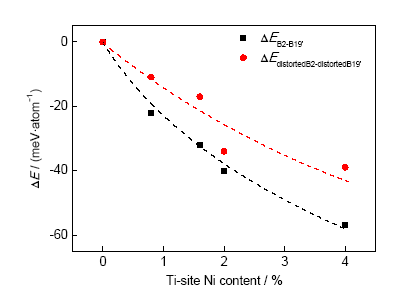
为了进一步考量B2相和B19′相的畸变差异对马氏体相变温度的影响,图9比较了ΔEdistortedB2-distortedB19′和ΔEB2-B19′,前者为B2相和B19′相的等原子比畸变结构(不包含Ti位Ni)能量差,后者为B2相和B19′相(包含Ti位Ni)的能量差。ΔEB2-B19′对应马氏体相变温度,ΔEB2-B19′越小,相变温度越低。它包含结构变化的影响与化学作用的影响2个部分,ΔEdistortedB2-distortedB19′就代表了其中结构变化的影响。为便于比较,图9设Ti位Ni零浓度时ΔEB2-B19′为零,即只讨论ΔEB2-B19′随Ti位Ni浓度的变化,而不考虑绝对值。同样,也只考虑ΔEdistortedB2-distortedB19′随Ti位Ni浓度的变化,相当于ΔEdistorted-B2和ΔEdistorted-B19′的差值。由图9可见,当Ti位Ni浓度小于2% (原子分数)时,随Ti位Ni浓度每增大1%,ΔEB2-B19′降低约20 meV/atom。根据能量差(ΔE)与相变温度(T)的关系T=ΔE/kB (kB是Boltzmann常数),这相当于Ti位Ni浓度每增大1%相变温度降低约230 K。这与之前的计算结果[12]一致。等原子比TiNi合金的马氏体相变温度为330 K[9,10,11],也就是说2%Ti位Ni浓度已足以将相变温度降低为零,所以图8和9均不再展示更高Ti位Ni浓度。随Ti位Ni浓度每增大1% (原子分数),ΔEdistortedB2-distortedB19′降低约10~15 meV/atom,占ΔEB2-B19′的50%~75%。这表明ΔEdistortedB2-distortedB19′对ΔEB2-B19′及其所对应的马氏体相变温度变化有明显贡献。

图8   畸变B19′相结构与B19′相的能量差(ΔEdistorted-B19′)和畸变B2相结构与B2相的能量差(ΔEdistorted-B2)的对比

Fig.8   The comparison of the energetic difference between distorted B19′ structure and B19′ phase (ΔEdistorted-B19′) and energetic difference between distorted B2 structure and B2 phase (ΔEdistorted-B2)

图9   畸变B2相结构与畸变B19′相结构的能量差(ΔEdistortedB2-distortedB19′)和B2相与B19′相的能量差(ΔEB2-B19′)的对比

Fig.9   The comparison of the energetic difference between distorted B2 structure and distorted B19′ structure (ΔEdistortedB2-distortedB19′) and energetic difference between B2 phase and B19′ phase (ΔEB2-B19′)

3 结论

(1) 提出第一原理计算框架内的点缺陷扰动策略,可用来证实点缺陷是否导致初始结构失稳,并预测失稳终态相结构。

(2) 通过点缺陷扰动策略,证实TiNi合金中Ti位Ni会诱导奥氏体晶格失稳。不同于更常见的{110}晶面剪切失稳,Ti位Ni失稳终态相主要结构特征为从扰动位出发的一维方向上<100>B2原子列收缩和<111>B2原子列膨胀。失稳终态相的能量低于B2相,最低能量比B2相低20 meV/atom,在Ti位Ni浓度达到2%~4%时出现。

(3) 与奥氏体的情况相反,Ti位Ni无法令马氏体晶格失稳。由此导致奥氏体和马氏体的畸变结构能量差异显著。此一差异对TiNi合金马氏体相变温度变化的贡献可达50%以上。

来源--金属学报