分享:镍基变形高温合金动态软化行为与组织演变规律研究
王涛
摘要
采用Gleeble3500D热模拟试验机研究了GH4720Li合金的高温热变形行为,分析了不同热压缩工艺条件下流变力学曲线特征,建立了表征材料流变力学特征的包含应变参量的双曲正弦型Arrhenius本构关系模型以及BP人工神经网络模型,并通过对材料热变形组织的表征,揭示了GH4720Li合金高温变形过程中的动态再结晶形核机制。结果表明,包含应变参量的双曲正弦型Arrhenius本构关系模型预测精度较差,而BP人工神经网络模型能很好地表征GH4720Li合金热变形过程中的流变力学行为,模型预测值与实验值的平均相对误差仅为0.814%。组织分析结果表明,GH4720Li合金在1140 ℃条件下动态再结晶的主要形核机制为非连续动态再结晶,变形晶粒的晶界为再结晶晶粒提供形核位置。
关键词:
伴随着航空发动机工作效率的提升,其对关键部件材料的力学性能以及耐高温性能的要求不断提高,燃气涡轮发动机涡轮盘、高压压气机盘作为关键转动部件,一直以来是研究的重点和热点。作为上一代燃气涡轮发动机涡轮盘的首选材料,GH4169合金由于受到亚稳态γ''相的限制,其最高使用温度不超过650 ℃[1~3],与γ''强化型GH4169合金相比,高含量γ'强化型GH4720Li合金的组织稳定性和服役温度得到了显著的提升[4,5],然而高含量的强化相显著降低了GH4720Li合金的热加工性能,给其微观组织和力学性能控制带来了很大的难度。由于GH4720Li合金具有优异的高温力学性能,其应用范围不断扩大,已成为国内外学者的研究热点[6~8]。
通常,金属材料在热变形过程中还常常伴随着一系列的冶金现象,如:加工硬化行为以及动态回复和动态再结晶等软化效应[9,10],热变形参数(应变速率、形变温度以及变形量)通过控制材料在热成形过程中的加工硬化和动态软化效应,从而控制材料的流变力学行为。等温热模拟压缩实验是一种有效的分析材料在热成形过程中流变力学行为的技术手段,通过对实验所获得的真实应力-应变曲线进行分析,并建立预测精度较高的表征材料变形过程中真实应力与热变形参数之间本构关系的模型,是实现材料成形过程中有限元模拟的关键环节。目前,在金属材料高温变形行为本构关系模型研究方面,国内外学者通常采用唯象形本构关系模型、半经验本构关系模型以及人工智能本构关系模型,而其中双曲正弦型Arrhenius本构关系模型以及BP人工神经元网络模型最受认可[11~13]。Pu等[14]研究了S32654超级奥氏体不锈钢热变形过程中的本构关系模型,通过将本构关系模型中的材料常量与应变进行8次多项式拟合,建立了包含应变参量的双曲正弦型Arrhenius本构关系模型,其平均相对误差绝对值为5.2%。Li等[15]采用修正的包含应变参量的Arrhenius本构关系模型和人工神经元网络模型描述了Al-Zn-Mg合金的流变力学行为,结果表明人工神经元网络模型的预测精度较高,其相关系数以及平均相对误差绝对值分别为0.9987和0.58%,此外其还兼具与有限元模拟软件耦合性好的优点。
目前对GH4720Li合金的研究主要集中在二次相形貌以及沉淀机制[16,17]、室温以及高温条件下初始组织对疲劳裂纹萌生与扩展行为的影响[18,19]、热处理工艺对其组织以及力学性能影响规律等方面[20,21],而对高温变形行为尤其热变形本构关系研究方面鲜有报道。本工作发现,采用Arrhenius模型的预测精度较差,不能很好地预测材料在热变形过程中的流变力学行为。因此,在本工作中以GH4720Li合金热模拟压缩实验得到的流变力学曲线为依据,分析了热变形参数对GH4720Li合金流变力学行为的影响规律,确定了不同应变条件下材料变形激活能,构建了包含应变参量的双曲正弦型Arrhenius模型以及BP人工神经网络模型,并通过对热变形组织的分析,揭示了材料热变形过程中动态再结晶的形核机制。
本实验采用的材料为锻造态GH4720Li高温合金,合金采用真空感应熔炼+保护气氛电渣重熔+真空自耗重熔三联冶炼工艺制备,经镦拔开坯后得到直径200 mm棒材。GH4720Li合金主要名义化学成分(质量分数,%)为:C 0.018,Cr 15.94,Co 14.5,W 1.25,Mo 2.94,Al 2.56,Ti 4.91,B 0.012,Zr 0.03,Ni 余量。可以看出,合金中Al+Ti元素含量高达7.5%。在Gleeble3500D热力模拟试验机上进行等温、恒应变速率单道次压缩实验,热压缩实验选用直径10 mm×15 mm的圆柱形标准热压缩试样。为减小压缩实验过程摩擦力的影响,在夹头与试样端面之间放置薄厚均匀的片状石墨片。试样以10 ℃/s的加热速率升高到变形温度为1060、1080、1100、1120和1140 ℃,为使试样各部位温度分布均匀,保温7 min,分别以0.001、0.01、0.1和1 s-1的变形速率进行等温压缩实验,最大应变0.8,变形后立即水冷以保留材料热成形后高温组织,变形后的组织采用20 mL HCl+30 mL CH3COOH+3 g CuCl2混合溶液对热变形试样进行化学腐蚀,并用DM6000M金相显微镜(OM)进行微观组织观察。
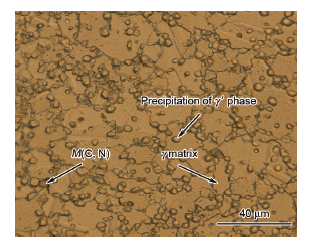
图1所示为GH4720Li合金棒材锻态初始组织的OM像。可以看出,基体γ相的平均晶粒尺寸约为17 μm,晶界上分布有尺寸约为3.2 μm的颗粒状一次γ'相。
图1 锻造态GH4720Li合金组织的OM像
Fig.1 OM image of as-forged GH4720Li alloy
图2给出了GH4720Li合金不同热变形参数条件下真实应力-应变曲线。可以看出,同一变形温度与应变速率条件下,随应变增加流变应力呈现出先增加后减小最终趋于稳定的变化趋势,该行为主要受热变形过程中的一系列冶金现象(加工硬化、动态回复以及动态再结晶)的影响[22,23]。在热变形初期,由于动态软化效应较弱,位错的增殖使得位错密度迅速增加,流变应力快速升高,伴随着应变的增加,动态回复引发的位错之间的交互作用逐渐增强,位错密度增速降低,流变应力呈现出缓慢增加的变化趋势,当位错密度增加至发生动态再结晶的临界密度时,动态软化作用进一步增强[24,25]。当流动应力达到峰值时,动态软化与加工硬化第一次达到动态平衡。当应变大于峰值应变时,应力随着应变的增加而降低,呈现出显著的动态软化特征,当加工硬化与动态软化达到第二次动态平衡时,流变应力逐渐趋于稳定[26,27]。
图2 GH4720Li合金在不同工艺参数条件下的应力-应变曲线
Fig.2 Stress-strain (σ-ε) curves of GH4720Li alloy at various hot processing parameters of 0.1 s-1 (a) and 1060 ℃ (b)
此外,在应变速率为0.1 s-1条件下,流变应力对温度的敏感性也有所不同,当热变形温度高于1100 ℃时,流变应力对温度的敏感性显著降低,当变形温度由1080 ℃升高至1100 ℃时,2变形条件下峰值应力之差为23 MPa,而变形温度由1120 ℃升高至1140 ℃时,该数值仅为7 MPa。这是因为随着温度的升高,晶界以及晶内的一次γ'相逐渐回熔,使得一次γ'沉淀相的尺寸以及数量均有所减小[5],从而其对晶界迁移和位错滑移的阻碍作用减弱,细晶强化效应减弱而动态软化效应增强,因此,当变形温度高于1100 ℃时,材料的流动应力显著降低。
双曲正弦型Arrhenius本构关系模型是一种用来描述材料在热塑性成形过程中流变力学行为的数学模型,通常金属材料流变应力与热变形参数之间的关系可以表示为[12~15]:
式中,为应变速率(s-1);α为材料应力水平常数;σ为真实应力(MPa);n为应力指数;Q为热变形激活能(kJ/mol),是热变形过程中表征原子重新排列难易程度的参量;R为气体常数(R=8.413 J/(molK));T为热力学温度(K);A、A1、A2、β和n1为与温度无关的常数,且α、β和n1之间的关系可以表示为α=n1/β;Z为温度补偿应变速率Zener-Hollomon参数。
当温度恒定的条件下,对式(1)和(2)两侧同时取对数得到:
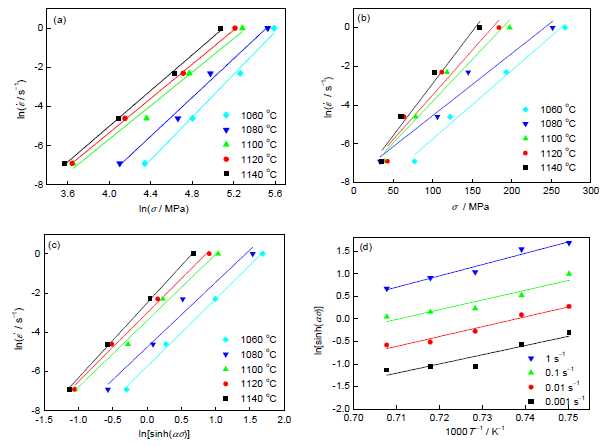
图3a和b分别给出了GH4720Li合金应变为0.1条件下ln-lnσ和ln-σ之间的关系曲线,图3a和b中曲线的斜率分别为n1和β。对图中不同温度下拟合直线的斜率取平均值,可得到n1=0.042,β=4.72,α= n1/β=0.0089。
对式(3)两侧分别取自然对数可得:
温度恒定时,式(7)两侧同时对求偏导得:
应变速率一定,式(7)两侧对1/T求偏导得:
假定
(10)
图3c和d分别给出了ln-ln[sinh(ασ)]和ln[sinh(ασ)]-1000/T之间的关系曲线。可以看出,2组曲线均呈现出较好的线性关系,图中斜率分别表示n和b。对拟合直线的斜率取平均值可得n=3.45,b=22.41。综合上述分析可得到GH4720Li合金应变为0.1条件下的热变形激活能为Q=Rnb=642.82 kJ/mol。
图3 GH4720Li合金ln-lnσ、ln-σ、ln-ln[sinh(ασ)]和ln[sinh(ασ)]-1000/T关系曲线
对式(4)两侧取自然对数可得:
将所求得Q、α、n以及T、、σ数值带入式(11),即可绘制lnZ-ln[sinh(ασ)]关系曲线,如图4所示,图中直线截距为lnA=53.63。通过上述过程,即可求解得到应变为0.1时本构模型中的材料常数:α=0.0089、n=3.45、lnA=53.63、Q=642.82 kJ/mol。
图4 GH4720Li合金lnZ与ln[sinh(ασ)]关系曲线
重复式(5)~(11)所描述的分析过程,求解得到应变从0.1至0.8每间隔0.05条件下Arrhenius本构关系模型中的材料常数,对本构关系模型中材料参数与应变做不同阶数的多项式拟合,建立了拟合相关系数随多项式拟合阶数关系曲线,如图5所示。可以看出,随着拟合阶数的增加,拟合结果的相关系数先显著增加,达到某一峰值后逐渐趋于稳定或略微降低。因此,为提高预测精度,并兼顾计算效率因素,分别采用阶数为6、7、8以及7次多项式对Arrhenius本构关系模型中α、Q、n和lnA进行拟合,得到模型参数与应变之间的关系曲线。
图5 GH4720Li合金材料参数随应变以及相关系数随拟合阶数变化曲线
Fig.5 Relationships between material constant α (a), Q (b), n (c), lnA (d) and strain, as well as correlation coefficient and polynomial order of GH4720Li alloy (Q—activation energy, n and lnA—parameters independent of the temperature, which depend on strain)
本工作选用反向传递人工神经元网络(BP-ANN)技术对GH4720Li合金热变形过程中流变力学行为进行预测,人工神经元网络模型是一种基于数据驱动的模型技术[28~30],典型的人工神经元网络模型中通常包含一个输入层、一个输出层以及若干个隐含层,输入层和输出层的节点数表征所研究样本中所包含的变量个数,隐含层中每一个节点代表程序运行过程中的一个计算单元,输入信号通过逐层传递,最终由输出层实现对数据的预测[29,30]。BP神经元网络模型的运算流程如下[31]:
(1) 模型初始化,即为BP神经元网络模型的每个连接权值、阈值赋予区间[1, 1]内的随机数值;
(2) 提供输入样本x和目标输出y,并为模型设定目标精度θ;
(3) 计算实际输出,依次计算模型中隐层及输出层各单元输出:
式中,f为Sigmoid函数。
(4) 模型计算目标值与实际值的误差M:
(5) 模型修正权值:
式中,wij为模型中输入层与隐含层之间的连接权值,t为模型的训练次数,η为增益项,δpj为对于模型中j节点、p模式的误差项。其中,若j为模型中输出层节点:
若j为模型中隐含层节点:
式中,wjk为隐含层与输出层之间的连接权值;
(6) 若模型所计算隐含层单元误差M低于模型设定目标精度θ,则停止训练,否则转入步骤(2)继续执行运算,直至满足精度要求。
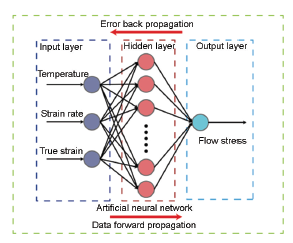
如图6所示,本工作中热变形温度、变形速率以及应变为输入层变量,流变应力为输出层变量。输入数据首先需进行归一化处理,归一化函数可表述为[32]:
式中,X为初始输入数据值,Xmax为初始输入数据中最大值,Xmin为初始输入数据中最小值。
图6 单隐含层神经元网络模型示意图
Fig.6 Schematic of the artificial neural network(ANN) architecture with one hidden layer
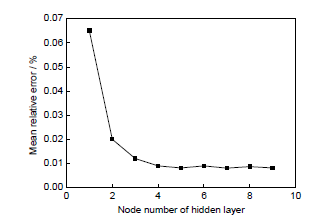
本工作中人工神经元网络模型所涉及参量为:隐含层层数为1、隐含层节点个数为5、迭代次数为2000、模型学习速率为0.03、激励函数为tansig、最小运算梯度为5.0×10-4、目标值的均方差为5.0×10-4。其中,隐含层节点个数为影响BP神经元网络模型预测精度与运算效率的关键因素,图7为本工作中BP神经元网络模型隐含层节点个数与模型预测精度之间关系曲线。可以看出,随着隐含层节点数目的增加,模型预测值的平均相对误差呈现出先减小后逐渐趋于平稳的变化趋势,当隐含层节点数目不小于5时,神经元网络模型呈现出较高的预测精度。因此,考虑模型运算效率因素,最终确定隐含层节点数为5。
图7 隐含层节点数对人工神经元网络模型预测能力的影响
Fig.7 Influence of hidden nodes on the performance of ANN
人工神经元网络模型以及包含应变参量的Arrhenius本构关系模型预测值与实验值的对比如图8所示。可以看出,包含应变参量的Arrhenius本构关系模型的预测精度较差。图9所示残差分析表明,包含应变参量的Arrhenius本构关系模型的残差在-20~60 MPa区间内分布,而人工神经元网络模型的预测结果与实验值吻合良好,残差分布区间不超过±5 MPa。采用相关系数P和平均相对误差M对包含应变参量的Ahhenius本构关系模型和BP人工神经元网络模型的预测精度进行评价,相关系数和平均相对误差可表述为[33]:
式中,Xi为流变应力实验值,Yi为流变应力预测值,为平均流变应力实验值,为平均流变应力预测值,N为所研究样本个数。
利用上式对2种本构关系模型的预测精度进行分析,得到人工神经元网络模型和包含应变参量Arrhenius本构关系模型预测结果相关系数分别为0.998和0.949,平均相对误差分别为0.814%和9.208%。上述结果表明,与包含应变参量Arrhenius本构关系模型相比,人工神经元网络模型具有更高的预测精度,因此,人工神经元网络模型更加适合用来描述本工作中GH4720Li合金热变形过程中的流变力学行为。
图8 GH4720Li合金不同热变形参数条件下流动应力实验值与理论值对比
Fig.8 Comparisons between the experimental and predicted flow curves by ANN model and Arrhenius model of GH4720Li alloy deformed at 1100 ℃ (a) and 1 s-1 (b)
图9 流动应力实验值与神经元网络模型以及Arrhenius模型残差分析
Fig.9 Comparisons of residual error between the experimental and predicted flow stress by ANN model and Arrhenius model
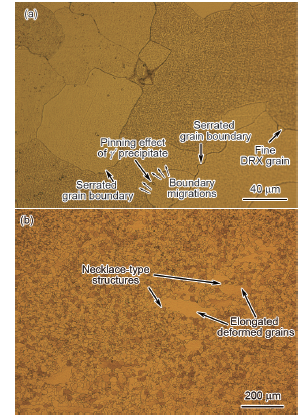
连续动态再结晶与非连续动态再结晶为镍基高温合金2种主要的动态再结晶形核机制[34],本工作采用不同变形参数条件下的热变形组织研究GH4720Li合金热变形过程中的动态再结晶形核机制。图10为变形温度1140 ℃、变形速率0.001 s-1、应变0.35和变形温度1140 ℃、变形速率1 s-1、应变0.8条件下GH4720Li合金显微组织的OM像。从图10a可以看出,在该变形参数条件下,可观察到明显的能够为动态再结晶晶粒提供形核位置的锯齿状边界,且再结晶晶粒以非连续动态再结晶的方式沿变形晶粒晶界形核。此外,还可以看出,γ'相能够对晶界起到一定的钉扎作用,从而有效地阻碍晶界的滑动和转动,大大降低了晶界迁移速率和动态再结晶晶粒长大速率。而在图10b的变形参数条件下,GH4720Li合金发生了非完全动态再结晶过程,初始形变晶粒被大量尺寸细小、均匀的等轴状动态再结晶晶粒包围,形成典型的“项链状”组织。上述分析表明,本工作中GH4720Li合金在热变形温度为1140 ℃不同应变速率条件下的动态再结晶形核方式为非连续动态再结晶。
图10 变形温度1140 ℃、变形速率0.001 s-1、应变0.35和变形温度1140 ℃、变形速率1 s-1、应变0.8条件下GH4720Li合金显微组织的OM像
Fig.10 OM images of GH4720Li alloy deformed at T=1140 ℃, =0.001 s-1, ε =0.35 (a) and T=1140 ℃, =1 s-1, ε =0.8 (b) (DRX—dynamic recrystallization)
图11为变形温度1140 ℃、应变0.8时不同应变速率条件下GH4720Li合金显微组织的OM像。可以看出,在同一热变形温度条件下,较低应变速率能够有效促进材料的动态再结晶过程,应变速率为0.001 s-1时GH4720Li合金发生了较完全的动态再结晶过程(图11a),而在应变速率为1 s-1条件下,热变形组织由细小的动态再结晶晶粒和粗大的变形晶粒组成(图11d)。上述现象主要是动态再结晶晶粒形核率和晶粒长大时间综合作用的结果,随着变形速率增加,热变形材料的变形畸变能随之升高,为动态再结晶晶粒形核提供了足够的驱动力,提高了动态再结晶形核率[35]。而在低应变速率条件下,动态再结晶晶粒比高应变速率条件下具有更充足的长大时间。
图11 变形温度1140 ℃、应变0.8时不同应变速率条件下GH4720Li合金显微组织的OM像
Fig.11 OM images of GH4720Li alloy deformed at T=1140 ℃, ε =0.8 and =0.001 s-1 (a), =0.01 s-1 (b), =0.1 s-1 (c) and =1 s-1 (d)
(1) GH4720Li合金不同热变形参数条件下真实应力-应变曲线呈现出先增加后降低,并逐渐达到稳定状态的变化趋势。且在应变速率为0.1 s-1条件下,随着温度的升高流变应力对温度的敏感性显著降低,当热变形温度由1100 ℃降低至1080 ℃,峰值应力升高23 MPa,而由1140 ℃降低至1120 ℃,峰值应力仅升高7 MPa。
(2) 通过GH4720Li合金真实应力-应变曲线分析,获得不同真应变条件下合金热变形激活能,本工作中GH4720Li合金热变形激活能不小于461.247 kJ/mol,确定了材料参数与应变之间的最佳多项式拟合阶数,建立了包含应变参量的Arrhenius本构关系模型。
(3) 对包含应变参量的Arrhenius本构关系模型和人工神经元网络模型的预测精度分析表明,Arrhenius本构关系模型的预测精度较差,平均相对误差达到9.208%,不能较好地预测材料在热变形过程中的流变力学行为,而人工神经元网络模型的平均相对误差仅为0.814%。
(4) 热变形组织分析显示,再结晶晶粒沿变形晶粒晶界形核,表明GH4720Li合金在热变形温度为1140 ℃不同应变速率条件下的再结晶晶粒形核方式为非连续动态再结晶。此外,在变形温度1140 ℃、应变0.8条件下,随应变速率的增加,动态再结晶晶粒尺寸逐渐减小,再结晶程度由完全动态再结晶向非完全动态再结晶转变。
 , 万志鹏
, 万志鹏
1 实验方法
2 实验结果及讨论
2.1 初始组织
2.2 GH4720Li合金的真应力-应变曲线

2.3 GH4720Li合金双曲正弦型Arrhenius本构关系模型


2.4 GH4720Li合金BP人工神经元网络本构关系模型


2.5 GH4720Li合金热变形组织演变规律

3 结论
来源--金属学报






 沪公网安备31011202020290号
沪公网安备31011202020290号
