分享:利用管状试样测试各向异性材料双向应力状态力学性能的新方法
摘要
为解决各向异性材料双向加载性能测试理论模型存在的测试物理量过多且实测困难的问题,提出了一种采用管状试样胀形直接测试双向加载力学性能的新方法:一点法。利用圆几何轮廓线为显性函数表达式的特征,推导了胀形过程中最高点轴向曲率半径和壁厚理论模型。仅需在胀形过程中测量最高点胀形高度,即可获得材料双向加载下的力学性能,为建立一个简单可靠且能在线实时测量的材料力学性能测试方法奠定了基础。并利用所建立的测试方法进行了AA6061铝合金挤压管坯的胀形实验。结果表明:管坯自由胀形时,其最高点实时壁厚和曲率半径均可表示为最高点胀形高度的显示函数。轮廓形状理论模型的预测精度随膨胀率的增大先提高后降低,膨胀率约为13%时预测精度最高,当膨胀率超过20%后,预测精度开始下降,但最大误差不超过±0.9%。最高点实时壁厚理论模型的预测精度基本不受试件几何尺寸的影响,长径比和径厚比改变时,差异很小,预测误差均不超过0.8%,这对保证双向加载条件下的力学性能测试精度是非常有益的。一点法可同时测得环向和轴向的应力应变分量,这为进一步分析各向异性对复杂应力状态下材料的流动及后继屈服奠定了基础。
关键词:
随着轻量化进程的发展,Mg、Al、Ti等具有明显各向异性的轻质材料在汽车、航空和航天等领域的应用越来越多[1~5],构建这些材料的本构关系模型,测试这些材料的流动应力-应变曲线,特别是双向应力状态下的力学性能,是工艺设计的重要依据。管状试样胀形是一种先进的双向应力路径力学性能测试方法[6~8],能更准确地描述复杂应力状态下材料的屈服和硬化行为,受到很多研究者的重视。但目前的理论模型存在测试物理量过多且测试困难的缺点,因此该方法目前仅处于实验室研究阶段。主要原因是采用胀形法测定材料的力学性能,需要知道整个过程中管状试样胀形高度最大处(简称为最高点)的曲率半径、壁厚以及实时内压。其中最高点壁厚和轴向曲率半径要进行实时测量非常困难,目前没有可被接受的技术手段。
目前,最高点壁厚主要是通过直接测量获得。常用的测量方法有3种:超声测厚仪测量法[9]、长臂测厚仪测量法[10~12]、将管坯剖开进行测量[13]。超声波测量法由于受管材截面弧度和内部液体介质的影响,测量精度不高。采用长臂测厚仪(类似千分尺)测量管材壁厚则需将内压卸掉才能进行测量,整个测量过程中管坯经历了多次加载卸载,这导致材料的力学性能发生了很大变化。管坯剖开测量需采用多根管状试样在不同压力下进行胀形,然后逐一测量,因无法保证多根被测试管材初始性能的一致性,测量精度同样不高。鉴于最高点壁厚难以直接测量的问题,Velasco和Boudeau[14]假设胀形过程中管坯整个轴向轮廓线内外侧均为圆弧,理论推导了最高点壁厚的解析表达式。然而采用其他学者的数值模拟与实验数据进行验证时,发现该方法所得结果精度太差,不能用于测定材料的等效应力-应变曲线。文献[15]和[16]提出了线性法,通过测量初始和最终壁厚求得管坯的力学性能,而最终壁厚如果通过超声波测厚仪测量,则如前所述不能保证最高点壁厚的准确测量;而如果剖开测量,需要实验后取出管坯,才能测量最终最高点壁厚,则不能实现应力-应变曲线的在线输出。特别是由于进行了线性假设,最终的最高点壁厚的测量精度直接影响整个过程中实时最高点壁厚的计算精度,最终降低了总体测试精度。
对于最高点轴向曲率半径,一般有2种测量方法。一种是通过测量胀形最高点附近三点的胀形高度,来拟合圆弧求最高点轴向曲率半径[9]。此方法需要3个位移传感器,实验操作困难加大,很难保证轴向曲率半径的测量精度,影响了应力-应变曲线的准确性,导致采用管状试样胀形法测试材料应力-应变曲线很难实现广泛性和标准化。另一种是对多根管坯在不同内压时胀形[13,17],然后测量每根管坯胀形区轴向轮廓线,通过函数对测量的轮廓线数据进行拟合得到轴向曲率半径。虽然对每根管坯来说测量结果较为准确,但是实验需要多根管坯,并且不能保证每根管坯初始条件的一致性。如果实验采用一根管坯,每胀一定高度,或者每到一定压力暂停实验,用三维坐标测量仪测量管坯胀形区轴向轮廓线,则实验工作量很大。所以有学者提出曲线假设法,从而避免了最高点轴向曲率半径的直接测量,其思想是将胀形区轮廓线假设为某个曲线,如余弦函数[17,18]、抛物线[19]、椭圆[10~12,20]与圆[9,14]等,通过测量胀形最高点的高度,然后拟合得到轮廓线的表达式,由曲率半径公式直接计算最高点轴向曲率半径。
由上述分析可知,要得到管坯双拉应力状态下的力学性能,需要胀形区最高点的实时壁厚和轴向曲率半径,而二者的实时大小很难直接测量,特别是实时壁厚。因此,要使管状试样胀形测试材料性能的方法具有更佳的实用性,需解决目前测量难度大和精度较低的问题。本工作采用圆弧轮廓线模型,并引入与模具相切的实际几何约束条件,基于全量理论推导了最高点实时壁厚和实时轴向曲率半径的关于胀形高度的单一变量函数表达式,这样仅需测量胀形过程中最高点胀形高度,即可求得材料的应力应变关系,本工作称为“一点法”。高度是非常便于测量的物理量,有利于保证测量精度,又提高实用性。
首先建立最高点实时壁厚和实时轴向曲率半径关于胀形高度的单一变量函数表达式。
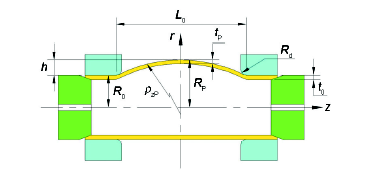
双向应力路径力学性能测试途径为将管坯放入中间为空腔的模块之间,管坯两端密封,向管坯内部打入高压液体,使管坯中间无支撑部分在内压作用下发生自由胀形。通过改变胀形区长度即可获得不同应力比状态,测试原理如图1所示。
图1 管状试样胀形实验原理及几何参数定义
Fig.1 Schematic of tube bulging test and the corresponding geometric parameters (r and z—two coordinate axes, L0—length of bulging region, t0—initial thickness of the tube, R0—initial outer radius, h—bulging height of the middle point, RP—outer radius of the middle point during bulging, tP—real-time pole thickness, ρzP—pole axial curvature radius, Rd—radius of the die)
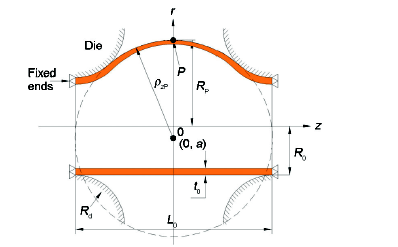
假设胀形过程中管坯轴向非贴模自由胀形区外轮廓线形状为与模具圆角相切的圆弧,如图2所示。则以坐标轴r-z为参考坐标系,记管坯初始壁厚t0,初始外半径R0,最高点胀形高度h,则胀形最高点外半径RP=R0+h,如图2所示。下面首先推导最高点轴向曲率半径ρzP和实时最高点壁厚tP与h的函数关系。
图2 轮廓线相切圆几何关系示意图
Fig.2 Die-related arc profile model for tube bulging test (P—pole point of the tube, a—ordinate of the center of the bulging region circle)
由于管坯壁厚很薄,厚度方向的应力σt与环向和轴向应力分量相比很小,近似为零。因胀形时管坯的两端固定,则根据力平衡,胀形区最高点P的轴向应力分量σz与环向应力分量σθ可分别表示为[15]:
式中,p为胀形内压,MPa;ρzP为最高点轴向曲率半径,mm;ρθP为最高点环向曲率半径,mm,ρθP=RP=R0+h。
对胀形时管坯的应变进行分析,可得到环向应变εθ与厚向应变εt分别为:
1.2.1 轴向曲率半径变化模型 因轴向轮廓线为圆弧且与模具轮廓线相切。根据几何关系,则中间胀形区轴向轮廓线可表示为:
式中,a为轮廓线圆弧对应圆心的纵坐标;rz为管材轴向轮廓线圆弧的半径,rz=RP-a。
模具轮廓线圆表示为:
式中,Rd为模具圆角半径,L0为管坯初始胀形区长度。
由于模具轮廓线和中间胀形区轮廓线两圆相切,联立式(3)和(4),消去z得到关于r的一元二次方程,进一步根据两圆相切的条件Δ=0 (Δ为二次函数根的判别式)计算可得:
则中间胀形区圆弧表示为:
根据圆的轴向曲率半径计算公式ρzP=rz,联立式(6)计算得到:
由式(7)可见,ρzP仅与胀形过程中变量h有关,即只需在胀形过程中得到实时的h就可以计算得到ρzP。
1.2.2 最高点壁厚变化模型 由于自由胀形为简单变形,最高点的应力应变主轴保持不变,则应变分量与应力偏量之间的关系为:
式中,εθ为环向应变分量,εz为轴向应变分量,σ′z为轴向应力偏量,σ′θ为环向应力偏量。
将式(2)代入上式,可得:
由于管坯壁厚相对于环向和轴向曲率半径很小,可以忽略,式(1)轴向与环向应力可进一步整理为:
假设最高点轴向与环向曲率半径比值为α,则ρzP可以表示为:
将式(12)代入式(10)中σθ表达式,环向应力即可表示为管坯初始条件和α的函数式:
将式(10)代入式(13)得环向与轴向应力偏量的比值为:
将式(9)和式(14)代入式(8),并整理成tP的表达式:
将式(7)、(15)代入式(1),可得仅含p和h 2个变量的应力分量表达式:
式中,β =(4h2-24hRd-8hR0+
同理,将式(7)、(15)代入式(2),可得仅含变量h的应变分量表达式:
由式(7)、(15)可以看出,将管坯两端固定进行胀形时,其ρzP和tP均为h的函数式,则根据式(16)和(17),最高点的各应力应变分量均可表示为h的显式函数。这样只需在胀形过程中得到实时的h,即可建立薄壁管的等效应力-等效应变本构关系。实验计算原理流程图如图3所示。这克服了管坯胀形性能测试存在的轴向曲率半径和最高点壁厚无法实时测量的难题,解决了管状试样力学性能的在线实时测量的问题。
图3 一点法测试材料流动应力-应变曲线的理论算法流程图
Fig.3 Flow chart for testing flow stress-strain curve on line based on one point method
为验证上述理论模型的合理性和准确性,采用AA6061挤压铝合金管材进行了胀形实验。管材初始外径为50 mm,壁厚为1.8 mm。模具约束圆角半径为15 mm。长径比λ分别为1.4和1.8。对于每一个长径比,均取3根管材分别胀形到不同高度,然后测量每根管坯对应的胀形区轮廓线。AA6061铝合金胀形后管材照片如图4所示。对于图4a所示管坯,对应的胀形高度从左至右依次为1.5、3.5和5.3 mm;对于图4b所示管坯,对应的胀形高度从左至右依次为1.1、3.1和5.1 mm。
图4 不同长径比AA6061铝合金管材胀形后照片
Fig.4 Photos of AA6061 aluminum tubes after bul-ging test with ratios of length-to-diameter λ=1.4 (a) and λ=1.8 (b)
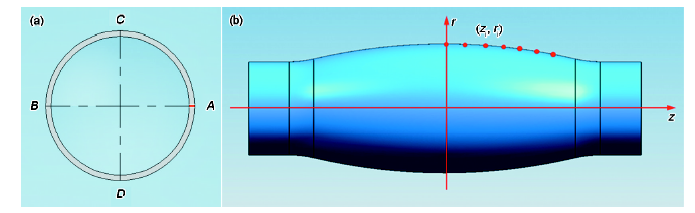
由于管坯沿环向初始壁厚存在不均匀性,尤其对于变形的后期阶段,管坯沿轴向呈轴对称变形,因此实验前测量每根管坯环向初始壁厚分布,最小壁厚点记为A,如图5a所示。实验结束后,所有管坯沿过CD的截面切开,然后如图5b所示测量胀形区轮廓线。
图5 胀形管材轮廓线测量示意图
Fig.5 Axial contour measuring of tested tubes(a) hoop cross section (b) schematic of contour measuring
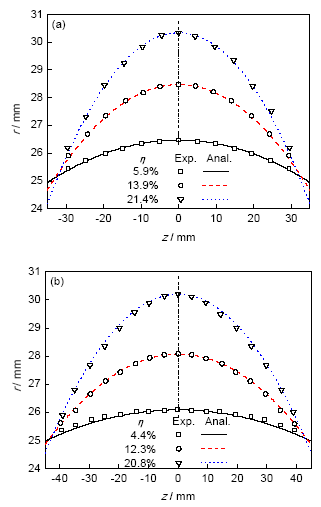
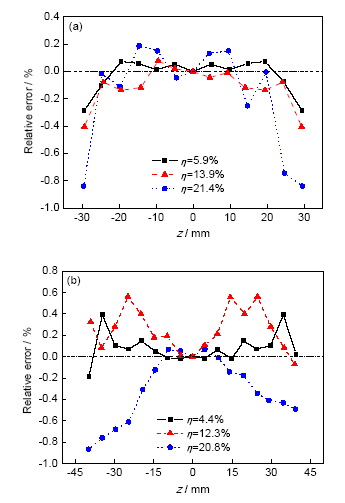
图6为实验测量及理论分析所得的不同长径比AA6061铝合金胀形后管坯轮廓线。图中η表示管坯膨胀率,η=h/R0100%。由图可见,理论分析结果与实验结果吻合很好。为更清晰地揭示理论分析结果的可靠性,对2组长径比试件进行误差分析,如图7所示。可以看出,随着胀形进行误差逐渐减小,但当膨胀率超过20%后,理论预测值反而开始降低小于实验值,预测误差开始增大,但理论结果最大误差小于±0.9%,说明采用相切圆模型计算ρzP是可靠的。
图6 实验测量及理论分析所得的不同长径比AA6061 铝合金管材胀形后管坯轮廓线
Fig.6 Axial contour of AA6061 aluminum tubes after bulging test obtained by experiments and theoretical analysis with λ=1.4 (a) and λ=1.8 (b) (η—tube expansion, η=h/R0100%)
图7 不同长径比AA6061 铝合金管材胀形过程中轮廓线相切圆模型误差分析
Fig.7 Error analyses of tangency circle geometric model to fit the axial contour of AA6061 aluminum tubes in bulging test with λ=1.4 (a) and λ=1.8 (b)
为了验证壁厚理论计算模型的合理性,进行了相应的管材胀形实验。为验证理论模型的普适性,对比了不同长径比和厚径比试件,具体实验方案如表1所示。实验材料为AA6061铝合金挤压管材,对于各种类型的管材均选取多种不同胀形区长度进行胀形实验。
表1 AA6061管材胀形实验方案
Table 1 Experimental schemes for tube bulging tests of AA6061 tubes
实验前标记管材胀形区中间点(也就是胀形最高点),在胀形过程中,通过超声波测厚仪连续测量不同压力阶段对应的胀形区最高点壁厚,直至管材破裂(超声波测厚仪为DAKOTA PX-7,测量精度为0.001 mm)。
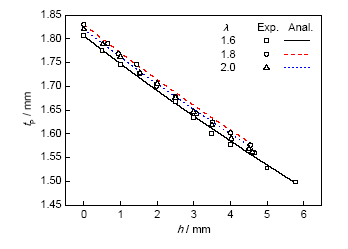
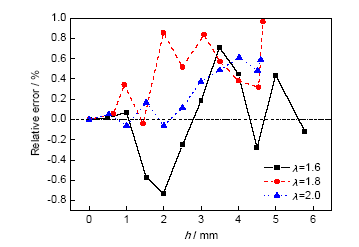
2.2.1 最高点壁厚变化模型 不同长径比胀形时最高点壁厚的实验结果如图8所示。对应的误差分析如图9所示。管材初始外径60 mm,初始壁厚为1.8 mm,模具圆角半径为15 mm。可见,最高点壁厚理论模型计算结果与实验结果吻合很好,最大误差不超过±1%。不同胀形区长度时最高点壁厚随胀形高度的变化关系非常接近,这表明最高点壁厚随胀形高度的变化规律对胀形区长度不敏感。考虑到胀形区长度与最高点的应力状态是一一对应的,这说明该理论模型预测精度不受应力状态的影响,这对保证双向加载条件下的力学性能测试精度是非常重要的。
图8 不同长径比时最高点壁厚与胀形高度的实验结果
Fig.8 Experimental results of pole thickness and bulging height with different length-to-diameter ratios under D0=60 mm and t0=1.8 mm
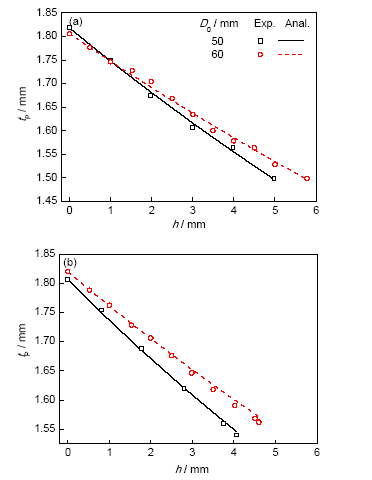
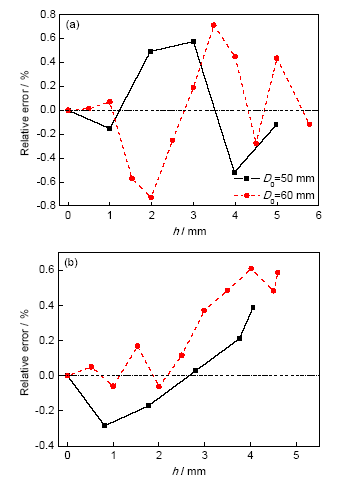
2.2.2 径厚比的影响 对初始壁厚均为1.8 mm,长径比1.6和2.0,初始外径分别为50和60 mm的管材进行胀形实验。得到不同管径胀形时的最高点壁厚与胀形高度实验结果如图10所示。可以看到,对于不同初始壁厚及长径比的管材,理论模型计算结果均与实验结果吻合很好。只是对于不同初始外径的管材,最高点壁厚随胀形高度变化速率不同。初始外径越小,随胀形高度的增加最高点壁厚减小得越快。需要指出的是,理论模型预测精度并没有降低,如图11所示,最大误差均不超过±0.8%。
图9 不同长径比时最高点壁厚与胀形高度的误差分析
Fig.9 Error analyses of pole thickness and bulging height with different length-to-diameter ratios under D0=60 mm and t0=1.8 mm
图10 不同初始外径时最高点壁厚与胀形高度的实验结果
Fig.10 Experimental results of pole thickness and bulging height with different initial outer diameters under t0=1.8 mm and λ=1.6 (a), λ=2.0 (b)
图11 不同初始外径时最高点壁厚与胀形高度的误差分析
Fig.11 Error analyses of pole thickness and bulging height with different initial outer diameters under t0=1.8 mm and λ=1.6 (a), λ=2.0 (b)
利用所建立实验方法进行了AA6061铝合金挤压管材的胀形实验,并通过KEYENCE IL065激光位移传感器(测量精度为0.01 mm)连续在线测量此处的胀形高度。通过WIKA, S-10压力传感器(测量范围为0~60 MPa,测量精度为0.15 MPa)连续测量胀形内压。管材的具体尺寸如表1所示。由于本工作所采用的铝合金管材均是通过一种加工工艺制作,所以仅对初始壁厚1.8 mm,外径60 mm,长径比1.6的管材进行了测试。
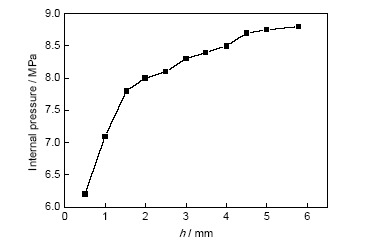
图12 胀形高度随胀形内压的变化关系曲线
Fig.12 Bulging height at the middle point variation with the internal pressure (D0=60 mm, t0=1.8 mm, λ=1.6)
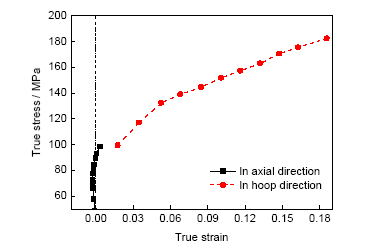
图12所示为通过位移传感器测得的最高点位移与内压的关系曲线,根据式(16)和(17)得到的应力-应变分量如图13所示。可见,一点法仅通过位移传感器和压力传感器即可测得整个胀形过程中的环向和轴向应力应变分量。由图13还可以看出,管材胀形时最高点既不是简单的平面应力状态(轴向应力约等于环向应力的1/2),更不同于单拉应力状态,这同样说明进行管材性能测试方法研究的必要性。
图13 流动应力-应变分量曲线
Fig.13 Flow stress-strain curve (D0=60 mm, t0=1.8 mm,λ=1.6)
应用Mises各向同性屈服准则以及塑性变形体积不变条件,管材自由胀形时最高点处等效应力σi和等效应变εi可以表示为:
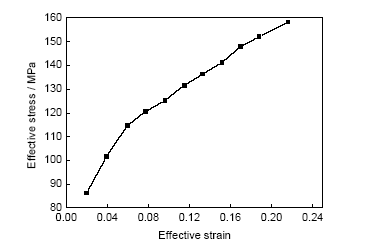
由式(18)得到的等效应力-应变曲线如图14所示。该曲线可用于有限元分析或成形极限分析。但由图13可知,该测试方法同时测得了各应力-应变分量,当采用文献[21~24]中的各向异性屈服准则时,则可得到受各向异性影响的等效应力-应变曲线,这对管材性能测试来讲是十分重要的,因为无论是无缝管还是焊管,其各向异性特征均非常明显[25]。该测试方法为进一步研究各向异性对复杂应力状态下材料的流动及后继屈服奠定了基础。
图14 AA6061铝合金管材等效应力-应变曲线
Fig.14 Equivalent stress- strain curves of AA6061 tubes (D0=60 mm, t0=1.8 mm, λ=1.6)
(1) 提出了基于最高点胀形高度测试管材力学性能的新方法:一点法。两端固定管材自由胀形时,其最高点实时壁厚和曲率半径均可表示为最高点胀形高度的显示函数,因此只需测得胀形过程中的实时胀形高度,即可获得薄壁管双向加载下的力学性能。
(2) 轮廓形状的理论模型预测精度受膨胀率影响,其预测精度随膨胀率的增大先升高后降低,膨胀率约为13%时预测精度最高,当膨胀率超过20%后,预测精度开始下降,但最大误差不超过0.9%。
(3) 长径比和径厚比改变时,最高点实时壁厚理论模型的预测精度差异很小,预测误差小于0.8%,这说明该理论模型的预测精度对试件几何尺寸不敏感,这对保证双向加载条件下的力学性能测试精度是非常有益的。
(4) 一点法可同时测得环向和轴向的应力应变分量,为准确描述各向异性特征明显的管材的塑性变形特征奠定了基础。
1 管状试样双向加载力学性能直接测试理论模型
1.1 测试原理
1.2 轴向曲率半径及最高点壁厚变化模型
1.3 应力应变数学模型

2 理论模型的实验验证
2.1 相切圆几何模型的实验验证

2.2 最高点壁厚理论模型的实验验证
λ=L0/D0
δ=D0/t0
D0 / mm
L0 / mm
t0 / mm
1.6
27.8
50
80
1.8
2.0
27.8
50
100
1.8
1.6
33.3
60
96
1.8
1.8
33.3
60
108
1.8
2.0
33.3
60
120
1.8
3 AA6061铝合金管坯应力-应变曲线
4 结论
来源--金属学报







 沪公网安备31011202020290号
沪公网安备31011202020290号
