陈瑞1, 许庆彦1,  , 郭会廷2, 夏志远2, 吴勤芳2, 柳百成1
, 郭会廷2, 夏志远2, 吴勤芳2, 柳百成1
1 清华大学材料学院先进成形制造教育部重点实验室 北京 100084
2 明志科技有限公司 苏州 215006
摘要
建立了时效析出动力学模型、强化模型以及应变硬化模型,针对Al-7Si-Mg合金开展拉伸性能模拟研究。时效析出动力学模型可以模拟析出相密度、尺寸、分布、体积分数、基体中元素含量等微观组织参数,并结合强化模型获得合金的屈服强度。通过应变硬化模型可模拟合金在拉伸过程的应力-应变曲线,并结合关系式(σUTS-σY)=mσY+n+f (Tss)获得合金的抗拉强度和延伸率。本工作首先模拟了Al-7Si-0.4Mg合金的析出相特征参数及屈服强度并进行实验验证,分析了模拟结果与实验结果之间存在偏差的可能原因。采用应变硬化模型模拟了Al-7Si-0.36Mg合金在拉伸过程的应力-应变曲线,分析时效处理和铸态组织细化程度对位错存储速率、动态回复速率及合金的应力-应变曲线的影响规律。采用本模型预测了Al-7Si-0.4Mg合金在不同时效温度下的抗拉强度和延伸率,并与实验结果进行对比,分析了二次枝晶臂间距对拉伸性能的影响。最后,对模型存在的局限性及影响拉伸性能预测精度的因素进行了分析。
关键词: Al-7Si-Mg铝合金 ; 拉伸性能 ; 应变硬化 ; 析出相 ; 时效处理 ; 模拟
Al-7Si-Mg (质量分数,%)合金,如ZL114、A356、A357,属于典型的Al-Si系铸造铝合金,因其具有较好的流动性,可以成型大型薄壁复杂铸件,同时可通过热处理析出Mg-Si强化相,从而实现时效强化,该合金具有轻质、高强、易成型等一系列优点,是汽车缸体、缸盖、变速器壳体、轮毂等重要零部件的典型材料[1,2]。对Al-7Si-Mg铝合金铸件力学性能方面的要求,主要包括拉伸过程的屈服强度、抗拉强度和延伸率。Al-7Si-Mg铝合金铸件的力学性能由凝固和热处理过程中形成的微观组织所决定,因此,建立工艺参数与微观组织之间的定量化模型,并结合相应的强化模型来研究工艺参数对铸件力学性能的影响规律,对于优化工艺条件,提高铸件质量具有重要的工程应用价值。
Al-7Si-Mg铝合金铸造过程中涉及凝固、固溶、淬火、时效等工序,每一加工工序都会影响铸件的最终力学性能。凝固过程形成的枝晶和共晶组织以及缺陷组织都会影响后续的拉伸性能,枝晶组织越细,形成的共晶相和缺陷组织尺寸越小,合金的力学性能越好,特别是能明显改善合金的抗拉强度和延伸率[3,4]。固溶处理和淬火处理主要是为了改善Al-7Si-Mg合金的共晶硅组织形貌,溶解含Fe金属间化合物,并形成过饱和固溶体[5]。时效处理是影响Al-7Si-Mg合金拉伸性能的最主要工序,该过程形成的析出相可极大提高合金的强度,但会使其延伸率降低。目前采用时效析出动力学模型来模拟时效过程中析出相的演变是研究热点之一。基于KWN(Kampmann-Wagner)模型思想的解析模型是最常用的时效析出动力学模型,它涉及析出相的形核、生长和粗化过程,可以得到析出相密度、尺寸、体积分数等宏观参数,易与现有的强化模型相关联,实现屈服强度的预测[6~8]。目前,大部分的时效析出动力学模拟以及屈服强度预测工作主要针对Al-Mg-Si及Al-Cu等合金,对于Al-Si-Mg铸造铝合金,由于其最终力学性能除了受析出相影响之外,还与枝晶、共晶等凝固组织密切相关,目前针对该合金的相关研究鲜有报道。
材料的抗拉强度和延伸率与材料在拉伸过程中的应变硬化行为有关,而应变硬化行为通常用应力-应变曲线来进行定量评价。目前有一些基于经验性的应变硬化模型,可描述材料在塑性变形阶段的应力-应变曲线,如Hollomon模型[9]、Ludwigson模型[10]、Voce模型[11]等,广泛应用于研究材料的微观结构和变形机制之间的联系(尤其是在单向拉伸和压缩条件下)。此外,应用这些模型的参数化分析,可对材料的成形性能进行评价。基于塑性变形过程中位错密度的变化对材料硬化行为的影响,Kocks-Mecking-Estrin (KME)提出的应变硬化理论已广泛应用于研究金属的应变硬化行为。KME模型最初主要应用于纯金属的应力-应变曲线模拟。对于合金材料,由于溶质原子或析出相的存在,KME模型需要进行相应修正。因为溶质原子会改变堆垛层错能并引起溶质拖曳效应(solute drag effect),降低动态回复速率[12],而析出相的存在会成为位错钉扎和集聚的地方,所以两者都会使位错密度增加,提高合金的硬化能力。目前,很多学者基于KME模型开展了变形铝合金应变硬化行为的模拟研究[13~17]。Cheng等[12]采用KME模型,研究了时效析出对AA6111合金应力-应变曲线的影响,结果表明材料的硬化速率受应力叠加方式及位错与析出相之间的作用机制的影响。Bardel等[17]基于KME理论建立了应变硬化模型,考虑了晶界和析出相对随动硬化和各向同性硬化的影响,并结合之前建立的时效析出模型和屈服强度模型,研究了6061铝合金在周期应力条件下的变形行为。材料的抗拉强度和延伸率还与其断裂行为相关。由于Al-7Si-Mg合金在拉伸过程的断裂很大程度上受材料内部的缺陷组织、含铁金属间化合物以及共晶硅颗粒的影响,目前还没有相应的定量化模型用于预测该合金的抗拉强度和延伸率。实验研究[18,19]表明,对于Al-7Si-Mg合金,材料的拉伸性能之间满足一定的经验性关系式。因此可以结合拉伸性能之间的经验性公式以及应变硬化模型来模拟材料的抗拉强度和延伸率。
本工作主要针对Al-7Si-Mg铸造铝合金建立时效析出动力学模型、强化模型以及应变硬化模型,并基于实验数据获得抗拉强度和屈服强度之间的关系式,开展应力-应变曲线的模拟以及相应拉伸性能的预测。同时开展相关的实验研究,对模拟结果进行验证,分析时效工艺参数和组织细化程度对拉伸性能的影响规律。
1 模型描述
Al-7Si-Mg合金铸件的力学性能指标主要包括拉伸过程的屈服强度σY、抗拉强度σUTS和延伸率e,本工作中的延伸率为均匀延伸率,即抗拉强度对应处的变形量。Al-7Si-Mg合金的工程应力-工程应变曲线(σ-ε)示意图如图1a所示,合金在拉伸过程的硬化速率分为2个阶段,如图1b所示。在低应变阶段,合金的硬化速率θ随应力σ的增大呈非线性减小,在高应变阶段,θ随σ的变化遵循线性关系,通常可表示为:
(1)
式中,θ0为初始硬化速率,K为反映材料动态回复速率大小的无量纲参数[20],等于dθ/dσ。
图1 Al-7Si-Mg合金拉伸过程工程应力-工程应变曲线及硬化速率随应力变化示意图
Fig.1 Schematics of the engineering stress-engineering strain curve (σ-ε) during tensile process
(a) and the change of strain hardening rate (θ) with stress (b) of Al-7Si-Mg aluminum alloy (σY and σUTS—yield strength and ultimate tensile strength, respectively; e—elongation; εY—engineering strain corresponding to the yield strength; θ0—initial strain hardening rate)
1.1 时效析出动力学模型
Al-7Si-Mg合金在热处理过程析出细小弥散的析出相,是引起其强度大幅提升的主要原因,其强化效果由析出相的形貌、密度、尺寸及分布等因素决定。本文作者在前期工作[21]中,基于经典的形核生长理论,建立了相关的时效析出动力学模型,其中析出相的形核速率dN/dt与生长速率v的表达式为:
(2)
(3)
式中,N0为单位体积固溶体中有效形核质点数;Z和β*分别为Zeldovich因子和原子往核心上的堆垛速率;?G*为临界形核活化能;kB为Boltzmann常数;T表示时效温度; 表示形核孕育时间,其中τ=2/(πβ*Z2)[22],t为时效时间;rp为析出相半径;?为长径比(?=lp/2rp,lp为析出相长度); 是溶质元素在基体中的扩散矩阵;ξ是有效扩散长度调整因子[23]; 、 、 分别表示组元j在基体中的平均摩尔分数、Gibbs-Thomson效应引起的析出相/基体界面处组元j的局部平衡溶质成分、组元j在析出相中的平均摩尔分数; ,其中 、 分别为基体和析出相的摩尔体积。详细模型和推导参见文献[21]。
1.2 屈服强度模型
决定Al-7Si-Mg合金屈服强度的因素,主要包括铝基体的本征强化(?σi)、共晶硅颗粒强化(?σeutectic)、晶界强化(?σGB)、溶质原子固溶强化(?σss)以及Mg-Si第二相的析出强化(?σppt)。假设上述几种因素可以线性叠加,则该合金的屈服强度σY可表示为:
(4)
式中,?σGB由晶粒度和二次枝晶臂间距(d)决定,而?σeutectic由共晶Si颗粒的尺寸、密度、形貌等因素决定。考虑到?σi、?σeutectic、?σGB这3项在时效过程不发生变化,因此可用?σ0来表示,则σY表示为:
(5)
需要指出的是,?σ0的大小取决于凝固和固溶处理条件。
基体中析出相一般存在2种析出强化机制,分别是位错切过机制(rp≤ )和位错绕过机制(rp> ), 为临界半径。本模型对于切过和绕过机制的切应力 和 分别进行计算:
(6)
式中,Nk(rp)和 分别为第k分组的析出相密度和强度,Γ为位错线张力,b为Burgers矢量模,G为铝基体的剪切模量,δ是个与位错线的特征和形状有关[24]的常数。根据Ardell[25]提出的强化效应叠加原则,并且把切应力转化为正应力,就可得到析出强化效果Δσppt= ,式中,M为Taylor因子,q为指数,在1~2之间。
1.3 应变硬化模型
当达到屈服强度以后,合金受到的应力随着塑性变形量的增大继续增大,会发生应变硬化。在该过程中主要有2方面硬化因素[16,26]:一是基体中位错密度ρ的变化所引起的各向同性硬化Δσiso (isotropic strain hardening),另一方面是由于位错塞积在析出相、晶界、共晶硅周围,阻碍其进一步推移而产生的随动硬化Δσkin (kinematic strain hardening)。本模型采用线性叠加的方式获得拉伸过程真应力σT的表达式:
(7)
式中,σY_T表示屈服强度对应处的真应力。根据真应力-真应变(σT-εT)和工程应力-工程应变(σ-ε)之间的转换关系σT=σ(1+ε)/(1-ε),εT=ln(1+ε)[27],式(7)可转化为:
(8)
式中,ε=exp(εT)-1=exp(ε_T+εY_T)-1,ε_T表示材料屈服后所发生的真应变量,εY_T表示屈服强度对应处的真应变量(包括弹性变形和0.2%残余变形)。根据Hooke线弹性准则[17],屈服强度可表示为:
(9)
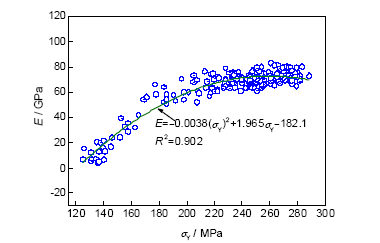
式中,εY-0.2表示在达到屈服之前发生的弹性变形量,E为材料的Young's模量。式(9)中的屈服强度可由式(5)获得,因此若知道材料的E,就可以获得εY。图2是由实验数据获得的Al-7Si-Mg合金在不同屈服强度下的Young's模量。图2表明,E与σY之间的关系可用二次多项式来表示。
图2 Al-7Si-Mg合金的Young's模量随屈服强度的变化曲线
Fig.2 Curve of Young's modulus of Al-7Si-Mg alloy vs yield strength (E—Young's modulus, R2—standard deviation)
各向同性硬化效果由基体中的位错林(forest discolation)密度ρs和位错环(dislocation loop)密度ρp决定,其硬化效果可表示为[13]:
(10)
式中,α是常数,取值0.3[12]。随动硬化产生的原因是尺寸大于 的析出相阻碍位错的滑移,而在其周围产生应力场。对于球形析出相,析出相周围位错环所引起的未释放剪切塑性变形量(unrelaxed shear plastic strain)为 ,其中,np为析出相周围的位错环数目,rp_by为尺寸大于 的析出相的平均半径[28]。对于Al-7Si-Mg合金中沿[001]Al方向析出的针状析出相, 的表达式为:
(11)
式中,lp_by表示尺寸大于 的析出相的平均长度。随着应力的增大,析出相周围的位错环会变得不稳定,从而会切过析出相并发生湮灭。因此,在式(11)中引入0~1之间的参数φ,用于表示位错环在析出相周围的稳定程度。φ的表达式如下所示[29]:
(12)
式中,rcl表示析出相与基体非共格时的半径[29]。当rp≤ ,位错可以切过析出相而继续推移,因此在析出相周围不会形成位错环;当 <rp<rcl时,析出相周围形成的位错环随着应力的增加,会变得不稳定从而切过析出相并发生湮灭;当rp≥rcl时,析出相尺寸较大且与基体非共格,形成的位错环是稳定的。结合Eshelby模型[28],析出相周围位错环所引起的随动硬化效果Δσkin_p可表示为:
(13)
式中,Ep为析出相的Young's模量,fv_by表示尺寸大于 的析出相的体积分数。从式(13)中可看到,析出相引起的随动硬化效果,由尺寸大于 的析出相的体积分数、平均尺寸以及周围位错环数目所决定。
随着塑性变形的进行,析出相周围累积的位错环数目并不会无限制地增加,因为当析出相受到的内部压力足够大时,会使析出相发生断裂,从而形成新的自由表面,使得位错环发生湮灭,或是析出相表面受到的应力会触发动态回复机制阻碍位错环的进一步堆积[28],所以析出相周围的位错环数目存在上限值 。基于Proudhon等[28]针对球形析出相建立的位错环存储速率表达式 ,本工作针对针状析出相进行修正,并表示如下:
(14)
式中,引入 修正项主要是避免np无限增大。从式(14)可以看到,np的变化与析出相尺寸以及塑性变形量相关。对式(14)进行积分,得到np的表达式如下:
(15)
除了析出相对随动硬化有贡献之外,在晶界及晶界处的共晶硅颗粒周围,由于位错的塞积一方面增加了基体中位错林密度,从而产生各向同性硬化效果(该因素包含在Δσiso中),另一方面会产生背应力,引起随动硬化效果Δσkin_e。本工作借鉴Sinclair等[30] (用于求解晶界所引起的随动硬化效果)的模型,提出了计算Al-7Si-Mg合金中晶界和共晶硅颗粒所引起的随动硬化效果模型Δσkin_e:
(16)
(17)
式中,Nn为塞积在晶界和共晶硅颗粒周围某一滑移带上的位错数目,N*为位错塞积的临界数目,λ为剪切带上滑移线之间的平均间距。在Sinclair等[30]研究中,D表示晶粒尺寸,而在本模型中,D是一个综合了枝晶细化程度和共晶硅颗粒尺寸的参数。结合式(12, 13, 15, 16, 17)就可以得到不同应变量下的随动硬化效果Δσkin。
1.4 位错密度计算
对于析出相密度为Nk (rp)的第k分组析出相(尺寸rp> ),其单个析出相周围存储的位错环数目为φnp,单个位错环长度为2πrp,则基体中形成的位错环密度ρp可表示为[16]:
(18)
材料在塑性变形过程中,基体中位错林密度ρs的变化取决于位错存储和位错湮灭2个动态过程,ρs随应变量的变化可表示为:
(19)
式中第一项表示位错的塞积使ρs增大,第二项表示动态回复使ρs减小。式(19)一般可用KME模型进行描述:
(20)
式中,k1是与位错存储速率相关的参数;k2是与动态回复速率有关的参数,与位错间的临界湮灭距离y有关,k2=2y/b。基体中析出相的存在,除了形成位错环之外,还会影响动态回复速率。研究[16]表明,析出相周围应力场的增大,会提高堆垛层错能,促进析出相附近位错的交滑移发生,进而增加位错间的临界湮灭距离,加快材料的动态回复速率。本工作采用Fribourg等[16]提出的动态回复速率表达式:
(21)
式中, 和 是与动态回复速率相关的参数,其中 与位错环有关。该方程右边第一项表示不考虑位错环影响时基体中正负位错相互湮灭对k2的贡献,右边第二项表示析出相周围位错环的作用所引起的正负位错间相互湮灭对k2的贡献。需要说明的是,除析出相周围形成的位错环之外,基体中溶质原子含量变化也会影响材料的动态回复速率,一般k2随着溶质元素含量的减小而增大[31]。通过式(12, 15, 18)可以计算得到不同应变量下的基体中位错环密度,通过式(12, 20, 21)可以得到位错林密度,代入式(10)后,可以获得各向同性硬化效果Δσiso。
2 实验研究
2.1 实验方案
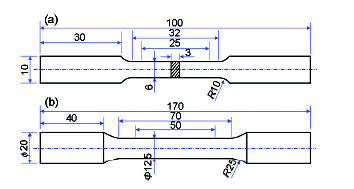
本工作主要采用2种拉伸试样来进行力学性能测试,一种是采用砂型铸造方式浇注的标准尺寸拉伸试棒,棒中二次枝晶臂间距为45.2 μm,成分为Al-7Si-0.4Mg (质量分数,%)合金,用于验证拉伸性能预测结果。另一种是从阶梯件(参见文献[32])上获取的片状试样,成分为Al-7Si-0.36Mg合金,用于研究拉伸过程的应变硬化行为。2种拉伸试样的几何尺寸如图3所示。由于阶梯件每个阶梯部位的凝固组织细化程度不一样,二次枝晶臂间距d在70.1~24.9 μm之间变化,因此可以获得具有不同程度塑性变形能力的拉伸实验结果。2种合金的熔炼温度为720~740 ℃,经过Ar气除气处理、Al-5Ti-1B细化处理以及Al-10Sr变质处理。2种拉伸试样经过相应的固溶、70 ℃热水淬火以及人工时效热处理(T6),具体的热处理工艺见表1。热处理后试样的析出相组织观察在Tecnai G2 F20场发射透射电子显微镜(TEM)上进行,加速电压为200 kV。TEM观察前样品首先采用机械减薄后进行电解双喷减薄(电解液为25%HNO3+75%CH3OH (体积分数)的混合液),电压20 V,温度-30 ℃。双喷减薄后的试样再进行离子减薄,电压4 kV,电流0.01 A,时间5~10 min。拉伸性能测试在AG-IC100KN拉伸试验机上进行,拉伸速率1 mm/min,记录拉伸过程的工程应力-工程应变曲线,从而获得每一热处理条件下试样的σY、σUTS、e以及E。
图3 片状和棒状拉伸试样的几何尺寸
Fig.3 Dimensions of flat shape (a) and cylindrical shape (b) tensile samples (unit: mm)
2.2 实验结果
2.2.1 析出相组织演变 图4所示为Al-7Si-0.4Mg合金在180 ℃时效不同时间后的TEM像。由图可见,时效20 min后的试样中(图4a),基体中主要包含溶质原子的偏聚形成的GP区,直径为2~4 nm。由于GP区富含Si和Mg原子,引起基体晶格畸变,所以在HRTEM照片上能看到明显的应变场衬度(图4d)。从图4d也可以看到,基体中除了GP区外,也存在少量晶胞为单斜结构的析出相,尺寸大概在2~3 nm,通过测定晶格参数和晶体取向可以判断该相是β"相。时效4 h后,基体中出现了大量沿着Al基体[001]方向生长的针状析出相,其中黑色点状物为针状析出相的端面[33]。从图4e可看到,针状析出相的轴向截面与基体完全共格,从端面的高分辨照片可判断其为单斜结构相,因此可知该相为β"相。时效120 h后(图4c),基体中的β"相密度降低,同时也出现了棒状的β'相和块状Si相,其中β'相与基体呈现半共格(图4f)。表2是针状β"析出相的平均半径和长径比随时效温度和时间的变化。可以看到,随着时效时间的延长,析出相尺寸增大,当时效温度提高时,由于析出相生长速率增大,在较短时间内即可达到较低温度下时效较长时间的析出相尺寸。根据180 ℃时效的数据可以看到,析出相长径比随着时效时间的延长先增大后减小,这与其它文献报道的结论相一致[34]。此外,β"相长径比随时效工艺的变化基本在6~9范围内波动。
图4 Al-7Si-0.4Mg合金在180 ℃时效不同时间后的TEM和HRTEM像
Fig.4 TEM (a~c) and HRTEM (d~f) images of Al-7Si-0.4Mg alloy artificially aged at 180 ℃ for 20 min (a, d), 4 h (b, e) and 120 h (c, f) (Insets in Figs.4d and e show the cross section of needle-shaped precipitates)
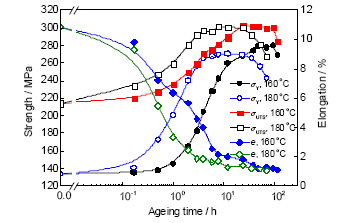
2.2.2 拉伸性能分析 图5为160和180 ℃时效条件下,合金的拉伸性能随时效时间的变化结果。180 ℃时效条件下,在时效时间0~4 h之内,随着时效时间的延长,合金屈服强度和抗拉强度快速增加,而延伸率急剧减小,抗拉强度和屈服强度之间的差值(σUTS-σY)逐渐减小。在时效时间4~24 h区间,合金的强度变化不明显,延伸率缓慢下降,并且σUTS-σY变化也很小。当时效时间超过24 h,合金进入过时效阶段,合金的强度开始降低,延伸率变化不大,而σUTS-σY逐渐减小。比较2组时效温度下的拉伸性能可知,时效温度的升高会使合金达到时效峰值的时间急剧缩短。
图5 Al-7Si-0.4Mg合金在160和180 ℃下随时效时间的拉伸性能
Fig.5 Tensile properties of Al-7Si-0.4Mg alloy as a function of ageing time at 160 and 180 ℃
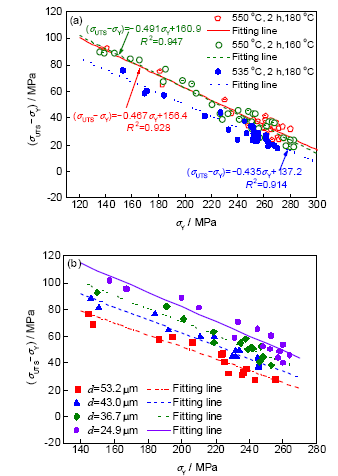
材料的屈服强度和抗拉强度之间存在一定的对应关系,本工作首先归纳出Al-7Si-Mg合金中(σUTS-σY)和σY之间的关系式,以获得合金的抗拉强度。需要说明的是,本工作主要针对欠时效和峰时效的拉伸性能数据进行分析,主要原因有3个:(1) 过时效阶段(σUTS-σY)和σY之间的变化规律与欠时效和峰时效阶段的不相同;(2) 实际应用的Al-7Si-Mg合金铸件基本都是欠时效和峰时效状态;(3) 本模型计算的屈服强度在过时效阶段误差较大。图6a为Al-7Si-0.4Mg合金在不同热处理条件下的(σUTS-σY)随σY的变化规律。可以看出,(σUTS-σY)随着σY增大呈线性减小,并且当σY处于230~280 MPa之间时,(σUTS-σY)数据波动幅度较大。从160和180 ℃条件下的拟合结果可以看到,时效温度对(σUTS-σY)和σY之间的关系影响很小,而固溶温度的降低则会明显降低(σUTS-σY),这主要是因为固溶温度降低,会减慢共晶硅颗粒的熔断和球化,同时也会使含Fe金属间化合物溶解不完全,从而导致合金的抗拉强度和延伸率降低。除了热处理条件之外,铸态组织如凝固过程形成的缺陷、枝晶细化程度、共晶硅形貌和尺寸等,也是影响Al-7Si-Mg合金断裂的重要因素。二次枝晶臂间距是用于评价Al-7Si-Mg合金铸态组织细化程度的重要指标,本工作分析了含有不同二次枝晶臂间距的片状拉伸试样在经过550 ℃固溶2 h,180 ℃条件下时效不同时间后(σUTS-σY)随σY的变化规律,结果如图6b所示。可以看到,(σUTS-σY)随着二次枝晶臂间距d的减小逐渐增大,并且(σUTS-σY)和σY之间满足如下表达式:
(22)
式中,m=0.00342d-0.6275,n=-1.744d+234.4,由图6b中的实验结果拟合得到。同时为了反映不同固溶处理温度Tss对(σUTS-σY)的影响,在公式(22)中添加了f(Tss)项,f(Tss)=(-0.03σY+19.2)[(Tss-550)/15]。该方程右边第一项为图6a中550和535 ℃ 2组固溶温度下的(σUTS-σY)拟合曲线的差值。可以看出,当Tss=550 ℃时,f(Tss)=0;当Tss=535 ℃时,f(Tss)=-(-0.03σY+19.2)。基于公式(22),就可以根据屈服强度来获得抗拉强度,为后续延伸率的预测奠定基础。
图6 不同热处理条件下及在180 ℃不同二次枝晶臂间距(d)条件下Al-7Si-0.36Mg合金(σUTS-σY)随σY的变化规律
Fig.6 Curves of (σUTS-σY) vs σY for Al-7Si-0.36Mg cylindrical samples at different heat treatments (a) and with different secondary dendrite arm spacings (d) aged at 180 ℃ (b)
3 模拟结果及验证
在本模型中,一些关键参数需要进一步说明:(1) 从TEM像可知,β"相是Al-7Si-Mg合金中的主要析出相,特别是在欠时效和峰时效阶段。此外,研究表明[35,36],针状β"相的成分为Mg5Si6;(2) 本工作的一些参数通过Pandat数据库获得,如相图平衡成分、扩散系数等;(3) 在不同文献中,对析出相形貌的假设不同,通常析出相的 在1.8~5.0 nm之间,本工作 取值2.4 nm,与Wang等[37]的理论数值2.5 nm接近;(4) 由于参数k1、 难以确定,本工作主要通过调整k1、 ,以模拟和实验结果相吻合为标准,来确定合理的k1、 值,进而确定其它热处理条件下的数值。计算中所用到的参数的取值参见表3。
3.1 析出相尺寸及屈服强度计算
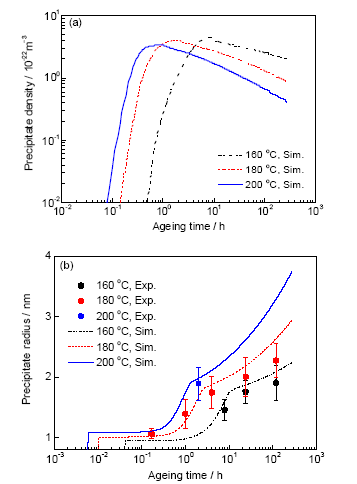
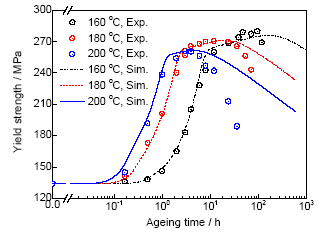
首先采用时效析出动力学模型,模拟该合金在160、180和200 ℃ 3组时效温度下的析出相密度和平均半径随时效时间的变化,如图7所示,并与表2中的析出相半径实测结果进行对比,以确定析出相的密度和半径。以180 ℃下的模拟结果为例,在时效初期(t<0.5 h),析出相密度快速增加,而析出相半径几乎不变。当时效时间达到1.8 h时,析出相密度达到了最大值,析出相半径快速增大。随着时效时间进一步延长,析出相密度开始降低,而析出相半径继续增大。比较3组时效温度下的时效析出动力学可知,时效温度的提高会极大地促进时效析出过程。从图7b中的析出相平均半径模拟结果和实验值的比较可看出,本模型可以较好地预测析出相半径的变化规律。图8为3组时效温度下的屈服强度模拟结果和实验结果比较。可以看出,在欠时效和峰时效阶段,模拟结果与实验结果吻合很好,但是在过时效阶段,两者之间误差较大,并且随着时效时间的延长和时效温度的提高,两者之间误差逐渐增大。这主要是因为本模型没有考虑在过时效阶段形成的、与基体半共格的棒状β'相和非共格的β平衡相。由于β"相与基体之间的点阵参数常数差值要比β'或β相的大[40],所以,β"析出相强度相对于相同尺寸的β'或β析出相要大一些,而析出相强度越大,合金的强度就越高(见式(6))。综合图7中析出相特征参数和图8中的屈服强度模拟结果可知,该合金屈服强度在0~4 h内快速增大主要源于析出相的快速形核与生长;在时效时间4~24 h区间,析出相的密度减小和尺寸的增大,导致该合金在该时间段内屈服强度缓慢增大;在过时效阶段(>24 h),析出相密度减小对屈服强度的影响大于析出相尺寸增大的影响,从而导致合金屈服强度开始降低。
图7 3组时效温度下Al-7Si-0.4Mg合金析出相密度和半径随时效时间的变化
Fig.7 Densities (a) and mean radii (b) of β" precipitates as a function of ageing time for Al-7Si-0.4Mg alloy aged at 160, 180 and 200 ℃
图8 Al-7Si-0.4Mg合金在3组时效温度下的屈服强度模拟结果与实验结果对比
Fig.8 Comparisons of predicted and measured yield strengths for Al-7Si-0.4Mg alloy aged at 160, 180 and 200 ℃
3.2 应变硬化行为模拟研究
3.2.1 时效处理对Al-7Si-Mg合金应变硬化行为的影响 为了考虑晶界和共晶硅对随动硬化的影响,式(16)和(17)中的3个参数N*、λ和D分别取值为6.5、160 nm和5.0 μm。图9给出了最薄阶梯中二次枝晶臂间距为24.9 μm的片状拉伸试样在屈服以后应力增量随应变增量的变化曲线(σ-σY,ε-εY)。表4给出了每一时效时间内由时效析出动力学模型计算得到的基体中的Mg含量、计算中所采用的参数k1和 取值以及根据应力-应变曲线获得的特征参数θ0和K(式(1))。从图9和表4可以看到,淬火态试样的位错存储速率k1和动态回复速率 取值较小,合金的硬化速率较小,塑性变形能力强。经过0.5 h时效处理以后,k1从1.65增大至2.10,而 变化较小(基体中元素含量变化较小),从而使得合金的硬化速率明显增大。对于经过时效1 h后的试样,k1增加至2.65, 增加至20,其中 的变化主要源于析出相的形成消耗了基体中大量的合金元素。k1和 增大,使该合金在低应变下的硬化速率dσ/dε增大,在高应变下的硬化速率减小(图9a)。当时效时间超过1 h,k1不再发生变化,而对于 ,在1~4 h区间,由于析出相的形核与生长消耗了基体中的Mg和Si元素,使 从20增加至28,在4~12 h区间,虽然基体中的Mg元素已经基本完全消耗,但是 却发生明显增大,这可能是因为Si颗粒的析出消耗了基体中剩余的Si。因此,可以推断 的变化与基体中的合金元素含量密切相关,这与文献[13,31] 中报道的结论是一致的,而k1似乎并不受基体中元素含量变化的影响。k1的变化主要发生在时效初期,可能是由于在该阶段的一些微观结构变化,如空位、原子偏聚等所引起的。当时效时间超过12 h后,k1和 恒定不变,应力-应变曲线的变化主要由基体中的析出相决定,因为析出相周围形成的位错环密度会随着析出相尺寸的增大逐渐增加,这一方面会使动态恢复系数k2增大(式(21)),另一方面会导致随动硬化效果Δσkin_p。根据表4中的结果可以发现,初始硬化速率θ0在时效1 h后变化很小,与k1的变化规律类似,而参数K的变化规律则与 的类似。
图9 Al-7Si-0.36Mg合金(d=24.9 μm)在180 ℃时效不同时间后的应力-应变曲线实验和模拟结果对比
Fig.9 Experimental and simulated stress-strain curves of Al-7Si-0.36Mg alloy (d=24.9 μm) after aged at 180 ℃ for different times
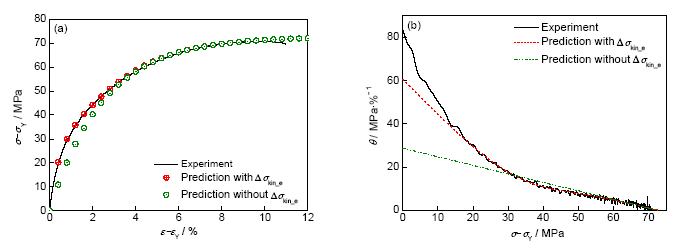
3.2.2 铸态组织细化程度对Al-7Si-Mg合金应变硬化行为的影响 除了基体中的合金元素及析出相组织之外,凝固过程形成的枝晶、共晶、金属间化合物等组织也会影响合金在拉伸过程的应力-应变曲线及硬化行为。对于Al-7Si-Mg合金,一般采用二次枝晶臂间距d来表征该合金组织的细化程度,d越小,晶界面积越大,共晶硅颗粒尺寸越小。图10给出了本模型在考虑和不考虑Δσkin_e时,应力-应变曲线和硬化速率θ的模拟结果与实验结果的比较,其中试样d为24.9 μm,并在180 ℃下时效2 h。可以看出,在考虑Δσkin_e时的模拟结果与实验结果的吻合程度要明显优于不考虑Δσkin_e的情况,这说明晶界和共晶硅颗粒对随动硬化效果的确具有重要的影响,要准确模拟应力-应变曲线,必须要合理地考虑这些因素。
图10 Al-7Si-0.36Mg合金中晶界和共晶硅颗粒所引起的随动硬化效果Δσkin_e对合金应力-应变曲线(σ-σY~ε-εY)以及硬化速率的影响
Fig.10 Influences of kinematic strain hardening (Δσkin_e) caused by grain boundary and eutectic silicon particles on the stress-strain curves (a) and strain hardening rate (b) in Al-7Si-0.36Mg alloy
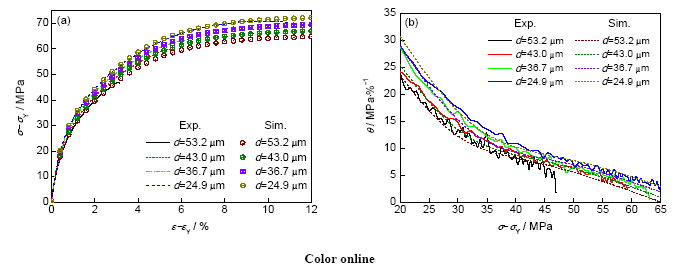
图11给出了4种二次枝晶臂间距(53.2、43.0、36.7和24.9 μm)的Al-7Si-0.36Mg合金试样,在180 ℃时效2 h后的应力-应变曲线及硬化速率曲线。表5中所示为4种二次枝晶臂间距试样的k1、 和D参数。可以看到,随着d的减小,位错存储速率k1增大(表5),应力值(σ-σY)增大(图11a)。d越小,晶界面积和共晶硅颗粒密度越大,从而使位错更容易塞积,位错密度越高,导致k1越大。此外,d的变化并不影响位错动态回复速率 (表5)。组织细化除了影响k1之外,还会影响参数D (表5),这主要是因为D是与枝晶细化程度和共晶硅颗粒尺寸或密度相关的参数。一般枝晶组织越细,晶界面积和共晶硅颗粒密度(尺寸越小)越大,D越小,在小应变量阶段造成的随动硬化效果Δσkin_e越大,从而导致合金的θ0越大,如图11b中所示。
图11 二次枝晶臂间距对Al-7Si-0.36Mg合金拉伸过程的应力-应变曲线和硬化速率的影响
Fig.11 Influences of d on the stress-strain curves (a) and strain hardening rate (b) in Al-7Si-0.36Mg alloy
3.3 抗拉强度和延伸率的预测及实验验证
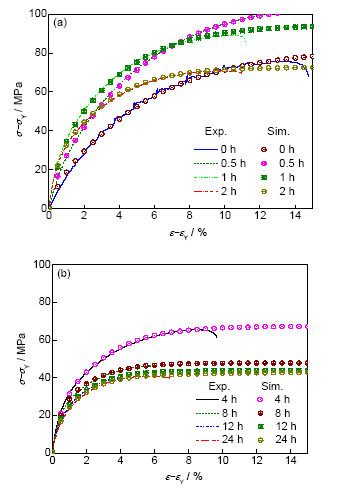
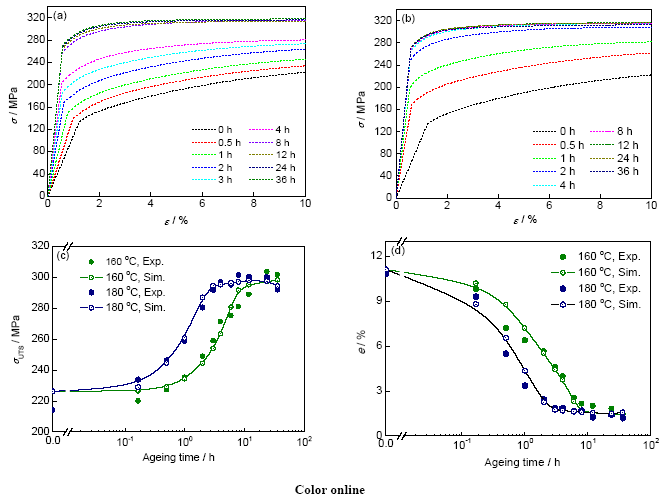
本工作预测抗拉强度和延伸率的思路是:首先根据时效析出动力学模型和强化模型计算该合金在时效过程的屈服强度σY (图8),然后根据屈服强度和抗拉强度之间的关系式(式(22))计算对应的抗拉强度,最后采用应变硬化模型计算拉伸过程的应力-应变曲线,并结合抗拉强度来计算延伸率。Al-7Si-0.4Mg合金拉伸试棒的d为45.2 μm,因此根据文中m和n的表达式,计算得到m=-0.472,n=155.6。图12所示为Al-7Si-0.4Mg合金拉伸试样,在160和180 ℃时效0~36 h后的工程应力-工程应变曲线模拟结果及对应的抗拉强度和延伸率的模拟与实验结果比较。从图12a和b可以看出,在160 ℃时效12 h或180 ℃时效4 h后,随着时效时间的延长,由于屈服强度和应变硬化行为的变化较小,合金的应力-应变曲线变化也较小。此外,随着时效时间的延长,材料的Young's模量增大(式(9)),使得屈服强度对应处的应变εY减小。需要指出的是,本模型并不关注材料在屈服之前的应力-应变曲线的变化,因此用直线来近似表示之。从图12c和d可以看出,该模型预测结果可以较好地反映Al-7Si-Mg合金在时效过程抗拉强度和延伸率的变化规律,并且两者之间的偏差不大,满足工程上应用的误差需求。需要进一步说明的是,对于时效时间较长的试样,由于材料的动态回复速率参数k2较大,导致该合金在较大应变量处(>2%)的应变速率较小,所以当计算的抗拉强度存在较大误差时,预测的延伸率也会产生较大误差,而抗拉强度的预测精度,取决于屈服强度计算精度,以及屈服强度和抗拉强度之间关系式(式(22))的拟合程度。因此本模型中的屈服强度、抗拉强度和延伸率的计算精度是相互影响的。
图12 Al-7Si-0.4Mg合金拉伸试样在160和180 ℃下时效0~36 h的工程应力-工程应变曲线模拟结果以及抗拉强度和延伸率的模拟结果和实验值的比较
Fig.12 Predicted engineering stress-engineering strain curves (a, b) of tensile samples of Al-7Si-0.4Mg alloy aged at 160 ℃ (a) and 180 ℃ (b) for 0~36 h, and the comparisons of predicted and experimental ultimate tensile strengths (c) and elongations (d)
本模型中组织的细化程度对于屈服强度的影响主要体现在式(5)中的参数?σ0,通过实验数据拟合出?σ0的经验性表达式:
(23)
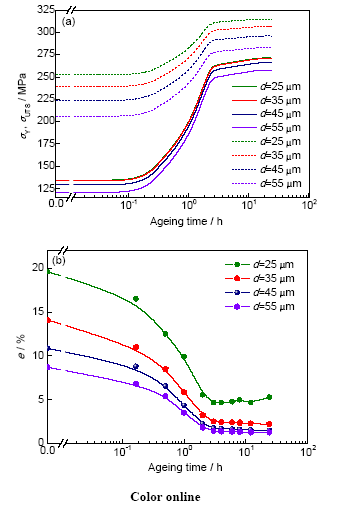
式中, 和 分别为基体中Mg和Si的含量, 和 分别为Mg和Si原子的固溶强化系数, 为固溶时间。该方程考虑了二次枝晶臂间距(等式右边第一项)、固溶时间和温度(等式右边第三项)以及合金成分(等式右边第二项)对Al-7Si-Mg合金屈服强度的影响。模型还考虑了组织的细化程度对于抗拉强度和延伸率的影响,主要体现在屈服强度和抗拉强度之间的关系式(式(22))以及位错存储速率参数k1 (表5)。因此,采用本模型模拟了180 ℃时效条件下,4种二次枝晶臂间距(55、45、35和25 μm)的Al-7Si-0.4Mg合金拉伸试样的屈服强度、抗拉强度和延伸率,结果如图13所示。可以看出,随着d的减小,合金的力学性能提高,特别是当d从35 μm减小到25 μm时,合金的延伸率有较大的改善。此外,合金的强度越高,延伸率越小,若要改善合金的延伸率,可考虑适当降低其强度。
图13 不同二次枝晶臂间距的Al-7Si-0.4Mg合金拉伸试样在180 ℃时效0~24 h的屈服强度、抗拉强度和延伸率模拟结果
Fig.13 Predicted yield strength, ultimate tensile strength (a) and elongation (b) of the tensile samples in Al-7Si-0.4Mg alloy with different secondary dendrite arm spacings after aged at 180 ℃ for 0~24 h (Solid lines and dash lines in Fig.13a represent the yield strength and ultimate tensile strength, respectively)
4 模型的局限性及影响力学性能预测精度的因素分析
影响Al-7Si-Mg合金最终力学性能的影响因素很多,如枝晶组织、共晶组织、缺陷组织、析出相组织以及基体中的溶质成分等,而这些组织受凝固条件、热处理条件以及合金成分等因素的影响。Al-7Si-Mg合金的屈服强度主要由析出相的密度、尺寸等相关参数决定,同时也受枝晶和共晶硅组织的影响[41,42]。枝晶组织主要由凝固条件决定,而共晶硅颗粒除了受凝固条件影响外,还与固溶处理条件密切相关,因此凝固条件和固溶处理条件也会影响该合金最终的屈服强度。为了考虑这种影响,本工作在强化模型中用?σ (淬火态的屈服强度减去此时的固溶强化效果)综合表征凝固和固溶处理条件对合金屈服强度的影响。不过所采用的?σ0值是通过实验数据获得的,这表明该模型计算时需要一些实验数据。此外,Al-7Si-Mg合金的时效过程经历[43]:过饱和固溶体(SSS)→原子偏聚区(GP区)→β"(Mg5Si6)→β'(Mg9Si5)→β (Mg2Si)。在欠时效和峰时效阶段,基体中主要以与基体共格的针状β"相为主,它是主要的强化相,而在过时效阶段,由于与基体半共格的棒状β'相或非共格的盘片状β相的形成,一方面会改变析出相长径比及其成分,同时也会改变析出相的强化效果。不过本工作建立的时效析出动力学模型中,只考虑了针状的β"相,并且假定析出相的长径比和界面能在时效过程中恒定。显然,这些假设条件会影响屈服强度的计算精度,如图8中所示。
抗拉强度的计算依赖于屈服强度的计算结果(式(22)),所以屈服强度的计算误差会影响抗拉强度的计算精度。对于Al-7Si-Mg铸造铝合金,组织中一般都会存在一定数量的缩孔,同时还存在脆性共晶硅相,一般枝晶组织越粗大,缩孔尺寸和共晶硅颗粒尺寸越大,合金的抗拉强度和延伸率越低。本工作为了考虑枝晶组织差异对合金抗拉强度的影响,通过实验数据拟合出了式(22)中参数m、n随二次枝晶臂间距变化的表达式,再通过在式(22)中引入f(Tss)以考虑固溶温度对抗拉强度的影响。由于公式(22)是采用欠时效和峰时效的试样数据拟合得到的,所以该公式不适用于该合金在过时效阶段的抗拉强度预测。
延伸率的计算主要依赖于抗拉强度以及应力-应变曲线。由于式(22)不能计算过时效阶段的抗拉强度,所以本模型也无法计算过时效阶段的延伸率。由于在大应变量处应力随应变的增加速率比较小(图9和12),所以当抗拉强度预测偏差较大时,会对延伸率的预测精度产生较大影响。此外,应力-应变曲线的计算结果也是影响延伸率计算精度的重要因素,其中参数k1和 的选择对于应力-应变曲线的计算至关重要,而决定这2个参数大小的因素很多,因此如何更加合理地选择参数k1和 ,仍需进一步研究。
5 结论
(1) 建立了Al-7Si-Mg合金时效析出动力学模型、强化模型和应变硬化模型,预测出合金的拉伸性能。结合时效析出动力学模型和强化模型可以计算β"析出相微观组织参数和合金屈服强度。应变硬化模型中考虑了各向同性硬化和随动硬化,以及析出相的形成和基体中成分变化对位错存储速率和动态回复速率的影响,这些模型可以模拟合金拉伸过程的应力-应变曲线,结合(σUTS-σY)~σY关系式,可以计算合金抗拉强度和延伸率。
(2) 本模型在预测过时效试样的屈服强度时存在较大误差,可能原因是本模型仅考虑了β"析出相以及采用恒定的析出相长径比和界面能。时效处理会影响参数k1和 ,其中k1的变化主要发生在时效初期, 的变化取决于基体中的元素含量。组织细化程度会影响参数k1,二次枝晶臂间距越小,k1越大。
(3) 预测了Al-7Si-0.4Mg合金在不同时效温度下的抗拉强度和延伸率,实验结果和模拟结果较为吻合,同时研究了二次枝晶臂间距对拉伸性能的影响规律。并分析了本模型存在的局限性以及影响拉伸性能预测精度的因素。
 , 郭会廷
, 郭会廷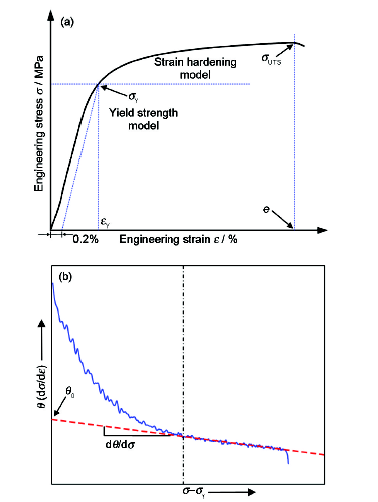







 沪公网安备31011202020290号
沪公网安备31011202020290号
