分享：基于GA-ELM的铝合金压铸件晶粒尺寸预测

梅益1, , 孙全龙1, 喻丽华1, 王传荣2, 肖华强1

1 贵州大学机械工程学院 贵阳 550025
2 中国石油新疆独山子石化分公司 克拉玛依 833699

摘要

关键词： 铝合金 ; 微观组织 ; 晶粒尺寸 ; 极限学习机 ; GA-ELM模型

晶粒尺寸是决定材料机械性能最本质的因素之一,对铝合金压铸件晶粒尺寸的控制是获得高质量压铸件的关键。在考虑到压铸件缺陷最小的同时,在实际的压铸工艺制定过程中应选取获得最小平均晶粒尺寸的压铸工艺参数。因此,铝合金压铸件晶粒尺寸的有效预测对合理制定压铸工艺参数、提升产品质量具有重要意义。

传统的晶粒尺寸预测方法包括利用模拟软件进行模拟、经验法等[1,2]。模拟软件进行模拟的预测方法是应用Anycasting或Procast等铸造过程仿真软件对铸件晶粒尺寸进行预测,Anycasting或Procast等铸造过程仿真软件是采用基于有限元(FEM)的数值计算和综合求解的方法,对铸件充型、凝固和冷却过程提供模拟,基于强大的有限元分析及微观组织模块,它能够较为准确地预测铝合金压铸件成型的晶粒尺寸,但是它的问题是,面对复杂铸件时,计算的耗时非常长,晶粒尺寸预测效率低[3,4];经验法是指压铸工艺人员通过自身的生产经验对某组压铸工艺参数条件下将得到的铸件的晶粒尺寸提前预测,根据经验匹配最优工艺参数组合以获取晶粒尺寸最小的铸件。经验法耗时短、效率高,但是它的问题是非常依赖于工艺人员自身经验及技术水平,对压铸件晶粒尺寸的预测精度很低[5]。针对传统的晶粒尺寸预测方法存在的问题,訾炳涛等[6]和刘彬等[7]提出了应用BP神经网络算法模型预测铸件晶粒尺寸的方法,虽然该方法在一定程度上解决了传统的晶粒尺寸预测方法效率与精度不能兼得的问题,但是该模型自身存在易陷入局部最优解、网络结构不易确定的问题,进而影响了预测精度;唐江凌等[8]提出了应用支持向量机算法模型预测合金晶粒尺寸的方法,该模型具有拟合精度高、泛化能力强的优点,但是也存在参数确定困难的问题,进而影响了预测效率;传统的学习算法(如BP算法、支持向量机等)固有的一些缺点,成为制约其发展的主要瓶颈,也阻碍了其在晶粒尺寸预测方面的应用。Huang等[9]针对传统算法的固有缺点提出了一种特殊的单隐含层前馈神经网络模型-极限学习机,与传统算法相比,该算法具有参数设置少、学习速度快和泛化性能好的优点,但是该算法随机产生输入层到隐含层的权值矩阵及隐含层阈值矩阵,对结果影响较大,不易获得最优极限学习机(ELM)模型进行预测[10]。因此,需要找到一种适用于这类复杂问题的方法,准确、高效地预测铝合金压铸件晶粒尺寸。

本工作研究了一种结合遗传算法(GA)和极限学习机(ELM)的GA-ELM模型,分别利用GA-ELM模型、原始ELM模型和BP神经网络模型,对相关实验数据进行拟合及预测,并对比三者的拟合精度和效率,以证明GA-ELM模型的有效性和实用性。

1 GA-ELM流程

1.1 ELM基本原理

ELM是一种特殊的单隐含层前馈神经网络模型,它的输入层权值矩阵和隐含层阈值矩阵是随机产生的,并且在之后的运算中无需调整。研究[11,12]表明,只需要设置隐含层节点的数量,便可以获得唯一的最优解。

对于给定的输入样本X,隐含层神经元的输出矩阵H的计算公式为[11]：

$\begin{array}{c}?=?(?{?}^{?}+?)\end{array}$(1)

式中,W为输入层权值矩阵,b为隐含层阈值矩阵,W和b随机产生;g为隐含层神经元激活函数。

ELM神经网络的输出值P为[11]：

$\begin{array}{c}?=\left({?}^{?}?\right)\end{array}$(2)

式中,β为隐含层到输出层的权值矩阵,只要确定β即可唯一确定ELM神经网络。

对于给定的训练输出样本Y,用输出样本替代网络输出值,则β可以通过求解以下方程组的最小二乘解获得[11]：

$\begin{array}{c}\underset{?}{\mathit{min}}‖{?}^{?}?-?‖\end{array}$(3)

方程组(3)的最小二乘解 $\begin{array}{c}\stackrel{\wedge }{?}\end{array}$为[11]：

$\begin{array}{c}\stackrel{\wedge }{?}=({?}^{?}{)}^{+}?\end{array}$(4)

式中,(HT)+为转置矩阵HT的Moore-Penrose广义逆。

1.2 GA优化ELM模型

由以上ELM基本原理可知,W和b可随机产生。因此在隐含层节点相同的条件下,使用同一个训练样本集训练ELM模型,由于W和b随机产生,会造成网络拟合出的晶粒尺寸变化很大。GA具有很强的全局寻优能力,利用GA为ELM模型寻找最优的初始W和b,可以提高ELM模型的拟合精度,获取最优ELM模型。

GA-ELM训练步骤如下：

(1) 首先读入实验数据。将实验数据分成训练集和测试集,并将数据进行归一化处理,避免因实验数据数量级相差较大而造成预测误差较大。

(2) 调用GA寻找ELM算法最优的初始W和b。种群中的每个个体都包含了一个ELM网络的所有权值和阈值,个体通过适应度函数计算个体适应度值,遗传算法通过选择、交叉和变异操作找到最小适应度值的对应个体。个体适应度函数取为ELM网络对训练集中部分样本预测的平均误差[11]：

$\begin{array}{c}\mathit{error}=\frac{\sum ^{}\left|{?}_{\mathit{ij}}-{?}_{\mathit{ij}}\right|}{?}\end{array}$(5)

式中,yij为训练集中部分样本的输出预测值,xij为训练集部分样本真值,N为训练集部分样本个数。

(3) 用遗传算法得到最优个体对ELM的初始权值和阈值赋值,并设置隐含层节点个数,完成GA-ELM模型的建立。

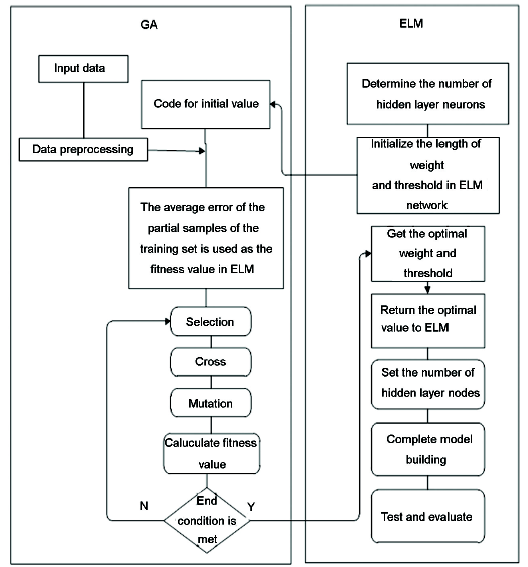
(4) 利用测试集样本对GA-ELM模型进行测试及效果评价。其算法流程如图1所示。

图1   遗传算法-极限学习机(GA-ELM)算法流程

Fig.1   An algorithm flow of genetic algorithms-extreme learning machine (GA-ELM)

2 基于GA-ELM的铝合金压铸件晶粒尺寸预测模型

2.1 训练集样本数据的获取

首先,选取与凝固过程密切相关的压铸工艺参数作为输入参数,输入参数选定为模具预热温度TP、压射温度TI、低速充型速度VS和高速充型速度VF 4个参数;然后,由于压铸件不同位置晶粒尺寸不相同,所以选取铸件上对机械性能要求较高的部位截面的平均晶粒尺寸作为输出参数;最后,通过实际压铸生产,对不同的输入参数进行实验,获得相应压铸件,对其进行金相分析后获得不同条件下的平均晶粒尺寸。

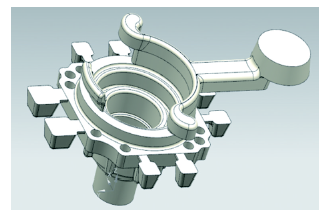
图2   汽车空压机端盖压铸件几何模型

Fig.2   Geometric model of die casting of automobile air compressor end cover

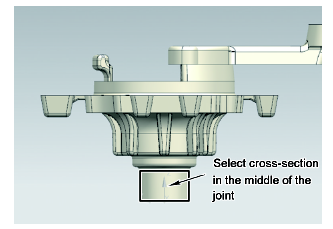
以汽车空压机端盖的压铸成型为例,其几何模型如图2所示。轮廓尺寸112 mm×112 mm×84 mm,平均壁厚5 mm,材料为铝合金ADC12。汽车空压机端盖接口部位几何模型如图3所示。此部位要求常温下力学性能优良,晶粒尺寸细小,因此选取该部位中间截面的平均晶粒尺寸(以下简称晶粒尺寸)作为实验的输出参数,同时根据压铸生产经验确定模拟实验的输入参数及水平设置,如表1所示。

图3   汽车空压机端盖接口部位几何模型

Fig.3   Geometric model of the joint of automobile air compressor end cover

采用四因素四水平正交实验法对该铸件的压铸工艺方案进行优化设计,即L32(45)正交表,共32组实验。利用这32组压铸工艺方案进行实际压铸生产,对生产得到的压铸件进行金相实验并测量其晶粒尺寸,获得不同工艺参数条件下的晶粒尺寸,这32组样本作为训练集,工艺参数的正交实验表及晶粒测量结果如表2所示。遗传算法优化中的个体适应度值取为训练集中No.27~No.32共6个样本的预测平均误差值。

2.2 GA-ELM参数设置

利用表2中的训练集样本数据对GA-ELM算法模型进行训练。GA-ELM模型完整地保留了GA和ELM算法中的可调参数,这些参数的选取可以参考ELM和GA算法的相关文献[13~26]。本工作通过多次调整相关参数,将得到的最终的实验结果进行对比,给出效果最好的一组推荐值,如表3所示。

2.3 测试集样本数据的获取

测试集样本数据工艺参数的选取如表4所示,同样通过压铸生产实验获得相应晶粒尺寸。

2.4 预测效果及分析

遗传算法优化的进化结果如图4所示,即为个体适应度值变化曲线。可以看出,遗传算法部分收敛得很好,在30代时已基本收敛至最优权值和阈值。由于其权值矩阵和阈值矩阵规模较大,其具体取值不再赘述。

图4   遗传算法进化结果

Fig.4   Evolution consequences of the GA optimization

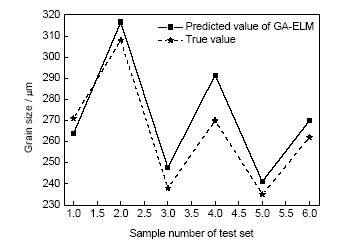
利用建立完成的GA-ELM模型对测试集数据进行预测,并与测试集输出真值进行对比,如图5所示。可以看出,除第4组样本外,其它测试集样本误差均控制在10 μm以内,第4组样本误差也不超过22 μm。考虑到本工作研究微观尺寸下的晶粒,微观尺寸内存在一定的扰动因素,并且训练使用的样本数量较少,拟合度有限,因此不超过22 μm的最大误差属于可以接受的最大误差值。同时,通过计算,测试集样本数据预测平均绝对误差为10.2 μm,平均相对误差为3.8%。可见,GA-ELM模型可以准确、有效地对晶粒尺寸进行预测。

图5   GA-ELM模型对测试集样本的预测结果与测试集输出真值对比

Fig.5   Comparisons between predicted results of GA-ELM model and output true values of test set

2.5 与其它模型预测结果对比

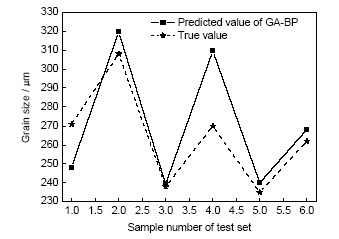
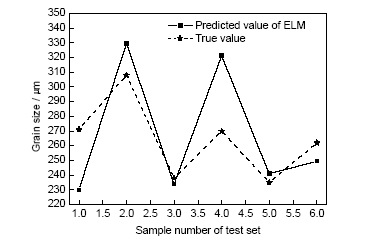
为了体现该模型的优越性,采用GA-BP神经网络及原始ELM模型对该样本进行预测,其中原始ELM模型隐含层节点数为60 (多次实验确定),隐含层激励函数选择“sigmoid”函数;GA-BP神经网络模型隐含层节点数设为25 (多次实验确定),隐含层激励函数选择“logsig”函数。GA-BP神经网络模型及原始ELM模型的测试集样本预测结果及输出真值分别如图6和7所示。

图6   GA-BP模型对测试集样本的预测结果与测试集输出真值对比

Fig.6   Comparisons between predicted results of GA-BP model and output true values of test set

图7   ELM模型对测试集样本的预测结果与测试集输出真值对比

Fig.7   Comparisons between predicted results of ELM model and output true values of test set

以上3种模型的预测结果对比情况见表5。可以看出,GA-ELM模型在预测精度上要明显优于其它2个模型。但由于采用了遗传算法,GA-ELM模型的训练效率要远低于原始ELM模型。但是,即使如此,GA-ELM模型的训练效率也要远高于GA-BP模型,其效率是可以接受的。综上所述：GA-ELM模型具有较高的预测精度,可以相对准确地预测铝合金压铸件的晶粒尺寸。但该模型的预测效率相对较低,虽然可以接受,但还有提高空间。

3 实验验证

为验证GA-ELM算法可靠性,制定一组压铸工艺参数进行实验验证。TP设为660 ℃,TI设为210 ℃,VS设为0.3 m/s,VF设为5 m/s,通过GA-ELM模型预测该组压铸工艺参数对应的晶粒尺寸D,预测值为267 μm。同时,对该压铸工艺参数条件下生产的汽车空压机端盖的接口部位的金相组织进行观察及几何测量,选取同一截面的3个不同部位,其金相组织如图8所示。通过截线法分别获得3个位置的平均晶粒尺寸后,将这3个值再次平均代表整个截面的平均晶粒尺寸,为258.5 μm,与GA-ELM模型预测值相差8.5 μm,相对误差为3.18%。可见,GA-ELM模型预测效果极好。

图8   汽车空压机端盖接口部位同一截面不同位置的金相组织

Fig.8   Metallographic microstructures of different positions (a~c) on the same cross-section of the joint of automobile air compressor end cover

4 结论

(1) 提出了应用遗传算法-极限学习机(GA-ELM)模型预测铝合金压铸件晶粒尺寸的方法。采用GA对ELM的输入层权值矩阵和隐含层阈值矩阵进行优化,避免了输入层权值矩阵和隐含层阈值矩阵随机性对ELM预测精度的影响,提高了预测准确率。丰富了铝合金压铸件晶粒尺寸预测方法。

(2) GA-ELM模型是一种高精度、较高效、满足工程要求的模型。其预测精度高于GA-BP模型和原始ELM模型,训练效率高于GA-BP模型,但低于原始ELM模型。

(3) 通过实际压铸生产及金相组织测量实验,验证了GA-ELM模型预测铝合金压铸件晶粒尺寸的可靠性。

来源--金属学报