分享:W1 - x Ir x 固溶合金几何结构、电子结构、力学和热力学性能的第一性原理计算
1.
2.
3.
利用基于密度泛函理论的第一性原理方法结合声子谱计算和价键作用分析,研究了Ir含量对W1 - x Ir x (x = 0~12.96,原子分数,%)合金几何结构、相稳定性、力学性能以及热力学稳定性的影响,构建了Ir的添加量与W-Ir合金的相稳定性、力学以及热力学性能的变化关系。发现W-Ir合金的相稳定性随着Ir含量的增加而逐渐降低,这与W—Ir价键中部分反键态占据Fermi能级以下区域有关;Ir在W中的添加量小于7.4%时,W-Ir合金满足基态相稳定性要求;随着温度的升高以及Ir含量的增加,W-Ir合金的热力学稳定性得到提升,表明Ir适合添加到高温条件下应用的W中;Ir的加入能降低剪切模量,改善钨合金韧性,与实验观察一致,但Ir也能提升平面抗剪切变形能力。本征脆性的Ir对W的强韧化作用与W—Ir原子键合时轨道电子的转移和重叠方式有关。
关键词:
难熔金属W因为具有高熔点(3410℃)、高硬度、高强度、高密度(19.32 g/cm3)、良好的耐化学腐蚀性和抗烧蚀性等特点,可用作能源、冶金、化工、电子等民用领域,以及国防军工、航空航天、新能源、核工业等尖端科技领域的关键支撑材料[1]。其中,在航空航天领域应用的固体火箭燃料发动机非冷却式喷管中所用的W,需具有耐高温、抗热震和耐侵蚀等特性,使其在高温条件下服役较长时间而不失效[2~4]。但纯W具有低温脆性易裂、不易加工以及高温强度不足的问题,抗蚀性也有待加强。固溶合金化方法可以有效改善这些问题[5,6]。如Re元素自从1956年被Geach和Hughes[7]发现能改善W的塑性以来,在各种成分范围(0~50%,原子分数)内的合金化作用均已被广泛研究。与Re具有相似电子结构的Ir也引起研究者们的关注。贵金属Ir密度略低于Os,熔点高(2447℃)、硬度高、弹性模量高,具有极强的耐腐蚀性、热稳定性及高温强度等性能。就化学稳定性而言,它是金属中最耐腐蚀的元素,不溶于所有的无机酸,包括王水,能经受许多熔融试剂和高温硅酸盐的侵蚀。Ir的这些物化性能使它能在非常苛刻的条件下工作,在传统高温材料领域获得应用,适合添加到钨基合金中使其能更好地在高温特殊环境下服役。Luo等[8,9]分别研究了W-0.4%Ir和W-0.8%Ir (质量分数)中Ir含量对W的室温以及高温力学性能的影响,并与Re做对比。研究表明,Ir对W的室温韧化性能可以与Re相媲美,而且可以较好地维持W的高温强度。McKamey等[10]发现,0.3%Ir (质量分数)可以提升钨合金韧性的程度为9%~15%。但让研究者费解的是,Ir具有fcc结构,然而却具有不同于常规fcc结构的力学性能,比较脆,一般认为只有在1600℃以上才具有良好的塑性[11,12]。研究表明,Ir具有更多的价电子因此导致其价键具有明显的方向性[13],其金属键具有伪共价(pseudo-covalent)特征[14]。具有脆性特征的Ir元素能较好地起到韧化钨合金的作用,这种奇妙特性转变的内在影响因素和作用机制尚未揭示。除此之外,目前关于Ir的添加量和其固溶合金化所带来的力学以及热力学性能方面的变化关系尚未建立。因此从微观尺度上研究Ir的加入对钨基合金性能的影响非常必要,也具有重要意义,有助于研究者们更好地基于Ir对W的影响特性设计W-Ir合金的成分,拓展钨基合金在高温领域的应用。
考虑到基于密度泛函理论的第一性原理计算可以很好地揭示合金元素和基体元素间的电子相互作用和价键本质,比较准确地预测材料的力学及性质,本工作采用第一性原理方法研究了0~12.96%Ir (原子分数,下同)添加到钨基合金后的相稳定性、晶体结构、弹性力学性能以及热力学性能的变化,揭示了偏脆的Ir对W的强韧化作用的本质。
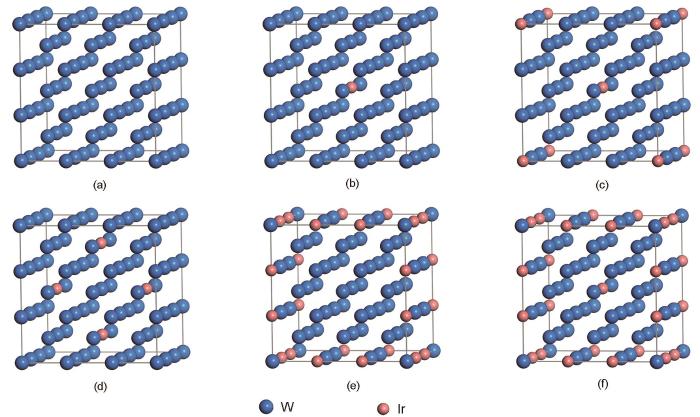
基于实验背景考虑,针对bcc结构的W构建了W-Ir合金的超单胞模型W1 - x Ir x ,x的变化范围为0~12.96%,模型示于图1。
图1 W-Ir固溶合金模型示意图
(a) W (b) W98.15Ir1.85 (c) W96.30Ir3.70 (d) W92.59Ir7.41 (e) W88.89Ir11.11 (f) W87.04Ir12.96
Fig.1 The illustrations of W-Ir solid solution models
形成能(ΔE)主要用于表征固溶合金的相对稳定性,是衡量合金元素对基体材料影响的重要参数。计算公式如下[15]:
式中,E(W1 - x Ir x )、E(W)、E(Ir)分别表示充分弛豫后的W1 - x Ir x 合金、W单质、Ir单质中单个原子的能量。计算所得形成能是平均后的单个原子形成能。
式中,BV、GV和BR、GR分别为按照Voigt和Reuss方法所得体积模量和剪切模量;Cij 、Sij 分别是弹性系数和应变系数。由Voigt-Reuss-Hill[20]近似得到:
另外,采用Pugh值(G / B)和Cauchy应力Cp= (C12 - C44)来衡量W-Ir合金的韧脆性变化[21]。G / B <0.5预示材料呈现韧性,而相反地,G / B > 0.5预示材料呈现脆性。Cp > 0预示材料呈现韧性,Cp < 0预示材料呈现脆性。
式中,E0(V)表示0 K时的基态能量,Fel(V, T)为电子自由能,Fvib(V, T)为晶格振动自由能,U为内能,V为体积,T为温度。
为了进一步探究相稳定、力学及热力学性质产生的物理根源,有必要研究基体元素和添加元素之间的价键作用。但是基于投影缀加波(PAW)交换关联势的密度泛函理论方法得到的电子结构无法直接给出原子之间的价键作用信息,因此本工作进一步计算了投影晶体轨道Hamilton布局(projected crystal orbital Hamiltonian population,pCOHP)[24],对原子轨道电子重叠情况进行分析。pCOHP是一种将密度泛函理论所得到的能带波函数原子轨道化处理的方法,是Deringer等[24]在1983年Hughbanks和Hoffmann[25]提出的晶体轨道重合布局(crystal orbital overlap population,COOP)和1993年Dronskowski和Bl?ch[26]发展的晶体轨道Hamilton布局(crystal orbital Hamilton population,COHP)分析的基础上进一步发展起来的。在pCOHP方法中,依次对能带波函数进行转移矩阵(包含单电子轨道函数)处理、投影密度矩阵(包含基于原子轨道线性组合获得的相关原子轨道化学信息)处理、Hamilton矩阵化处理,最后将该Hamilton布局权重作用到态密度曲线上,所得即pCOHP曲线[24]。曲线包含成键和反键轨道电子信息,成键轨道电子引起能量下降,而反键轨道电子引起能量增加,可以定量表征键强,适用于共价键、离子键、金属键以及分子键体系[24]。本工作中,pCOHP曲线基于面向电子结构重建的局域轨道基组(local orbital suite towards electronic-structure reconstruction,LOBSTER)程序[27]计算获得。除此之外,本工作利用二次差分电荷密度来分析掺杂前后电子的转移以及空间分布情况。
Table 1 Comparisons between the calculated lattice constant (a), elastic moduli (bulk modulus
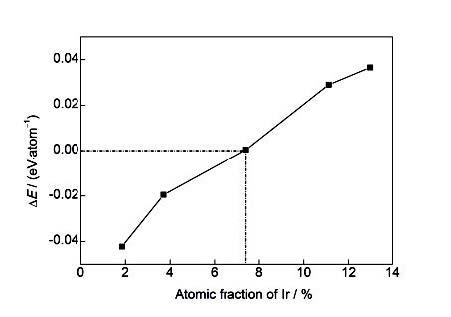
合金形成能主要用来衡量Ir元素对钨合金相稳定性的影响,结果示于图2。可以看出,随着Ir含量的增加,W-Ir合金的形成能为负,但是呈现增加趋势;当Ir的添加量大于约7.4%时,W-Ir合金的形成能由负转正,预示着当Ir添加量大于7.4%时会有损W基体材料的相稳定性。Ir诱发的W-Ir合金基态相不稳定的物理根源将在随后的电子结构分析部分揭示。
图2 W-Ir二元合金形成能(ΔE)与Ir添加量的变化关系
Fig.2 Variation of formation energy (ΔE) of W-Ir binary alloys changes with Ir addition
图3给出了W-Ir合金的晶格常数随着Ir的添加量变化的情况。可以看到,随着Ir含量的增加,W-Ir合金的晶格常数单调减小。引起这种晶格常数变化的原因在于Ir的原子半径(0.136 nm)小于W的原子半径(0.141 nm)。
图3 W-Ir二元合金的晶格常数与Ir含量的关系
Fig.3 Relationship between a and Ir content for W-Ir binary alloys
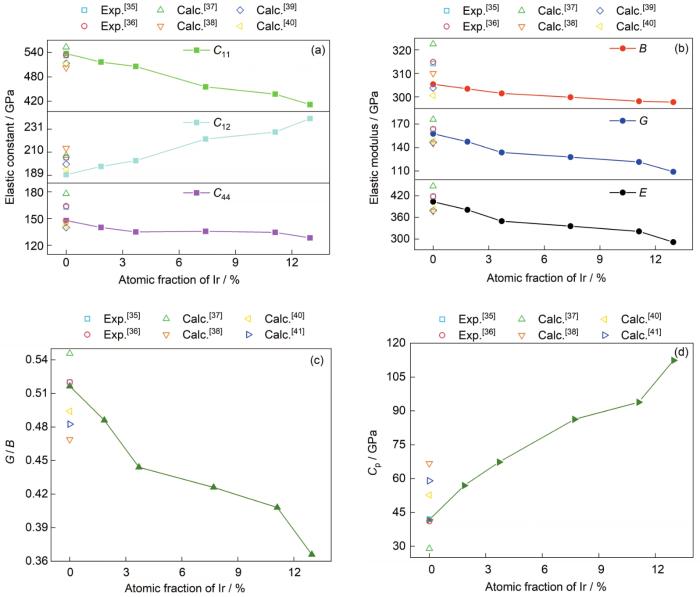
W-Ir二元合金和纯W[35~41]的弹性常数(C11、C12、C44)、弹性模量(B、G、E)、G / B和Cp随Ir添加量的变化曲线示于图4。可以看到,纯W计算值均在其他实验和计算所得结果范围之内,表明了当前弹性系数计算方法和参数设置的可靠性。弹性系数C11表征了晶体材料在承受单轴应变时的抗变形能力,C12和C44则分别表征了晶体材料沿着(00l) (l为晶面指数)侧面和<111>四度轴向的抗剪切能力。图4表明,随着Ir含量的增加,C11和C44呈减小趋势,表明Ir的加入可以明显降低单轴受力和<111>轴向剪切时的抗变形能力,提升材料韧性;而C12则随Ir含量增加而单调增加,表明合金抗平面剪切变形能力增加,预示该方向变形时材料刚度增加;弹性模量B、G和E均随着Ir的添加单调递减,表明Ir的添加会降低材料发生体积变形、剪切变形和单轴变形时的抗变形能力。这一结果预示W-Ir合金在遭受外部应力时,W-Ir合金体系比纯W体系更易达到剪切应力极限诱发位错发射,通过塑性协变缓解裂纹尖端应力集中,稳定了裂纹尖端(韧性特征),避免或者延缓了脆性断裂。这种Ir诱发的易变形特性也从另一个角度验证了图2中形成能的计算结果,即Ir能诱发相的不稳定特性。随着Ir含量从0增加到12.96%,表征韧脆特征的参量G / B从0.52 (脆性)降低到0.37 (韧性);Cp为正值,且随着Ir含量的增加从42 GPa增加到112 GPa,也预示着Ir的添加能改善W基体的脆性,提升其韧性[18]。这一结论与Luo等[8,9]和McKamey等[10]的实验观察一致。该实验研究发现,Ir的加入会导致钨合金的极限拉伸应力和屈服强度下降,韧性增加。另外,对比Ir和Mo在W中的韧化效果,Mo含量从0变化至70%,G / B仅降低0.03[49],而Ir含量从0变化到12.96%,G / B降低0.15,可见Ir对W的韧化效果远远大于Mo对W的韧化作用。本工作将进一步从电子价键的角度去分析其韧化机理。
图4 W-Ir二元合金和纯W[35~41]的弹性常数(C11、C12、C44)、弹性模量(B、G、E)、G / B和Cp随Ir添加量的变化曲线
Fig.4 Variations of elastic constants (C11, C12, C44) (a), elastic moduli (B, G, E) (b), G / B (c), and Cp (d) with Ir additions for W-Ir binary alloys (The corresponding data of bcc-W from literatures [35-41]are also presented for comparison)
虽然整体上Ir对W的合金化作用呈现韧性,但是W-Ir合金的平面剪切强化特性不可忽略,需慎重考虑特殊服役环境下的应力发展情况。尤其是当晶体结构具有大量明显的特征取向(如织构)时,要尽量避免外力加载方向与(00l)方向平行,此时W-Ir合金易发生脆性形变。
图5 不同W-Ir合金中Ir与第一近邻W原子所成的Ir—W1键以及Ir与第二近邻W原子所成的Ir—W2键的投影晶体轨道Hamilton布局(pCOHP)曲线
(a) W98.15Ir1.85 (b) W96.30Ir3.70 (c) W87.04Ir12.96
Fig.5 Relationships between energy and projected crystal orbital Hamiltonian population (pCOHP) for different W-Ir alloys (Ir—W1 (Ir—W2) refers to the bonding between Ir and its 1st (2nd) nearest neighbor W atoms)
图6 不同W-Ir二元合金的平面及三维差分电荷密度分布
Color online
(a) W98.15Ir1.85, (
(c) W87.04Ir12.96, (
Fig.6 Differential charge densities of different W-Ir binary alloys
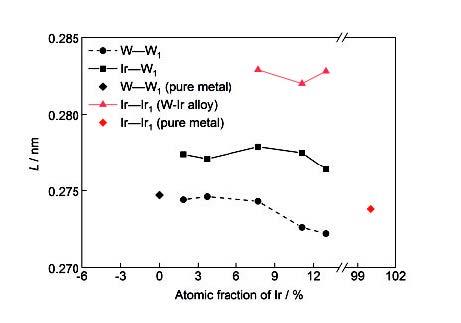
图7 W-Ir合金的第一近邻原子间(W—W1、Ir—Ir1、Ir—W1)平均键长以及纯金属Ir和W的第一近邻原子间(Ir—Ir1和W—W1)平均键长
Fig.7 Average bonding lengths between the first neighbor atorns (L) of W—W1, Ir—W1, and Ir—Ir1 for different W-Ir binary alloys, and Ir—Ir1 and W—W1 for pure metal
pCOHP曲线中,横轴左侧(负值)表示反键态,右侧(正值)表示成键态,纵轴表示轨道电子占据能级。Ir和第一近邻W原子间的pCOHP价键(Ir—W1)分析表明,轨道电子中的反键态部分地占据了Fermi能级以下区域,因此降低了W的相稳定性;在Fermi能级以下区域,Ir—W键的成键电子呈非局域化分布,表明其价键类型为金属键;随着Ir含量增加,Ir—W1成键区域峰值增加,预示Ir—W键作用增强;Ir—W2键因为距离较远其强度变化不明显。但Ir含量较高时(图5c),有少量反键态电子出现在Fermi能级,同时成键态电子向Fermi能级方向扩展,预示合金元素间的价键活性增加,稳定性降低。W—Ir价键的不稳定特征揭示了图2中Ir含量增加导致W-Ir合金形成能增加,相稳定性降低,以及图4b中W-Ir合金剪切模量降低,韧性得到改善的物理根源。
W—Ir之间的键强表征于平面差分电荷图(图6a~c)中2个原子之间。随着Ir含量从1.85%增加到3.7%、12.96%,相应的键强最大值由2.247增加到2.309、2.582,这一结果与pCOHP曲线中价键分析一致。另外,W—Ir1之间的电荷增强区域在垂直于<111>的方向有所拉长,引起了各个近邻W1原子之间键强增加。这种方向性价键的增强预示着W-Ir合金在相应方向上的强度较纯W有所增加,与平面抗剪切变形能力(C12)的增加相关。
从图7中可以看出,Ir添加到钨基合金中以后,Ir—W1和W—W1键长均随着Ir含量的增加呈减小趋势,而Ir—Ir1间距较纯金属中的距离有了较为明显的增加。结合图5和6,本征脆性的Ir在W中的合金化作用可以总结为:(1) 对Ir元素而言,Ir原子的成键能级由纯金属态的高能级转变到W-Ir合金中的较低能级,稳定性增加;同时Ir—Ir原子间距拉长,纯金属Ir-Ir原子间的本征脆性在W-Ir合金中得以改善;(2) 对W基体而言,Ir的加入强化了W基体中的W—W以及Ir—W金属键作用,其中方向性的增强导致其抗平面剪切能力的增加;同时略微提升了W原子的成键能级,降低了W本身的相结构稳定性(本征脆性),韧性得到改善。
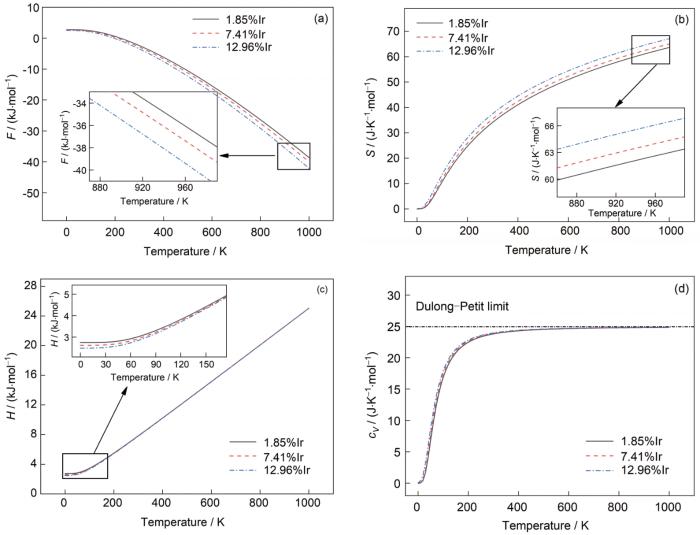
不同W-Ir合金的热力学性能示于图8。可以看出,随着温度升高,W-Ir合金的Helmholtz自由能降低,预示W和Ir之间易于自发形成固溶合金(图8a);晶体内部微观粒子振动加剧,混乱度增加,因此熵增加(图8b);在较低温度(0~150℃)范围内,W-Ir固溶体的焓随温度的增加变化很小,但温度进一步升高,焓明显增加(图8c),进一步表明W和Ir之间自发形成固溶合金的趋势随温度的升高而加强,合金稳定性随之增加,因此Ir适合作为W的高温强韧化元素。图8d显示了W1 - x Ir x 合金的比热容在低温阶段快速增加,随着温度进一步升高,增速变缓,接近Dulong-Petit极限,符合常规比热容变化规律,也表明热力学计算的可靠性。进一步分析Ir的成分变化对上述热力学参量的影响发现:同一温度下,W-Ir固溶体的自由能对Ir含量敏感性增加(图8a),Ir含量增加,自由能越低,W和Ir之间固溶的自发性越强,表明W-Ir固溶体的相互作用键能随Ir含量的增加而加强,热稳定性增强;Ir含量增加,体系的成分混乱程度增大,熵增加(图8b)。随着温度的升高,W-Ir固溶体的形成焓对Ir含量敏感性降低,趋于一致,这与W-Ir合金在当前所关注的温度范围内,热膨胀系数小,体积变化小有关(图8c)。
图8 不同W-Ir二元合金的自由能(F)、熵(S)、焓(H)和比热容(
Fig.8 Temperature dependences of free energy (F) (a), entropy (S) (b), enthalpy
(1) W-Ir合金的相稳定特性随着Ir含量的增加而逐渐降低,这与W—Ir价键中部分反键态占据Fermi能级以下区域有关;Ir在W中的添加量小于7.4%时,W-Ir合金满足基态相稳定条件。
(2) Ir的添加能降低晶格常数,这与Ir具有比W更小的原子半径有关。
(3) Ir的添加能明显改善W的韧性,同时提升了其抗平面剪切应变的强度,这与W—Ir价键的方向性增强有关。
(4) Ir的添加能提升W的热力学稳定性,温度越高,添加量越多,稳定性提升越显著。
(5) 本征脆性的Ir能韧化W的原因在于:Ir和W原子轨道发生作用时,其电子能级分布发生了明显变化,Ir中成键电子从纯金属Ir时高能级的
1 模型和方法
1.1 计算模型
图1
1.2 性能计算
1.2.1 形成能
1.2.2 弹性模量
1.2.3 热力学性质
1.2.4 W—Ir价键作用
1.3 参数设置
2 结果与分析
2.1 可行性验证
Element
Source
a / nm
B / GPa
G / GPa
E / GPa
G / B
Cp / GPa
W
Present
0.3171
305
158
404
0.52
41.71
Exp.
0.3165[33], 0.3166[34]
314[35], 315[36]
163[35], 164[36]
418[35], 419[36]
0.52[35], 0.52[36]
41.82[35], 41.79[36]
Calc.
0.3171[37]
323[37], 310[38],
176[37], 145[38],
447[37], 377[38],
0.55[37], 0.47[38],
29[37], 66.70[38],
304[39], 301[40]
147[39], 148[40]
379[39], 382[40]
0.49[40], 0.48[41]
52.7[40], 59[41]
Ir
Present
0.3877
342
226
555
0.66
-39.07
Exp.
0.3839[42]
363[43], 353[44]
221[43], 217[44]
550[43], 540[44]
0.61[43], 0.61[44]
-13[43], -14[44]
Calc.
0.3871[45]
351[45], 364[46],
232[45], 223[46],
570[45], 555[46],
0.66[45], 0.61[46],
-43[45], -15[46],
405[47], 347[48]
288[47], 222[48]
698[47], 549[48]
0.71[47], 0.64[48]
-88[47], -29[48]
2.2 形成能
图2
2.3 晶格常数
图3

2.4 弹性力学性能
图4
2.5 电子结构
图5
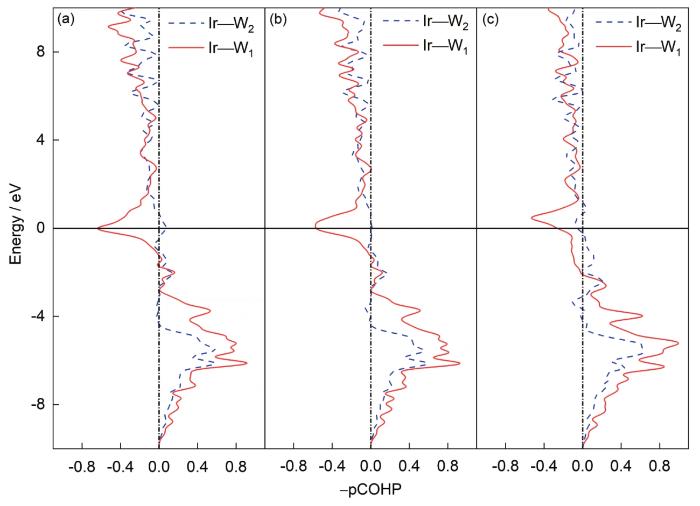
图6
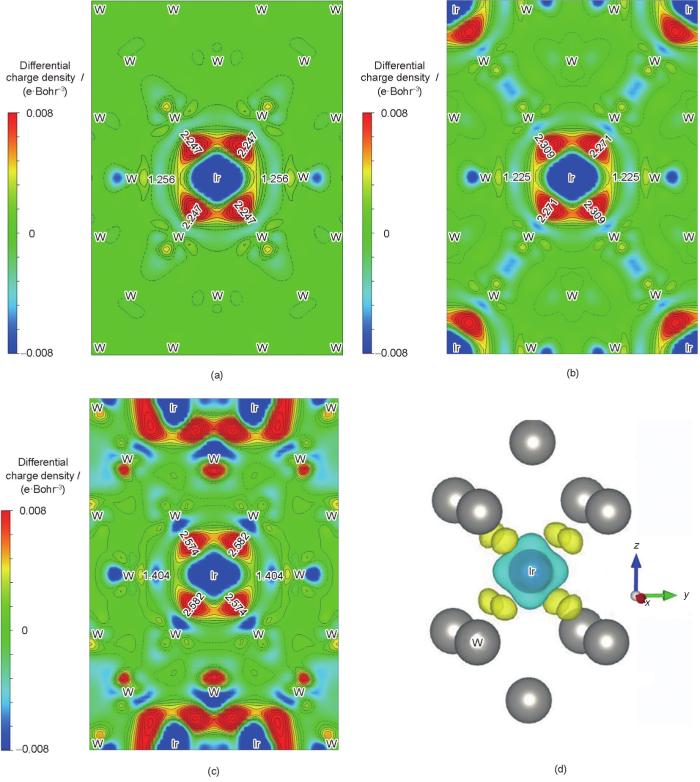
图7
2.6 热力学性能
图8
3 结论
来源--金属学报







 沪公网安备31011202020290号
沪公网安备31011202020290号
