当前位置：首页 » 国检检测新闻中心 » 检测百科 » 分享：孪生诱发软化与强化效应的Cu晶体塑性行为模拟

分享：孪生诱发软化与强化效应的Cu晶体塑性行为模拟

来源：国检检测查看手机网址

扫一扫!

扫一扫!

浏览：- 发布日期：2024-09-27 13:51:11【大中小】

郭祥如1,2, 申俊杰,1,2

1.天津理工大学天津市先进机电系统设计与智能控制重点实验室天津 300384

2.天津理工大学机电工程国家级实验教学示范中心天津 300384

摘要

基于晶体塑性理论，考虑孪生软化效应建立了描述孪晶形核、增殖和长大的位错密度基晶体塑性有限元模型。应用该模型揭示了不同晶体取向Cu单晶拉伸变形过程中位错滑移、孪生激活及其交互作用下的宏观塑性行为演化规律，进一步分析了Cu多晶拉伸变形过程中晶粒间交互作用对孪生软化、应变硬化等宏观塑性行为的影响。结果表明：孪生具有明显的取向效应，在孪生主导塑性条件下，Cu单晶塑性变形过程中孪晶增殖导致应力-应变曲线存在明显的应力突降现象，其塑性变形分为滑移、孪生及位错与孪晶交互作用3个阶段；此外，随着饱和孪晶体积分数增加，Cu单晶塑性变形过程中第3阶段的应变硬化率也随之提升。进一步模拟Cu多晶拉伸变形的塑性行为可知，在晶粒间交互作用下孪晶形核、增殖和长大过程中不会出现应力突降现象，与Cu单晶相比整个塑性变形过程具有更高的应变硬化率；Cu多晶塑性变形过程中位错密度在晶界处出现集中现象，孪晶也容易在晶界处形成。

关键词：晶体塑性 ; 孪生软化 ; 取向效应 ; 应变硬化 ; 塑性变形

众所周知，位错滑移和孪生是主导多种晶体材料(如孪生诱发塑性(TWIP)钢、Cu、Mg及其合金等)塑性行为的主要变形机制，孪晶激活演化及其与位错交互作用对晶体材料宏观塑性行为具有复杂影响。一方面，在孪生主导塑性条件下，孪晶激活演化过程中应力-应变曲线存在明显的应力突降现象，即孪生软化效应[1,2]。如Niewczas等[2]研究表明，在4.2 K条件下Cu单晶拉伸过程中力学响应曲线分为明显的滑移、孪生及位错与孪晶交互作用主导塑性3个阶段，在孪生主导塑性时发生应力突降现象；Seo等[3]在直径为40~250 nm的Au纳米线拉伸实验中发现，与孪晶形核相比，孪晶长大过程具有更低的临界应力。另一方面，孪晶阻碍位错运动使得晶体材料在塑性变形过程中表现出强化现象。如Cu单晶拉伸变形过程中的位错与孪晶交互作用阶段相比于滑移主导塑性阶段具有更高的应变硬化率[2]。然而，部分研究学者认为，晶体材料变形过程中孪晶对流动应力和应变硬化行为影响较小。如Liang等[4]采用实验方法表明，TWIP钢拉伸变形过程中孪晶对流动应力贡献不超过10%；Luo和Huang[5]采用实验研究表明，TWIP钢在无孪晶形成时也有较高的应变硬化率。目前上述实验表征中孪晶对宏观应力和应变硬化影响不同的原因尚未清晰。此外，实际工程应用中通常为多晶材料，与单晶不同的是，在描述多晶材料塑性变形的应力-应变曲线中尚未发现孪晶增殖相关的应力突降现象[6,7]。同时，受初始晶体取向、晶粒间交互作用等因素影响，多晶材料塑性变形过程中各晶粒形成孪晶时对应的应变不同，这使得孪晶激活软化效应及其与位错交互作用相关的强化效应共存，多晶材料塑性变形过程中多微观结构交互作用与宏观力学响应间的关联关系还不明确。

为了能够精确描述孪晶激活演化及其与位错交互作用对宏观塑性行为的影响，建立单晶和多晶材料塑性变形过程中微观机制演化与宏观塑性行为间的关联关系，考虑金属材料晶体结构和塑性变形特点的晶体塑性有限元(crystal plasticity finite element，CPFE)方法受到了学者们的广泛关注[8~13]。在晶体塑性理论描述孪生机制方面，Chin等[14]首先探索性地将孪生机制耦合至晶体塑性模型。Van Houtte[15]提出了孪生主导取向(predominant twin reorientation，PTR)方法。将孪生机制对晶体取向的影响进行了描述，当孪晶体积分数累计到阈值时，整个晶体转向孪生增量最大的方向。在此基础上，Choi等[16]对PTR方法进行修正，确定了孪晶转向的临界阈值。此外，Tomé等[17]提出了体积分数转换(volume fraction transfer，VFT)法，采用加权法将晶体取向耦合在自洽模型中，使晶体取向在每一个时间步结束之后进行更新。上述方法简化了孪生演化过程，根据微结构表征实验中孪晶区内不再发生孪生这一结果，Kalidindi[18]进一步提出了新的考虑孪生机制的晶体塑性理论基本框架，在塑性变形梯度中提出加权耦合孪生的速度梯度描述方法。近年来，在CPFE描述位错与孪晶交互作用方面，孙朝阳等[19,20]建立了耦合滑移和孪生机制的CPFE模型，描述了TWIP钢单晶变形过程中孪晶体积分数饱和引起孪生转向相关的软化效应和TWIP钢多晶拉伸过程中织构演化结果。为了更加直观地描述孪生软化效应，Beyerlein等[21]在CPFE模型中引入了不同的临界孪晶形核和长大应力来考虑孪生软化相关的应力突降现象。Wu等[22]进一步建立了描述孪晶形核、增殖和长大(twin nucleation, propagation and growth，TNPG)过程的黏弹塑性自洽模型，并在孪晶增殖过程中考虑了软化效应。Qiao等[23]在CPFE框架中引入了描述孪晶演化的TNPG模型，详细展示了孪晶增殖过程相关的软化效应。Wang等[24]采用耦合TNPG的黏弹塑性自洽模型揭示了外部加载条件对多晶材料宏观塑性行为的影响，研究表明，在应力加载和应变加载条件下分别形成应变突变和应力突降现象。然而，多晶条件下孪生软化效应及孪晶与位错间交互作用形成的强化效应等内部因素对宏观塑性行为影响还需进一步探索与确定。

本工作考虑孪生软化特点，基于晶体塑性理论建立描述孪晶形核、增殖和长大的位错密度基晶体塑性本构模型，基于ABAQUS/UMAT平台进行二次开发并进行数值实现。以Cu晶体为研究对象，建立Cu单晶拉伸过程的CPFE模型，研究不同取向Cu单晶变形过程中滑移和孪生激活及其交互作用下的宏观塑性演化行为，并揭示孪晶体积分数饱和值对宏观硬化行为的影响。进一步建立Cu多晶拉伸过程的CPFE模型，对比分析Cu单晶与多晶塑性变形过程中的硬化行为演化特点，研究揭示Cu多晶变形过程中晶粒间交互作用下的宏微观塑性行为演化规律。

1 耦合滑移和孪生机制的位错密度基晶体塑性模型

1.1 耦合孪生的变形运动学和动力学描述

晶体塑性理论认为，滑移是塑性变形的主要途径，晶体变形由位错滑移的塑性变形、晶格弹性变形和刚体转动共同完成。基于变形梯度的乘法分解，变形梯度( $?$ )分解为[18]：

? = ?_{e} \cdot ?_{p}

(1)

式中， $?_{e}$ 代表晶体弹性变形(晶格畸变)和刚性转动的合成， $?_{p}$ 代表晶体产生的塑性应变。

由式(1)可以得到速度梯度( $?$ )的表达式[18]：

? = \dot{?} \cdot ?^{- 1} =

{\dot{?}}_{e} \cdot {?_{e}}^{- 1} + ?_{e} \cdot {\dot{?}}_{p} \cdot {?_{p}}^{- 1} \cdot {?_{e}}^{- 1} = ?_{e} + ?_{p}

(2)

式中， $\dot{?}$ 、 ${\dot{?}}_{e}$ 和 ${\dot{?}}_{p}$ 分别表示对 $?$ 、 $?_{e}$ 和 $?_{p}$ 求导； $?^{- 1}$ 、 ${?_{e}}^{- 1}$ 和 ${?_{p}}^{- 1}$ 分别为 $?$ 、 $?_{e}$ 和 $?_{p}$ 的逆矩阵； $?_{e}$ 和 $?_{p}$ 分别表示弹性和塑性速度梯度。

考虑孪生机制对塑性行为的影响，将孪生引入速度梯度，则定义在初始构形上的塑性速度梯度( $?_{p, 0}$ )为[19]：

?_{p, 0} = {\dot{?}}_{p} \cdot {?_{p}}^{- 1} = \sum_{?} {\dot{?}}_{?} ?_{?} + \sum_{?} {\dot{?}}_{?} ?_{?} ?_{?}

(3)

式中，α和β分别为滑移系和孪生系的序号； ${\dot{?}}_{?}$ 为滑移系的塑性剪应变率； ${\dot{?}}_{?}$ 为孪晶体积分数变化率； $?_{?}$ 为孪生剪切量，为一常数(0.707)； $?_{?}$ 和 $?_{?}$ 则分别为滑移系和孪生系的Schmid张量，即：

?_{?} = ?_{?} \otimes ?_{?}

(4)

?_{?} = ?_{?} \otimes ?_{?}

(5)

式中， $?_{?}$ 和 $?_{?}$ 分别为第α个滑移系初始构形的滑移方向和滑移面法向， $?_{?}$ 和 $?_{?}$ 分别为第β个孪生系的孪生方向和孪晶面法向。

根据晶体塑性理论，弹性应变张量( $?_{e}$ )可由弹性变形梯度得到[25]：

?_{e} = \frac{1}{2} (?_{?}^{?} \cdot ?_{e} - ?)

(6)

式中， $?_{?}^{?}$ 为 $?_{e}$ 转置矩阵， $?$ 为单位张量。

其中，与 $?_{e}$ 共轭的第二Piola-Kirchhoff应力( $?_{e}$ )为[25]：

?_{e} = {?_{e}}^{- 1} \cdot \{d e t (?_{e}) ?\} \cdot {?_{e}}^{- T}

(7)

式中， $d e t (?_{e})$ 为 $?_{e}$ 的行列式； $?$ 为Cauchy应力； ${?_{e}}^{- T}$ 为 $?_{e}$ 转置后的逆矩阵。

当单晶体弹性应变较小时， $?_{e}$ 可以表述为应变的线性函数：

?_{e} = ? : ?_{e}

(8)

式中， $?$ 为4阶弹性张量，是一个材料常数矩阵。

根据Schmid定律，第α个滑移系或第β个孪生系的切应力 $?_{?}$ 或 $?_{?}$ 为：

?_{?} = ? : ?_{?}

(9)

?_{?} = ? : ?_{?}

(10)

基于黏塑性方法， ${\dot{?}}_{?}$ 可以表示为[18]：

{\dot{?}}_{?} = {\dot{?}}_{0, ?} {|\frac{?_{?}}{?_{?}}|}^{1 / ?} s i g n (?_{?})

(11)

式中，m为反映材料应变特性的率敏感系数； ${\dot{?}}_{0, ?}$ 为参考塑性剪应变率； $s i g n (?_{?})$ 为符号函数，当滑移系α上 $?_{?}$ 大于滑移阻力( $?_{?}$ )时，滑移系将启动。本模型中，孪生激活演化法则与滑移相同。

1.2 耦合滑移与孪生的硬化模式表征

根据Allain等[26]的工作，位错运动中第α个滑移系受到的 $?_{?}$ 可以表示为晶格摩擦力( $?_{0, ?}$ )与位错密度有关的位错间交互作用力之和：

?_{?} = ?_{0, ?} + ? ? \sqrt[]{\sum_{? = 1}^{12} ?_{? ?} ?_{?}}

(12)

式中，μ为剪切模量；b为位错Burgers矢量模； $?_{?}$ 为滑移系β的位错密度； $?_{? ?}$ 为12 × 12的矩阵系数，描述各滑移系位错间的相互阻碍作用[27]。

考虑位错增殖与湮灭对位错密度演化的影响，第 $?$ 滑移系的位错密度( $?_{?}$ )演化应变率可表示为[26]：

\frac{d ?_{?}}{d ?_{?}} = (\frac{1}{? ?_{?}} - ?_{r} ?_{?})

(13)

式中， $?_{?}$ 为第 $?$ 滑移系的剪应变； $?_{r}$ 为动态回复系数； $?_{?}$ 为第 $?$ 滑移系的位错平均自由程，考虑到晶体材料塑性变形过程中孪晶的产生，在位错密度演化中引入孪晶间距的影响， $?_{?}$ 表示为[26]：

\frac{1}{?_{?}} = \frac{1}{?} + \frac{1}{?_{α}} + ?_{f} \sqrt[]{?}

(14)

式中， $?$ 为有效晶粒尺寸； $?_{f}$ 表示林位错对位错运动的阻碍强度； $?_{?}$ 为孪晶片层间距，可表示为[26]：

\frac{1}{?_{?}} = \frac{?_{? ?}}{?_{?}}

(15)

式中， $?_{?}$ 为孪生系β中微孪晶片层间距， $?_{? ?}$ 表示孪晶对位错滑移的阻碍强度。当孪晶所在平面与位错滑移面平行时，孪晶对位错滑移无影响， $?_{? ?}$ = 0；当孪晶面与位错所在滑移面倾斜时， $?_{? ?}$ = 1。在多孪生系中孪晶平均间距与孪晶体积分数和孪晶片层厚度关系为[26]：

\frac{1}{?_{?}} = \frac{?_{?}}{2 ? (1 - ?)}

(16)

式中， $?$ 为平均孪晶片层厚度； $?_{?}$ 第 $?$ 孪生系生成的孪晶体积分数； $?$ 为全部孪晶体积分数。

1.3 孪晶形核、增殖和长大演化描述

针对孪生机制，孪晶形核后孪生位错快速滑过孪晶面进行增殖和长大，孪晶增殖过程中随孪晶体积分数增多临界孪生应力减少，这意味着临界孪晶形核应力大于孪晶长大应力。考虑孪晶增殖过程中的软化效应，根据Wu等[22]提出的TNPG模型中对孪晶形核、增殖和长大过程的描述，孪生阻力( $?_{?}$ )演化可用如下形式表示：

?_{?} = \{\begin{matrix} ?_{0, ?} - \frac{?_{0, ?} - ?_{g, ?}}{?_{g, ?}} ?_{?} (?_{?} \leq ?_{?, ?}) \\ \begin{array}{l} ?_{?, ?} + (?_{1, ?} + ?_{1, ?} ?) (1 - e x p (- \frac{?_{0, ?}}{?_{1, ?}} ?)) \\ (?_{?} > ?_{?, ?}) \end{array} \end{matrix}

(17)

式中， $?_{0, ?}$ 表示临界孪晶形核应力； $?_{1, ?}$ 为饱和孪生阻力与临界孪晶形核应力之差； $?_{g, ?}$ 为最小孪生阻力； $?_{g, ?}$ 为临界孪晶体积分数，表示孪晶增殖过程中所产生的孪晶体积； $?_{0, ?}$ 和 $?_{1, ?}$ 分别表示孪生初始硬化率和线性硬化率； $?$ 为全部滑移系和孪生系所累积的剪应变。

2 耦合孪生的Cu晶体塑性模型建立及实验验证

2.1 晶体塑性有限元模型建立

参考前期晶体材料塑性变形建模过程，将晶体塑性理论与有限元软件相结合，通过ABAQUS/UMAT平台二次开发，对晶体材料塑性变形过程中滑移和孪生激活演化下的宏观力学响应进行数值模拟[19,20]。本工作以Cu为研究对象，建立Cu单晶拉伸过程的有限元模型，如图1所示。选择一个立方体单元表示Cu单晶，并建立XYZ三维直角坐标系，单元类型为C3D8R (3维8节点缩减单元)，在坐标原点O施加固定约束，XOY平面上其他3个顶点施加Z方向的位移约束，在立方单元上表面沿Z方向施加位移载荷。结合Niewczas等[2]的Cu单晶拉伸实验结果，通过改变初始Euler角可实现Cu单晶沿不同取向的加载。

图1

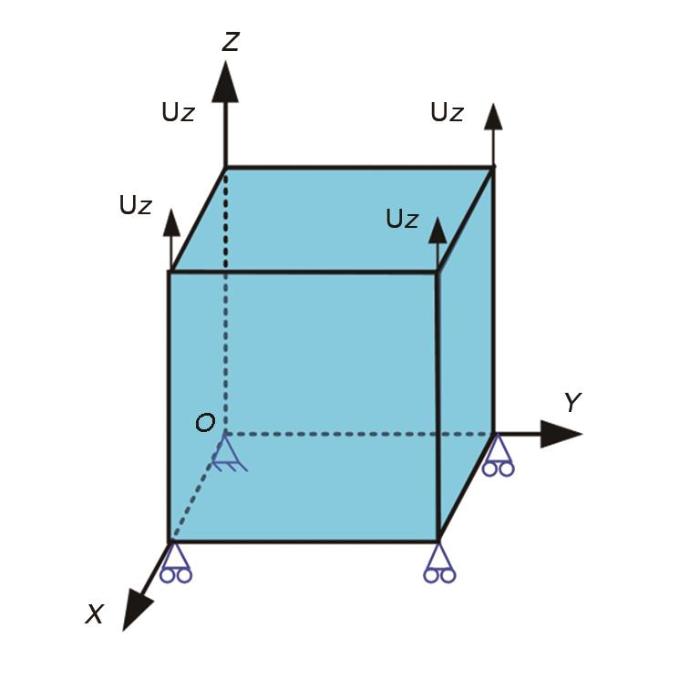
图1 Cu单晶拉伸过程的晶体塑性有限元模型示意图

Fig.1 Schematic of macroscopic tensile process for Cu single crystal by using crystal plastic finite element (CPFE) model (Uz—the tensile direction)

2.2 晶体塑性模型参数确定

为了应用该模型准确模拟材料的宏观力学响应及其微结构演化行为，必须确定该模型相关材料参数。结合fcc晶体材料滑移系和孪生系的晶体学特征，根据前人对Cu的研究结果[2,12,23,28~31]，并不断取一些试探值进行参数灵敏度分析修正模型中的材料参数，最终得到晶体塑性模型Cu单晶材料参数，如表1[2,23,28~31]所示。具体材料参数获取过程为：固定参数C11、C12、C44、 $?$ 和b来自文献[28]；CPFE模型中， ${\dot{?}}_{0}$ 、 $?$ 、 $?_{0}$ 、 $?_{0}$ 、 $?_{r}$ 和 $?_{f}$ 来自文献[29,30]；由文献[2,31]实验表征可知，孪晶体积分数饱和值( $?_{t}$ )取为0.7，D为3 mm， $?$ 为220 nm；此外，针对CPFE模型中引入的孪晶形核、增殖和长大演化公式中各参数，由Niewczas等[2]实验表征可知，孪晶形核时应力约为450 MPa，对应的 $?_{0, ?}$ 为150 MPa， $?_{1, ?}$ 为60 MPa，孪晶形核后应力突降值370 MPa，对应的 $?_{g, ?}$ 为110 MPa，同时， $?_{g, ?}$ 、 $?_{0, ?}$ 和 $?_{1, ?}$ 由文献[23]获得并进行适当调整。

表1 CPFE模型中Cu单晶材料参数[2,23,28~31]

Table 1 Material parameters in the CPFE model for Cu single crystal[2,23,28-31]

Parameter	Value	Unit
C11[28]	168	GPa
C12[28]	121	GPa
C44[28]	75	GPa
$?_{t}$ [2,31]	0.7
${\dot{?}}_{0}$ [29,30]	0.001	s-1
$?$ [29,30]	0.024
$?_{0}$ [29,30]	5	MPa
$?$ [28]	48	GPa
b[28]	0.025	nm
$?_{0}$ [29,30]	1012	m-2
$?_{r}$ [29,30]	6
$?_{f}$ [29,30]	0.3
$?$ [2,31]	220	nm
D[2,31]	3	mm
$?_{0, ?}$	150	MPa
$?_{1, ?}$	60	MPa
$?_{g, ?}$	110	MPa
$?_{g, ?}$ [23]	0.005
$?_{0, ?}$ [23]	70
$?_{1, ?}$ [23]	0

Note:C11, C12, and C44—elastic constant, $?_{t}$ —twin volume fraction saturation value, ${\dot{?}}_{0}$ —reference shear rate, $?$ —strain rate sensitivity, $?_{0}$ —lattice friction, $?$ —shear modulus, b—Burgers vector, $?_{0}$ —initial dislocation density, $?_{r}$ —dynamical recovery coefficient, $?_{f}$ —parameter related to the forest, $?$ —mean twin thickness, D—effective grain size, $?_{0, ?}$ and $?_{1, ?}$ —initial and back-extrapolated critical resolved shear stresses, respectively, $?_{g, ?}$ —the minimum twin resistance, $?_{g, ?}$ —critical twin volume fraction, $?_{0, ?}$ and $?_{1, ?}$ —the initial and the asymptotic hardening rates, respectively

新窗口打开| 下载CSV

2.3 模型验证

为了验证上述CPFE模型的可靠性，图2给出了Cu单晶沿不同取向拉伸过程的力学响应模拟及实验结果[2,28]的对比情况。其中[541]和[163]取向对应Euler角分别为(81°, 129°, 0°)和(171°, 64°, 9°)。可以看出，模拟结果与实验结果吻合良好。在Cu单晶沿[541]取向加载条件下，其应力-应变曲线分成明显的3个阶段，即滑移阶段A、孪生阶段B及位错与孪晶交互作用阶段C。阶段A内晶体塑性变形全部由位错滑移主导，随应变增加激活滑移系数量也相应增加，位错间交互作用增强，此时应变硬化由林位错主导；当加载应变为0.68时，Cu单晶变形过程中的孪生分切应力大于临界孪晶形核应力，此时进入B阶段。B阶段晶粒内孪晶形核并迅速增殖，同时伴随着流动应力急剧下降。在孪晶长大过程中，随着孪晶体积分数急剧增加，孪晶片层间交互作用增强，孪晶长大所需应力增加，该阶段内塑性变形几乎全部由孪生主导，在应变为0.84时孪晶体积分数达到饱和值，在后续变形过程中孪晶体积分数不再继续增加，晶体内的滑移系再次被激活，此时进入C阶段。C阶段晶粒内存在大量孪晶片层结构，孪晶将阻碍与孪晶面相倾斜滑移面上的位错运动，减少位错运动平均自由程，形成Hall-Petch强化效应，从而使其具有更高的应变硬化率。然而，在[163]取向加载条件下，应力-应变曲线中未出现应力突降现象，在整个塑性变形过程中未有孪晶形成，塑性变形全部由位错滑移主导。对比C阶段[541]取向和[163]取向下的应力-应变曲线可知，[541]取向下Cu单晶塑性变形过程中具有更高的应变硬化率，说明孪晶的形成对硬化行为具有积极作用。

图2

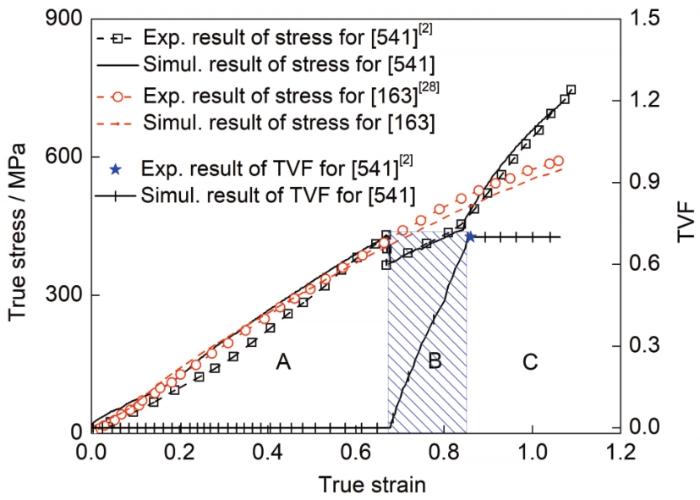
图2 Cu单晶沿[541]和[163]取向拉伸变形过程中真应力和孪晶体积分数随应变演化的模拟与实验[2,28]结果

Fig.2 Simulated and experimental[2,28] results of true stress and twin volume fraction (TVF) of Cu single crystal along [541] and [163] orientations, respectively

为了深入揭示Cu单晶塑性变形过程中各滑移系和孪生系激活演化行为及孪晶对位错滑移的影响，图3给出了[541]取向下Cu单晶拉伸变形过程中各滑移系和孪生系激活演化结果。可以看出，该取向加载下， $(\bar{1} \bar{1} 1) [0 \bar{1} \bar{1}]$ 和 $(\bar{1} \bar{1} 1) [101]$ 滑移系首先被激活来协调塑性变形，随着加载应力的提高， $(1 \bar{1} 1) [110]$ 和 $(\bar{1} 11) [\bar{1} \bar{1} 0]$ 滑移系也相应地被激活，塑性应变由多个滑移系共同主导。当应变大于0.68时，激活滑移系的塑性应变保持恒定(图3a中B区域)。由图3b可以看出，B阶段孪生系 $(\bar{1} 11) [211]$ 、 $(1 \bar{1} 1) [121]$ 和 $(\bar{1} \bar{1} 1) [112]$ 被激活，随着应变增加，3个孪生系产生的塑性应变急剧增加，对比图3a和b可知，B阶段塑性应变全部由孪生主导，位错滑移对塑性应变几乎无影响。当应变为0.84时，孪晶体积分数达到饱和值0.7，之后基体区内的 $(1 \bar{1} 1) [110]$ 及孪晶区内的 $(111) [\bar{1} 01]$ 和 $(111) [1 \bar{1} 0]$ 滑移系激活。此时，塑性变形又转变为由位错滑移主导。Niewczas等[2]的实验研究表明，C阶段的激活滑移面为 $(1 \bar{1} 1)$ 和 $(111)$ 面，这与模拟结果一致。同时，在位错与孪晶交互作用下，Cu单晶塑性变形过程具有更高的应变硬化率。通过对比模拟和实验结果[2,28]可知，CPFE模型在描述孪生软化效应及孪晶与位错交互作用相关的强化效应方面具有一定可靠性。

图3

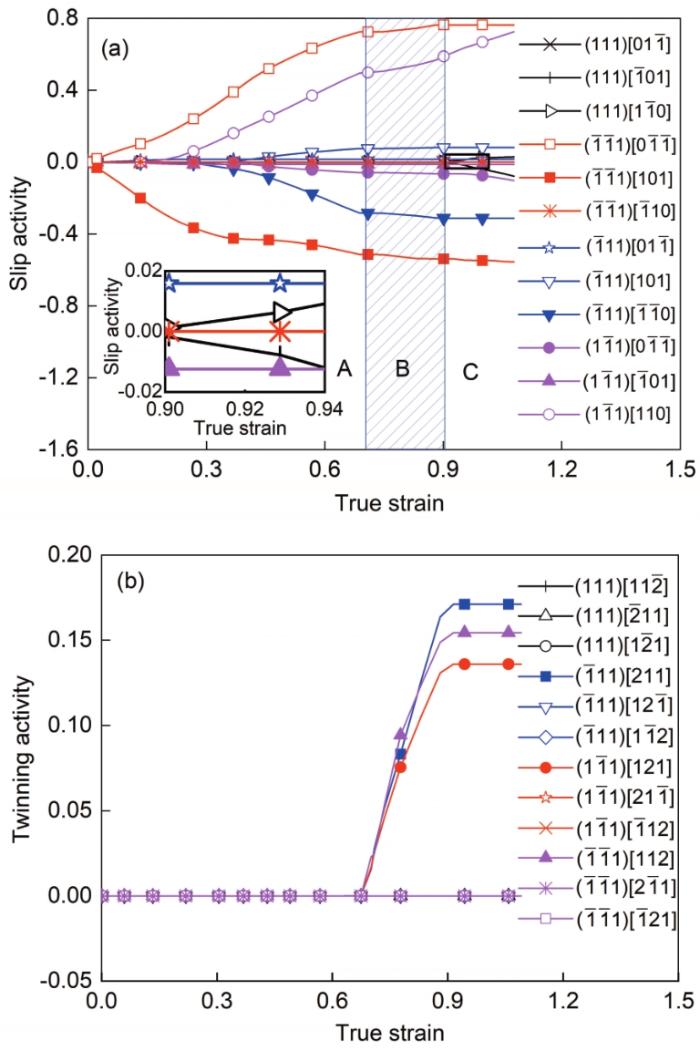
图3 Cu单晶沿[541]取向拉伸变形过程中各滑移系和孪生系的激活演化结果

Fig.3 Slip activities of slip systems (a) and twinning activities of twin systems (b) during the tension of Cu single crystal along the [541] orientation (The inset shows the enlarged view of the rectangle area in Fig.3a)

3 分析讨论

3.1 饱和孪晶体积分数对宏观塑性行为的影响

上述研究表明，晶体材料在塑性变形过程中形成的孪晶将阻碍位错运动，对应变硬化具有积极影响。而Liang等[4]采用实验研究表明，TWIP钢塑性变形过程中孪晶对流动应力和硬化行为的影响较小。对比实验研究结果发现，Cu单晶塑性变形过程中饱和孪晶体积分数为0.7[2]，远大于TWIP钢所产生的饱和孪晶体积分数0.2[4]。由此可知，饱和孪晶体积分数对晶体材料宏观力学响应具有重要影响。图4给出了不同饱和孪晶体积分数阈值Cu单晶沿[541]取向拉伸过程中真应力、应变硬化率和位错密度的演化结果。可以看出，在位错与孪晶交互作用的C阶段，随着饱和孪晶体积分数阈值增加，Cu单晶塑性变形过程中具有更高的流动应力、应变硬化率及位错密度。由于Liang等[4]实验材料饱和孪晶体积分数较低，因此TWIP钢塑性变形过程孪晶对宏观应力和应变硬化影响较小。

图4

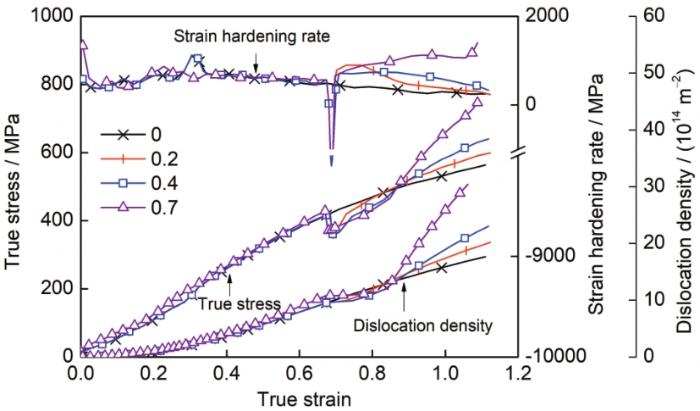
图4 [541]取向下不同饱和孪晶体积Cu单晶拉伸变形过程中真应力、应变硬化率和位错密度演化结果

Fig.4 Evolution curves of true stress, strain hardening rate, and dislocation density of Cu single crystal with different twin volume fraction saturation values along [541] orientation during tension

3.2 晶粒间交互作用对宏观塑性行为的影响

在实际工程应用中通常为多晶材料，其位错运动过程中除受到孪晶影响外，晶粒间交互作用将阻碍晶界处位错进一步运动。为了进一步对比分析晶体材料塑性变形过程中的孪生软化效应、位错与孪晶交互作用及晶粒间交互作用对宏观硬化行为的影响，基于已建立的Cu单晶拉伸变形的CPFE模型，进一步建立考虑不同初始晶粒取向的Cu多晶拉伸变形的有限元模型，材料参数与表1[2,23,28~31]中相一致。为了反映多晶中晶粒的组织形貌及取向特征，基于Voronoi的特征微元重构多晶微结构[32]，如图5所示。该几何模型由开源软件Neper建立，约包含100个等轴晶粒，本工作建立的多晶模型忽略初始织构的影响，假设其晶体取向随机且均匀分布，不同颜色代表不同晶体取向。基于建立的几何模型，将其划分为约12500个C3D4 (线性4面体)单元，约束方案与Cu单晶建模相一致，沿Z方向施加位移载荷。

图5

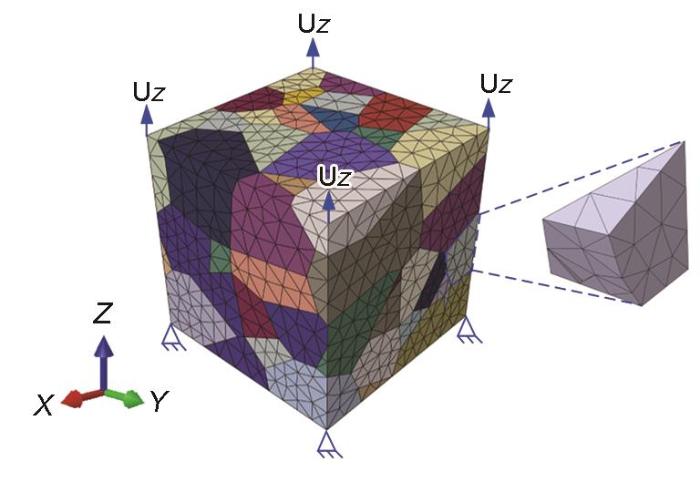
图5 Cu多晶拉伸过程晶体塑性有限元模型示意图

Fig.5 Schematic of macroscopic tensile process for Cu polycrystal by using CPFE model (The illustration on the right shows the morphology of a representative grain)

为了揭示多晶变形过程中孪晶对宏观力学响应的影响，图6给出了Cu多晶拉伸过程中宏观塑性行为的演化结果。可以看出，当Cu多晶中孪晶形成后，其应力增加速率变缓。当应变大于0.6时，孪晶体积分数增加速率逐渐缓慢，应力增加速率逐渐提升。同时，对比Cu单晶沿[541]取向的拉伸结果可知，在晶粒间交互作用下，Cu多晶拉伸过程中孪晶形成时未出现应力突降现象。为了进一步分析Cu多晶和单晶变形过程中孪生机制对应变硬化行为的影响，图7给出了Cu单晶和多晶拉伸变形过程的应变硬化率演化结果。对比Cu单晶沿[541]和[163]取向加载过程中的应变硬化率曲线可知，孪晶形成后将阻碍位错运动，导致其位错平均自由程急剧降低，位错密度急剧增加，从而使其具有更高的应变硬化率。由Cu单晶沿[541]取向加载过程中的应变硬化率演化曲线可知，随着孪晶的形成，应变硬化率出现突降后又突升现象；在应变大于0.84时，孪晶体积分数达到饱和值，在位错与孪晶交互作用下，Cu单晶塑性变形过程中的应变硬化率逐渐增加。当Cu多晶在塑性变形过程中形成孪晶时，其应变硬化率随应变增加逐渐下降，这是由孪生软化效应造成的；当应变为0.4~0.6时，其应变硬化率随应变增加逐渐上升，在该过程中，孪生软化效应、位错与孪晶间交互作用及晶粒间交互作用形成的强化效应共同主导硬化行为；当应变大于0.6时，Cu多晶变形过程中孪晶体积分数增加速率逐渐缓慢，此时硬化行为由位错与孪晶间交互作用及晶粒间交互作用共同主导。由此可知，晶粒间交互作用使得Cu多晶塑性变形过程中孪生软化相关的应变硬化率演化平滑，并具有更高的应变硬化率。

图6

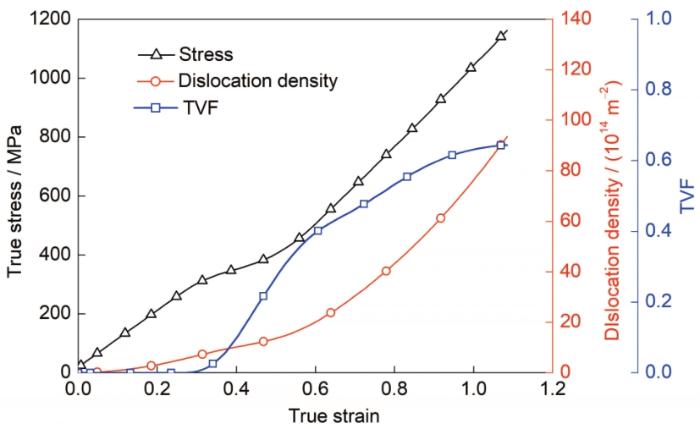
图6 Cu多晶拉伸变形过程中真应力、位错密度和孪晶体积分数随应变的演化曲线

Fig.6 Evolution curves of true stress, dislocation density, and TVF of Cu polycrystal during tension

图7

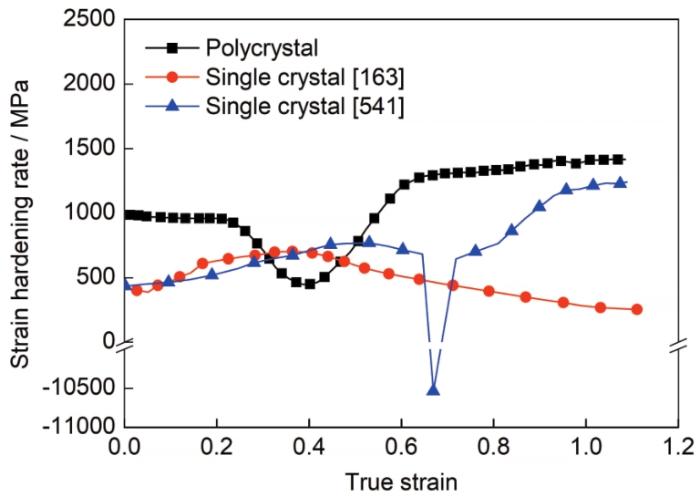
图7 不同取向Cu单晶和多晶变形过程中的应变硬化演化曲线

Fig.7 Evolution curves of strain hardening rate of Cu single crystal with different orientations and polycrystal during tension

为了直观反映位错滑移和孪生机制对Cu多晶变形过程中宏观塑性行为影响，图8 给出了Cu多晶加载结束时对应的位错密度和孪晶体分布结果。从整体分布情况可以看出，多晶内各晶粒具有的位错密度各不相同，晶粒存在非均匀塑性变形行为，这与各晶粒具有的晶体取向、晶粒形状及晶粒间交互作用等相关。从位错密度分布结果来看，多晶内高位错密度主要集中在晶界处，体现了晶粒间交互作用对硬化行为的积极影响。此外，由孪晶体积分布结果可知，Cu多晶变形过程中大部分晶粒内孪晶体积分数达到饱和值，仅部分晶粒内孪晶体积分数较低。为了进一步阐明如此多晶粒形成孪晶的原因，图9 给出了Cu多晶塑性变形过程中不同应变时对应的孪晶体积分布结果。由于孪晶具有明显的取向效应，在应变为0.32时，孪晶在某些特定取向晶粒的晶界处首先形成；随应变的增加，形成孪晶的晶粒数目逐渐增加，并逐渐达到饱和值；在应变为0.67时，存在某些晶粒内尚未形成孪晶的情况，说明该晶体取向下拉伸变形不利于孪晶的形成；随着应变进一步增加，晶粒间交互作用逐渐增强，在晶粒间交互作用下其他晶粒也逐渐形成孪晶，说明晶粒间交互作用促进不利取向晶粒内孪晶的形成。

图8

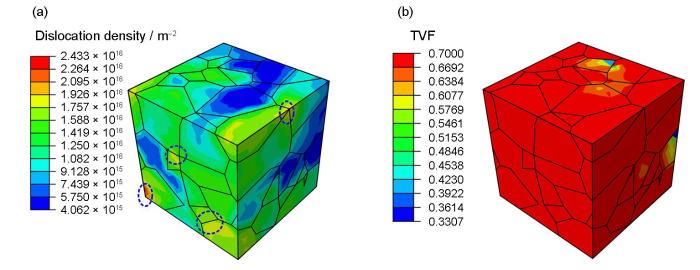
图8 多晶Cu拉伸变形后对应的位错密度和孪晶体积分布

Fig.8 Distribution maps of dislocation density (a) and TVF (b) of Cu polycrystal after tension (The dashed circles in Fig.8a mark the locations of dislocation density concentration)

图9

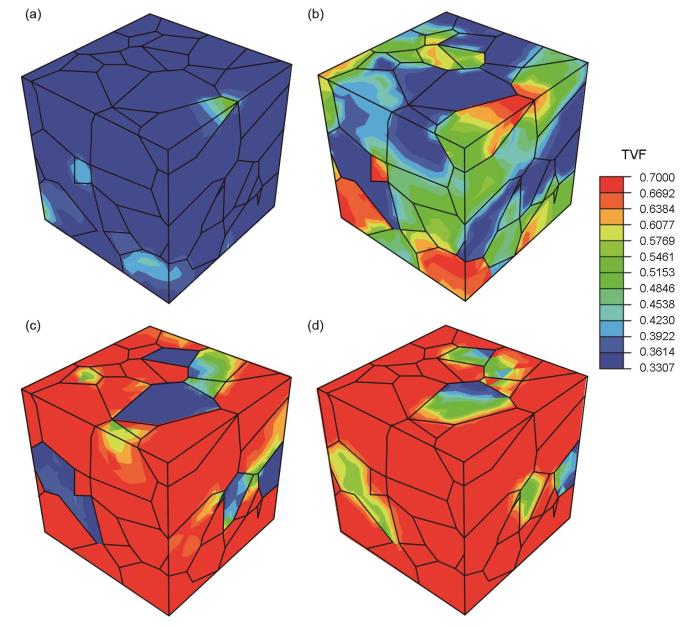
图9 多晶Cu拉伸变形过程中不同应变对应的孪晶体积分布

(a) ε = 0.32 (b) ε = 0.46 (c) ε = 0.67 (d) ε = 0.85

Fig.9 Distributions of TVF at different strains (ε) of Cu polycrystal during tension

4 结论

(1) 考虑了孪晶形核、增殖和长大过程中的应力突降现象，基于晶体塑性理论建立了耦合滑移和孪生机制的位错密度基晶体塑性有限元模型，应用该模型从细观尺度分别揭示了Cu单晶变形过程中孪生软化效应及孪晶与位错交互作用形成的强化效应对宏观塑性行为的影响。

(2) 孪生具有明显的取向效应，在孪生主导塑性条件下，Cu单晶塑性变形过程中孪晶增殖软化效应导致应力-应变曲线存在明显的应力突降现象，并将其塑性变形分为滑移、孪生及位错与孪晶交互作用3个阶段。孪晶与位错交互作用对宏观硬化行为具有积极影响，随着饱和孪晶体积分数增加，Cu单晶塑性变形过程第3阶段具有更高的应变硬化率；孪晶对应力和硬化行为影响随饱和孪晶体积分数增加而提升。

(3) 通过对Cu多晶拉伸变形过程模拟可知，在晶粒间交互作用下Cu多晶塑性变形过程中孪生软化相关应力和应变硬化率演化表现平滑，未出现单晶变形过程中的应力和应变硬化率突降现象，同时晶粒间交互作用使得Cu多晶塑性变形过程具有更高的应变硬化率。

(4) Cu多晶塑性变形过程中受晶体取向、晶粒形状及晶粒间交互作用等因素影响，各晶粒内位错密度分布不均匀，位错密度主要集中在晶界处。孪晶也首先在晶界处形成，随着应变增加，晶粒间交互作用逐渐增强，在晶粒间交互作用下不利于孪生取向的晶粒也逐渐形成孪晶。

下一篇：分享：上一篇：分享：稀土Ce对非调质钢中硫化物特征及微观组织的影响

“推荐阅读”

国检检测新闻中心 News Center