分享:尺寸因素对2D轴对称模型计算不锈钢管焊接残余应力精度的影响
采用数值模拟和实验相结合的方法研究了尺寸因素对2D轴对称模型计算SUS316不锈钢管焊接残余应力精度的影响。基于通用有限元软件MSC. Marc,分别采用2D轴对称模型和3D模型计算了不同尺寸圆管对接接头的温度场和焊接残余应力分布,并将小尺寸管残余应力计算结果与实验测量结果进行了比较。结果表明,2D轴对称模型与3D模型计算结果整体吻合较好,但在靠近内表面的焊缝及近焊缝区域,焊接残余应力的幅值和拉压应力区域的大小存在一定差别,且差别随圆管尺寸的增加而增大。对于实际的工程应用,在不考虑始终端应力问题时,可以用2D轴对称模型代替3D模型计算环焊缝稳定区残余应力,从而节省大量计算时间。
关键词:
奥氏体不锈钢具有良好的综合力学性能和优异的耐腐蚀性能,通过焊接等方式被用于制造反应堆堆芯区域结构件和蒸汽发生器传热管[1,2]。核电机组服役时,奥氏体不锈钢零部件在高温、高压环境和复杂载荷作用下,易出现应力腐蚀裂纹[3,4]。以往的研究[5]表明,核电设备中的应力腐蚀开裂问题通常出现在焊接热影响区附近。目前奥氏体不锈钢的应力腐蚀裂纹形成机理尚未完全阐明,但拉伸应力、腐蚀介质和材料敏化被认为是影响应力腐蚀裂纹的三大要因[6,7,8]。由于焊后不可避免地会在焊缝及热影响区产生残余应力,并且其峰值通常大于母材金属和焊缝金属的屈服强度,因此焊接残余应力的研究对于核电机组结构安全评估有重要的意义[9]。
目前测量焊接残余应力的实验方法存在诸多问题,如测量周期长、工作量大、成本高、有些方法可能会对构件造成损伤,因而在实际工程中应用受限。近年来,随着计算机技术的快速发展和计算焊接力学理论的日臻完善,有限元模拟方法已经成为预测焊接残余应力的有效工具[10,11]。然而焊接残余应力的计算是一个多场耦合且高度非线性的复杂过程,仍存在一些关键问题亟待解决,比如高速化计算方法的开发和高精度材料模型的建立[12]。目前常用的高速化计算方法有维数降低法、固有应变法和焊道合并法[13,14,15]。其中维数降低法的思想是将实际焊接问题简化为2D模型计算,从而降低计算模型的单元数和节点数,极大地提高计算效率[13]。Jiang等[16]研究了2D轴对称模型与3D模型计算焊接残余应力的差异,发现2种模型均能得到与实验结果吻合较好的应力峰值和分布趋势,其中3D模型计算结果与实验测试结果更为接近。Deng和Murakawa[17]比较了2D轴对称模型和3D模型计算的小尺寸圆管环焊缝的残余应力分布,研究表明,不考虑始终端位置时,3D模型计算稳定区的残余应力分布随圆心角位置的变化不明显,且与2D轴对称模型计算结果吻合较好,因而可以用2D轴对称模型代替3D模型计算环焊缝稳定区残余应力。上述研究表明,对于小尺寸圆管,由于结构刚度较小,此时2D轴对称模型计算的焊接残余应力结果与实验结果基本一致。然而到目前为止,尺寸因素(如圆管直径和管壁厚度)对2D轴对称模型计算焊接残余应力精度的影响还鲜有研究。如果能够澄清这一问题,将为大型焊接结构件的高速化计算提供理论依据。
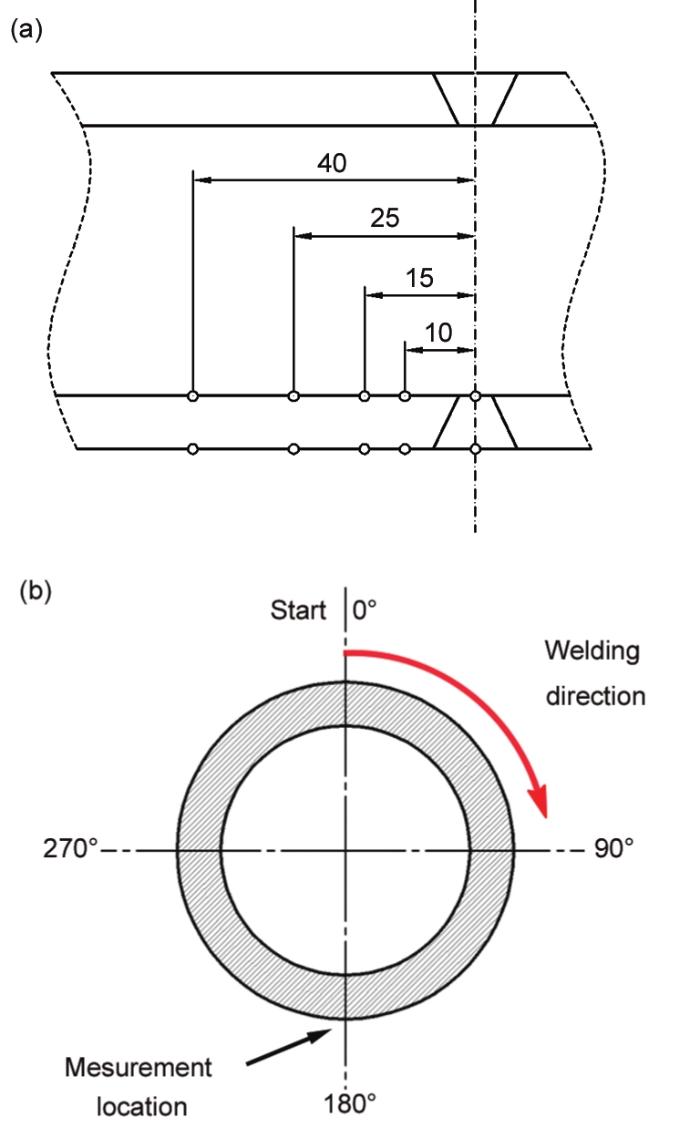
图1 坡口尺寸和焊道布置示意图
Fig.1 Schematic of weld groove dimension and welding sequence (unit: mm)
本工作以SUS316不锈钢管对接接头为研究对象,基于通用有限元软件MSC. Marc,分别采用2D轴对称模型和3D模型计算了SUS316不锈钢管对接接头的温度场和焊接残余应力,并通过小尺寸圆管模型计算结果与实验测量结果的比较对2D轴对称模型的有效性进行了验证。此外利用数值模拟的方法,研究了尺寸因素对SUS316不锈钢管环焊缝残余应力的影响,重点讨论了2D轴对称模型计算大尺寸圆管模型残余应力的适用性。
实验所用材料为SUS316奥氏体不锈钢,其主要化学成分(质量分数,%)为:C 0.08,Si 1.00,Mn 2.00,P<0.035,S<0.03,Ni 12,Cr 18.5,Mo 2.0,Fe余量。焊接接头的坡口尺寸和焊道布置如图1所示。采用钨极氩弧焊(TIG)进行焊接,焊接条件如下:每道焊道的线能量为0.4~1.0 kJ/mm,焊接速率为120 mm/min;层间温度低于150 ℃;保护气体为纯Ar;焊接填充材料采用Y316焊丝,其主要化学成分(质量分数,%)为:C 0.04,Si 0.33,Mn 1.88,P<0.019,S<0.002,Ni 12.7,Cr 19.3,Mo 2.26,Fe余量。计算焊接温度场和残余应力所考虑的焊接条件(焊接线能量、焊接速率和层间温度)与实验一致。
焊接完成后,采用应力释放法[18]测量残余应力。测量点分布在圆管180°截面的内外壁上,如图2所示。残余应力测量结果来自参考文献[19]。
图2 残余应力测量位置和焊接方向示意图
Fig.2 Schematics of residual stress measurement location (a) and welding direction (b) (unit: mm)
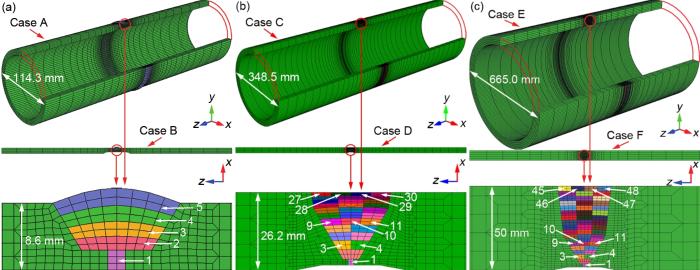
为了研究尺寸因素对SUS316不锈钢管焊接残余应力的影响,建立了如图3所示的有限元模型。在计算中定义了焊道和焊接顺序模拟实际焊接过程,并采用生死单元技术来考虑焊缝成形。为平衡计算精度和计算效率问题,在焊缝及其附近区域有限元网格划分得较密,而在远离焊接区域网格划分得相对稀疏。本研究中的有限元模型单元类型为Marc软件[20]中的八节点7号单元(3D FEM)和四节点10号单元(2D FEM)。实验中没有采用任何外部拘束,因此在有限元计算过程中采用的拘束条件仅用于防止模型发生刚性位移[21]。本研究共设立了6个计算案例(Case),见表1。其中Case A和Case B的模型尺寸与实验圆管一致,所有Case的圆管外径与管壁厚度的比值(d/t)均为13.3。
图3 3种不同尺寸圆管的2D和3D有限元模型
Fig.3 2D and 3D finite element (FE) models of thin pipe (a), middle pipe (b) and thick pipe (c)
Color online
表1 3种不同尺寸圆管的2D和3D有限元计算案例
Table 1
焊接过程中,电弧热在工件中热传导的控制方程为:
式中,T为温度;λ为热传导系数;qv为内部热源的发热功率;ρ为密度;c为比热容;t为传热时间;x、y和z为全体坐标系(x, y, z)中的坐标。
在3D模型的温度场计算过程中,采用Goldak等[22]提出的双椭球移动热源来模拟焊接热量输入。热源模型的前半部分与后半部分的热流密度可以用方程(2)和(3)描述:
式中,q1、q2为双椭球热源前半部分与后半部分的热流密度;Q=ηUI,为焊接热量(其中,U为焊接电压,I为焊接电流,η为焊接热效率,取η=0.75[23]);a1、a2、b、c为椭球形状参数;f1、f2为前后椭球热量分布函数,且f1+f2=2,在本研究中,取f1=0.6,f2=1.4[17]。
假设有限元模型所处坐标系为全体坐标系(x, y, z),则热源的坐标系相对于有限元模型而言是移动的。本研究采用局部坐标系(x', y', z')描述移动热源模型,满足:
式中,vx、vy、vz分别为热源在x、y、z方向上的速率分量。
2D轴对称模型中的焊接热输入用瞬间热源[9]来模拟。该热源模型中的热流密度分布均匀,包含2个重要参数:热源的热流密度(q)和加热时间(th),在保证每条焊道的总热量不变的情况下,通过调整这2个参数,使得焊接熔池的最高温度控制在1600~2000 ℃的范围。瞬间热源的热流密度可以用方程(7)描述:
式中,L为整条焊缝的长度,v为焊接速率,V为焊缝的体积。
由于工件在焊接过程中不仅要吸收来自电弧和金属熔滴的热量,还要向周围环境散热,因此在有限元模型中通过定义散热面考虑工件与外部环境的热量交换。本研究只考虑对流散热和辐射散热2种热损失形式,分别通过Newton定律(式(8))和Stefan-Boltzmann定律(式(9))描述:
式中,qc、qr分别为工件与周围环境之间的对流散热和辐射散热;hc为对流交换系数,取值为15×10-6 W/(mm2·℃);T0为环境温度(20 ℃);εr为热辐射系数,本次计算取εr=0.8;σr为Stefan-Boltzman常数。
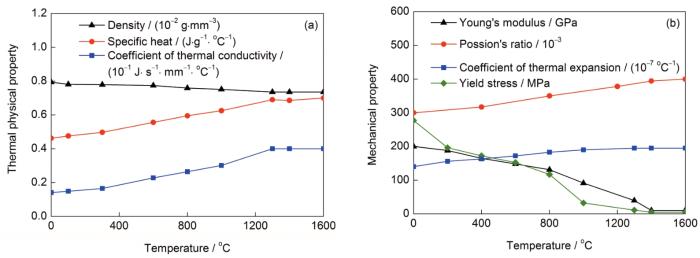
计算时,假设焊缝金属与母材具有相同的材料属性,材料的热物理性能参数[24]如图4a所示。
图4 材料热物理性能参数和力学性能参数
Fig.4 Thermal physical properties (a) and mechanical properties (b) of material
在力学模型中,采用与热分析时完全相同的网格模型,以温度场的计算结果作为热载荷加载到弹-塑性有限元模型中进行焊接残余应力和变形的计算。由于实验所用的材料为奥氏体不锈钢,不需考虑相变应变成分。同时,焊接过程中材料升温后在高温停留时间较短,蠕变现象也不明显,这样蠕变应变成分也可以忽略不计。因此,在奥氏体钢焊接过程中,材料的总应变(εtotal)可以用下式来描述:
式中,εe为弹性应变,εp为塑性应变,εth为热应变。
弹性应变计算遵循各向同性Hookean定律,对于塑性变形的计算采用了Von-Mises准则。材料加工硬化性能通过各向同性准则来描述,SUS316不锈钢的加工硬化系数参见文献[24]。同时采用了一种“阶跃式”退火模型来考虑退火软化效应的影响[12],退火软化温度设置为800 ℃[25]。材料的力学性能参数[24]如图4b所示。
为了便于定量比较温度场计算结果,在每种尺寸3D模型的180°截面上分别选取3个点(Point 1,Point 2和Point 3)来考察最后一道焊的热循环;同时,在对应的2D轴对称模型中,也同样选取对应位置的3个点来考察最后焊道的热循环。采用3D模型和2D模型计算得到的3个位置热循环的比较如图5所示。从此图可以看出,对于3种不同尺寸的圆管,2D轴对称模型与3D模型计算得到的各点峰值温度总体上吻合较好。但是在冷却阶段,2D轴对称模型计算得到各点的冷却速率要略大于3D模型的计算结果。这是因为3D模型在计算时采用了双椭球移动热源,可以模拟焊接电弧在空间中的移动过程和工件内部3个方向的热传导,而2D轴对称模型无法反映沿焊接方向(周向)的热传导,导致冷却阶段计算的温度下降速率偏大。在最后一道焊的外表面中心位置(Point 1),3D模型计算得到的峰值温度比2D轴对称模型的略高一些,但其它2个点的峰值温度几乎没有差别。由于本研究中所使用的材料是SUS316奥氏体不锈钢,计算过程中不需要考虑固态相变的问题,从力学模型的控制方程上分析可知,冷却速率的较小差异对后续残余应力场的计算结果不会造成显著影响。整体上看,2D轴对称模型计算的热循环曲线与3D模型计算结果比较吻合,而且尺寸因素对2D轴对称模型计算温度场精度影响也比较小,这一结果既验证了所使用的瞬间热源的有效性,也验证了2D轴对称模型计算不锈钢焊接接头温度场的有效性。
图5 不同尺寸圆管最后一道焊的热循环曲线
Fig.5 Thermal cycles during the last welding of thin pipe (a), middle pipe (b) and thick pipe (c)
Color online
图6对比了小尺寸圆管 Case A 180°截面和Case B的内表面与外表面的轴向残余应力分布以及实验测量[19]结果。从图6a可以看出,2D轴对称模型模拟得到的内表面上的轴向残余应力分布与3D模型的计算结果几乎一致,仅仅在焊缝内部表面附近3D模型得到的轴向应力峰值略高于2D模型的计算结果。总体上而言,2D轴对称模型和3D模型的计算结果与实验测量结果在分布和大小上都十分吻合。从图6b同样可以看到,2种有限元模型计算得到的外表面轴向残余应力分布也与测量结果吻合良好。但是,在焊缝中心和离焊缝中心约40 mm的位置,实验测量结果与数值模拟结果存在一定差异。由于焊接后贴应变片时,焊缝表面要进行处理(如机械打磨),相比较其它位置,焊缝表面更加粗糙而且不平,因此打磨掉的金属更多,这种处理会使焊缝表层金属产生一定的塑性变形而对焊态下产生的应力有一定的影响,这可能是导致焊缝区域的轴向残余应力测量值与计算存在一定差异的主要原因。对于离焊缝中心约40 mm的位置,焊前钢管经历了塑性加工而产生了加工硬化使得材料的屈服极限提高,而该处焊接热循环峰值温度会超过材料的屈服温度[26],但远低于退火温度,因此容易产生较大的残余应力。此外,由于该位置在焊接过程中峰值温度并不太高(220 ℃),因此焊接前的初期残余应力会部分或全部保留下来[17],初期的残余应力也是导致计算结果与实验结果差异的一个原因。
图6 内表面和外表面轴向残余应力的模拟结果与测量值[19]对比
Fig.6 Comparisons of axial residual stress simulation results and measurements[19] of inside (a) and outside (b) surfaces
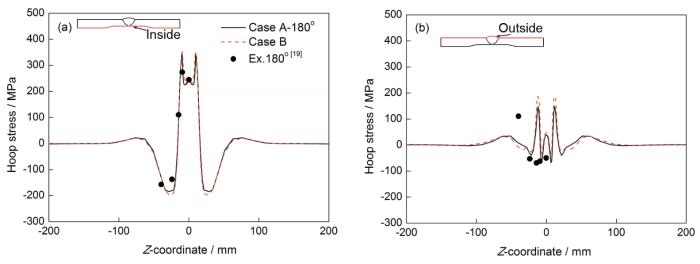
图7为Case A 180°截面和Case B内表面与外表面的周向残余应力分布及对应的实验结果[19]。总体而言,2D轴对称模型和3D模型计算得到的结果与实验结果吻合较好。但是在图7b中,实验结果与计算结果存在一定的偏差。焊后为了贴应变片进行的机械打磨和焊前机械加工带来的初始残余应力是导致偏差出现的原因。此外,外表面近缝区的周向应力幅值随轴向距离变化很敏感,这也影响了残余应力的测量精度。
图7 内表面和外表面周向残余应力模拟结果与测量值[19]对比
Fig.7 Comparisons of hoop residual stress simulation results and measurements[19] of inside (a) and outside (b) surfaces
通过上述详细比较和分析可知,2D轴对称模型与3D模型模拟的残余应力结果差异很小,而且与测量结果吻合较好,这也验证了2D轴对称模型在计算小尺寸圆管对接接头焊接残余应力时,具有较高的精度。对于小尺寸的圆管,在不考虑始终端应力分布[17]时,可以用2D轴对称模型代替3D模型计算环焊缝稳定区残余应力,进而大幅节省计算时间。在本研究中,Case A的计算时间为289 min,而Case B的计算时间仅为0.75 min。
为了比较不同尺寸模型的残余应力计算结果,本工作选取了3D模型180°截面上的横向与纵向残余应力分布与对应的2D轴对称模型计算结果进行比较(图8)。可以看到,所有案例的焊缝及近焊缝区均呈现较高的拉应力,局部区域的应力峰值远高于母材的常温屈服强度(220 MPa),这是由于焊接时沿焊缝方向(周向)的拘束较大导致的。另外,在力学模型中,采用各向同性硬化准则考虑了材料的加工硬化效应,因而纵向残余应力的峰值会远高于材料的屈服极限。在图8中,随着模型尺寸(壁厚和内径)的增加,最大拉应力出现的位置从圆管内表面逐渐过渡到靠近外表面的区域,而最大压应力始终出现在焊缝两侧靠近内表面的区域。对于小尺寸圆管模型(Case A与Case B)而言,2D轴对称模型与3D模型计算的峰值拉应力相对偏差仅为1.9%;对中尺寸圆管模型(Case C与Case D)而言,两者之间的偏差为2.1%;而对大尺寸圆管模型(Case E与Case F)而言,它们的相对偏差更大一些,但是也没有超过6.0%。总体上来看,2种计算方法得到的周向残余应力分布非常相似,且峰值应力的差别也较小。
图8 3D模型180°截面和2D轴对称模型的周向残余应力分布对比
Fig.8 Comparison of hoop residual stress distribution in 3D model 180° section and 2D axisymmetric model
Color online
图9为Case A~F的轴向残余应力分布云图。根据Dong[27]的研究,环焊缝在厚度方向上轴向残余应力可以分为弯曲型(bending-type)和自平衡型(self-equilibrating-type) 2种类型。在本研究中,小尺寸圆管(Case A与Case B)的轴向残余应力沿厚度方向的分布符合弯曲类型,即沿厚度呈现拉应力-压应力的分布形式,且外表面为压应力,内表面为拉应力。中尺寸圆管(Case C与Case D)和大尺寸圆管(Case E与Case F)为自平衡类型,即在厚度方向上呈现拉应力-压应力-拉应力的分布形式。比较Case E与Case F可知,靠近外表面的应力分布基本吻合,但是靠近内表面的焊缝及近焊缝区域,2种模型计算的轴向残余应力值存在较大偏差,这是由于焊接时轴向拘束较小,轴向应力对拘束变化更为敏感,而2D轴对称模型不能很好地反映焊接熔池在移动过程中的局部拘束。而且随着模型尺寸和焊道数目的增加,一方面2D轴对称模型与3D模型在焊接熔池附近局部拘束度的差异变大,另一方面,靠近圆管内壁的区域在经历多次热循环后,2种模型计算轴向残余应力的偏差会逐渐积累。对于大尺寸圆管模型,靠近圆管内壁1/5厚度的区域,3D模型计算的峰值压应力为-279 MPa,而2D轴对称模型计算的应力峰值仅为-121 MPa,显然2种模型在该区域计算的轴向残余应力值存在较大偏差。
图9 3D模型180°截面和2D轴对称模型的轴向残余应力分布对比
Fig.9 Comparison of axial residual stress distribution in 3D model 180° section and 2D axisymmetric model
Color online
图10a为焊缝中心线上(沿厚度方向)的周向残余应力分布,可以看到Case A与Case B,Case C与Case D计算结果基本一致,而Case E与Case F靠近内表面的区域,2D轴对称模型计算的压应力区域略窄一些。总体上来看,2D轴对称模型与3D模型计算的周向残余应力吻合较好。图10b为焊缝中心线上的轴向残余应力分布。比较Case E与Case F可以看到,在靠近内表面的区域,轴向应力呈压应力,但是2D轴对称模型计算的轴向应力峰值明显偏小。可见,轴向应力对拘束变化更敏感,用2D轴对称模型计算的轴向应力偏差较大。
图10 周向和轴向残余应力沿焊缝中心线的分布对比
Fig.10 Hoop (a) and axial (b) residual stress distributions along the weld centerline (x—distance from inside surface)
Color online
(1) 整体上看,2D轴对称模型计算的热循环曲线与3D模型计算结果比较吻合,且尺寸因素对2D轴对称模型计算温度场精度影响较小,验证了2D轴对称模型计算温度场的有效性。
(2) 对于小尺寸圆管,2D轴对称模型与3D模型计算的残余应力结果趋势一致,且与实验测量结果吻合较好,验证了2D轴对称模型计算残余应力的有效性。
(3) 改变模型尺寸时,2D轴对称模型与3D模型计算结果整体吻合较好,但在靠近内表面的焊缝及近焊缝区域,焊接残余应力的幅值和拉压应力区域的大小存在一定差别,且差别随圆管尺寸的增加而增大。
(4) 从提高计算效率以满足工程应用需求角度出发,对于小尺寸圆管,在不考虑始终端应力问题时,可以用2D轴对称模型代替3D模型计算环焊缝稳定区残余应力,从而节省大量计算时间;而对于大尺寸圆管焊件而言,也可以用2D轴对称模型快速地获得多层多道焊残余应力分布,但是要注意靠近圆管内壁1/5厚度的区域附近的应力值有一定精度损失。
图1

1 实验方法
图2
2 数值模拟方法
2.1 有限元模型
图3
Case
Model
d / mm
t / mm
d/t
M
A
3D
114.3
8.6
13.3
42200
B
2D
422
C
3D
348.5
26.2
13.3
139200
D
2D
870
E
3D
665.0
50.0
13.3
226240
F
2D
808
2.2 温度场计算
图4
2.3 应力场计算
3 结果与分析
3.1 温度场计算结果
图5

3.2 应力场计算结果与测量结果对比
图6

图7
3.3 圆管尺寸效应对2D轴对称模型的残余应力计算精度影响
图8
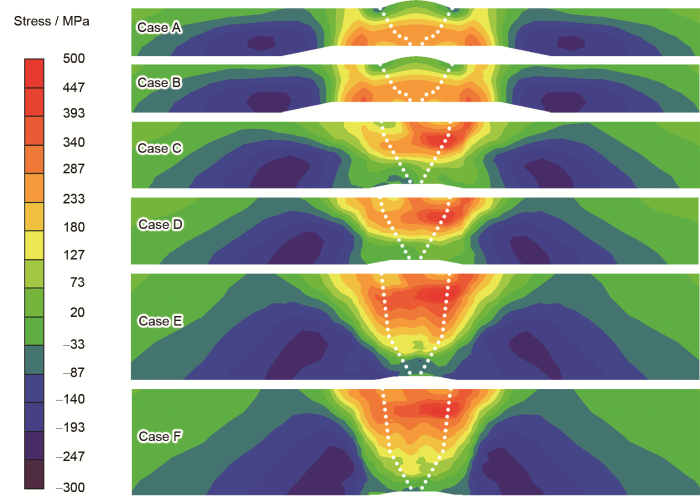
图9
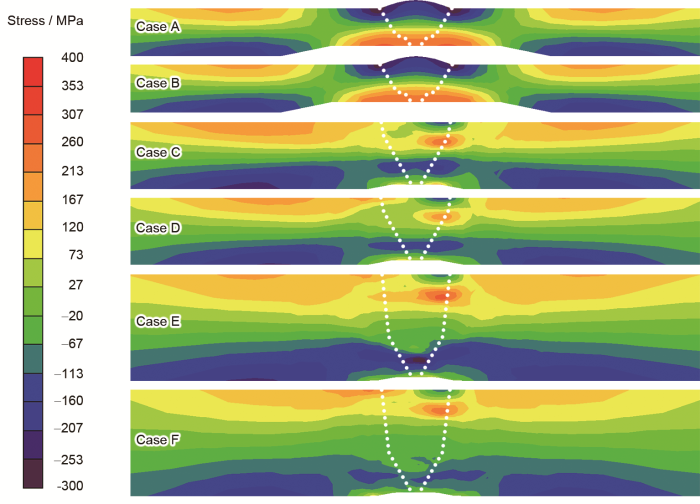
图10

4 结论
来源--金属学报







 沪公网安备31011202020290号
沪公网安备31011202020290号
