分享:装甲防护陶瓷-金属叠层复合材料界面研究进展
1.
2.
将陶瓷与金属以一定顺序逐层叠加,可制成叠层结构的复合材料,兼具陶瓷高强度、高硬度、低密度及金属强延展性的特点,从而应用于防弹装甲材料。但叠层材料存在界面结合弱、受冲击时裂纹易在界面处产生,且裂纹尖端应力集中导致界面处材料易脱黏等问题。本文针对陶瓷-金属叠层复合材料的界面结构及结合强度的问题,从界面结构的制备和观察、界面断裂的相场模拟、界面抗冲击性的有限元模拟和界面强度的第一原理计算等方面进行了综述,并对未来发展方向提出建议。
关键词:
现代战场瞬息万变,要求军队能更快速移动和反应,因此装甲在满足保护人员装备安全基础上必须轻量化。为满足装甲防御性能及机动性能要求,现代装甲材料要求“高强度、高硬度、高韧性、低密度”,简称“三高一低”[1,2]。
受自然界中贝壳片层复合结构增韧机理启发[3,4],研究人员进行了仿生学设计,把不同材料按一定顺序叠放、成型,制成叠层材料,其中陶瓷-金属叠层复合材料是最广泛应用于战场车辆装备的装甲结构[5]。
陶瓷材料强度高、硬度高、密度低和抗冲击性能好,在汽车、电子设备、军事、航天等领域应用广泛,但其延展性差、脆性严重的问题制约着其进一步发展;金属材料虽然抵抗弹性形变能力不如陶瓷,但抗拉强度、屈服强度高,尤其高延展性可弥补陶瓷韧性差的缺点。表1[6]和表2[7~9]分别列出了一些常见陶瓷和金属的力学性能。将金属与陶瓷以特定结构结合就可获得兼具高强度、高刚度又具有高韧性的陶瓷-金属叠层复合材料[5,6]。
表1 几种常见陶瓷的性能[6]
Table 1
Table 2
装甲防护的基本原理是消耗弹丸能量,使弹丸减速并达到无害。装甲结构主要以高强度、高硬度陶瓷材料(如:B4C、Al2O3等)作为面板,通过微破碎过程吸收能量;高延展性金属材料(如:Ti、Al等)作为背板,通过塑性变形来吸收能量[10]。
陶瓷材料抗侵彻原理为:(1) 当弹丸击中陶瓷表面时弹头会变钝,冲击点附近的陶瓷会由于其低韧性而大量破碎形成许多碎块,着弹点下方呈现一个破碎区域,弹丸在接触大量陶瓷碎块过程中耗散大部分动能,使陶瓷面板起到抗弹作用[11,12];(2) 由于陶瓷本身高硬度的特点,变钝的弹丸在高速冲击陶瓷面板时自身也会破碎成许多块,分散的弹丸碎块整体动能大幅下降,达到抗弹效果[13,14]。由于陶瓷本身的脆性,其受到弹丸冲击时发生断裂而不是塑性变形,所以在拉伸载荷作用下,断裂往往发生在非均质处(如孔隙和晶界上)。使应力集中降低可以有效提高陶瓷装甲材料防护性能,装甲陶瓷应当是孔隙率低和细晶粒结构的高质量陶瓷。陶瓷吸收能量的能力与陶瓷的硬度、弹性模量有关,可以用弹道质量因子(M)来衡量陶瓷的抗弹性能:
式中,E为弹性模量,H为硬度,ρ为密度。可以看出,陶瓷的弹性模量和硬度越大,密度越小,抗弹性能越高,陶瓷对于动能的吸收能力越强。
破碎的弹丸和陶瓷碎块会继续冲击,对人员和设备造成伤害,所以需要高延展性的金属作为背板,通过塑性变形来吸收残余动能,防止碎块造成二次伤害[15,16]。
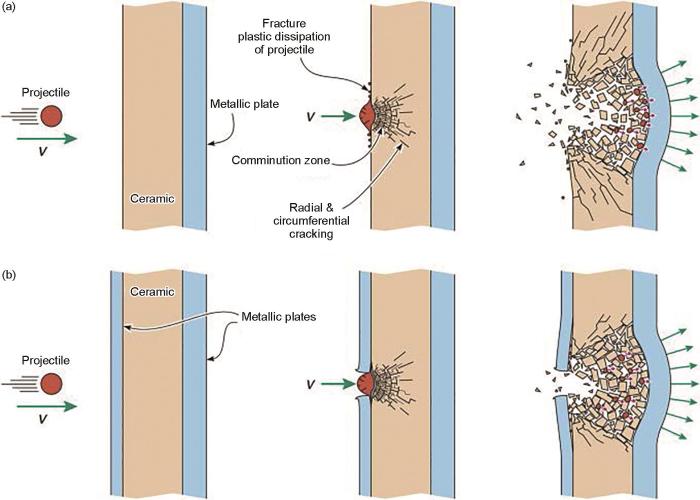
图1a[16]展示了陶瓷-金属叠层装甲抗侵彻机理。弹丸以高速V冲击陶瓷面板,弹丸与着弹点周围陶瓷同时破碎,大面积破碎区域将弹丸动能传递到比原来冲击区更大面积的金属背板上,有利于背板吸收大部分能量[17]。破碎的弹丸碎片向四周飞散,使剩余动能耗散[18,19]。但四处飞散的碎片也容易使周围其他人员、设备受到损伤。图1b [16]所示是金属-陶瓷-金属叠层装甲抗弹机理示意图。陶瓷层外部包覆一层金属,弹丸和陶瓷碎片不易四处飞散,可有效避免二次伤害[20]。此外,外部金属面板包覆使中间陶瓷层在击碎的同时易膨胀,可增大碎片相对吸收能量面积,且金属面板参与吸收动能,使整体吸收弹丸动能的能力得以提高[21]。
图1 由金属板支撑的陶瓷和装在金属或聚合物外壳中的陶瓷弹丸撞击的变形/破坏顺序的示意图[16]
(a) a ceramic tile backed by a metallic plate
(b) a ceramic tile encased within a metallic or polymer case
Fig.1 Sketches of the deformation/failure sequence for a projectile impacting (V—velocity)[16]
当前陶瓷-金属叠层复合材料常用结构是陶瓷面板-金属背板型[22],但陶瓷面板和金属背板的波阻抗失配严重[23,24],界面匹配度低,当材料内部应力增大时,可能导致陶瓷板承受外力冲击而快速崩裂[25,26]。在陶瓷面板与金属背板之间采用环氧树脂或聚氨酯作为黏结层,可改善界面强度,使陶瓷板在吸收冲击能量方面有极大提升[27,28]。但由于黏结层与陶瓷、金属的力学性能差异很大,陶瓷和黏结层之间力学性能不连续,尤其是界面弹性模量由陶瓷面板的300~500 GPa骤降到金属背板不足100 GPa,会导致界面应力不连续而引起应力集中。所以采用黏结层的方法无法彻底改善陶瓷与金属界面的结合问题[29,30]。
要从根本上改善陶瓷-金属叠层复合材料的界面结合问题,需要从改善陶瓷板韧性及提高金属强度入手,通过改变面板和背板成分提高叠层材料整体性,使材料接触界面不发生性能骤变,如通过陶瓷增韧及加入石墨烯等纳米增强相提高金属背板强度[31];或者从如何协调陶瓷面板与金属背板之间的协同关系,增强层间结合强度入手,通过加入涂层在材料界面生成新相来提高界面结合或者对叠层结构进行改进等[32,33]。
无论采用哪种结构方式,陶瓷-金属界面结合状况直接影响复合材料的力学和物理性能,陶瓷-金属界面的结合强度不仅决定金属与陶瓷之间载荷的有效传递,而且是建立复合材料界面结构-界面结合性能-宏观力学性能之间关系的桥梁,也是复合材料跨尺度模拟必不可少的初始参量,更是发挥复合材料功能特性的关键[34,35]。
选择与优化界面结构时,层状材料界面是否发生反应、界面结合力强弱和界面结构对整体材料的影响是需要关注的重点[36],可通过实验、相场模拟、有限元数值仿真及第一原理计算等方法对叠层材料界面进行研究分析和改进。
增强相富集区分层分布可降低裂纹尖端的应力因子和三向应力集中水平,并通过隧道裂纹、裂纹偏转和压缩应力增韧等方式,大大提高材料韧性和抗冲击性。图2[37]是Ti/Al2O3叠层复合材料的横截面及裂纹扩展示意图。可以看出,Ti与Al2O3陶瓷层界面区过渡晶粒的出现使各层界面的结合更加紧密,过渡区使裂纹扩展方式由单一扩展向混合扩展模式转变,从而使叠层材料力学性能优于均质材料。
图2 Ti/Al2O3叠层复合材料组织演变及裂纹扩展路径示意图[37]
Fig.2 Schematic illustration of the microstructure evolution and crack propagation path of laminated Ti/Al2O3 composite[37]
李雨蔚等[38]以SiC粉作为增强层的增强相,Cu粉为黏结相,Cu箔作为延性层,首先采用浸涂方法在Cu箔上制备SiCp/Cu涂层,制备出SiCp/Cu-Cu箔叠层试样。图3a和b[38]分别为SiCp体积分数为20%与30%的复合材料拉伸断口的SEM像。从图3a[38]可以看出,含20%SiCp的SiCp/Cu-Cu箔复合材料的致密度较高,SiCp与Cu箔的界面结合非常好。在图3b[38]中,当添加SiCp体积分数达到30%后,复合材料中出现大量团聚颗粒和气孔,断口表面比前者粗糙和疏松,增强层处断裂方式主要为沿晶断裂,表现出明显的脆性断裂特征,这主要由于一方面SiCp发生团聚,使材料中存在大量气孔;另一方面SiCp和Cu颗粒界面结合很差,裂纹很容易沿颗粒界面扩展导致复合材料力学性能较差。图3c和d[38]分别为不同SiCp体积分数的SiCp/Cu-Cu箔复合材料横截面形貌的SEM像。可以看出,叠层试样层之间的界面结合非常稳定,没有发生反应产生其他杂质,界面结合主要依靠Cu箔与SiCp的机械咬合以及Cu粉做为黏结相在Cu箔之间的融合扩散实现。当SiCp体积分数达到30%时,材料发生开裂,且开裂处发生在层内部而非层界面处,这是由于随着SiCp体积分数的增加,Cu颗粒被分割开来,加热熔融时能够互相接触并长大的Cu颗粒数目减少,大片团聚在一起的SiCp导致此处产生空隙,烧结完成后产生裂纹使材料开裂。力学测试结果表明,当SiCp的体积分数为20%时,材料的抗拉强度与屈服强度都达到最大值,分别为226.5和113.1 MPa,比纯Cu箔叠层材料分别提高了28.9%和175.6%。
图3 不同SiCp体积分数的(SiCp/Cu)-Cu箔复合材料断口以及横截面形貌的SEM像[38]
(a) 20%SiCp (b) 30%SiCp (c) 15%SiCp (d) 30%SiCp
Fig.3 SEM images of fracture surfaces (a, b) and cross section (c, d) of (SiCp/Cu)-copper foil composites with different SiC volume fractions[38]
金旗等[39]采用箔-纤维-箔的叠层方式,将Ti箔、SiC纤维、Ti2AlNb箔按照顺序叠放,纤维外层还有2 μm厚的碳涂层,采用真空热压技术制备出叠层材料样品。通过分析SiC纤维与Ti的界面行为发现,SiC/Ti界面由反应产物TiC和未反应碳涂层组成,其中TiC厚度约为0.8 μm,未反应碳涂层厚度约为1.3 μm,表明碳涂层通过消耗自身以避免SiC纤维的损伤,未反应碳涂层可起到协调纤维与基体变形的作用,实现载荷有效传递。因此,添加SiC纤维后,相比不加SiC纤维前,密度达到4.3291 g/cm3,下降了3%;高温抗拉强度达526.62 MPa,增加了22%;弯曲强度达1506 MPa,提高了19%;冲击韧性提高了15%;断裂韧性提高了3倍,为43.35 MPa·m1/2 。
Han等[40]采用真空热压烧结和热等静压工艺制备了连续的Al2O3陶瓷纤维增强Ti/Al3Ti金属间化合物叠层复合材料。对Ti与Al3Ti界面进行能谱(EDS)分析,发现经过热等静压后的复合材料Ti、Al、V等活性元素在Ti与Al3Ti界面层中的含量均存在波动。Ti和V原子从Ti层扩散到Al3Ti金属间化合物层,而Al原子沿相反方向扩散。但Al并没有完全扩散到界面反应区,在Ti和Al3Ti之间的界面上观察到Al2Ti亮灰色均匀致密区域,表明界面处具有很好的结合。
简单地将陶瓷和金属堆叠形成叠层结构的复合材料其增强效果有限[41,42],陶瓷-金属界面的润湿性对其增强效果具有重要影响[43,44]。在金属-陶瓷层状复合材料制备过程中,界面结合受界面润湿性、界面缺陷和界面反应等多方面因素影响,其中润湿性是影响金属-陶瓷层状复合材料综合性能的关键因素之一。著名的Young-Dupre方程是研究金属-陶瓷界面润湿性的理论基础[45]。
当固体、液体和气体三相接触时,由于界面处分子的固有引力,界面能将以界面张力形式出现在任何两相之间,在固、液、气三相接触后,系统Gibbs自由能函数趋于下降。在表面张力作用下,固-液界面取代固-气界面的过程称为润湿[46]。根据润湿程度可大致分为3类:润湿(吸附润湿)、浸泡(浸入润湿)和铺展润湿[47]。在陶瓷-金属连接的复合材料中,除上述润湿类型外,还存在反应性润湿。反应性润湿的本质是当金属熔化时,它将吸附在陶瓷表面,然后元素扩散并溶解陶瓷基体。同时,随着化学反应的发生,润湿实现了金属在陶瓷表面的扩散[48,49]。通常用于改善陶瓷-金属界面润湿性的方法是:合金化、表面涂层技术、提高润湿温度和使用保护性气氛等。
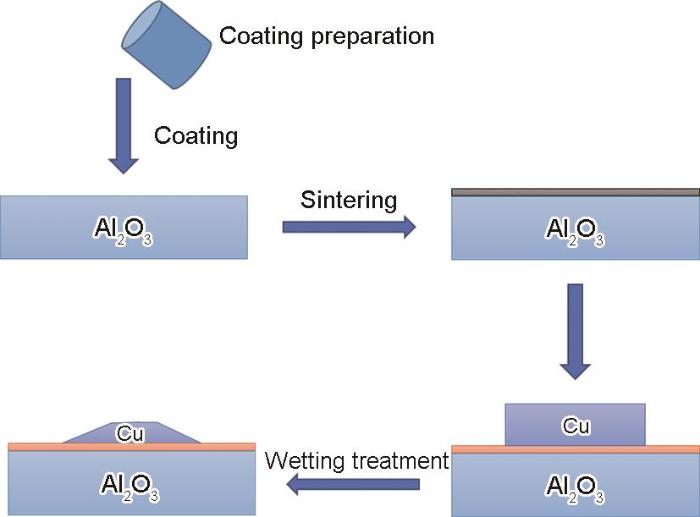
赵敬忠等[50]制备了三维网络SiC结构增强铝基复合材料,向铝基金属中添加了Mg和Si等元素,合金元素的添加破坏了Al2O3膜并削弱了其抗渗透性,加快了无压渗透过程。刘兰霄[51]研究了真空和Ar + 3%H2条件下镍合金和Al2O3陶瓷的润湿性,发现熔融金属Ni/Al2O3在真空下界面反应更强烈,界面润湿性更好。王文祥[52]采用表面涂层技术(如图4[52]所示)来改善Al2O3/Cu叠层复合材料的界面结合问题,首先制备CuO/CuO-Ni涂料并在Al2O3陶瓷基板涂覆涂层,在富氧条件下进行烧结预处理,使Al2O3层与涂层发生反应形成过渡层,随后用200 μm厚的Cu箔做中间层,通过润湿工艺连接经过涂层改性的陶瓷基板,另一侧陶瓷基板也采取同样工艺,最终得到Al2O3/Cu/Al2O3叠层复合材料。对Al2O3/Cu界面进行X射线衍射(XRD)分析,结合界面微观形貌得出,涂层在1100℃下可能沿着Al2O3晶界发生长距离的溶解互扩散迁移,同时与Al2O3发生反应生成新相,原有涂层转变为CuAl2O4、CuAlO2以及夹杂Al2O3的复合层,界面结合很差且过渡层有许多孔缺陷,随着润湿温度提高,过渡层产物逐渐完全变成连续致密的CuAlO2,反应过渡层的生成能够改善润湿性,实现熔融Cu在Al2O3陶瓷表面的润湿铺展,且生成的过渡层与Al2O3和Cu界面结合良好,叠层材料整体非常稳定,对复合材料进行抗弯强度测试,发现抗弯强度可达410 MPa。
图4 表面涂层技术工艺图[52]
Fig.4 Process drawing of surface coating technology[52]
国内外对陶瓷-金属叠层材料的界面研究主要集中于界面处的结合机理及界面反应产物对界面结合的影响。叠层材料界面通常由界面两侧材料成分相互扩散及材料的机械咬合和制备过程中材料在异质界面发生反应生成金属化合物等新相来提高叠层材料整体性[53,54]。虽然金属-陶瓷层状复合材料可以弥补陶瓷本身断裂韧度不足的缺点,但过高的界面强度会使增强体材料和基体之间的应力无法缓解而引起应力集中,使复合材料的强度和断裂韧性降低;界面强度太低也会导致增强体在加载过程中从与基体之间的界面脱落,从而导致复合材料强度下降。因此,有必要控制界面处裂纹等缺陷的产生,提高界面结合强度[55]。
外力冲击下,叠层材料界面是发生断裂的薄弱环节,对这种复合材料进行完整的失效分析,发现裂纹可在具有先验未知裂纹路径的基体内传播,也可沿着2种不同材料之间的界面传播。一系列材料失效问题一般都由裂纹的产生、扩展、传播及分叉等引起,研究界面裂纹成为研究叠层材料界面强度问题的关键[56,57]。
裂纹扩展在叠层复合材料中大致有3种情况,即裂纹偏转、多重裂纹扩展以及裂纹桥接。当发生裂纹偏转时,裂纹平面将会在垂直于张应力方向上重新选择取向,这就造成裂纹扩展路径的增加[58]。裂纹的偏转可以促使其远离平面应力的最大位置,且发生偏转的裂纹越长,裂纹偏转的角度越大,则越能够有效地降低裂纹的尖端局部应力。当裂纹在金属和陶瓷界面发生偏转后,裂纹尖端的向前驱动力大大降低,裂纹穿过下一层金属就需要更多的时间并消耗更多的能量,因此,裂纹偏转有利于材料韧性的提高。多重裂纹扩展是由温度变化引起的热膨胀差或由相变引起的体积差导致的,会在分散增强相和陶瓷基体相之间产生均匀分布的裂纹[59]。在主裂纹扩展时,这些均匀分布的微裂纹将促进主裂纹分叉,增加扩展过程中的表面能,从而阻碍了裂纹的快速扩展[60],这是传统叠层复合材料的增韧机制。裂纹桥接是指通过增强体连接扩展裂纹2个表面而形成裂纹闭合力,从而使脆性基体材料增韧的方法。
目前研究裂纹动力学的数值模拟方法主要有[56]:单元失效法、界面单元法、扩展有限元法和相场法等,其中相场法通过描述序参量在弥散边界的演化而获取裂纹的动态路径和位置,从而避免显式追踪裂纹面,可以处理复杂的多裂纹相互作用问题,同时相场模型容易耦合外场、网格收敛性好,因此在研究复杂裂纹动力学方面具有优势。相场法历经30多年的发展,已成为模拟材料微结构热力学及动力学的有力手段,广泛应用于研究材料的凝固[61,62]、固态相变[63,64]等动力学过程。
基于Griffith能量理论[65],Francfort和Marigo[66]提出了断裂变分模型,使模型可以处理复杂构型,Bourdin和Francfort[67]引入相场序参量描述弥散断裂面。此后,采用相场法研究材料界面裂纹动力学问题快速发展。目前断裂相场模型主要集中于脆性断裂[68~70],超高速或高速冲击过程的材料失效通常是由于脆性断裂,脆性断裂相场在多场问题中自由能密度函数
式中,
高速冲击过程伴随高温,因此也会涉及延性断裂,目前延性断裂相场模型相对匮乏。Duda等[71]给出了一种考虑塑性变形的脆性断裂相场模型,令插值函数只作用于弹性能(未对弹性能进行拉压分解),表明弹性能是裂纹扩展的驱动力,而塑性能作为耗散项不驱动裂纹扩展,该模型并不能有效描述延性断裂。其后,Ambati等[72]基于Duda模型,在插值函数中引入“等效塑性变形参数”来考虑塑性应变的累积和局部效应,从而实现了延性断裂的相场模拟。另一种思路则是从“断裂能级”的角度出发,认为延性断裂和脆性断裂所耗散的表面能具有较大差异,通过延性断裂和脆性断裂不同的Gc来实现2者相互转变的延脆耦合模型。
Liu等[73]在研究异质材料微观界面脆性断裂时,耦合运用了脆性断裂相场模型、局部线性嵌入(locally linear embedding,LLE)流形学习方法和非线性降维方法,对纤维增强复合材料中的增强纤维与基体间裂纹扩展以及基体裂纹的产生和扩展进行了模拟和分析;采用LLE构建了数据流形,对有限元计算的等效体积单元(representative volume element,RVE)模型中的所有微裂纹路径提取微观采样点,以最少计算量精确地重构与任何其他微裂纹模式相对应的输出数据,即固定负载下的相场模拟的裂纹演化。对比了提取100、200、300、400、464和496个微观结构的结果,显示当提取496个采样微观结构时可以成功模拟出不同类型微裂纹扩展路径。流形学习方法在固定载荷的复合材料中输入是初始裂纹路径(即相场的初始条件),输出是裂纹演化过程及平衡状态;同时发现,LLE特别适用于具有大量相似的高维数据的问题。
Russ等[74]采用断裂相场模型,研究了3D打印聚合物基复合材料在大变形下的破坏行为,并与实验结果进行了比较。Li等[75]基于相场法提出了弹塑性复合材料界面损伤模型,该方法可处理材料微观结构中弹塑性断裂和界面裂纹的产生、传播和相互作用。Dean等[76]提出了一种考虑短纤维增强聚合物基复合材料各向异性的相场模型,在典型应用中该模型显示出稳定性。Hirshikesh等[77]运用相场法研究了单轴拉伸下恒/变刚度复合材料层合板断裂过程,揭示了裂纹扩展路径和纤维-基体界面对裂纹扩展路径的影响。Wu等[78]利用相场法模拟了准静态载荷下炭黑增强复合材料的损伤形核和膨胀过程,并通过实验数据验证了超弹性相场模型。Van Do等[79]基于变分相场模型分析了具有裂纹的功能梯度板的热屈曲行为,讨论了考虑梯度板中性面和中间面之间差异的必要性。Carlsson和Isaksson[80]结合高速相机和动态相场有限元模拟研究了木纤维聚乳酸复合材料和纯聚乳酸的动态断裂过程,发现相场模型很好地预测了能量释放、裂纹扩展速率和裂纹尖端速率与裂纹分支形貌之间的关系,但高估了木纤维复合材料中裂纹分支的数量。可见,相场法已有效应用于复合材料裂纹扩展和叠层结构裂纹扩展路径的研究中。
Khaderi等[81]使用相场模型研究仿生复合材料中裂纹扩展问题,其特征在于无机和有机相的分层排列,根据模量失配程度和有机层厚度展示了不同的裂纹扩展方式。
Paggi和Reinoso[82]通过对复合材料施加载荷,观察了初始裂纹对界面的影响,由于裂纹扩展受材料1与材料2之间弹性不匹配的影响,故引入Dundurs参数α和β来表征双材料体系的弹性失配。
式中,μi、νi (i = 1、2)分别表示2种材料的Lamy常数和Poisson比。结果发现,裂纹扩展有3种不同机制,取决于界面断裂韧度与相应体积之比:(1) 裂纹沿界面扩展,对应于材料2比界面坚硬得多的情况;(2) 裂纹沿一侧偏转;(3) 裂纹贯穿界面后发生偏转。这3种情况的曲线如图5a[82]所示。从该图中选择标记为A、B和C的3种材料结构分别对应上述3种情况。图5b~d[82]中显示了这3种情况下预测的破坏时垂直位移场的相应轮廓图,通过颜色从蓝色突变为红色来突出界面处的裂纹模式和位移不连续性。分析这些结果可看出,数值预测与基于线弹性断裂力学的理论结果非常吻合。
图5 无量纲垂直位移场的曲线图及对应于图5a中标记为A、B和C的3种不同情况[82]
(b) extend along both sides of the interface
(c) deflection along one side of the interface
(d) penetrate the interface
Fig.5 Graph of the dimensionless vertical displacement field (α—Dundurs parameter) (a) and corresponding three different situations marked A, B, and C in Fig.5a (b-d)[82]
在子弹冲击叠层材料产生裂纹时,裂纹延伸路径为上述3种情况:A材料结构防护效果最佳,但裂纹沿界面延伸后会造成外层脱落,无法连续承受多发子弹冲击;B结构沿裂纹延伸一段后单侧偏转进入背板,材料还可以继续防护;C结构裂纹贯穿界面进入背板,说明材料已经无法起到防护作用。
Zhang和Suo[83]研究了分裂奇点对裂纹在双材料界面延伸或脱黏情况的影响。对于以一定角度撞击双材料界面的裂纹,奇异应力场是2个模态的线性叠加,通常是指数不等的一对共轭复数或2个不相等的实数λ1和λ2。在后一种情况下,更强和较弱的奇点共存被称为分裂奇点。如图6[83]是2种材料界面处裂纹在受到某种角度撞击后裂纹偏转情况。裂纹的边缘位于界面上,与极坐标(r, θ, z)的z轴重合。受到冲击后主裂纹撞击界面有2种情况:裂纹可能会穿过界面在材料另一侧继续扩展或者沿界面扩展发生脱黏现象。通过设定裂纹角度ω为45°和90°对裂纹尖端的奇异应力场在(α, β)的平面上进行等值线划分。并设定了一个无量纲参数来表征断裂过程中的长度尺度上2种模式的比例。最终表明,较弱的奇点依然可以影响界面受到冲击后裂纹贯穿界面或者界面脱黏。
图6 材料2中的主裂纹撞击界面后,裂纹可能继续穿透材料1或剥离界面[83]
Fig.6 After the main crack in material #2 hits the interface (a), the crack may continue to penetrate the material #1 (b), or peel off the interface (c) [83] (The length of the small crack a can represent the size of the defect on the material #1 and the interface, r is the distance that the crack extends through the interface into material #1, ω is the angle of the crack, θ is the angle at which the crack extends to the deflection of the material interface and ? is the penetration angle at which the crack deflection occurs when it hits the interface, σθθis the stress in the θ direction in polar coordinates (r, θ), σrθis the stress in the r direction in polar coordinates (r, θ), σrris the stress between the r axis and the θ axis in polar coordinates (r, θ))
对于超高速冲击实验,一般会通过子弹冲击实验和分离式Hopkinson杆(split Hopkinson pressure bar,SHPB)实验,来分析其在高应变速率下的真实应力变化情况,以及物相组分及微观形貌变化。由于弹丸冲击速率非常高,为了捕捉到弹丸冲击叠层材料的瞬间,通常采取高速摄像机或闪光X射线系统对撞击过程拍照[84,85]。在冲击过程完成之后,对样品迎弹面和背弹面的形貌及组织演变进行观察。SHPB实验是建立在应力波传播基础上,主要测量材料的动态应力应变关系,可用于实测材料在高应变率(100~1000 s-1)下的应力-应变曲线,实现材料变形过程中的恒应变率加载,但对于微秒级超高速冲击实验,仍力有不逮。
因此,将实验研究与计算模拟仿真研究相结合,有助于设计具有更加优越的抗冲击性能的装甲材料。超高速冲击时固体材料会表现出流体性质,涉及高应变率、大变形及流动界面等问题,有限元法能够模拟叠层复合材料的力学性能,从而较准确地求解危险结构部位的应力应变水平[86]。1990年,Yamamoto等[87]基于Hertz接触定律,通过接触力把结构的运动和冲击物联系起来,对小球与Timoshenko梁的撞击问题使用间接模态叠加法(indirect mode superposition method,IMSM)进行了模拟分析。Liu等[88]对具有高体积分数的叠层复合金属的力学行为进行了有限元求解,做出不同层厚的Ti片及固定体积分数的TiBr/Ti复合材料的应力-应变曲线。发现随着Ti片厚度下降,其应变所需的应力也下降。Maiti和Sinha[89]探究了叠层材料层厚度差对材料的影响。Singh等[90]提出用高阶剪切变形理论求解叠层材料的结构特征和力学性能,其侧重于考虑材料特性对固有特性的影响。Messina和Soldatos[91]考虑剪切变形以达到层间应力和位移的连续而提出了二维叠层材料理论。曾东和方岱宁[92]通过无厚度界面元法,对叠层结构陶瓷三点弯曲力学性能进行了测试,对纵向贯穿裂纹采用最大拉应力破坏准则进行模拟,对沿界面扩展的横向裂纹采用无厚度界面元破坏准则进行模拟,研究发现:叠层陶瓷材料的断裂韧性随着层数增加而提高,但增幅也在随之降低,在层数达到20层以后,渐渐开始趋于平缓,断裂韧性提高不再明显。黄勇和汪长安[93]以基体与弱结合界面层相间隔的材料为模型,设定断裂过程中仅产生逐层断裂,主裂纹贯穿层面且与沿着界面横向扩展的微裂纹组成2个部分,将界面弹性应变能的释放率G作为裂纹扩展的判断条件,对叠层结构陶瓷材料断裂过程中的能量和断裂韧性进行计算分析。于英华等[94]通过实验测量弹性模量及Poisson比等数据,基于ANSYS有限元模块对制得的纳米TiC颗粒增强ZA35合金动态结构和性能进行分析,结果显示ZA35/TiC轴套的各阶频率较ZA35均有大幅提升,论证了Hall-Petch 理论的实用性。
Zhang等[44]研究预应力对Al2O3陶瓷面板-Al背板叠层材料抗冲击性能的影响时,认为:预应力可以有效增强陶瓷叠层装甲的抗弹性能,大预应力(274 MPa)弹道极限甚至比无预应力高出25%,之后采用LS-DYNA软件进行有限元数值模拟对实验结论进行验证。在材料模拟制备阶段,首先使用三维建模技术。采用基于Lagrange算法的SOLID164网格划分法来对无预应力、小预应力和大预应力3种样品建模。其中预加应力依靠设定陶瓷盘的初始直径大于钢套筒内径来施加刚性约束实现。在模拟弹丸侵彻装甲的过程中,可以清晰直观地观察和分析弹丸侵彻装甲的各个阶段,如图7[44]所示。子弹冲击的第2阶段:对于预应力样品,由于陶瓷相对完整且坚固,可提供更大阻力,因此抑制了裂纹产生和扩展。而且,将损坏限制在较小区域,损坏的陶瓷被周围陶瓷限制了碎片的后续移动,并不断迫使碎片与弹丸摩擦,消耗掉弹丸的动能,起到很好的抗冲击作用。计算发现,在第2阶段结束时,有预应力与无预应力的弹丸速率相差约90 m/s。在第3阶段结束时,目标A和B都被子弹击穿。但是,具有较大预应力(274 MPa)的样品C成功拦截了弹丸。
图7 数值模拟目标A、B和C在500 m/s下受到弹丸撞击的损伤[44]
Fig.7 Numerically simulated evolution of damage in targets A, B, and C subjected to projectile impact at 500 m/s (Vi—pojectile impact velocity)[44]
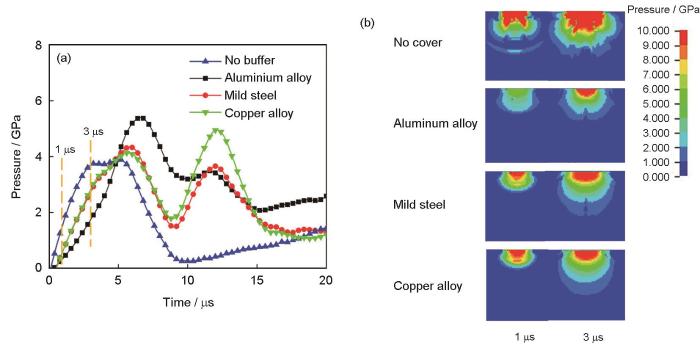
Luo等[95]研究了覆盖板对SiC陶瓷面板-钢背板叠层装甲抗弹性能的影响,采用LS-DYNA软件进行数值模拟分析。为了模拟大规模弹丸侵彻和节省成本,采用Lagrangian法对样品进行三维建模,弹丸和装甲样品是完整的3阶64节点六面体。模拟子弹撞击装甲过程中陶瓷受到的应力曲线以及1~3 μs阶段应力分布如图8[95]所示。从图中可以清晰地观察到:在1~3 μs阶段,采用Al覆盖板的陶瓷样品受到的冲击应力最小。从图8b[95]可以看出,当覆盖板受到弹丸的冲击时,在冲击点中心的弹塑性应力波在覆盖板、陶瓷板和背板之间的界面处反射和传递,且不同材料的弹性阻抗适配度越大,激发的反射波越大,导致弹丸侵彻弹道阻力越大。所以增加覆盖板使得应力波在2个界面间来回传递可以有效消耗动能,增强叠层材料防弹性能。
图8 冲击路径上陶瓷的平均压力与时间的关系和陶瓷沿厚度方向在1和3 μs的压力分布[95]
Fig.8 Average pressure of ceramics under the impact path versus time (a) and ceramic pressure distribution along the thickness direction at 1 and 3 μs (b)[95]
叠层装甲受到弹丸冲击产生大变形,无法简化成小变形线弹性问题,需要利用非线性有限元方法或者无网格方法进行数值求解。采用常规有限元方法分析叠层装甲受到子弹高速冲击问题时,由于每个载荷步都需要重新剖分一次网格,使得计算量迅速增加,计算精度下降,求解困难。而无网格法形函数具有优越的光滑性,能够方便地构造出高阶形函数,并且可以引入能够表明问题特殊性质的函数基底,即选择特定的函数基底分析特定问题,如选择高阶基底分析高梯度问题和选择正弦函数分析具有奇异性的裂纹扩展问题[96]。
无网格数值方法起源于20世纪70年代,通常的有限元分析需要定义节点和单元,而无网格法用点的集合来描述给定部件,不依赖网格,因此在高速冲击等动态大变形问题的非线性计算方面更具有优势,其中最经典的方法是光滑粒子流体动力学(smoothed particle hydrodynamic,SPH)方法,是把连续的物理量用多粒子的集合来插值的数值解析方法。SPH的主要思想是通过一个核函数(kernel function)对离散质点位置的核估计来计算梯度的相关项,这样就不必借用网格求解偏微分的差分,而是将微分形式的守恒方程转化为积分形式,得出在任意一点的各个场变量的核估计[97],用核函数f(x)以积分形式再现物理场函数[98]:
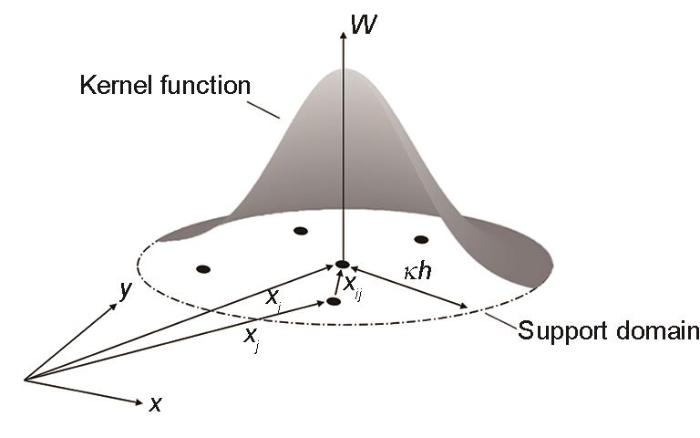
式中,W是核函数,ΔVj是粒子j的体积,xi和xj分别是粒子i和j的位置,xij = xi - xj是粒子i和j之间的相对距离,如图9[98]所示,h是平滑长度,κ是由核函数决定的常数,κh是支撑域(support domain)的半径。体积可以用粒子密度ρj和质量Mj表示为ΔVj = Mj / ρj。
图9 粒子在粒子
Fig.9 Particle distribution and Kernel function W within the support domain of particle i (xi, xj—positions of particles i and j, respectively; xij—relative distance between particles i and j; κh—radius of support domain)[98]
无网格法最初是Lucy[99]提出的解决流体力学方程组时间演化问题的一种Monte Carlo方法。1994年,Belytschko等[100]提出了无网格近似函数,采用移动最小二乘(moving least squares,MLS)近似函数,称作无网格Galekin法。之后,Atluri等[101,102]提出了局部边界积分方程和无网格局部Petrov法,减少了对网格的依赖性。1999年,Wendland[103]将径向基函数引入无网格Galekin法,丰富了无网格的形函数。2002年,Hao等[104]提出了无网格有限元法。2004年,Liu等[105]提出了重构核单元法。无网格SPH法是一种纯Lagrange算法,通过插值性质直接离散化一个给定的连续性方程组,而无需定义空间网格,能够准确模拟物质界面的移动,跟踪物质点的运动轨迹,实现三维空间复杂流场计算;同时计算精度不受物质变形程度的影响,用于处理大型不规则结构、随时间变化的不连续性和大变形以及高应变率问题,无需网格重构,能保证计算精度不受损,因此SPH数值仿真算法非常适用于高速或超高速碰撞等冲击动力学问题。但SPH方法本身也存在一些问题,如拉力不稳定性、粒子不一致、施加位移边界条件困难等[106]。
最优输运无网格方法(optimal transportation meshfree method,OTM)是一种显式增量更新Lagrange无网格计算方法[107],该方法的理论体系由最优输运理论、物质点采样法以及局部最大熵无网格近似结合而成。马天宝等[108]采用OTM模拟铝制弹丸超高速碰撞单层及双层薄靶板问题,通过与实验结果对比,描述了Al在高温高压和高应变率条件下的动态力学响应,验证了OTM模拟超高速碰撞问题的有效性。张天龙等[109]利用OTM模拟了弹丸超高速正撞击单层靶板过程,同时分析了不同量级规模的模型以及不同核心数对CPU并行计算耗费时间的影响。OTM可以有效地克服现有显式分析中能量不守恒的问题;在计算边界处具有Kronecker-delta性质,可以更好地引入位移边界条件;采用物质点与节点结合的方式进行空间离散,由于插值与积分在不同的离散点进行,避免了SPH方法中存在的拉力不稳定性等局限,在未来的高速冲击实验及相应的装甲叠层材料的结构和性能研究中会有更多的应用。
SPH法在大变形等宏观问题上有广泛应用,由于介观系统上限可认为接近宏观尺度,因此介观体系也表现出具有确定性的经典物理学规律,这一尺度上的材料常被称为软物质或复杂流体。然而,该尺度上的数值模拟却陷入一个窘境:如果采用分子动力学模拟,计算成本将非常高昂;如果采用计算流体力学模拟,介观的随机涨落又无法描述。为了解决这个问题,在过去20年里一些介观模拟方法逐渐发展起来,其中耗散粒子动力学(dissipative particle dynamics,DPD)是一种代表性粒子方法[110]。
在超高速冲击陶瓷-金属叠层材料的实验过程中,陶瓷会出现一系列的原子变形、局部熔化和无定型性,包括锥形头、底面滑移和孪晶、菱形孪晶等现象。高速冲击导致的高温条件使得金属材料发生热塑性失稳相变,形成软凝聚态物质,呈现出半流态/流态力学特点,在碰撞影响区发生强烈的相变及微观晶体组织变化[111],与其他软凝聚态物质一样也易偏离平衡态。在大应变变形后,很多材料中都可以观察到狭窄的带状区域,就是由于这种热塑性相变产生流体后冷却形成的。如果在某一特定区域内发生的变形远高于周围区域,代表了一种从均匀变形发展成的非稳态变形,这种变形被称为剪切带[112]。在剪切带形成过程中,变形热效应起了很重要的作用。因此,依据热效应在剪切带形成时所起作用的大小将剪切带分成2类:一种是均热剪切带,在这种剪切带形成过程中变形材料内部的温度分布是均匀的;另一种是绝热剪切带(adiabatic shear band,ASB),这种剪切带的形成强烈依赖于变形时所产生的热效应。由于热效应的作用不同,所以2种剪切带的形成机制也不相同。绝热剪切带一般在材料的动态加载变形过程中出现。形成这种剪切带的原因是在高应变速率条件下,材料的塑性变形功大部分都转变成热,导致了局部温度的急剧升高。温度升高使材料发生了热软化效应,变形进一步集中在此区域,最终形成了一个高温、大变形的窄带区域。最终在周围基体的冷却作用下形成了ASB[113]。
目前,对于高速冲击得到的软凝聚态物质演化过程、形成机理以及ASB内部应力场、温度场等问题的研究均处于第一性原理计算及有限元模拟仿真的理论分析阶段,有待于进一步结合多尺度方法、实验及现场深入探索。
界面结合强度和结合成键方式直接影响复合材料的综合性能。而常规实验往往达不到界面所涉及的微观尺度,第一性原理计算之所以成为界面研究的重要方法,是因为它能够分析界面的原子结构、界面结合强度及界面成键的本质。陶瓷-金属界面的第一原理研究近年来取得了快速发展,不仅可对界面实验进行补充和验证,而且能够在原子和分子尺度模拟界面力学行为,揭示界面结合的本质和界面变形机制[114,115]。
第一性原理计算最早于1990年被应用于金属-氧化物界面计算。Freeman等[116]利用全势线性叠加波函数方法,研究了单层Ag原子与MgO(001)面组成的界面,指出Ag原子在MgO(001)表面的最优吸附位置是在O原子上方。他们还研究了Ag/CdO(001)界面[117]的电子结构、结合能以及单层磁性金属Fe、Pd、Rh、Ru与MgO(001)所组成界面[118,119]的磁性能。
Smith等[120~122]采用自洽局域轨道方法研究Ag/MgO(100)和Al/MgO(100) 2个界面及杂质C和S对界面的影响,发现结合能和界面距离之间满足广义结合能关系,同时指出非自洽的Harris泛函计算与自洽计算结果基本一致。Hong等[123,124]还计算了过渡金属Mo、Nb、V与金属间化合物MoSi2的界面结合以及杂质 C、O、B、S和Nb对这些界面的影响。
以上是早期的金属-陶瓷界面第一性原理计算工作,限于20世纪90年代计算机能力等因素,晶体取向、晶格错配等影响界面的因素并未考虑进去。近年来,第一原理方法不再局限于金属/氧化物界面,已逐渐延伸至金属与碳化物、氮化物等陶瓷界面的计算,并且对影响界面的因素也考虑更加全面。
空位是因原子缺失导致周围电子结构发生变化,是一种常见的晶体缺陷,界面附近空位也会影响金属/陶瓷界面的结合。Zhukovskii等[125]首次使用第一原理方法研究了陶瓷表面空位对Ag/MgO界面的影响,结果显示缺陷界面的结合能比完整界面大一个数量级,说明空位严重影响Ag/MgO界面结合。Matsunaka和Shibutani[126]采用第一原理方法研究了O原子空位对非共格Ni/MgO界面结合的影响,指出空位界面与完整界面的结构非常相似,O空位电荷转移引起Mg2+与金属Ni的诱导离子之间的镜像作用,使空位界面的黏着功大约增加0.1 J/m2 (约15%)。
晶格错配是界面的另一种主要缺陷。Benedek等[127]首次使用第一原理研究了晶格错配对Cu/MgO(222)界面的影响,提出O原子层和Cu原子层由于弛豫作用产生了较大变形,Cu原子在MgO原子上方的结构变形最大,在MgO的3个表面原子上方的结构变形最小。Long等[128]为了平衡界面晶格错配,在金属(Ag, Au, Cu)/Al2O3界面中引入位错网,研究了位错在金属/Al2O3界面引起的变化。
元素在界面的偏析被认为是影响界面结合的重要因素。Liu等[129]使用第一原理方法研究了Mg、Si偏析对Al/TiC界面结合的影响,指出元素偏析对界面的影响程度与元素偏析引起的表面活性及界面应力相关。计算结果显示,Si原子偏析可以稍微改善界面结合,而Mg原子偏析则会减弱界面结合,这与润湿实验的现象相互一致。Dudiy和Lundquist[130]研究了Ti、Al原子在Ag/Ti(C, N)界面的偏聚对结合的影响,结果表明Ti原子偏聚显著增加Ag/Ti(C, N)界面的结合强度,Al原子基本不影响Ag/Ti(C, N)界面的结合。
晶体取向也是影响界面结合的一个重要因素。Dudiy和Lundquist[130]研究了晶体取向对Ag/Ti(C, N)界面结合的影响,3个低指数界面分离功和界面能的顺序是(001) < (011) < (111),Ti(C, N)的表面能、单位界面面积上Ag—Ti和Ag—(C, N)键的数目及Ag—Ti键的强度共同决定界面的性能。Long等[128]计算了Ag/MgO (001)、(110)和(111)界面的黏着功,结果显示Ag/MgO(111)界面的黏着功最大,Ag/MgO(001)界面的最小,同时指出由于Ag/MgO(001)晶面的Ag-Mg和Ag-O原子势对不能直接转移到Ag/MgO(110)和Ag/MgO(111)界面,3个界面原子之间具有不同的结合特征。
Deng等[131]采用第一原理计算了Al(111)面与TiB2(0001)共格界面黏附功和界面能,研究了TiB2对Al/B4C复合材料性能的影响,并计算了界面掺杂Mg、Si原子后的电荷密度与态密度,发现掺杂Mg、Si后会减弱Al/TiB2界面能,从而抑制TiB2形成,增强Al/B4C复合材料力学性能。Rao等[132]研究了Ti(0001)面与TiN(111)面界面上O、H原子单层对界面结构和黏附功的影响,基于3种原子堆积模式(OT-,SL-和TL-位:OT-位代表Ti侧界面的Ti原子直接放置在TiN侧表面N(Ti)原子的顶部,SL-位代表TiN第2层中N(Ti)原子的顶部,TL-位代表TiN第3层中N(Ti)原子的顶部)和2个TiN(111)面终止层,建立了6种Ti(0001)/TiN(111)界面模型。Ti/N界面稳定性大于Ti/Ti界面,Ti/N界面能均小于零,表明它是热力学稳定的。在Ti/N界面中,N原子的TL堆积模型界面能最小(-3.86 J/m2),表明N的TL堆积模型最稳定。Liu等[133]研究了Al/Ti(C, N)(001)界面结合机制,计算结果与实验值相吻合,界面主要是Al3sp与C(N)2s轨道交叠形成的极性共价键连接。另外,他们指出由于共价键方向性、界面应力及结合能相对较弱的原因,断裂优先在界面发生。
Li等[134]研究了化学计量比对金属/α-Al2O3界面结合的影响,并提出一个对化学计量比敏感的分离功Wsep与金属/Al2O3界面结合强度关系的统一模型:
式中,a、b和c是常数,数值与化学计量比相关;
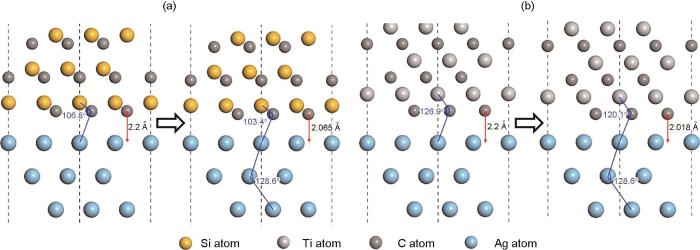
Yang等[135]通过第一性原理研究了Ag(111)/SiC(111)界面和Ag(111)/TiC(111)界面性质,从图10a[135]可以看出,结构弛豫之后,2个界面无明显原子重排现象。结构弛豫之前,界面原子距离和界面处Si—C—Ag键角分别为22 nm和106.8°,结构弛豫之后界面原子距离减小至20.65 nm,且Si—C—Ag键角发生变化分别为103.4°和128.6°。从与Ag(111)/SiC(111)界面相似的图10b[135]中,结构弛豫在Ag(111)/TiC(111)界面上引起原子重排也可以忽略。此外,结构弛豫之后,界面原子距离和界面处Ti—C—Ag键角从22 nm和126.9°减小至20.18 nm和120.1°。表面能计算发现具有C端基结构和TL堆叠顺序的Ag(111)/SiC(111)界面和Ag(111)/TiC(111)界面显示出最高界面稳定性,其中,Ag(111)/SiC(111)界面黏着功Wad和原子间距d0分别为3.78 J/m2和20.65 nm,而Ag(111)/TiC(111)界面Wad和d0分别为4.85 J/m2和20.18 nm。Ag(111)/SiC(111)界面的界面能小于Ag(111)/TiC(111)界面,界面距离越小,界面黏着功越大,界面越稳定。结果进一步表明Ag(111)/TiC(111)的界面结合强度比Ag(111)/SiC(111)界面强。
图10 Ag(111)/SiC(111)界面和Ag(111)/TiC(111)界面在弛豫前后的局部原子结构[135]
Fig.10 Local atomic structures of Ag(111)/SiC(111) interface (a) and Ag(111)/TiC(111) interface (b) before and after relaxation[135]
Liu和Yang[136]采用第一性原理计算,研究了添加Mg的Al(111)/3C-SiC(111)界面结合,发现Si末端和C末端界面在顶部位置分别产生最大Wad,分别为1.86和3.46 J/m2。界面能γint分别为-0.63和-0.24 J/m2。Mg合金化使Si端终结界面Wad从1.86 J/m2增至3.07 J/m2,C端终结界面Wad从3.46 J/m2降低至3.10 J/m2,表明Mg合金化对这2个终端界面产生相反影响。进一步通过电子结构计算表明,这2个终止界面键是共价键、离子键和金属键的混合物。Mg的添加分别提高了Si—Mg键的Si—Al键合状态和C—Mg键的反键合状态的共价键强度,从而使Mg的添加有利于Si末端界面键合,但对C末端界面键合显示出负面影响。
Guo等[137]采用第一原理计算了ZrO2(111)/Ni(111)陶瓷-金属界面的理想机械强度,通过模拟拉伸和剪切变形,优化了具有1层和3层Ni厚度的ZrO2(111)/Ni(111)界面结构,发现对于在[111]方向上的拉伸变形,1层Ni和3层Ni的陶瓷-金属界面模型的Young's模量分别为139.9和60.2 GPa,极限抗拉强度分别为11.6和7.9 GPa。相比之下,1层Ni原子的力学性能要比3层更优。
可见,第一原理方法已成为陶瓷-金属异质界面原子尺度理论计算的有效工具,不仅可以通过建立界面处原子结构,观察成键方式,计算界面能并判断界面稳定性,还可以计算出以特定原子面结合的界面结构的力学性能,对设计叠层材料的成分、工艺具有重要指导作用。
陶瓷-金属叠层材料兼具陶瓷的高硬度和金属的高延展性,抗冲击性能好,尤其适合做为装甲防弹材料,在抗侵彻过程中,陶瓷面板负责减速和破碎弹丸,金属背板通过塑性变形吸收子弹动能,形成完整装甲抗弹体系,但其界面结合存在陶瓷与金属性能差异大、界面结合强度不足、受到冲击材料内部应力增大而容易产生尖端裂纹等不足,陶瓷与金属界面易导致材料性能骤变,裂纹扩展发生偏移而影响性能。受冲击后裂纹最先在层间产生,说明层间结合强度依然不理想,易造成面板与背板脱落。
针对这些问题的研究,主要集中于利用实验研究界面结合及润湿性、利用相场法模拟界面裂纹及断裂、利用有限元仿真研究界面力学结构以及利用第一性原理方法计算界面强度等,都对指导设计最优界面结合叠层材料提供了有益的理论依据。未来研究设计叠层复合材料的主要方向有:
(1) 加强陶瓷增韧研究,使陶瓷面板与金属背板之间匹配度增强,减小陶瓷到金属的性能骤变,使叠层材料性能更加均匀化;加强金属强度研究,在不破坏金属延展性的前提下,可加入纳米强化相制备金属基复合材料以增强金属强度;界面区域应与其两侧基体材料具有高结合强度,形成化学结合或机械咬合,从而减少微叠层复合材料在平行于界面方向受力时分层、开裂等形式失效,降低其各向异性。
(2) 更多引入相场模拟、有限元力学分析及第一原理计算等研究方法,尤其要探索如何将这些方法有机有效地结合起来。相场模拟可对叠层界面受冲击裂纹的产生、延伸路径以及断裂动力学提供可靠的理论依据,有限元力学分析可有效模拟叠层材料在抗冲击损伤演变过程中结构变化机理,第一原理计算可从热力学能量的角度预测和解释界面的稳定性,无网格光滑粒子流体动力学法以及最优输运无网格法能够较准确地模拟材料的破坏全过程而不受材料变形程度的影响,研究不连续不规则大变形时无需重构网格,更适于研究高速冲击导致的材料大变形问题。因此,基于多尺度的实验研究和计算模拟方法的耦合互补是未来设计叠层材料界面的有力工具。
Ceramic
Density / (g·cm-3)
Elastic modulus / GPa
Hardness / (N·mm-2)
Ductile fracture / (MPa·m1/2)
B4C
2.5
400
2900
2.5-2.8
Al2O3
3.6-3.9
340
1800
3.3-4.8
SiC
3.12-3.28
408-451
2500
2.8-3.2
TiB2
4.5
570
2600
3.0-4.0
AlN
2.5-3.2
343
1200
4.0-6.0
Si3N4
3.2
310
1700
4.0-7.0
Metal
Density / (g·cm-3)
Elastic modulus / GPa
Hardness / (N·mm-2)
Ductile fracture / (MPa·m1/2)
Ti
4.506
109
754
80-90
Al
2.7
70
346
20-25
Mg
1.738
13.2
314
50-60
Cu
8.92
110
377
40-60
1 装甲防护陶瓷-金属叠层材料抗侵彻原理
图1
2 陶瓷-金属叠层界面结合及力学性能研究
图2
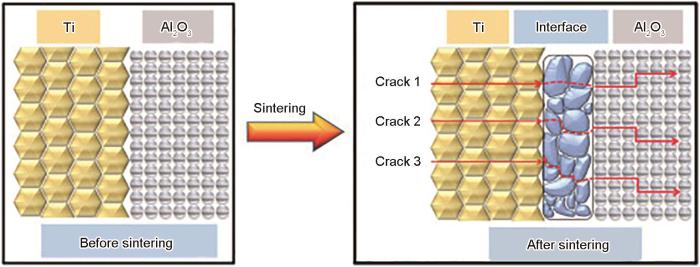
图3

3 陶瓷-金属叠层界面的润湿性研究
图4
4 相场法研究叠层复合材料界面裂纹动力学
图5

图6

5 有限元法研究叠层材料界面结构应力应变
5.1 传统有限元法研究叠层材料界面
图7
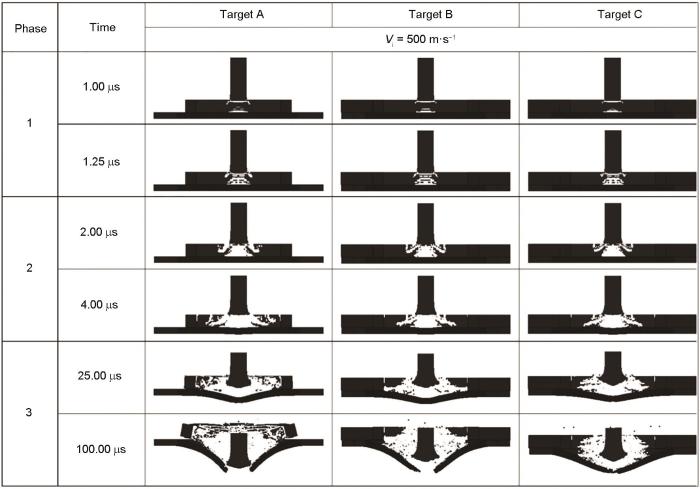
图8
5.2 无网格光滑粒子法研究叠层材料界面大变形
图9
6 第一原理计算研究叠层复合材料界面结合强度
图10
7 结论与展望
来源--金属学报







 沪公网安备31011202020290号
沪公网安备31011202020290号
