分享:Mn和In添加对SmCo7结构稳定性及磁矩影响的第一性原理计算
基于构建适用于第一性原理计算、原子比例准确为Sm∶Co = 1∶7的晶体结构模型,依据实验研究中得到的物相共存结果,对Mn和In掺杂的Sm-Co体系模型进行了系列计算分析。利用热力学计算方法,定量化研究了Mn和In在Sm-Co体系中优先占位特点及掺杂元素占位概率随温度的变化规律。通过Sm-Co合金掺杂体系的能量和电子结构计算,研究了Mn和In单掺杂SmCo7体系的结构稳定性。基于计算结果揭示了Mn和In对掺杂合金体系中原子间相互作用的影响,阐明了提升体系结构稳定性的微观机制,并提出了Mn添加可增加SmCo7合金的总磁矩,揭示了掺杂元素对SmCo7合金饱和磁化强度的影响规律。
关键词:
随着航空航天、电动汽车技术的迅速发展,相关领域对具有高的磁性能且使用温度更高的新型永磁合金提出愈加迫切的要求。已有的商业化永磁合金中,高温磁性能最好的是Sm2Co17型永磁体,但其矫顽力仍然随温度升高而急剧下降,最高使用温度一般小于350℃;而开发先进的高温高性能磁体的目标是把使用温度提高到400~550℃[1~3]。在Sm-Co型永磁材料中,具有TbCu7结构的SmCo7合金的磁晶各向异性场是Sm2Co17合金的1.2~1.4倍,其内禀矫顽力温度系数也较低[4],相对于其他Sm-Co型合金,SmCo7合金具有更突出的高温磁性能的开发潜力。然而,亚稳相SmCo7 (1∶7H)易分解为SmCo5 (1∶5H)和Sm2Co17 (2∶17R)双相组织[5],很大程度上影响SmCo7的高温磁性能,限制其实际应用。因此,深入研究SmCo7亚稳相的稳定性及其转变规律,对于开发高性能SmCo7型永磁材料具有重要的意义。
大量研究者通过实验和计算的方法研究了添加元素对SmCo7相稳定性的影响,目前已有超过20种元素掺杂SmCo7的相关研究报道[6~12]指出,通过添加稳定化元素能够保持SmCo7结构的稳定。掺杂元素基本可以分为3类:一是3d层电子未填满的元素,例如Ti、Zr、Fe、Cu等;二是半导体元素,例如Si和Ge;三是4d层未填满的元素,例如Ag、Mo、Nb等,以及5d层电子未填满的元素,如Hf。不同元素掺杂对SmCo7合金的稳定性具有不同的影响,例如,过渡族元素Zr部分取代Co-Co哑铃对可以使SmCo7具有稳定的TbCu7结构[3];Cr和Mo掺杂SmCo7时优先占据Co的2e晶位,这2种元素掺杂具有提高SmCo7相稳定性的效果[12];半导体元素Si掺杂也可提高SmCo7的稳定性[13];少量Hf掺杂SmCo7时可获得稳定的单相,Hf优先占据Co的2e晶位,当温度升高或掺杂量增加时,Hf开始占据Co的3g晶位,此时会引起SmCo7相失稳转变[14];Al掺杂SmCo7会产生3种相,分别为SmCo7、Sm2Co17和未知相,不能使SmCo7的单相稳定存在[15]。Luo等[16]研究表明,包括Nb和V的15种添加元素中只有Si、Cu、Ti、Zr和Hf元素可以稳定SmCo7单相。而第一性原理计算确定了Zr添加可以使SmCo7的结构稳定,并且得出其占据Co的2e或3g晶位时合金结构最稳定[17]。
掺杂元素在影响SmCo7合金结构稳定性的同时,对磁性能也会产生影响。研究[13]表明,非磁性元素掺杂通常会导致磁矩与饱和磁化强度的降低,例如Si掺杂会削弱SmCo7的磁矩,并且随着Si含量的增加SmCo7的晶胞体积增加,Curie温度和最大磁能积都逐渐降低。Ga或Al取代部分Co时,SmCo7合金的饱和磁化强度和Curie温度明显降低[13,18]。元素取代对Co次晶格的磁矩影响较大[17],添加不同掺杂量的Mo时,SmCo7合金的饱和磁化强度随掺杂元素含量的增加而减小[12]。Cr掺杂体系中,SmCo7-xCrx的矫顽力随着Cr含量的增加显著提高[12]。Cu添加会引起SmCo7合金晶格常数增大,随着合金中Cu含量的增加,Curie温度逐渐降低[19]。
综上所述,采用元素掺杂的方法,可以使SmCo7相稳定存在。尽管已有关于不同种类元素掺杂对SmCo7合金结构稳定性和磁性能影响的大量研究,但是并未获得共识,且所研究的元素种类仍然有限。Liu等[20]通过机器学习的方法预测Mn、Fe、In和Sn等元素的添加有益于维持Sm-Co合金的高饱和磁化强度,在Sm-Co体系磁性材料的成分设计时,掺杂这些元素不明显降低饱和磁化强度,因此可在较大掺杂量条件下追求综合磁性能指标的协同提升。例如,过渡族元素Mn和主族元素In有利于SmCo5体系的综合性能[21],但是关于Mn和In添加到SmCo7合金中对体系稳定性和磁性能影响的研究却鲜见报道。反铁磁元素Mn掺杂可提高SmCo5体系总磁矩,而该元素在SmCo7体系中是否会产生同样效果,值得进一步研究。实验研究[21]得出,In元素掺杂SmCo7会产生SmCo5、Sm2Co17和SmCo7 3种物相,但In原子在混合相中如何影响基体稳定性及其微观机理至今没有明确认识。因此,以上问题需要借助第一性原理计算的方法,从几何构型、电子结构等方面进行深入分析。然而,由于一直缺乏适合第一性原理计算的SmCo7的结构模型,限制了利用第一性原理计算进行相关的研究。
针对以上问题,本工作首先对目前存在的几种用于第一性原理计算的SmCo7的近似模型进行总结分析,并通过深入研究TbCu7结构的特点,建立准确有效的适用于第一性原理计算的SmCo7结构模型。在此基础上,结合前期SmCo5型合金中掺杂元素的筛选结果[20],建立Mn和In 2种元素单独掺杂的SmCo7的模型,基于第一性原理密度泛函理论,计算掺杂体系的总能量、电子结构和磁矩等性质。利用形成能的计算研究掺杂元素对体系稳定性的影响,通过分析电子结构研究掺杂元素对体系稳定性及磁性能的影响规律,由此揭示添加元素对SmCo7结构稳定性和磁性能的作用机制。进一步结合统计热力学分析方法,通过Maxwell-Boltzmann分布概率计算掺杂元素在SmCo7中占位概率随温度的变化,分析温度对体系结构稳定性的影响。
Buschow[4]认为,TbCu7型结构是CaCu5型结构的衍生物,其中Ca位被2/9的Cu-Cu哑铃对随机取代。张昌文[22]建立了SmCo7-xTix的团簇结构Sm5Co28Ti6。Li等[19]建立了含有448个原子的SmCo7无序化的结构模型,但模型中的原子数量过于庞大,不适合第一性原理计算。Chen等[17]建立了含有25个原子的SmCo7.3的近似模型。张哲旭[23]通过实验结果拟合晶格常数的方法建立了SmCo8.5的近似模型,其后华刚[24]在SmCo7超胞的基础上进行简化,得到了SmCo6.75的近似模型。以上几种结构模型中存在的普遍问题是:SmCo7模型是在SmCo5超胞结构中由1个Co-Co哑铃对替代1个Sm原子得到,导致多数模型的哑铃对占比不准确,不能有效地反应SmCo7真实的结构及磁性;而符合SmCo7结构特点的无序计算模型中原子数量却非常大,无法利用第一性原理进行计算。
针对这一矛盾问题,本工作基于Sm-Co基二元合金的晶体结构转变规律分析,建立了Co-Co哑铃对占比准确、单胞中原子数量适合第一性原理计算的SmCo7模型。建立SmCo7结构模型的传统方法一般是在SmCo5单胞基础上按(1 × 1 × 9)扩大9倍后,用2个Co-Co哑铃对随机替换2个Sm原子,得到SmCo7型结构,但问题是Co-Co哑铃对的具体位置以及Co-Co原子间距不能确定,导致无法精确构建SmCo7晶体结构。通过Sm-Co二元合金中相结构转变的研究,发现Sm2Co17 R型结构可由SmCo5转变得到,其转变过程是,SmCo5单胞按(1 × 3 × 3)扩大9倍后,再将得到的9倍SmCo5超胞中的3个Sm原子用3个Co-Co哑铃对进行替代,则完成Sm9Co45到Sm6Co51的转变。如图1a所示,利用Materials Studio 软件建立了Sm2Co17 R相的晶体结构模型。通过对比SmCo7和Sm2Co17中的各位点原子分布情况,发现利用Sm原子逆向替代Co-Co哑铃对,则无需考虑Co-Co哑铃对的Co原子间距及具体位置等问题。由此将Sm2Co17的3个Co-Co哑铃对中的1个替换成Sm原子,即可得到SmCo7超胞。按照这种思路,构建了SmCo7的晶体结构,如图1b所示。此结构在原子比例上恰好为Sm∶Co = 1∶7,同时具有SmCo5的结构特性和Co-Co哑铃对的准确占比。在替换哑铃对的选择上,依据头对头不替换的原则,虚线圆圈位置的Co-Co哑铃对替换为Sm,模型更为合理。
图1 Sm2Co17 R相转变为SmCo7的晶体结构示意图
Fig.1 Schematics for the transition of crystal structure from Sm2Co17 R phase (a) to SmCo7 (b)
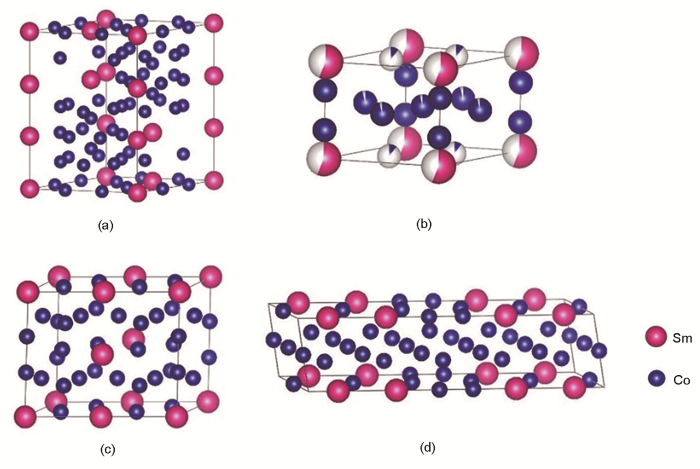
将建立的SmCo7模型与文献[17,23,24]中已有的3种SmCo7近似模型进行对比,如图2a~d所示。图2a为本工作新建立的SmCo7模型,共56个原子,包含7个Sm原子,49个Co原子,其中18个Co原子占据2c晶位,4个Co原子占2e晶位,27个Co原子占3g晶位,2e晶位的Co-Co哑铃对占比为2/9。图2b为SmCo8.5模型[23],共38个原子,包含4个Sm原子和34个Co原子,其中2e晶位的Co原子有4个,2c晶位的Co原子有12个,3g晶位的Co有18个,Co-Co哑铃对占比为2/6。图2c为SmCo7.3模型[17],一共有25个原子,包含3个Sm原子和22个Co原子,其中2e位置的Co原子有2个,Co-Co哑铃对占比为2/8。图2d为SmCo6.75模型[24],共有31个原子,其中Sm原子有4个,Co的3g位置原子有15个,Co的2c位置原子有10个,Co的2e晶位的原子有2个,Co-Co哑铃对占比为2/10。比较分析可见,只有SmCo7模型在原子比例上准确满足Sm∶Co为1∶7,且保持本征的CaCu5结构特性,Co-Co哑铃对占比准确。因此,本工作建立的模型确定为第一性原理计算SmCo7体系的最佳结构模型。
图2 SmCo7超晶胞结构及与文献[17,23,24]报道的SmCo7近似结构模型示意图
Fig.2 Schematics of crystal structure models of SmCo7 supercell in present work (a), and SmCo8.5[17] (b), SmCo7.3[23] (c), and SmCo6.75[24] (d) supercells in Refs.[17,23,24]
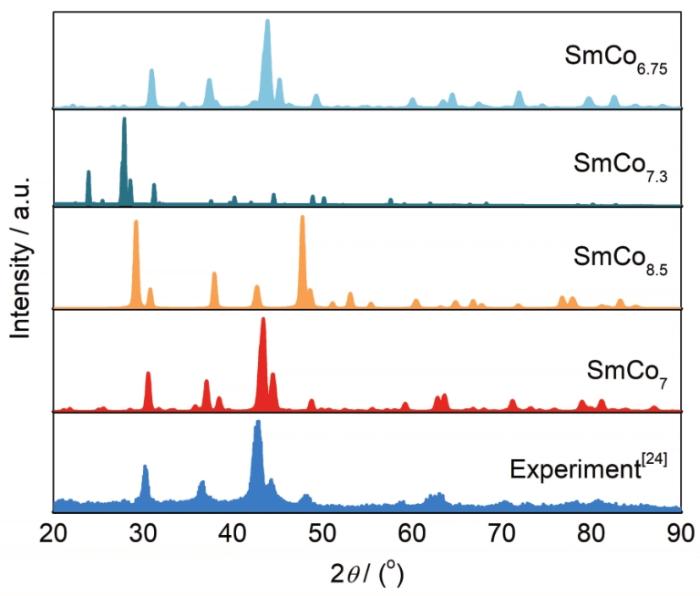
利用Materials Stuido中集成的Reflex模块对1.1节中4种SmCo7结构模型进行物相衍射模拟分析,结果如图3所示。SmCo8.5和SmCo7.3 2种结构模型的XRD峰值与实验峰值[24]偏差很大,表明这2种结构难以代表SmCo7的真实结构特性。SmCo6.75和SmCo7结构模型的XRD谱与实验结果[24]相近,仅在30°~40°之间存在1个杂相的峰。综合分析可知,本工作采用2/9的Co-Co哑铃对取代比例构建的结构模型与实验结果吻合良好,证明了SmCo7结构模型建立的合理性。
图3 4种SmCo7晶体结构模型对应的XRD模拟结果与实验结果[24]的比较
Fig.3 Comparison for the simulated XRD peak positions among the four SmCo7 structure models and the experimental result[24]
本工作计算Mn和In 2种元素单掺杂的SmCo7体系,构建掺杂模型时采用1.1节中建立的SmCo7的7倍超胞为基体,折合SmCo7单胞的晶格常数为:a = b = 0.4888 nm,c = 0.4107 nm,c / a = 0.840。考虑Mn和In 2种元素在Co中的溶解度,将各模型中的掺杂元素M的浓度设为2% (原子分数,下同),同时考虑M原子可能优先占据Co原子的3种不同晶位。首先建立Mn掺杂的1组模型,分别为未掺杂SmCo7超胞,Mn分别占据2c、2e和3g晶位的结构模型。
根据本研究组在In掺杂SmCo7实验方面的工作结果可知,In原子在Sm-Co体系中的作用比较复杂。尤其在亚稳相SmCo7基体中,当In原子添加浓度在1%~2%时,除主相SmCo7外,还存在SmCo5和Sm2Co17 2种杂相,当In的浓度超过2%,还会生成新的杂相Sm2Co9In3。在不考虑高掺杂量生成Sm2Co9In3的情况下,本工作研究In在Sm-Co混合相中的作用机制,分别建立In掺杂SmCo5、SmCo7和Sm2Co17超胞的一系列模型进行计算。为了方便对比分析,将SmCo5单胞扩大为9倍超胞,同时考虑In在3种Sm-Co基体可能占据不同位点的Co原子,建立一系列的模型。
本研究所有的计算都采用基于密度泛函理论的VASP软件进行计算[25,26]。泛函形式采取GGA-PBE方法[27,28]。进行结构几何优化时,平面波截断能设置为450 eV,原子的自洽总能量差和收敛准则分别设为10-4 eV和0.1 eV/nm,选用K点设置为3 × 3 × 2。计算时各原子的电子组态分别为:Sm-5s25p66s2、Co-3d74s2、Mn-3d54s2、In-4d105s25p1。本研究中重点关注元素掺杂对SmCo7结构稳定性和磁矩的影响,而Sm-Co原子间的4f-3d相互作用主要影响Sm-Co体系的磁晶各向异性能大小,因此可将4f电子视为芯内电子处理,即选用Sm-3赝势进行计算。
首先,对构建的SmCo7模型进行几何结构优化,使建立的晶胞处于体系能量最稳定的状态;随后用Mn和In在不同位点替代Co原子,并对得到的晶胞按照相同的计算参数进行几何结构优化,并在此优化基础上,通过引入电子自旋,进一步完善结构优化。实验研究得到的SmCo5晶格参数为a = b =0.4987 nm,c = 0.3981 nm,c / a = 0.798[29];计算得到的晶格参数为a = b = 0.4978 nm,c = 0.3951 nm,c / a = 0.793 (折合成SmCo5单胞)。SmCo7计算得到的晶格参数为a = b = 0.4863 nm,c = 0.4029 nm,c / a = 0.828,实验值为a = b = 0.4936 nm,c = 0.4007 nm,c / a = 0.812[15]。如表1所示,计算得出的SmCo5和SmCo7的晶格参数与实验值差异小于2%,说明建立的SmCo7模型合理,并且计算方法可靠。对比二元SmCo5和SmCo7单胞晶格参数发现,当引入Co-Co哑铃对后,体系的a减小,c增大,c / a有所增加。
表1 SmCo5和SmCo7超胞几何优化前后的晶格参数与实验值[15,29]对比
Table 1
为研究体系的物相稳定性及元素掺杂的难易程度,计算了初始体系和掺杂SmCo6.8M0.2体系的形成能Eform,可描述为[30]:
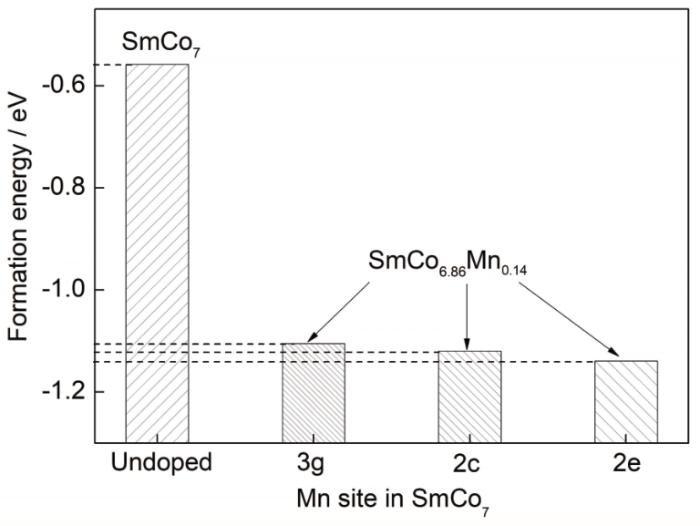
式中,E(total)为掺杂体系的总能量,n1、n2和n3分别为对应元素的原子个数,E(Sm)、E(Co)和E(M)分别是Sm、Co和M元胞的总能量。形成能为正值表示该元素掺杂较难,且体系物相稳定性较弱,反之,负值则表示元素较易于掺杂,且可增强体系的物相稳定性。对Mn元素掺杂前后的各体系形成能进行计算,结果如图4所示。未掺杂的二元SmCo7合金的形成能为负值,但趋近于0,说明其结构稳定性不高。Mn元素的引入降低了亚稳相SmCo7合金的形成能,使SmCo7的稳定性有所增加。对比Mn取代不同晶位Co原子的SmCo6.86Mn0.14体系形成能,可知Mn在SmCo7基体中优先占位排序为:优先占据2e晶位,其次为2c晶位,最后为3g晶位。由于Mn占据3种不同晶位时的形成能差值较小,Mn元素的添加超过一定量时,易发生占位的转变。
图4 掺杂元素Mn在SmCo7体系中3g、2c和2e晶位的形成能计算结果
Fig.4 Calculated formation energies of doping element Mn at 3g, 2c, and 2e sites in SmCo7 and that of undoped alloy for comparison
根据2.2.1节分析得知,同一种掺杂元素在替代不同晶位上的Co原子时,体系的形成能存在一定的差值,说明掺杂元素的占位会对形成能产生影响。因此当掺杂元素的占位发生改变时,合金体系的晶体结构稳定性也会受到影响。这主要是由于SmCo7晶胞中的次晶格Co的3种占位具有不同的空间体积,同时处在不同的成键环境中。一般情况下,第一性原理计算的能量值是在0 K (-273℃)条件下获得的,而晶体中的体积、原子半径等因素,在实际中会受到温度的影响。当温度改变时,由于原子热振动及晶体内点阵缺陷平衡浓度发生变化,会使原子间的距离发生改变,这不但会引起原子半径的改变,还会改变不同占位下的空间环境,进而影响占据不同位点的概率以及体系的稳定性。因此,有必要研究温度变化对掺杂元素占位产生的影响,以进一步分析温度对体系形成能和稳定性的影响。考虑到SmCo7合金的适用温度,利用Maxwell-Boltzmann分布定律[31],在0~900℃范围内对其掺杂元素的占位概率(Pi)进行研究。
式中,gi为简并度,i为晶胞中不同占位下的组态,ΔGi、ΔHi和ΔSi分别为Gibbs自由能、焓与熵的变化,Ef为通过第一性原理计算得到的形成能,P为压力,ΔV为晶胞体积变化,T为温度,kB为Boltzmann常数。熵变包括组态熵与振动熵2部分,每个原子的振动熵平均为0.1kB~0.2kB,组态熵(S)取决于置换晶位的数目和掺杂量的大小[32,33],可描述为[34]:
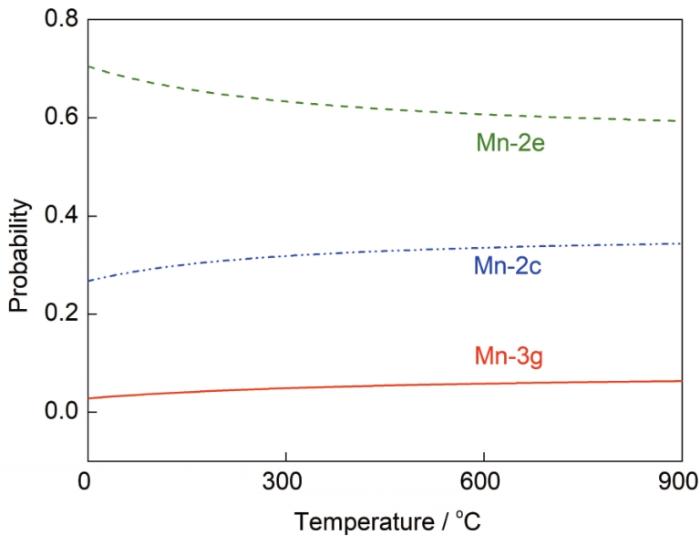
式中,Ω为组态数。由于掺杂元素引起的体积变化很小,因此采用近似处理PΔV = 0[35]。所以利用第一性原理计算得到的形成能,结合统计热力学Maxwell-Boltzmann分布,即可预测SmCo6.86Mn0.14体系在较高温度下的结构稳定性。在较宽的温度范围(0~900℃)内,SmCo7合金中Mn的掺杂位点占位概率随温度的变化关系如图5所示。Mn占据Co-2e晶位的概率始终相对最高,其次是Co-2c晶位,占据3g晶位的概率趋近于0。从Maxwell-Boltzmann方程来看,影响概率的主要因素是体系能量,由于2e 晶位的取代能远小于另外2种晶位,因此2e晶位的占位概率和稳定性最高。随着温度的升高,Mn占据Co-3g晶位的概率未发生明显改变,说明Mn占据此晶位的概率始终较低。而2e晶位的占位概率缓慢降低,2c晶位的占位概率随温度逐渐升高。图5的结果表明,Mn在SmCo7中的占位概率受温度影响不显著,Mn掺杂适用的温度范围较广。
图5 SmCo6.86Mn0.14体系中Mn在不同位点的占位概率随温度的变化
Fig.5 The calculated site occupation probability of Mn as a function of temperature for SmCo6.86Mn0.14
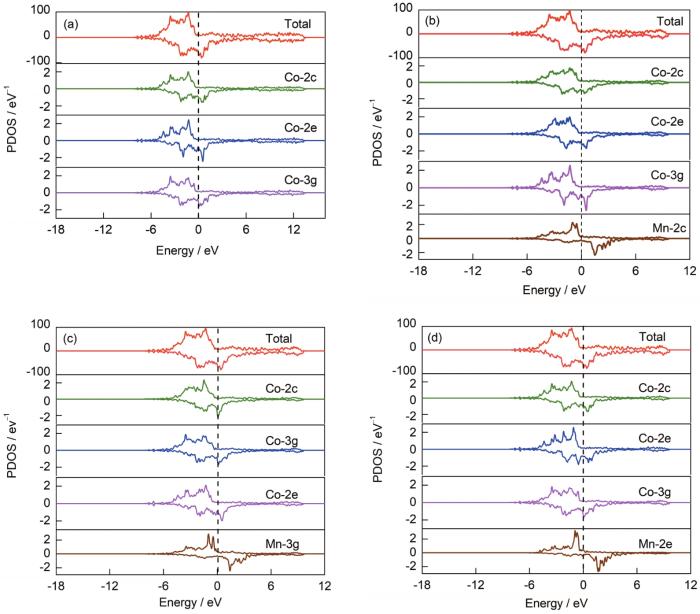
为阐明Mn添加对SmCo6.86Mn0.14体系稳定性影响的微观机理,对Mn掺杂前后体系的偏态密度进行了计算,以此分析元素掺杂对体系电子结构的影响。体系的总态密度、Mn原子和不同位点的Co原子的偏态密度如图6所示。
图6 Mn掺杂前后各体系的总态密度(DOS)及各原子的偏态密度(PDOS)
(a) SmCo7 (b) SmCo6.86Mn0.14 (2c)
(c) SmCo6.86Mn0.14 (3g) (d) SmCo6.86Mn0.14 (2e)
Fig.6 Total density of states (DOSs) and partial density of states (PDOSs) of elements in undoped and Mn doped systems
对比Mn掺杂前后各体系总态密度图可知,添加Mn后体系总态密度峰值降低,这是由于Mn的电子数目比Co少,使态密度峰值降低,离域性增强,说明体系的稳定性升高。如图6b~d所示,在Fermi能级附近,Mn自旋向上峰值与不同位点的Co均具有峰型共振的现象,说明Mn与Co之间具有较强的相互作用。Mn占据不同位点时,其周围Co原子偏态密度峰值明显不同,当Mn占据2c位时,Co-3g偏态密度峰值明显增高,Co-2c和Co-2e偏态密度峰值降低;当Mn占据3g位时,Co-2c偏态密度峰值略微增高,Co-3g和Co-2e偏态密度峰值下降;当Mn占据2e位时,周围的Co-2c和Co-3g偏态密度变化较小,而Co-2e偏态密度在掺杂前后变化最为明显,说明Mn-Co(2e)间相互作用最强,在增强体系稳定性的过程中起到主要作用,这与对体系形成能计算得到的Mn优先占据Co-2e晶位的结果相一致。
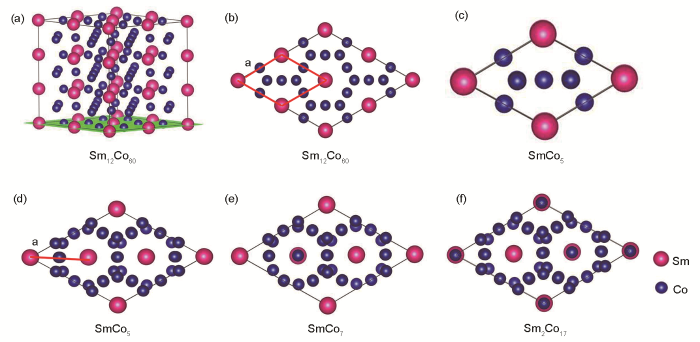
实验表明In元素掺杂亚稳相SmCo7会产生SmCo5、SmCo7和Sm2Co17 3相共存的混合物。由于计算得到的晶胞参数属于超胞体系,3种物相的超胞大小不同,因此要研究In添加对SmCo5、SmCo7和Sm2Co17晶胞变化的影响,需要将3种超胞折合成SmCo5单胞大小。如图7所示,图7a是12倍SmCo5 (1 × 3 × 4)的超胞结构图,图7b和c分别是12倍的SmCo5超胞和SmCo5单胞在(001)面的投影图。图7d是由Sm2Co17中的3个Co-Co哑铃对全部替换成Sm原子后形成的9倍SmCo5体系。如图7d~f所示,通过各结构模型在(001)面的投影分析,可以看出12倍SmCo5 (1 × 3 × 4)的超胞旋转60°后可得到与SmCo5、SmCo7和Sm2Co17 3种结构相似的原子排布。在12倍SmCo5 (1 × 3 × 4)的超胞中折合成单胞的晶格常数a为红色线段部分,即为计算得到的a和晶格常数b的1/4、晶格常数c的1/3,此时获得的晶格常数与SmCo5单胞的相同。
图7 Sm12Co60超晶胞结构及SmCo5、SmCo7和Sm2Co17模型在(001)平面投影示意图
(a) Sm12Co60 supercell supercell structure
(b) Sm12Co60 supercell supercell (Supercell structure model projected on the (001) plane)(c) SmCo5 unit cell (d) SmCo5 supercell
(e) SmCo7 supercell (f) Sm2Co17 supercell
Fig.7 Diagram of Sm12Co60 supercell structureand the models of SmCo5, SmCo7, and Sm2Co17 projected on the (001) plane
考虑In在SmCo5中有2种可能占位,在SmCo7中有3种可能占位,在Sm2Co17中有4种可能占位,同时建立不同占位的结构模型,加上未掺杂模型共计12个模型,如表2所示,A、B和C分别为优化后的SmCo5、SmCo7和Sm2Co17模型,不同数字代表掺杂元素占据不同位点。对比未掺杂的3个模型的体积,可以看出,SmCo5的体积最大,Sm2Co17最小,这是由于Sm原子半径较大,Sm被Co-Co哑铃对替换后,引起体积收缩。由于In原子半径较大,3类模型的体积均随In的掺入而增大,使得掺杂体系的晶胞发生畸变,进而影响体系的稳定性。
表2 计算的In掺杂SmCo5、SmCo7和Sm2Co17前后的晶格参数和晶胞体积
Table 2
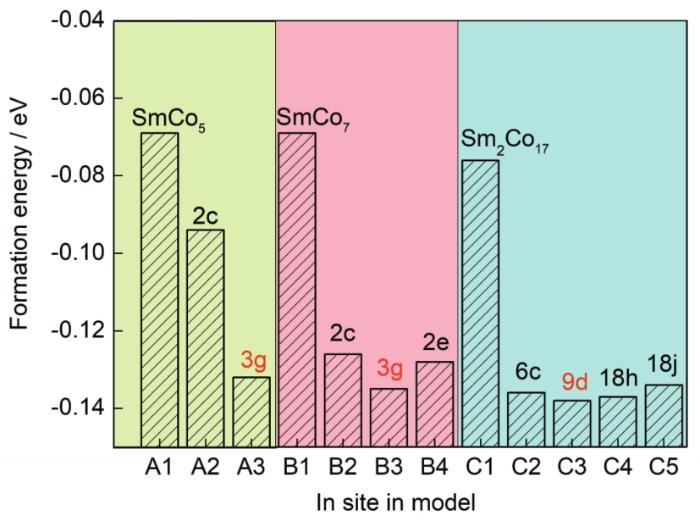
为了研究In的择优占位规律,对掺杂前后的各体系形成能进行了计算,结果如图8所示。Al、B1和C1代表未掺杂体系,其形成能均为负值,但都趋近于0,说明3种基体稳定性较低,易发生相分解,其中Sm2Co17形成能最低,SmCo7最高,这与SmCo7是亚稳相的实验事实相符。比较In掺杂各体系的形成能,可知In在SmCo5基体中,优先占据3g晶位,在SmCo7中优先占据3g晶位,而在Sm2Co17中,优先占据9d晶位。当3种相共存时,In更倾向于优先进入Sm2Co17相中。
图8 In掺杂的SmCo5、SmCo7和Sm2Co17体系中In原子占据不同晶位的形成能计算结果
Fig.8 Calculated formation energies of SmCo5, SmCo7, and Sm2Co17 systems with doped In at different sites and those of undoped systems for comparison
为进一步考察In掺杂Sm-Co体系在不同温度下的占位概率变化特点,利用第一性原理计算得到的形成能,结合统计热力学Maxwell-Boltzmann分布进行计算,结果如图9所示。图9a是In在SmCo5体系中Co的2c和3g晶位上的占位概率与温度之间的关系。从图中可以看到,In优先占据3g晶位,随着温度的升高,2种晶位的占位概率发生改变,3g晶位的占位概率略有下降,同时占据2c晶位的概率稍有增加。当占据不同位点的形成能差值较小时,位点的几何环境相似,掺杂元素易发生占位的转变。如图9b所示,随着温度的升高,In占据3g位点概率降低,占据2e位点的概率增大,占据2个不同位点的概率具有相交的趋势。在Sm2Co17中也具有相似的规律,如图9c所示,随着温度的升高,In在9d晶位的占位概率出现明显下降趋势,而其他3种占位的概率则同时出现升高的现象。对比In在3种体系中的占位概率随温度的变化规律可知,在SmCo5中In不容易发生占位转变,这与图8所示的在SmCo5中占据不同位点的形成能差值较大相吻合。而在SmCo7中In最易发生占位的转变,这也表明,SmCo7基掺杂体系的结构稳定性受温度影响较大。
图9 掺杂元素In在不同体系中的占位概率随温度的变化
(a) SmCo5 (b) SmCo7 (c) Sm2Co17
Fig.9 Variations of occupation probability of In doping with temperature in different systems
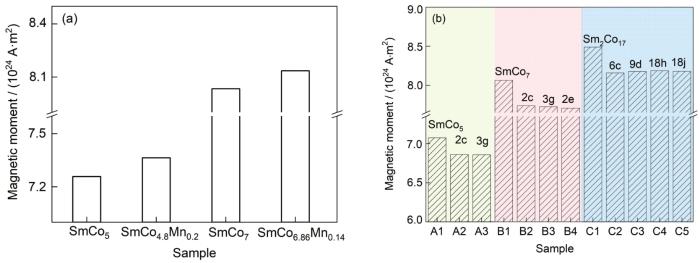
掺杂Mn前后SmCo5和SmCo7体系的磁矩变化如图10a所示。在SmCo7体系中掺杂Mn元素,体系总磁矩出现升高的现象,与文献[21]中添加Mn可使SmCo5体系总磁矩升高的结论一致,说明Mn元素有利于提高Sm-Co体系合金的饱和磁化强度。在SmCo5和SmCo7超胞中分别添加1个Mn原子后,总磁矩增加的大小相似,Mn的原子磁矩大小对体系总磁矩影响明显。
图10 掺杂Mn和In前后的SmCo5、SmCo7 和Sm2Co17超胞总磁矩
(a) SmCo5 and SmCo7 supercells with or without Mn doping
(b) SmCo5, SmCo7, and Sm2Co17 supercells with or without In doping at different sites
Fig.10 Total magnetic moments of SmCo5, SmCo7, and Sm2Co17 systems doped Mn and In at different sites and undoped systems
对In掺杂SmCo5、SmCo7和Sm2Co17体系不同占位的各结构模型的总磁矩进行计算,结果如图10b所示。在未掺杂体系中总磁矩由大到小的顺序为Sm2Co17 > SmCo7 > SmCo5,这是由于Sm-Co体系磁性主要来源于Co次晶格,体系中Co原子占比越大,体系总磁矩越大,因此Sm2Co17合金的饱和磁化强度最高。随着In元素的引入,SmCo5、SmCo7和Sm2Co17体系的总磁矩均有所降低,一方面是因为非磁性元素In替代磁性元素Co会造成一部分磁矩的损失;另一方面,In会影响其周围Co原子的磁矩,使其被削弱。但由于In原子半径较大,使周围Co-Co原子间距减小,从而提高部分次近邻处Co原子的磁矩,对总磁矩的减小起到补偿作用。因此相比于绝大多数元素添加后均明显降低Sm-Co体系的饱和磁化强度而言,In的添加对于Sm-Co体系的饱和磁化强度降低程度较小,In可以被认为是对Sm-Co体系饱和磁化强度的友好型掺杂元素。
(1) 通过分析Sm-Co基二元合金结构转变规律,采用Sm2Co17相中的Co-Co哑铃对逆向替换Sm的方法,成功构建了Sm∶Co原子比例恰好为1∶7的晶体结构模型,突破了长久以来没有精准Co-Co哑铃对占比且适用于第一性原理计算的SmCo7结构模型的难题,并通过计算验证了模型的合理性。
(2) 掺杂浓度为2% (原子分数)的Mn元素可降低SmCo7亚稳相的形成能,提升SmCo7的稳定性;对于不同温度下占位概率的计算表明,Mn的占位概率随温度升高变化不明显,因此掺杂Mn可在较宽温度范围内使用;电子结构分析可知,Mn-Co间存在较强的相互作用,有利于提升体系的稳定性。
(3) 添加浓度为2%的In,SmCo7体系中存在SmCo5、SmCo7和Sm2Co17 3种相,In优先占据Sm2Co17的9d晶位。添加少量In可使Sm-Co体系的形成能降低,从而提高SmCo5、SmCo7 和Sm2Co17相的结构稳定性。
(4) 添加反铁磁元素Mn有利于提高SmCo7体系的总磁矩,促使饱和磁化强度升高;而添加元素In使SmCo5、SmCo7和Sm2Co17体系总磁矩均降低,但是降低程度较小。添加相同原子个数的In引起不同Sm-Co体系的净磁矩减小程度相似。
1 模型构建与计算方法
1.1 模型构建
图1
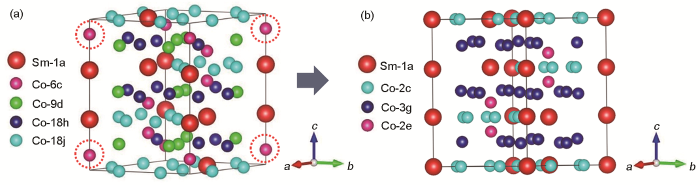
图2
1.2 模型合理性验证
图3
1.3 掺杂模型建立
1.4 计算方法
2 计算结果分析
2.1 SmCo7计算结果分析
Model
Lattice parameter / nm
c / a
a
b
c
SmCo5
0.4978
0.4978
0.3951
0.793
Experiment[29]
0.4987
0.4987
0.3981
0.798
SmCo7
0.4863
0.4863
0.4029
0.828
Experiment[15]
0.4936
0.4936
0.4007
0.812
2.2 Mn掺杂对SmCo7稳定性的影响
2.2.1 稳定性及择优占位
图4
2.2.2 温度对择优占位的影响
图5
2.2.3 电子结构分析
图6
2.3 In掺杂对SmCo7结构稳定性的影响
2.3.1 稳定性及择优占位
图7
Number
Model
a / nm
c / nm
c / a
V / nm3
A1
SmCo5 (9 supercell)
0.4968
0.3943
0.790
0.759
A2
Sm9Co44In (2c)
0.4900
0.3962
0.808
0.772
A3
Sm9Co44In (3g)
0.4928
0.3958
0.803
0.773
B1
SmCo7
0.4863
0.4029
0.828
0.741
B2
Sm7Co48In (2c)
0.4224
0.4054
0.959
0.754
B3
Sm7Co48In (3g)
0.4226
0.4039
0.956
0.754
B4
Sm7Co48In (2e)
0.4233
0.4038
0.954
0.752
C1
Sm2Co17
0.4821
0.4046
0.840
0.731
C2
Sm6Co50In (6c)
0.4195
0.4063
0.968
0.743
C3
Sm6Co50In (9d)
0.4198
0.4062
0.967
0.745
C4
Sm6Co50In (18h)
0.4199
0.4062
0.967
0.745
C5
Sm6Co50In (18j)
0.4196
0.4075
0.971
0.745
图8
2.3.2 温度对In掺杂择优占位的影响
图9

2.4 Mn和In单掺杂对SmCo7磁矩的影响
图10
3 结论
来源--金属学报







 沪公网安备31011202020290号
沪公网安备31011202020290号
